超长水平井连续管下入深度优化及验证

刘研言 尹俊禄 慕 鑫 王宝宏

中国石油川庆钻探工程有限公司长庆井下技术作业公司

0 引言

随着油气田资源不断深入的勘探和开发，水平井在薄储层、边际气藏、枯竭气藏、稠油藏的开发上展现出明显优势，超深、超长水平井的出现需要更多的连续管施工[1-2]。但是，由于水平井井眼轨迹的曲率和方位变化，连续管作业时会遇到更大的阻力，连续管的下入深度将受到严重影响，直接导致施工效率降低，甚至无法达到作业深度[3]。

连续管具有带压作业和快速起下的优点，但因其质量轻、刚度低、挠度大、径向尺寸小等特点，在长水平井作业时，会与套管之间形成较大的环空间隙，受到井壁的约束，在轴向力作用下易在井筒内出现螺旋屈曲现象，尤其是超长水平井，往往难以下入至预期作业深度[4-6]。国内外学者研究[7-13]发现，随着连续管下入水平段长度的增加，其与套管壁的摩擦阻力也相应增加，随之产生屈曲变形。当载荷进一步增大，管柱从正弦屈曲逐步转变为螺旋屈曲进而转变为螺旋自锁。一旦管柱发生自锁现象，轴向载荷将不能有效传递，这已经成为制约连续管施工工艺措施的关键因素。

针对这一问题，国内外学者均开展了相应的研究[14-20]，从井身结构设计方面来优化井眼轨迹，实现减阻降摩的目的，从作业连续管的规格上提高刚性，从减少摩擦力等诸多方面都做了大量的研究。笔者系统地分析了影响顺利下入施工的主要原因，基于减摩减阻的原理，提出连续管水平井下入深度的优化方法。

1 连续管受力模型及算法体系的建立

根据经典管柱力学，笔者分析在下入、上提时作用在连续管上的载荷和应力大小分布。分析时考虑浮力、摩擦阻力、工作管柱和工具串重量、井口压力等对各种预测作业参数的影响。这些作业参数包括悬重、螺旋屈—曲极限和自锁点。

1.1 连续管管柱受力模型

管柱载荷计算方面提出的计算模型有2种，即软绳模型、刚杆模型。各模型的计算能力如表1所示。

表1 不同模型计算能力对比表

管柱载荷计算的2个模型中，软绳模型计算最为简单，计算规模最小，尤其适用于各种直井段和井眼曲率变化较小的油井。软绳模型没有考虑管柱的刚度，忽略了管柱所受的弯矩，在复杂井眼情况下，其计算精度较差。但在井眼轨迹变化较小、管柱单元段划分较细致情况下，其计算结果还是具有很高可靠性的。所以，即使该模型有一些不足，但应用比较广泛。

刚杆模型是在软绳模型基础上发展起来的，充分的考虑了管柱材料、刚度和井眼轨迹影响，并在力学模型中引入了弯矩方程，所以其计算能力比软绳模型大为提高，尤其适用于井眼曲率变化较大的井况。但对于井眼曲率变化较小的井段，一般不建议采用，因为它将导致结果难于收敛。此外，由于增加了弯矩计算，计算过程中需要求解一个比较复杂的方程组，计算规模比软绳模型大为增加，但仍然在可接受的范围之内。所以，刚杆模型的应用也比较广泛。

1.2 连续管管柱受力算法

针对井段结构的不同，将连续管分为垂直段、造斜段与水平段，具体分段结构如图1所示。利用上述管柱受力计算模型，对连续管进行分段受力情况分析计算[21]，在连续管垂直段中，自重的作用使得管壁与井壁之间接触面积较小，不会产生明显的摩擦阻力，因此轴向力连续管在井眼中浮重的影响，呈线性变化，变化趋势如图2所示。

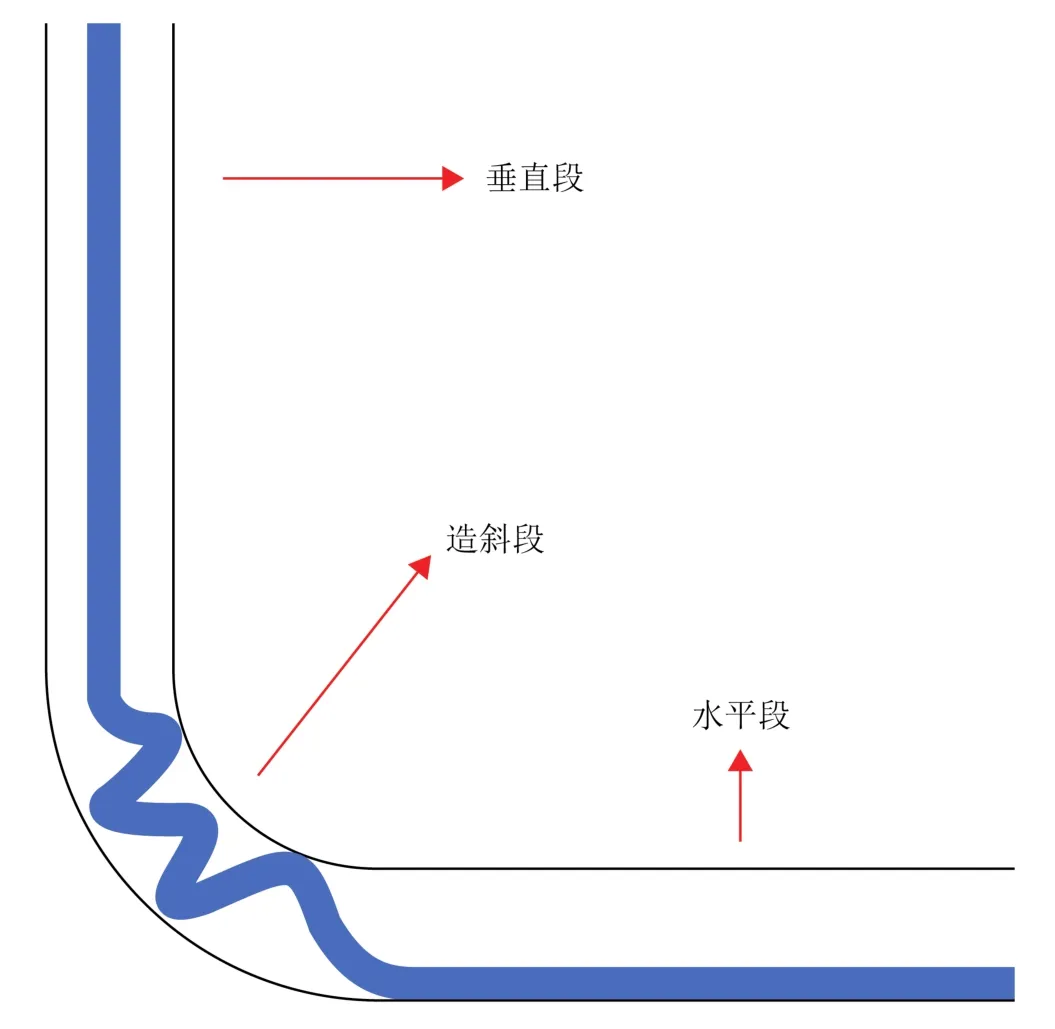
图1 连续管分段结构示意图

图2 垂直段连续管轴向力分布示意图

其中，任意井深z处连续管轴向载荷为：

式中F0表示连续管在z=0处的轴向载荷，N；W表示连续管在井眼中的浮重，N。

连续管在井内下放过程中，受摩阻力影响，易发生屈曲变形，当连续管受到的轴向力达到连续管正弦屈曲临界载荷时，连续管发生正弦屈曲。

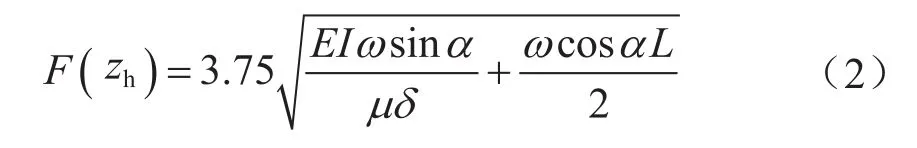
式中zh表示连续管发生正弦屈曲时在井眼中的坐标，m；E表示连续管弹性模量，MPa；I表示连续管惯性矩，m4；α表示连续管井斜角，（°）；ω表示单位长度连续管自重，kN；μ表示连续管与井壁的摩擦系数；δ表示管柱与井眼之间的径向间隙，mm。

随着连续管受到的轴向力逐渐增加，当达到螺旋屈曲临界载荷后，连续管将无法继续传递轴向力，发生“锁死”现象，这时到达连续管下入的极限深度。

式中zb表示连续管发生螺旋屈曲时在井眼中的坐标，m。

根据式(3)即可计算连续管下放的极限深度。

2 连续管下入深度影响因素分析与计算

2.1 因果链影响因素分析法

根据因果链分析方法来分析连续管下入深度影响因素。因果链分析是全面识别工程系统缺点的分析工具。因果链分析，始于项目目标决定的初始缺点，分析其影响因素，得出中间缺点，并进而继续挖掘下一层级的影响因素，直到末端缺点。表2为通过因果链分析法得出的连续管下入影响因素汇总分类分析表。

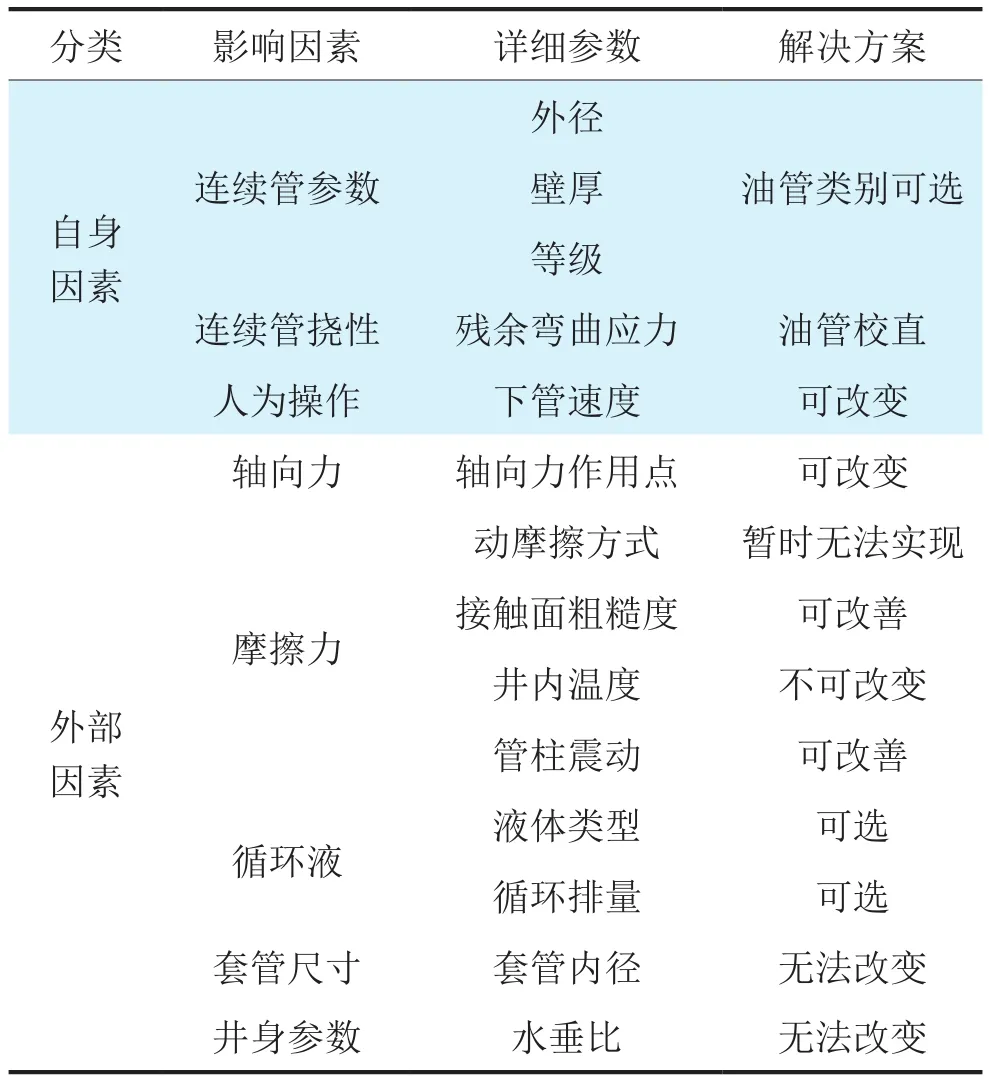
表2 连续管下入影响因素汇总分类分析表

从表2中可以发现，影响连续管下入深度的因素存在自身因素和外部因素，自身因素中的连续油管参数可以进行调整，外部因素主要是轴向力和摩擦力其他影响因素的可控性和改善后的收益预估较低，暂不考虑。笔者将针对连续管参数、轴向力以及摩擦力进行数值计算。考虑到投入成本和工程量的问题，在选择最佳参数管柱后，针对轴向力和摩擦力进行现场试验验证。

2.2 下入深度影响因素计算

通过连续管下入影响因素的分类，目前克服影响因素可行的方案为针对连续管自身因素优选最佳参数管柱，外部因素为降低摩擦作用或者增加轴向牵引力。根据公式（3），改变式中对应的弹性模量、惯性矩和摩擦系数，对以上3种影响因素进行计算分析，分析过程如下。

2.2.1 连续管自身参数

连续管入井后形变和轨迹受连续管自身参数影响，这些参数主要包括连续管管径和连续管壁厚。与此同时，连续管在套管内运移，同样受套管尺寸制约，为了排除套管尺寸对连续管下深的影响，此处先考虑套管尺寸的影响效果，而后再对连续管管径以及壁厚进行计算和分析。模拟计算井筒状态如下：井眼套管采用Ø139.7 mm×9.17 mm、P 110钢级，连续管工作介质（清水）密度为0.988×103kg/m3，设造斜段的造斜率为6°/30 m，连续管与套管之间的摩擦系数μ取0.3。

图3给出了不同管径下套管尺寸与下入深度的关系。从图中可以发现，随着套管尺寸的增加，下入深度呈现先增加后降低的趋势；同时，连续管的管径越大，下入深度越大。套管尺寸的变化，不会影响管径对下深的变化趋势，因此后续计算将选择Ø114.3 mm套管尺寸来进行计算。

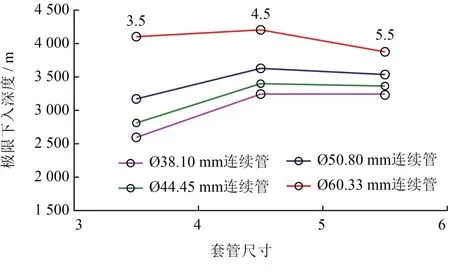
图3 改变套管尺寸的计算结果示意图

图4给出了不同管径下连续管壁厚与下入深度的关系。从图中可以发现，随着连续管壁厚的增加，下入深度逐渐降低。随着连续管管径的增加，壁厚对下入深度的影响趋势基本保持不变。壁厚对下入深度的影响要小于连续管管径对下入深度的影响。

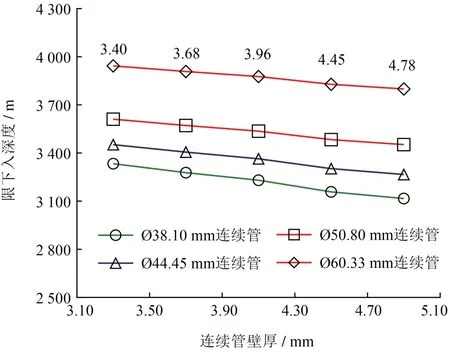
图4 改变连续管壁厚的计算结果示意图

结合图3和图4可以发现，管径越大，下入深度越大，这是由于连续管管径越大，其挠度越低，产生缠绕和自锁的条件越难，因而可以使下入深度更大。

2.2.2 轴向牵引力

力的三要素为作用点，方向和大小。在连续管下入井筒，需要注入头不断提供加载动力，特别是进入水平段后，连续管与井筒之间的摩阻增大，连续管在井筒内发生屈曲变形，随着摩擦阻力的进一步增大，从井口增加的任何推力都会被摩擦而抵消，使得管柱无法继续下入，从而发生螺旋锁定。若改变力的作用点，在管端增加新的牵引力，使得整个连续管下入变为牵引器拉，注入头推，从而有效增加连续管在水平段的延伸。

计算结果由图5可得，在管端仅增加100 kg牵引动力就可以增加38.1 mm连续管多延伸108 m，在100 kg至1 000 kg附加牵引力下，4种规格Ø38.10 mm，Ø44.45 mm，Ø50.80 mm，Ø60.33 mm连续管在水平段的最大深度均有提高。

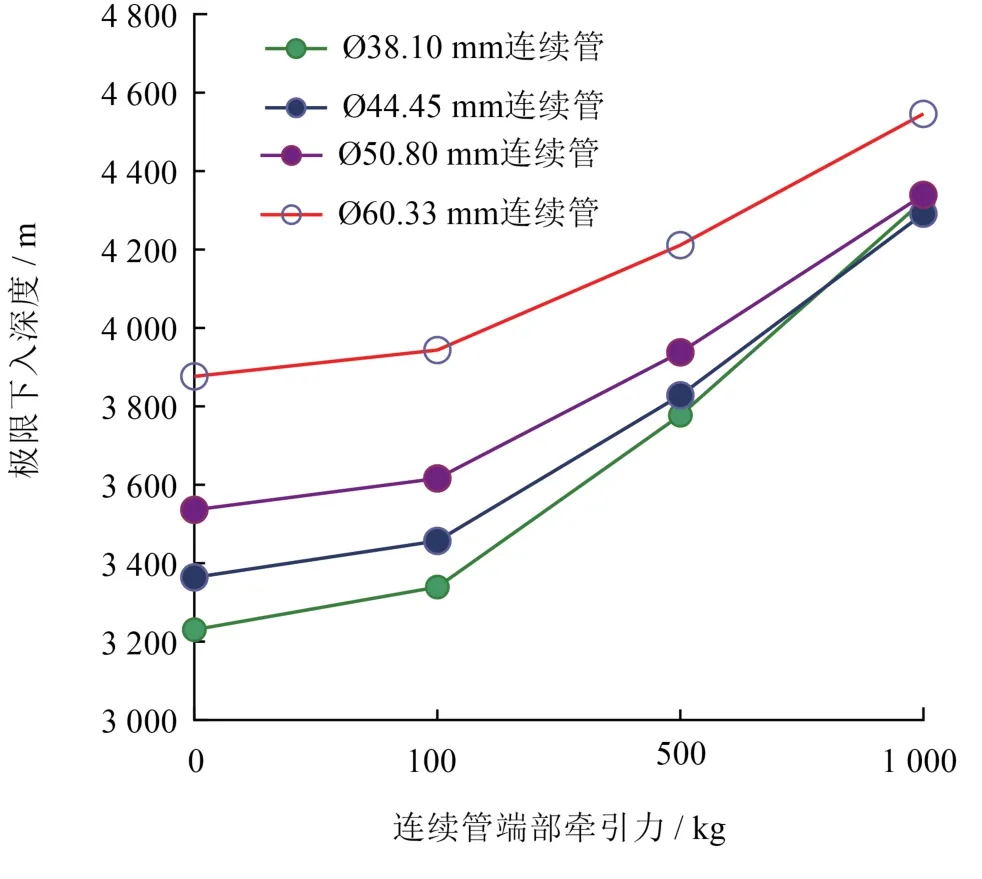
图5 增加管端牵引力的计算结果示意图

对比两种下入方式发现Ø38.1 mm的连续管在附加牵引力作用下的下入深度提升最大。牵引力增加的下深顺序依次为Ø38.10 mm＞Ø44.50 mm＞Ø50.80 mm＞Ø60.30 mm。提供附加牵引力后，4种规格连续管的极限下入深度增加深度发生反转，其原因主要是未提供附加牵引力时，相同壁厚管柱的外径越大，下入深度越大；提供附加牵引力后，外径越大的管柱由于与井眼之间接触反力越大，摩擦力越大，而外径较小的管柱由于摩擦力较小，因此能继续下入的深度较大，这种结果最终导致不同规格管柱在水平段增加下入深度的反向分布。当附加牵引力的大小被管柱与井壁之间的摩擦力消耗殆尽时，管柱达到极限下入深度。

2.2.3 摩擦系数

摩擦系数的变化可以由水力振荡器和金属降阻剂共同提供。水力振荡器通过改善井内管壁与井壁之间的摩擦条件，降低摩擦系数，将管壁的静摩擦状态改变为动摩擦状态，显著降低连续管的局部摩阻。金属降阻剂从本质来说是一种加入减摩添加剂的润滑剂，同时兼备润滑和减摩的作用。从润滑方面而言，它能减少连续管与井筒之间的摩擦和磨损，延长连续管的使用周期；从减摩方面而言，减摩添加剂与金属或金属氧化物具有很强的亲和力，容易被吸附或反应形成低抗剪强度的膜，阻止连续管与井筒之间的直接接触，从而降低摩擦系数。

图6给出了不同摩擦系数下下入深度的计算结果，从图中可以得知摩擦系数越大，下入深度越小。通过计算可知对于Ø38.10 mm，Ø44.50 mm，Ø50.80 mm，Ø60.33 mm连续管而言，管径越小，极限下入深度越大，且对于同样加入降阻剂来说，管径越大，金属减阻剂的减阻效果越明显。

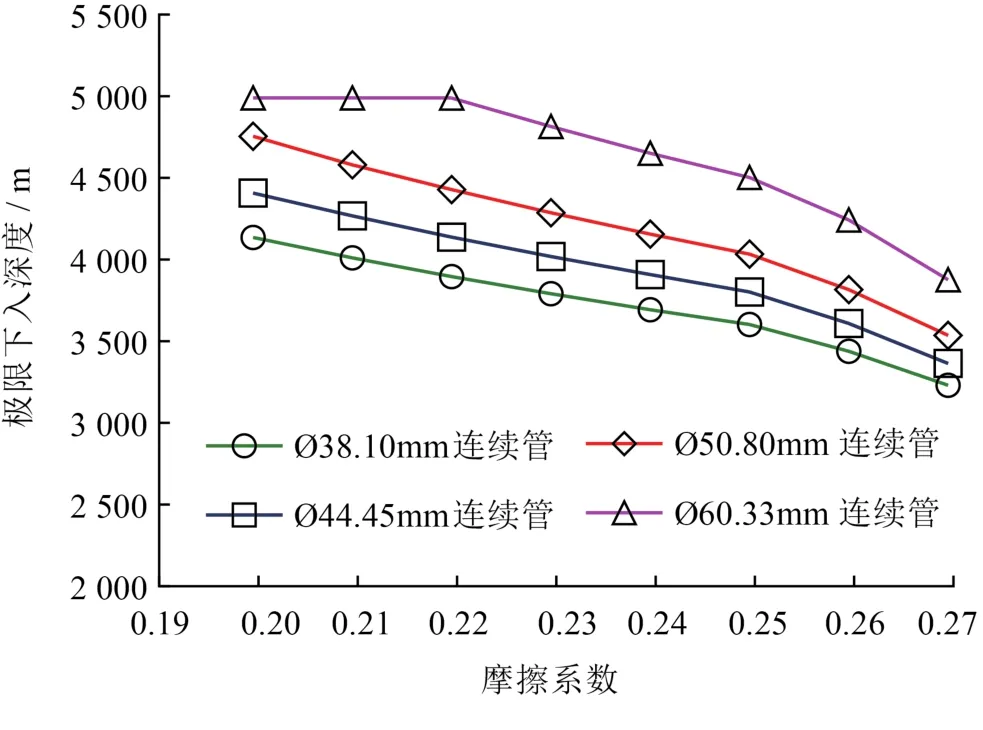
图6 不同摩擦系数的下深结果示意图

3 现场试验验证与分析

由于现场试验固定了连续管尺寸和材料，因此无法验证连续管自身参数的改变带来的效果。针对轴向牵引力和摩擦力，在现场使用水力振荡器来实现改变轴向牵引力产生的效果，使用不同的金属降阻剂来实现改变摩擦力产生的效果，对水力振荡器和金属降阻剂在现场试验的结果进行分析和对比，从而验证软件计算的可靠性并得出相应的结论。

笔者采用的现场数据为靖A井的基础数据，井身结构如图7所示。靖A井的人工井底为6 248.83 m，造斜点为2 560.00 m，入窗点为1 935.00 m，水平段长2 900.00 m，垂直井深为3 126.35 m。最大井斜90.65°，油层套管外径114.30 mm，壁厚7.37 mm，钢级P110。选用外径为50.80 mm，钢级为CT110，变壁厚连续管。

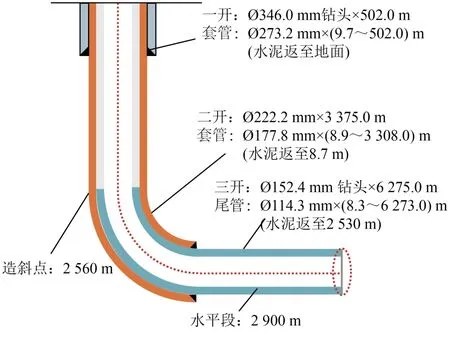
图7 靖A井井身结构示意图

3.1 现场测试关键工具

3.1.1 水力振荡器

水力振荡器主要通过产生轴向振动来减少钻具与井壁间的摩擦力。在现场测试中通过水力振荡器来提供连续管轴向牵引力。水力振荡器的技术参数如表3所示。

表3 水力振荡器技术参数展示表

3.1.2 金属减阻剂

连续油管由于自身的柔韧性，使其在井筒内易发生弯曲和摩擦锁定，导致不能下入到预定深度进行后续作业，在长水平段施工中尤为突出，基于此自主开发了用于增加连续管下入深度的金属减阻剂。对金属减阻剂配比进行室内试验得到的数据如表4所示：

表4 金属减阻剂室内试验结果统计表

从上表中可以看出，泵入5%金属减阻剂井筒摩擦系数达到最小值，故选用5%金属减阻剂添加配比。在现场测试中通过添加金属减阻剂的方式来降低摩擦系数。

3.2 现场测试实例

第1次入井不带水力振荡器，也不添加金属减阻剂，连续管下入4 556 m自锁。第2次入井带水力振荡器，并添加5%金属降阻剂，连续管下至6 245 m到达井底，水平段下深3 252 m。也就是在该井井眼轨迹下，Ø50.8 mm连续油管在金属降阻剂和水力振荡器共同作用下最长水平段下深3 252 m，整体下深较第1次入井增加了1 689 m。

图8为对全井段连续管悬重与深度进行回归分析的曲线图。图中下放深度3 000 m处为造斜点位置，从图中可以看出，连续管2次入井过程中在垂直段的载荷均为线性增长，这与上述公式分析互相印证。超过3 000 m之后，连续管轴向载荷开始逐渐减小，其中第1次入井载荷下降速率明显快与第2次入井的载荷下降速率。两次入井过程中，载荷锐减位置即为到达极限下入深度，第2次入井下深明显大于第1次入井的下深。由此可以发现，通过加入水力振荡器和添加金属减阻剂来降低摩擦系数，能够有效地提高连续管的下放深度。

图8 载荷深度回归曲线图

4 结论

1）通过因果链分析法得出影响连续管下入的主要因素为连续管在入井前残余弯曲应力，在井筒的限制和轴向力的作用下，在井筒内发生屈曲变形，产生自锁。

2）通过公式推导和理论计算可知，选择相对大尺寸、小壁厚的连续管可以延长一定的下入深度，但要大幅增加连续管的下入深度还要采用增加管端牵引力以及降低摩擦系数的方法。

3）在现场使用水力振荡器来实现改变轴向牵引力产生的效果，使用不同的金属降阻剂来实现改变摩擦力产生的效果，对试验结果进行分析和对比，确认这2种方式均能够显著降低摩擦系数，从而有效提高连续管的下放深度。