高中数学教学中体现数学文化的方法

□甘肃省岷县第一中学 李小东

在数学课堂中重视体现数学文化，能够让学生感受到数学独有的文化价值，而在数学文化的熏陶下，学生的数学素养会得到有效的培养和发展。同时，学生还能在学习中对数学知识产生兴趣和探究欲望，进而提高学习主动性，并获得良好的德育。在数学教学中体现出数学文化，是新课标中一项新的要求，而如何在课堂中体现数学文化，也成为教师急需探究的新任务。在高中数学教学中，教师可以通过介绍数学史、展示数学美、渗透数学思想等途径体现数学文化，构建高效且具有人文精神的数学课堂。但实际教学中，数学文化的体现仍存在一些问题，需要教师在课堂中不断探索和完善。本文就高中数学教学中如何体现数学文化展开分析，并提出几点策略。

一、数学文化渗透对学生的影响

数学文化中有着丰富的内涵，是数学学科发展过程中知识与人文的结合，在课堂中合理运用，能够让学生的思维受到熏陶，促使学生认识到数学文化的价值。同时，数学文化渗透对学生会产生多方面的影响。首先，学生的数学素养参差不齐，在课堂学习中学生更重视对数学知识的学习，忽视了对数学文化的探究。如果教师能够改变教学形式，将数学文化融入课堂教学中，这在丰富课堂内容的基础上，还能提高学生学习数学的兴趣，并促使学生在教师在指导下，体会到数学思想方法。其次，数学文化包括数学史、数学思想等多方面的内容，合理渗透在课堂中能够有效拓展学生的知识面。另外，教师在渗透数学文化时，还会融入知识形成或探究过程，这对学生深入了解和掌握知识点也有较大的帮助。最后，数学文化的渗透还，有助于激发学生的爱国热情，在了解和学习数学文化时，学生会对古代数学家、对数学的研究有一定的了解，间接感受到传统文化的魅力，从而更好地激发自己的爱国热情。综上可以看出，在数学课堂中合理渗透数学文化，能够有效拓宽学生的视野，增强学生应用数学的意识，对激发学生的爱国热情也有较大的帮助，教师要在课堂中选择恰当的时机引入数学文化。

二、高中数学教学中体现数学文化的途径

（一）挖掘教材，体现课本文化内涵

1.通过数学史渗透数学文化

为了体现数学文化的价值，也为了让学生认识到数学文化的重要性，当下部分高中数学教材中都加入了数学史相关的内容，介绍了数学领域的代表人物及对数学发展的贡献。教师在教学中可以合理运用史料来渗透数学文化，激发学生的学习兴趣。在教材内容的基础上，教师还可以借助网络搜集资料，完善其中的数学家故事，引导学生认识到数学家们不怕困难的科学精神。此外，教师还可以结合所学知识设计难度适宜的探究问题，帮助学生了解所学内容的探究过程，进而深化学生对知识点的理解。

举例来说，在学习“集合与逻辑”一课时，教师可以利用教材中“数学文化”模块的内容教学。首先，教师应向学生介绍德·摩尔根在逻辑学领域发明了一套适合推理的符号，并以代数的方法研究逻辑的演算，并将逻辑学放在了集合的基础上。¬(p∧q)⇔¬p∨¬q、¬(p∨q)⇔¬p∧¬q被称为德·摩尔根定律，在当时的环境中得到了广泛的应用。接着，教师向学生展示集合运算和补集的运算定律：（两集合之交的补等于两集合补集之并）；（两集合之并的补等于两集合补集之交）。利用多媒体将集合运算、补集运算定律及德·摩尔根定律对比展示，并引导学生观察，如果将两组公式中的命题p和q换成集合的A与B，将∨与∧换成集合运算中的⋂和⋃，否定算符¬换成补集的运算，则两组公式是相通的。由此，学生可以认识到，虽然德·摩尔本人并没有提出集合的系统理论，但他对逻辑理论的研究却直接推动了集合的出现，这间接说明了逻辑与集合之间有着深刻的内在联系。除此之外，教师还可以向学生介绍其他有贡献的科学家故事，如康托尔发现了“无穷集”，并主张有理数与自然数一样多，线段上的点和直线上的点一样多，直线上的点和平面上的点一样多，也与空间的点一样多。这一主张为数学发展带来了一场革命，由于他的理论超越了直观，所以受到了很多人的反对，并且还有部分人对他进行了指责，双方争辩长达十年之久。基于此，通过介绍数学家故事、再现发展历程等方式，能够有效地在课堂中渗透数学文化，增加课堂趣味的同时，也能让学生受到文化的熏陶，有助于学生形成良好的学习品质与习惯。

2.在数学应用中渗透数学文化

数学是一门理论与实践相结合的科目，学生在学习中不仅要掌握理论知识，还要学会应用知识来解决问题。但在传统教学过程中，部分教师忽视了数学教学与实际应用之间的关系，导致很多学生认为数学脱离实际，较为枯燥。为了解决这一问题，教师应重视挖掘教材中所涉及的应用因素，以创设情境的形式引导学生对数学思想的掌握，以此来渗透数学文化并培养学生的应用意识。

举例来说，在学习“抽样”一课后，为了锻炼学生运用知识解决问题的能力，教师可以教材中的“数学文化”模块为背景创设情境，并提出问题引导学生思考。首先，课堂中先展示教材中“《文学摘要》的破产”相关内容，并提出问题：历届美国总统选举中，《文学摘要》都做了正确的预测，具有一定的威信力，但在1936年美国总统选举中，《文学摘要》的预测却出现了错误，想要了解它预测失败的原因，应该先了解什么呢？学生结合所学知识提出应检查抽样调查方案，教师在指导学生阅读教材的基础上，为其提供其他素材，让学生自行展开分析。学生通过了解后得知，《文学摘要》当时是将问卷分发给了1000万的选民，而选民的确定并不是随机的，而是在电话簿、俱乐部会员名单中产生。教师鼓励学生以小组为单位，根据搜集到的资料进行分析，小组成员讨论后认为，《文学摘要》的调查结果不具备参考性，根据当时的大环境，安装电话的应是少数富裕的家庭，能成为俱乐部会员的更不会是穷人，因此《文学摘要》的调查方案漏掉了基层民众或是经济基础较差的穷人，导致抽样方案缺乏公平性。由此，学生可以认识到抽样方案的设计应当公平地对待每个样本群体，这样才能避免样本出现偏差。其次，教师设计实践活动：以小组为单位，对本年级同学每天完成作业的时间进行一次抽样调查，规定样本量n=100，设计一个合理的调查方案和一份调查问卷，并具体实施一次抽样调查工作。这样，教师不仅在课堂教学中渗透了数学文化，还通过设计实践活动锻炼了学生的应用意识。

3.通过感受数学美渗透数学文化

著名数学家华罗庚认为，数学本身是千姿百态、引人入胜的，认为数学枯燥乏味的人，是因为没有体会出数学的内在美。新课标中也倡导教师在教学中应体现出数学的美学价值，由此可见，数学美也是数学文化中的重要组成部分，体现在文字、图像等多个方面。教师可以借助数学美来渗透数学文化，这不仅能够激发学生的数学兴趣，还能提高其发明创造能力，使学生的审美能力和学习效果大大提升。

举例来说，在学习“函数的奇偶性”一课时，教师应结合多媒体向学生展示函数中的对称美，让学生在掌握数学知识的基础上，对数学文化有一定的认识。如教师应鼓励学生认真观察图1内容，并思考它们有什么共同点。

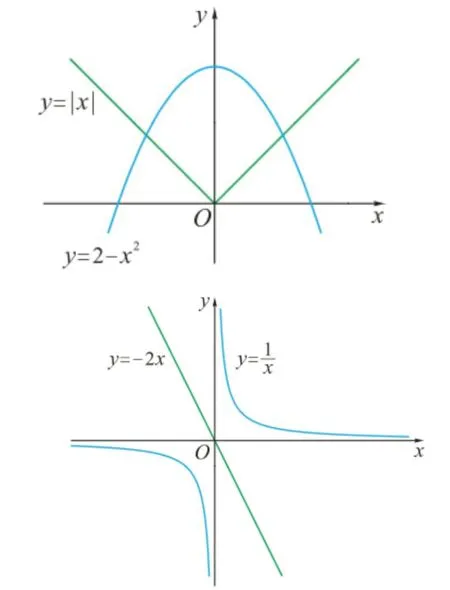
图1

学生在观察后发现左侧两个图像是以y轴为对称轴的对称图形，右侧图像则是以原点为中心的中心对称图形。借助图片不仅可以充分调动学生的积极性，引导学生发现图像关于y轴或原点对称，还可以引导学生总结奇偶函数的特点，深入体会到数学的美。之后，为了强化学生对奇偶函数定义的掌握和运用，教师应设计习题：请利用定义来判断下列函数的奇偶性f(x)=x3+2x。学生在利用定义解题时，需要先画出函数图像，求出定义域，看其是否关于原点对称，之后，再计算f(-x)=f(x)的关系，如果f(-x)=f(x)，则为f(x)偶函数；如果f(-x)=-f(x)，则f(x)为奇函数。由此，学生会在解决问题的过程中，对奇偶函数定义有更深入的了解。如此，教师在教学中凸显了数学的对称美，合理地渗透了数学文化，还引导学生自行发现了图像的对称性质，有效提高了课堂教学效率。

（二）凸显人文，提高学生数学修养

高中数学教学阶段，教师可以明显地感觉到班级学生数学学习呈两极化趋势，部分学生认为数学是抽象的，是枯燥乏味的，想要学习好数学，就要在课堂中认真听讲，课后还要对定理、公式“死记硬背”。另一部分学生则认为数学是有趣的，利用所学知识解决问题，很有成就感。这种现象导致了学生的数学水平差距拉大，不利于学生全面发展。针对这一情况，教师在教学中要重视体现数学的人文性，将数学知识所蕴含的文化背景展示在学生眼前，让其认识到数学与生活之间的密切联系，从而促进学生数学修养和能力的提升。

举例来说，在学习“三角函数模型的简单应用”一课时，为了让学生认识到数学与生活之间的联系，教师在课堂初始可以设计这样的导入方案：首先，用多媒体展示视频，同时用语言引导学生思考：同学们看过海宁潮吗？今天带领大家去看一看天下奇观——海宁潮。学生观看视频后，教师引导学生思考：潮起潮落中也蕴含着数学知识，大家能结合已掌握的知识说一说你发现的数学知识吗？学生根据教师的提问，思考后回答：涨潮和退潮之间蕴含着三角函数知识。教师要给予学生一定的鼓励，并展示多媒体视频，让学生观察“物理中单摆对平衡位置的位移与时间的关系”“交流电中的电流与时间的关系”“声音的传播”等现象，引导其归纳总结这些现象中也包含三角函数知识。这样通过视频，教师能够让学生在熟悉的情境中进入课题，激发学生对数学学习的热情和兴趣，让学生认识到生活离不开数学，体会到学习数学的重要性。同时，学生还能对三角函数的文化特性有更深刻的认识，有利于激发学生的探究动力，使高中课堂教学氛围变得活跃起来，为后续教学奠定良好的基础。教师还可以展示三角函数图像并提出问题，以图像为切入点，带领学生探究三角函数模型的解析式，让学生在明确学习任务和目标的基础上，有目的地参与到教学活动中。在教师的指导下，学生可以从图像中获取信息，并强化对函数概念的理解和掌握，注意自变量的变化范围，初步掌握三角函数模型的应用。

（三）开展活动，合理融入数学文化

在数学课堂中设计形式多样、内容丰富的活动，不仅能够有效吸引学生的注意力，还有助于数学文化的渗透。在实际教学中，教师要结合学生的身心发展特点和教学目标，设计数学游戏、实践探究、智力竞赛等活动，并创设生动、有趣的情境吸引学生的注意力，使学生主动参与其中。这样不仅可以为数学文化的渗透提供渠道，还能够拓展学生的知识面。

举例来说，在学习“函数”一课时，为了强化学生对数学概念的理解和掌握，教师可以设计探究活动。首先，教师应利用多媒体展示PPT动画，并简要概述函数的发展史，通过教师的讲解学生可以认识到，从17世纪伽利略提出“几何观念下的函数”，到18世纪欧拉在代数观点的基础上赋予函数新的思想，再到19世纪傅里叶发现对应关系下的函数，人们并没有结束对函数概念的探索，而是在不断地努力和研究。教师提出问题：同学们，在初中数学学习中，也曾接触过数函数的概念，请大家回忆一下。随机选择学生说出答案，并在学生回答的基础上进行总结。由此，学生可以将新旧知识进行有效衔接。其次，教师要求学生自行阅读教材，并提出问题：阅读教材中的例1、2，并思考:（1）函数变量的取值范围？（2）变量t的变化范围？（3）在取值范围中，任取一个t值，是否有唯一、确定的变量值与之相对应？鼓励学生分组交流、讨论，并回答上述问题，在学生大胆表达自己的想法和观点后，由教师加以补充和完善，最后与学生一起尝试总结函数概念。这样，教师以数学文化为暗线，以数学应用为明线，结合教材中的例题，引导学生自行探究和分析，从而明确了函数变量的关系，进而强化了学生对函数概念的理解，使教学效率得到提升。

三、结语

总的来说，数学的发展形成了丰富的文化内涵，它不是空泛的理论，而是集多个要素、集理论与实践为一体的学科。当下高中数学课堂中渗透数学文化已经成为教育界普遍认同的理念，在实际教学中，教师应发挥自己的专业素养，将数学文化合理地渗透到真实的教育环境中，并重视反馈，不断优化教学设计，真正落实“知行合一”。