基于Marchenko理论的成像域与数据域层间多次波消除方法对比

张乐乐， 邵婕， 郑忆康， 王一博， Evert Slob

1 中国地质大学地球物理与空间信息学院， 地球内部多尺度成像湖北省重点实验室， 武汉 430074 2 中国科学院地质与地球物理研究所， 北京 100029 3 Delft University of Technology, 2628 CN Delft, The Netherlands

0 引言

传统的偏移成像技术通过对野外观测数据进行处理来获得地下的结构信息，指导油气资源的勘探开发. 然而，传统的偏移成像理论基于“一次反射”的假设. 该假设使得传统的偏移成像技术可以准确的处理观测数据中的一次反射波(一次波)，而多次反射波(多次波)则会在偏移成像结果中产生假象，不利于油气资源的勘探开发. 为了解决偏移成像结果中多次波假象的问题，很多专家学者提出了各种解决方法，主要分为多次波消除和应用两个方向.

自由表面多次波由于具有较强的振幅，通常会在偏移成像结果中产生较强的假象.SRME(Surface-Related Multiple Elimination)(Verschuur et al., 1992)和EPSI(Estimation of Primaries by Sparse Inversion)(van Groenestijn and Verschuur, 2009)作为两种消除自由表面多次波的方法，已经在工业界得到了广泛的应用. 其中，SRME不需要任何速度信息，可以成功预测所有阶数的自由表面多次波. 但是，SRME预测的自由表面多次波相位准确但振幅不准确，需要借助匹配相减算法来消除观测数据中的自由表面多次波. EPSI则基于反演理论来提取观测数据中的一次波，该方法避免了SRME技术的多次波预测和匹配相减，从而避免了匹配相减对一次波的损害. 以上两种方法在野外观测数据中均得到了成功的应用. 自由表面多次波成像也成为了近年来的研究热点(Brown and Guitton, 2005; Whitmore et al., 2010; Verschuur and Berkhout, 2011; Wang et al., 2014, 2017; Lu et al., 2015). 在使用相同的观测数据偏移成像时，自由表面多次波可以提供地下更广的覆盖范围，同时在偏移结果中也会产生假象. 相比于自由表面多次波，层间多次波产生机制更复杂，更难被消除. Araújo等(1994)基于逆散射级数的第三项推导出了逆散射级数法来消除观测数据中的层间多次波(Weglein et al., 1997; Ten Kroode, 2002; Löer et al., 2016). 该方法不需要任何速度信息，可以一次性预测所有阶数的层间多次波. 但是，由于预测的层间多次波振幅不准确，需要借助匹配相减来消除观测数据中的层间多次波. Berkhout(2014)提出了全波场偏移理论，该方法可以利用层间多次波成像并已经在野外观测数据中进行了成功的应用(Davydenko and Verschuur, 2018).

近年来，Marchenko成像技术(Slob et al., 2014; Wapenaar et al., 2014)得到了国际勘探地球物理学界的广泛关注. 该技术可以理解为一种基于Marchenko理论的成像域层间多次波消除方法. 相比于传统成像技术，该方法在相同输入数据的条件下，可以获得地下结构不含多次波假象的像. 基于聚焦点投影到观测系统面后的Marchenko方程组(van der Neut and Wapenaar, 2016)，Zhang和Staring(2018)提出了MME(Marchenko Multiple Elimination). 该技术是一种完全数据驱动的多次波消除方法，不需要任何速度信息，可以准确预测所有层间多次波的振幅和相位信息，从而可以外科手术式的消除观测数据中的层间多次波，避免了匹配相减对相关一次波的损害. 同时，基于修正的Marchenko方程组，Zhang等(2019)提出了T-MME(Transmission compensated Marchenko Multiple Elimination).该方法不仅可以在数据域外科手术式的消除层间多次波，还可以补偿一次波中的透射损失. Zhang和Slob(2019)将以上两种方法进一步推广来处理自由表面多次波和鬼波，使得MME和T-MME方法可以将鬼波、自由表面以及层间多次波一步消除. 合成数据和野外观测数据测试证明了以上两种方法的有效性(Zhang and Slob, 2020a). 相关技术已经在工业界得到了成功的应用.

本文对基于Marchenko理论的成像域和数据域层间多次波消除技术进行了对比分析，给出了两种方法详细的理论及数值模型试算结果，并对两种方法的优缺点进行了讨论.

1 基于Marchenko理论的成像域层间多次波消除技术

我们将基于Wapenaar等(2014)对Marchenko成像理论进行详细的回顾并进行二维合成数据测试. 在本小节及后续的数据域层间多次波消除技术推导过程中，我们假设观测数据子波宽度无限小. 假设介质不存在自由反射界面，基于褶积和互相关类型的互易定理推导得到的单边格林函数表示定理可以表示为(Wapenaar et al., 2014)

(1)

(2)

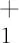
(4)

=δ(x″0-x0)δ(t),

(5)

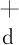
图1 聚焦函数和格林函数示意图(这里用源点和检波点互易定理来表示格林函数)

(6)

(7)

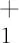
(8)

(9)

(10)

这里，R(x′i,xi,t)为震源和检波点均位于界面∂Di上时界面∂Di以下介质的反射响应，该响应可以通过MDD(Multi-Dimensional Deconvolution)从公式(10)求取.R(x′i,xi,t)中零时刻零偏移距的值R(xi,xi,t=0)即为聚焦点xi的反射系数，也可以称之为点xi的像.通过计算目标区域所有成像点的反射系数，即可获得该区域的成像结果.这里，基于Marchenko理论的成像域层间多次波消除技术只利用一次波进行成像，成功的在成像域消除了多次波对成像结果的影响.

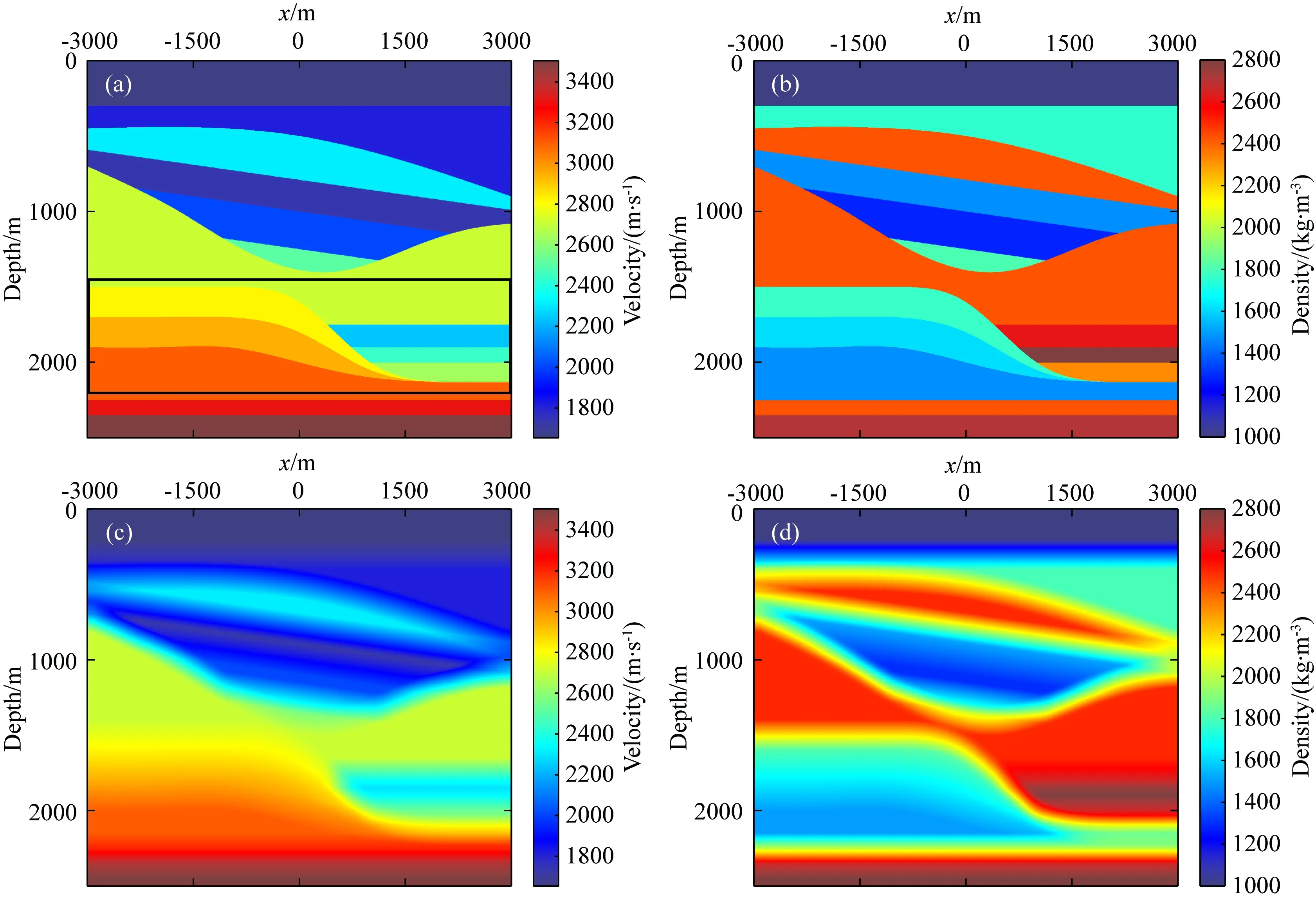
图2 速度与密度模型以及平滑速度与密度模型

图3 模拟的波场记录

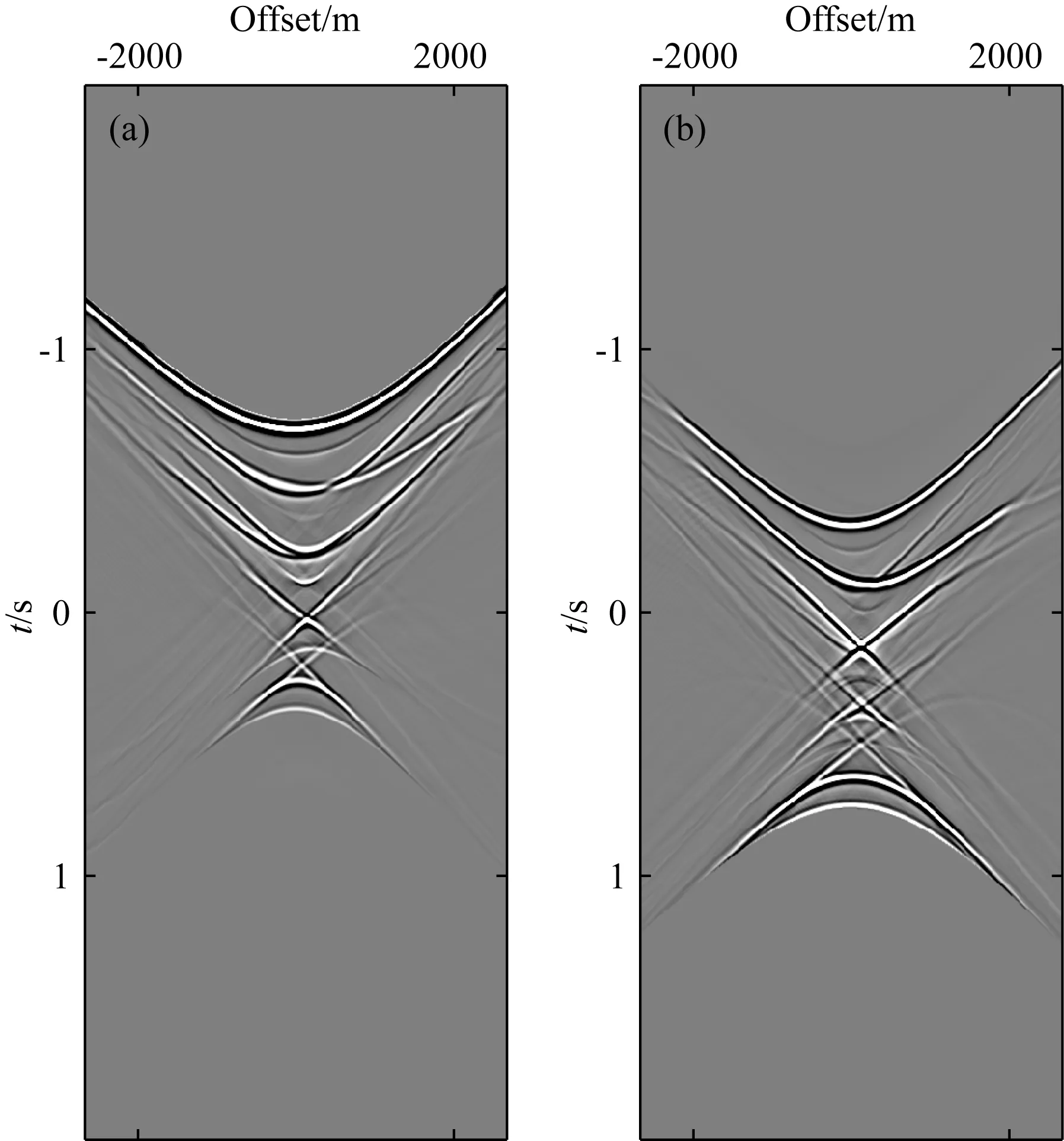
图4 经过20次迭代求得的上下行聚焦函数

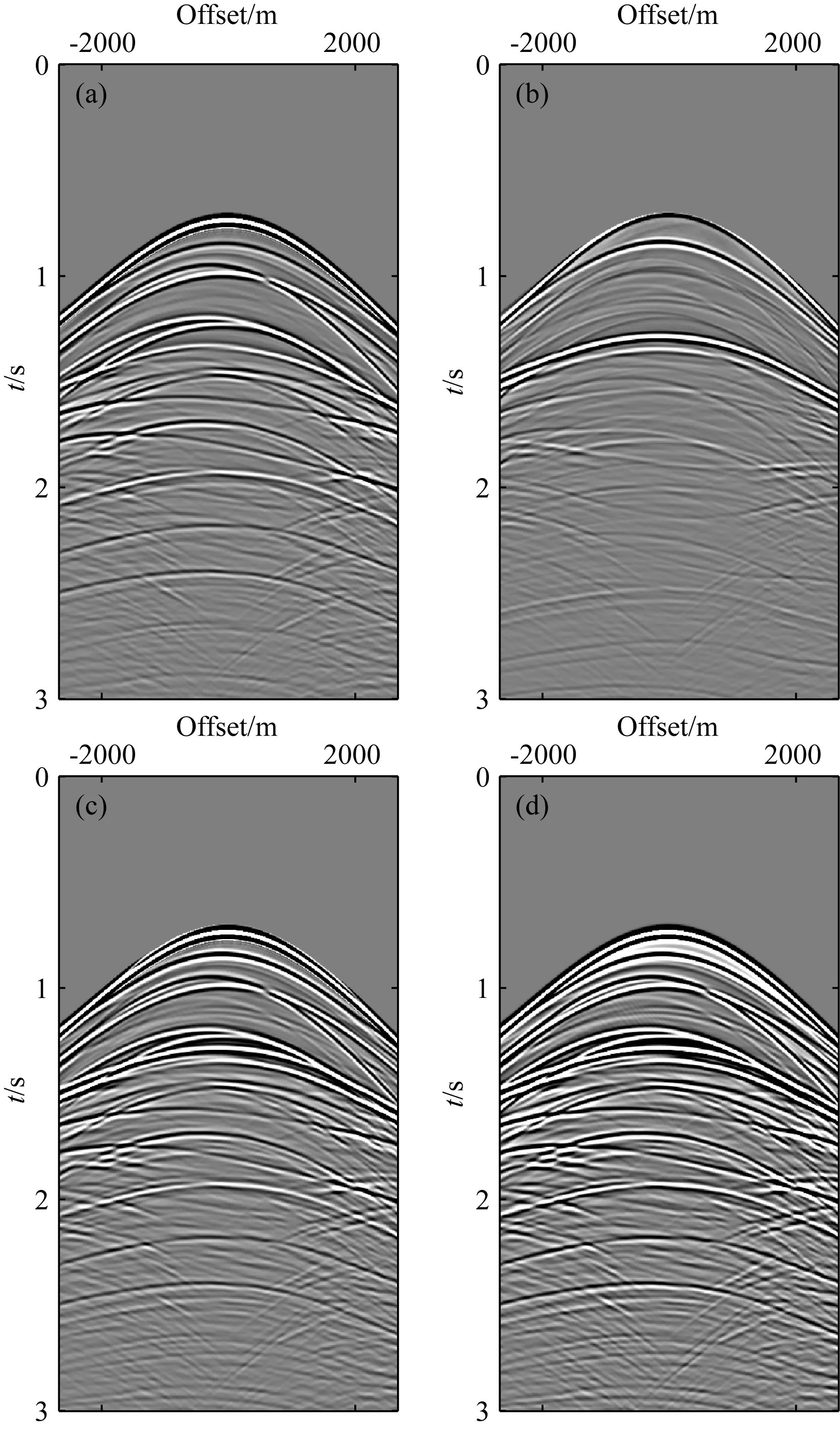
图5 求得的格林函数

图6 零偏移距道波形对比.红色虚线表示图5c中的零偏移距道，蓝色实线表示图5d中的零偏移距道.两道的振幅均做了归一化.

图7 偏移/成像结果对比

2 基于Marchenko理论的数据域层间多次波消除技术

(11)

(12)

其中：

(13)

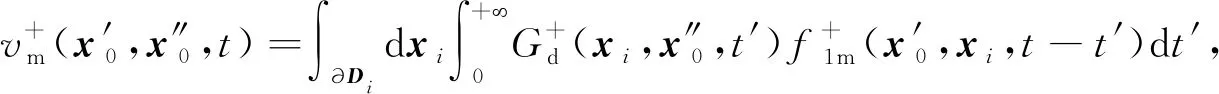
(14)

(15)

(16)

(17)

为了方便后续推导，我们将公式(16)和(17)改写为如下形式：

(18)

(19)

(20)

公式(20)按Neumann级数展开可得：

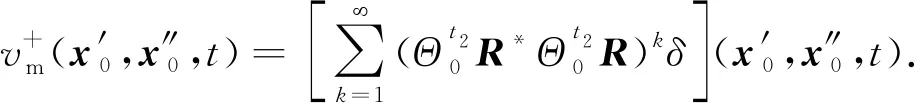
将公式(21)代回公式(11)可得：

(22)

图8 上下行聚焦函数与做多维褶积之后得到的v±和上下行格林函数与做多维褶积之后得到的U±示意图

Rt(x″0,x′0,t=t2)=R(x″0,x′0,t2)

(23)

这里，Rt是提取的一次波.当t2依次取观测数据中每一个时刻时，Rt则成功提取了地下各反射界面的一次反射波.公式(23)所示方法消除层间多次波的过程中，不需要任何速度信息.

我们继续采用图2所示的二维模型来详细说明MME理论的处理流程及其有效性.利用Thorbecke等(2021)所发表的开源代码对数据域层间多次波消除技术进行测试.图9a是震源位于(0 m, 0 m)的模拟波场.我们以模拟波场作为公式(23)的输入进行多次波消除.其中，R和R*取模拟的所有炮集，R取震源位于(0 m, 0 m)的炮集.迭代次数k=10,15,20所对应的Rt如图9b,9c和9d所示.对比图9a与9d，R中所有的层间多次波均被成功消除，Rt只包含地下各界面的一次反射波.我们从图9a和图9d各提取零偏移距道做波形对比.如图10所示，MME技术在成功消除多次波的同时完整的保留了一次波的信息.图11a给出了模拟波场的目标成像区域逆时偏移结果，其中包含层间多次波的假象.图11b给出了Rt(k=20)目标成像区域逆时偏移结果，该结果准确的给出了图2a所示目标成像区域的结构信息，不包含多次波假象.

图9 模拟波场和k=10,15,20所对应的消除多次波后的波场

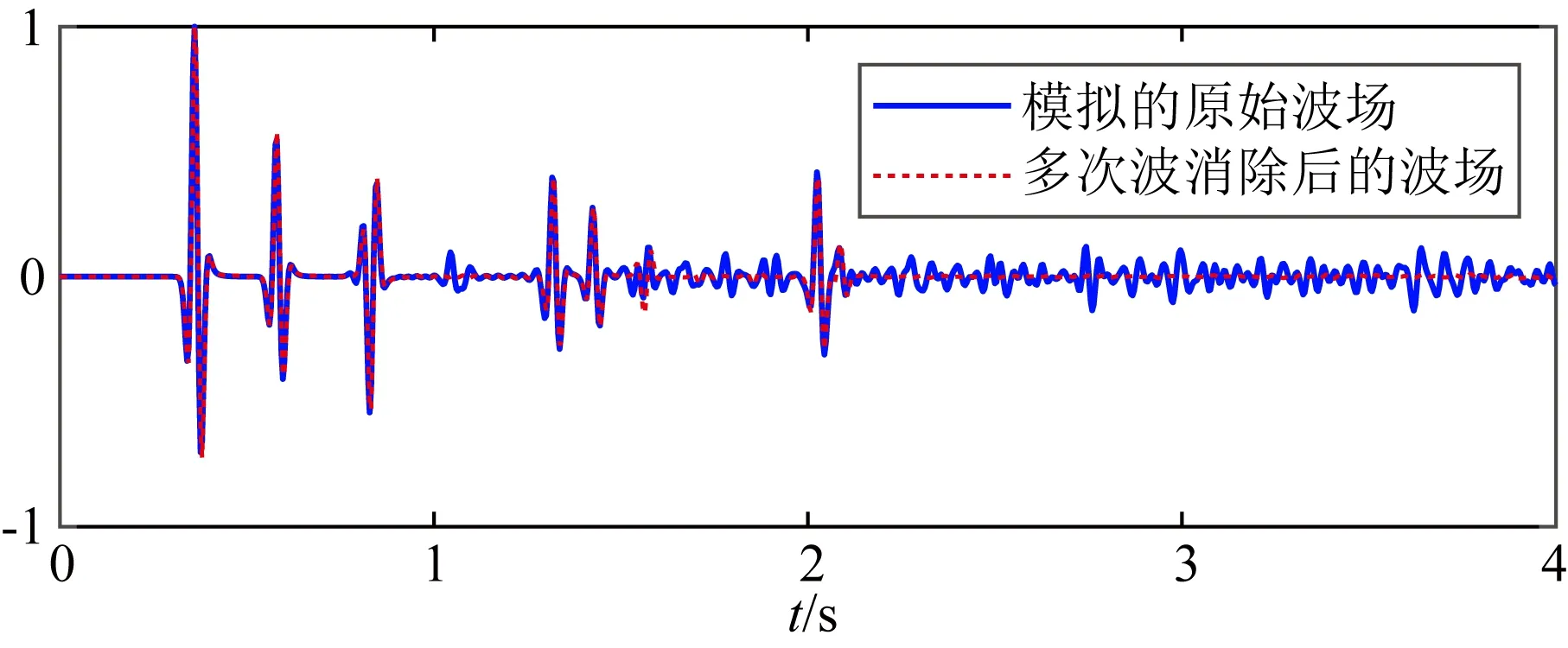
图10 零偏移距道波形对比.蓝色实线表示图9a中的零偏移距道，红色虚线表示图9d中的零偏移距道.两道的振幅均做了归一化

图11 逆时偏移结果对比

3 讨论

基于Marchenko理论的成像域层间多次波消除技术以预处理之后的观测数据作为输入，可以在成像域成功消除层间多次波，对地下结构进行准确的成像.如图7b所示，成像结果给出了图2a所示模型中成像区域不含多次波假象的像.MME作为数据域层间多次波消除方法，不需要任何速度信息和匹配相减，可以将预处理之后的观测数据中所有阶数的层间多次波成功消除(如图9d所示).基于消除多次波之后的数据，后续的速度建模、AVO/AVA分析以及偏移成像均可以得到更精确的结果.因此，尽管基于Marchenko理论的成像域和数据域层间多次波消除技术均可以成功消除层间多次波，但在勘探地球物理领域，数据域层间多次波消除技术具有更广阔的应用前景.

成像域和数据域层间多次波消除技术都是基于褶积和互相关类型的互易定理推导而来的，只适用于非衰减介质.在强衰减介质中，两种方法可以部分的消除多次波.此外，震源子波反褶积的质量也会影响两种方法的表现，主要原因在于不准确的震源子波反褶积会导致观测数据振幅误差，从而使得成像域层间多次波消除技术获得的成像结果中出现多次波假象的残余，数据域层间多次波消除方法获得的结果中多次波不能被完全消除.还有，两种多次波消除方法均要求观测数据空间采样密度较高.因而，海上数据近道缺失的情况也会限制两种方法的表现.在野外观测数据的处理过程中，当使用条件满足的情况下，两种方法均可以获得相比于常规理论更好的结果(Jia et al., 2018; Zhang and Slob, 2020a).

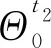
4 结论

基于Marchenko理论的成像域和数据域层间多次波消除技术是勘探地球物理领域前沿的多次波消除技术.成像域层间多次波消除技术可以在成像域消除多次波，准确的对地下地质结构成像.MME作为一种完全数据驱动的方法，不需要任何速度信息和匹配相减，可以在数据域成功消除观测数据中所有阶数的层间多次波.本文对两种方法相关的理论做了回顾和总结，采用二维模型对两种方法的处理流程和有效性进行了详细的对比和说明，并就两种方法的优缺点进行了讨论.

致谢感谢荷兰代尔夫特理工大学Delphi研究组的赞助商对本研究的支持.