Dijkstra算法在BIM审查中的应用
文|北京构力科技有限公司 魏重洁 王委 王嘉 何启明;中交天津港湾工程研究院有限公司 宋博文
0 引言
BIM 技术对于促进建筑全生命周期的信息化具有重要的意义,目前在实际项目中的应用颇为广泛。随着BIM 技术的普及,BIM 信息化数据审查的意义也逐渐凸显[1-2]。传统的二维施工图审查并没有真正的实现智能化审查,需要审查工作人员对提交的二维图纸进行全专业的审查工作,将存在以下问题:问题(1):在审图过程中,由于审图人员对规范的理解、专业水平、经验以及审查尺度等不一致,这会造成审查结果的不一致。问题(2):由于审查工作涉及的专业众多,需要审查的规范众多。随着各个专业的飞速发展,各个专业所涉及审查规范的版本也在不停的更新之中,审查工作量大。在审图工作进行时,存在挑选重要审查部位进行针对性审查。由此,造成了审查工作的不全面,规范条文漏审的情况。问题(3):政府管控难。主管部门无法及时获取施工图审查过程中各环节存在的问题,对施工图设计、审查质量的真实情况难以准确掌握,监管的有效性和时效性均不能得到保证。针对以上问题,2017年湖南省以工程建设项目三维数字报建为切入点开启基于BIM 模型的施工图数字化审查。2019年,指导各地开展城市信息模型(CIM)基础平台建设,推进智慧城市建设,北京、雄安、广州、南京、广州、厦门、雄安等多个城市被住房和城乡建设部列为城市信息化建设和建筑信息模型审查的试点城市[3-6]。
随着建筑信息化审查工作的开展,具体条文内容的审查以及建筑信息化数据的处理方法也成为数值化审查工作中的重点工作。特别是对应建筑消防的数字审查工作,如建筑消防审查参考的一个主要规范《建筑设计防火规范》(GB 50016-2014,2018年版)[7]。这本规范中5.5.17 对于疏散路径的审查,需要对审查模型中的疏散路径进行计算后与规范数值进行比对。模型中疏散路径的计算一直都是数值化审查中的难点,针对该问题,本文将Dijkstra 算法应用到BIM 审查的数字计算中,更为准确的求除疏散路径。
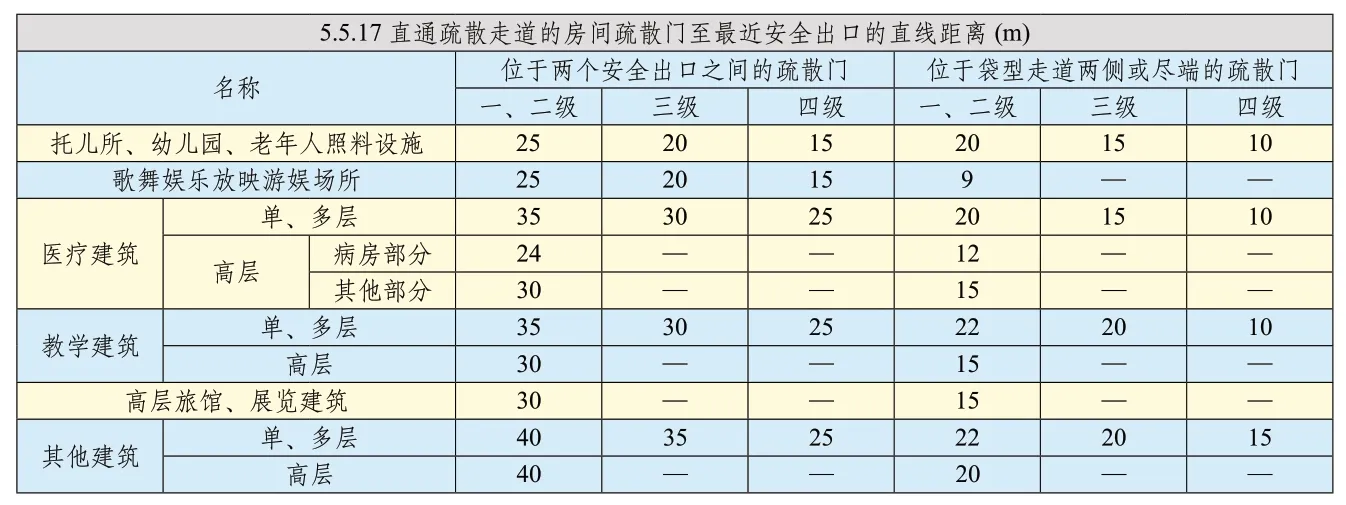
表1 防火规范中疏散距离的规定
1 Dijkstra 算法
Dijkstra 算法处理的是一组结点集合数据中各个节点到其他节点的最短路径。用于解决最短路径问题的算法被称做“最短路径算法”,有时被简称作“路径算法”。最短路径问题是图论研究中的经典算法问题。最常用的路径算法有:Dijkstra 算法、A*算法、SPFA 算法、Bellman-Ford 算法和Floyd-Warshall 算法[8-11]。本文中主要正对Dijkstra 算法在消防审查中疏散路径问题的应用进行描述。
为更好得理解Dijkstra 算法,如图1所示,现有结点集合S=[P1、P2、P3、P4、P5、P6]以及其各节点之间的路径信息,①为结点编号,-3-为路径信息,各个结点之间双向距离相等,再应用Dijkstra 算法对已知结点集合S 求其最短路径。依据图1的路径星系,第一步列出一个二维数据结构,储存结点集合S 中各个结点之间的直接路径数据,形成表2所示的对称的二维矩阵。
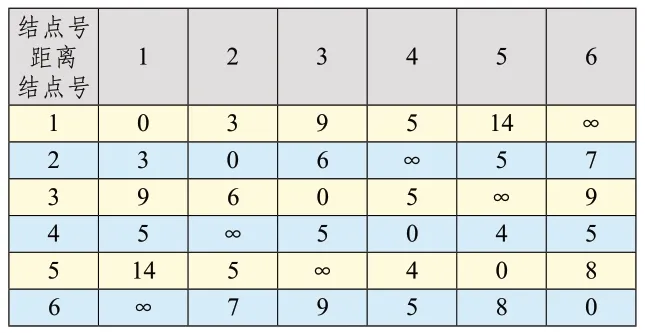
表2 直接路径信息储存表
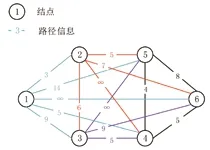
图1 结点集合以及其路径线示意图
第二步以结点1 直接到达各个结点的路径距离为结点1 到各个结点的初始最短路径距离,求到结点1 路径最短的那个结点。根据最初的直接路径信息储存表可以确定,结点1 的路径最短结点为结点2,并可以确定结点1 到结点2 的最短路径为直接到达的路径,即结点2-结点1。计算结点1 通过结点2 到达各个结点的路径,并且将该路径值与结点1 直接到达各个结点的路径距离对比,取两者的最小值,可以得到结点1 各个结点的最短路径距离如表3所示。可以发现结点5、结点6 到结点1 的最短路径得到了刷新。
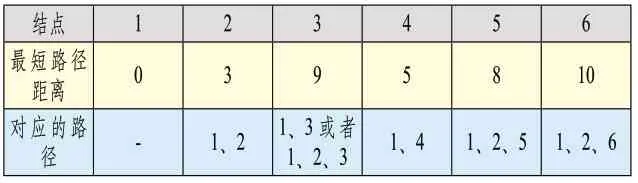
表3 通过结点2 刷新的最短路径
第三步获取通过结点2 刷新的最短路径的最短路径结点(除结点2 外),可以确定此时的最短路径结点为结点4,并且可以确定此时结点4 到结点1 的最短路径为直接到达路径,即结点4-结点1。计算结点1 通过结点4 再到各个结点的路径距离,并与表2中的路径距离对比,取两者的最小值,可以得到结点1 到各个结点的最短路径距离如表4所示。在该步骤比较中,并没有最短路径得到刷新。
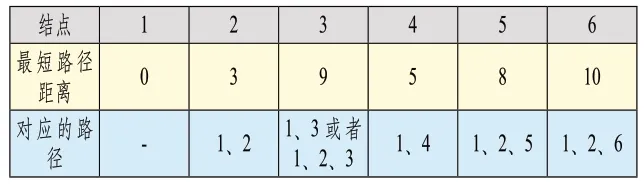
表4 通过结点4 刷新的最短路径
第四步获取通过结点4 刷新的最短路径的最短路径结点(除结点2、结点4 外),可以确定此时的最短路径结点为结点5,并且可以确定此时结点5 到结点1 的最短路径为结点5-结点2-结点1。计算结点1 通过结点5 再到各个结点的路径距离,并与表3中的路径距离对比,取两者的最小值,可以得到结点1 到各个结点的最短路径距离如表5所示。在该步骤比较中,并没有最短路径得到刷新。
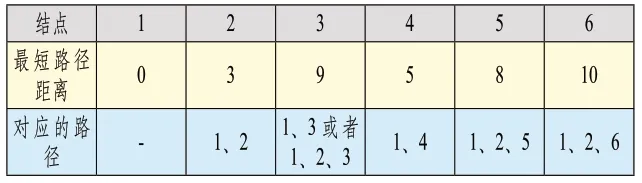
表5 通过结点5 刷新的最短路径
第五步获取通过结点5 刷新的最短路径的最短路径结点(除结点2、结点4、结点5外),可以确定此时的最短路径结点为结点3,并且可以确定此时结点3 到结点1 的最短路径为结点3-结点2-结点1或者结点3-结点1。计算结点1 通过结点3 再到各个结点的路径距离,并与表4中的路径距离对比,取两者的最小值,可以得到结点1 到各个结点的最短路径距离如表6所示。在该步骤比较中,并没有最短路径得到刷新。
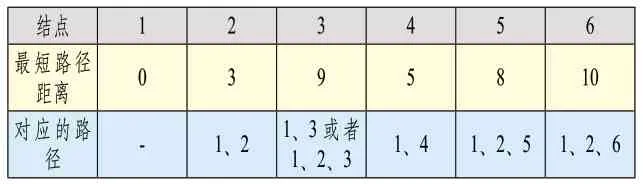
表6 通过结点3 刷新的最短路径
2 Dijkstra 算法的应用
2.1 计算前处理
在进行实际样例模型计算之前,需要对实际样例模型进行简化处理。获取Revit模型的房间内轮廓线以及疏散门、安全出口的位置点。如图2所示,在对求图中各个房间的疏散门到疏散走道的安全出口之间的疏散距离,即疏散门到安全出口的最短路径。在求最短距离问题时,可以将房间内的疏散距离转化为特征点之间最短路径问题。特征点集合由疏散走道的轮廓线端点、疏散门以及安全出口的位置点组成,即S=[P1、P2、P3、P4、P5、P6、P7、P8、P9、P10]。如图2所示,分别计算点集合S中P3、P4、以及P6 到P9 的最短路径。
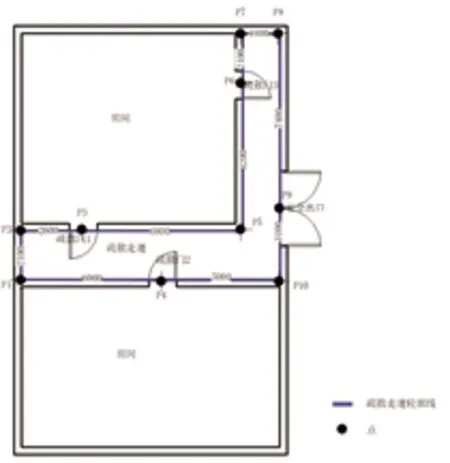
图2 样例模型示意图
如图3所示,在对点集合进行计算时,我们需要根据各个点之间的实际距离确定各个结点之间的路径距离,即取样例模型中各个结点的连线长度。需要注意,在实际问题中,当两点直线连线穿越墙体时,人在疏散时无法按照该直线距离逃生,该疏散路径可直接丢弃,即将两点之间的路径距离直接赋值正无穷大,进行后续计算。
2.2 Dijkstra 计算
在计算如图3所示的样例模型时,先根据Dijkstra 算法,算出所有结点到其他结点的最短路径。
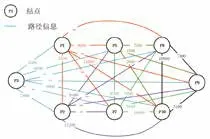
图3 样例模型Dijkstra 算法路径线示意图
第一步:
求出各个结点之间的距离,并存入一个二维数组D[10,10],作为P1 结点到第P10 个结点之间的初始最短距离;
初始化一个一维数组Length,并存入P1 结点到其他结点的距离;
初始化一个一维数组Used,并存入Pi结点是否被遍历,序号为0 即Used[0]=true,其他为false;
初始化一个字典,并存入P1 结点的最短路径所经过的结点序号。
第二步:
初始化一个最小值dMin=double 值的最大值;
初始化一个序号k=0,即P1 结点在S中的序号;
循环所有的结点,找到没有被遍历过的结点中距离P1 最短的结点Pm(dMin=P1至Pm 之间的距离),并将k 刷新为结点Pm的序号m-1,数组Used[k]刷新为true。
循环所有的结点,找到没有被遍历过的结点Pn,如果Length[n-1]大于dMin 加上D[m-1,n-1](即结点P1 到结点Pn 的距离大于结点P1 通过结点Pm 到结点Pn 的距离),则刷新数组Length 的值,Length[n-1]=dMin+D[m-1,n-1],并更新字典中最短路径的结点序号。

表7 疏散门至安全出口的最短路径
第三步:
重复第二步,直至所有点集S 中结点被遍历,以此求得各个结点到其他结点的最短路径。
在求得所有结点到其他结点的最短路径后,分别获取P3 至P9,P4 至P9 以及P6 至P9 的最短路径,如图4所示。
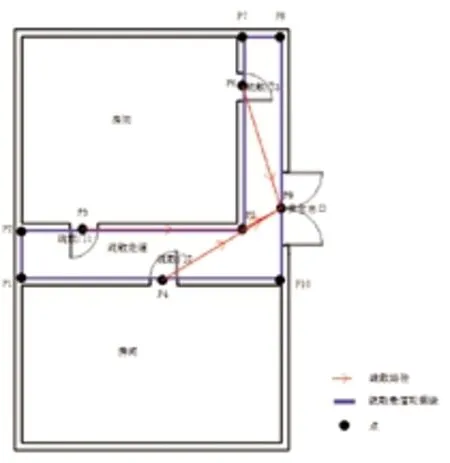
图4 初始疏散路径结果
2.3 结果后处理
通过Dijkstra 算法对样例模型进行计算,我们能够得到疏散门位置点到安全出口位置点的距离。
实际最短疏散距离还需要对比疏散门边到安全出口门边的距离,此时只需要对比各个疏散门位置点与两个门框在疏散路径的最短距离,可确定为最终的疏散路径,如图5所示。
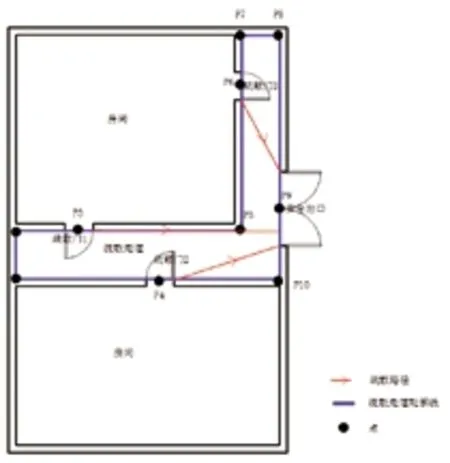
图5 疏散路径结果
2.4 计算结果在审查中的应用
将以上求解的疏散路径结果应用以实际项目的审查之中,如图6所属的项目,疏散门到安全出口的最短路径为33.116m,不满足5.5.17 中疏散门至安全出口的疏散距离应该小于等于15m 的要求。
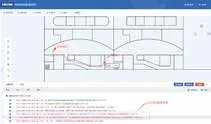
图6 疏散路径算法在审查项目中的应用
3 结论
本研究将Dijkstra 算法应用到BIM 审查的数字计算中,对《建筑设计防火规范》(GB 50016-2014,2018年版)中5.5.17条文中的疏散门到安全出口的疏散路径进行计算。将房间轮廓线的两个端点以及疏散门、安全出口的位置点作为特征点集合,应用Dijkstra 算法对特征点集合进行计算。将得到的初步疏散路径再次经过门宽部分最短路径对比,得到最终的疏散路径。根据计算的最短路径,与规范5.5.17 中的相关规定进行比对,以此审查出不满足规范的距离。

