RVM在煤自燃预测中的应用研究

王 丹

(晋能控股煤业集团 四老沟矿，山西 大同 037000)

矿井采空区遗煤自然发火不但对矿井安全生产有严重的威胁，而且可能会引发采空区瓦斯爆炸，严重威胁井下作业人员的生命安全[1-2]。有效地预防采空区遗煤自然发火是确保矿井安全生产的重要之举，而准确预测采空区遗煤的自然发火是降低煤自燃对安全生产威胁的关键。在煤自然发火时，采空区遗煤自然发火标志性气体的浓度因煤发生不同氧化程度而改变，所以利用检测检验技术研究自燃阶段各标志性气体浓度的变化对煤自燃温度进行预测分析，实现准确预测煤自然发火程度的目标[3-5]。为此，科研工作者开展了大量的试验研究，利用不同机器学习算法研究分析煤自然发火标志性气体浓度与煤自燃温度之间的变化规律。

PAN Ke等[6]借助RBF神经网络学习方法对自然发火标志性气体浓度与煤自燃温度二者的关系进行研究；邓军等[7]针对目前预测采空区遗煤自然发火标志性气体种类多，且各气体之间关系复杂，存在非线性关系，通过对支持向量机(SVM)进行改进，并与主成分分析理论(PCA)相结合，构建预测采空区遗煤自然发火程度模型，开始预测煤自燃温度，试验结果证明：通过PCA降维改造后的SVM预测精确度明显提高。

RBF神经网络方法在预测煤自燃过程中很容易进入局部最优，形成复杂的网络结构；SVM核函数因受限于Mercer条件，在选择参数方面非常敏感[8]，因此常规的机器学习算法预测煤自燃温度过程中会产生较大误差。

综上所述，本次研究将根据极大似然估计、贝叶斯等，引进相关向量机[9-10](RVM)预测模型对煤自燃程度进行分析，结合标志性气体浓度预测煤自然发火温度。

1 相关向量机RVM回归

RVM回归指利用超参数引入，同时将权值向量假设为零，达到高斯先验分布，实现模型的稀疏特点[11-12]，通过最大边缘似然方法来估计超参数[13]。输入模型具体见式(1)。

(1)

式中：xi为训练集第i组的输入向量；S为训练集样本的数量；RD为D维的实数域。

t定义为由训练样本输出值ti结合而成的目标向量t=[t1,t2,…,ti,…,ts]T，其中ti表示训练样本第i个输出值，i=1,2,…,S。

输入与输出相关向量机(RVM)回归关系见式(2)、(3)：

ti=y(w,xi)+εi

(2)

(3)

式中：w为由S+1维权值wj结合而成的向量，其中j=0,1,…,S，则w=[w0,w1,…,wi,…,ws]T；

εi为第i个噪声误差，εi：N(0,δ2)，N(·)表示高斯分布，δ2表示噪声方差；

y(w,xi)为通过权值计算得到的输出值；

x为通过xi结合而成的矩阵，x=[x1,x2,…,xi,…,xs]T；

k(x,xi)表示由核函数k(xn,xi)结合而成的核向量，k(x,xi)=k(x1,xi)，k(x2,xi)，…，k(xi,xi)，…,k(xS,xi)，n=1,2,…,S。

在训练样本输出值ti各自独立的条件下，训练样本通过极大似然函数表示，具体见式(4)：

(4)

式中：φ为由核函数k(xn,xi)结合而成的核矩阵，φ=[φ(x1),φ(x2),…,φ(xn),…,φ(xs)]T,φ(xn)=[1,k(xn,x1),k(xn,x2),…,k(xn,xi),…,k(xn,xS)]。

假如直接通过最大似然方法求解向量w与高斯噪声方差δ2，那么可能发生“过拟合”问题，将w赋予为零均值、超参数为α先验分布，具体见式(5)：

(5)

式中：α为S+1维超参数向量，α=[α0,α1…,αj,…,αs]T。

根据马尔科夫性质[14]得到，x*(测试输入矩阵)相对应的y*(预测值)概率表达式，具体见式(6)：

(6)

式中：P(w,α,δ2|t)=P(w|t,α,δ2)P(α,δ2|t)。

因P(α,δ2|t)∝P(t|α,δ2)P(α)P(δ2)，“∝”为成比例关系，那么目标向量t的条件分布，具体见式(7)：

(7)

式中：Ω为目标向量t条件分布协方差，Ω=δ2I+φA-1φT，其中对角阵A=diag(α0,α1,…,αj,…,αS)，I为单位阵。

P(y*|t)的等价形式可用式(8)表示：

(8)

y*=μTφ(x*)

(9)

(10)

式中：μ为w后验分布均值，μ=δ-2QφTt；(x*)为由测试样本结合而成核矩阵；Q为w后验分布协方差Q=(δ-2φTφ+A)-1。

2 RVM预测煤自燃方法

图1为采用RVM预测煤自燃的流程，大致可分为6步。

图1 RVM预测煤自燃流程图

1) 井下取一部分气体，测定气体浓度和煤自燃时的温度。构建训练集(x,t)以及测试集(x*,y*)，x表示训练集的输入矩阵、x*表示测试集的输入矩阵；将数据集合元素属性输入，具体输入数据为C(O2)、C(N2)、C(CO)、C(CO2)、C(CH4)、O(CO/CO2)及Vmax，C(·)表示采集气体的浓度，O(a/b)表示2种气体a、b的浓度比值，Vmax表示预测煤自燃期间的温度，主要由两部分组成：测试集的预测温度y*和训练集的测量温度t。

2) 建立xi(训练集输入向量)的高斯核函数，具体见式(11)：

(11)

式中：xn为训练集中第n组的输入向量；xi为训练集中第i组输入向量；λ表示高斯核函数的宽度。

建立高斯核函数主要是为实现训练集的输入矩阵x从低维空间向高维空间映射，达到更好的训练效果[15-16]。

3) 对超参数α与噪声方差δ2进行初始化，之后开始迭代计算，具体见式(12)、(13)。

(12)

(13)

4) 迭代完成条件达到之后，一部分αj开始接近无穷大，相对应的wi等于0；剩下的αj则开始接近有限值，相对应的xj定义为相关向量；训练结束之后，即可获得w和δ2的最佳值。

(14)

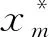
φ*=[φ*(x1),φ*(x2),…,φ*(xn),…,φ*(xs)]T

(15)

(16)

6) 通过训练集获得w和δ2的最优RVM模型，在模型中代入测试集和测试核矩阵，最终计算获得煤自燃期间的预测温度值y*及预测方差δ*2。

3 现场试验

3.1 获取数据

利用煤自燃模拟试验装置检验RVM在煤自燃预测过程中的准确性，试验地点选在晋能控股集团四老沟煤矿，因该矿使用放顶煤开采，采空区遗煤较多，存在遗煤自然发火的危险。为防止采空区遗煤自然发火，设计一种相似于四老沟煤矿井下遗煤供氧与蓄热环境的装置，验证煤自然发火阶段各指标气体浓度与温度的变化规律。

通过设计的煤自燃试验装置——XK型煤自燃试验装置开展试验。此装置主要包括4个部分：气路、炉体、检测和控制，具体如图2所示。炉体形状为圆桶型，内径为0.12 m，装煤最大高度达到0.15 m，最大装煤量为1.5 kg；通过在炉体周围设置保温层以及控温水层来确保炉内煤样拥有稳定的蓄热条件，进气预热紫铜管与电热管子安设在水层内，取气管安设在炉中心轴处。在炉体上下安装气流缓冲层，保证气流能够均匀穿过煤体，通过控温水层加热的空气，其温度能达到煤自燃时温度，可营造一个模拟煤自燃时的环境，之后由炉体底部进入炉内。同时在炉内不同位置安设气体采样点和测温探头。借助SP3430型号的气相色谱仪采集和分析气体，此色谱仪包括3部分：自动取样机、双柱箱、色谱数据处理工作站，具体如图3所示。

图2 试验装置

图3 气相色谱仪装置

借助SP3430型气相色谱仪分析四老沟煤矿的煤自燃特征气体的成分和浓度，结果见表1，挑选30组数据作为训练集，余下的8组数据为测试集。

表1 四老沟煤矿的煤自燃样本数据

3.2 构建模型

构建3种煤自燃预测模型：RBF神经网络、SVM和RVM，3种模型参数设置见表2。

表2 模型参数设置

RVM模型预测煤自燃的实施流程：

1) 对超参数向量α及方差δ2进行初始化处理，同时对最大迭代次数进行设置。

2) 对最大值α进行设置，在RVM迭代阶段，若α大于此最大值时，就判断其接近无穷大，与其相对应的w则为零，那么不再更新该部分值；对方差阈值进行设置，如果其方差的相对误差比阈值小时，就判断完成训练要求，循环结束，退出即可。

3) 通过迭代323次之后，此次试验训练数据基本满足精度要求，其中存在16个αj接近有限值，与其对应的wj不为零，获得RVM模型的最优参数。

4) 利用已训练的模型计算测试样本数据，对工作面采空区煤自燃过程的温度进行预测，同时将其和测量值进行比较分析。

3.3 结果分析

图4为3种方法的预测温度值与测试集真实温度值的对比情况。采用RVM方法预测煤自燃的结果围绕实际值上下浮动，预测精度整体相对较高；采用SVM方法预测煤自燃的精度比RVM方法差一点；采用RBF方法预测煤自燃的结果与真实值相差较大，所预测精度较低，未达到预期效果。

图4 预测结果

图5为3种预测方法的相对误差，其预测相对误差均小于20%，其中RVM预测煤自燃方法的所有样本的相对误差都在10%以下，且体现为集中分布及误差值较小，SVM、RBF预测煤自燃的方法分别存在2个样本的相对误差超过10%.

表3为3种预测方法的平均相对误差。这3种预测方法中，SVM和RBF预测煤自燃的方法所得到的训练误差值相对较低，而得到的测试误差值较高，证明此两种方法具有明显的“过拟合”现象，泛化能力较低；RVM预测煤自燃的方法所得到的测试误差值和训练误差值二者差值较小，具有最大的预测精度。所以RVM预测煤自燃的效果比传统方法(RBF和SVM预测煤自燃方法)要好很多。

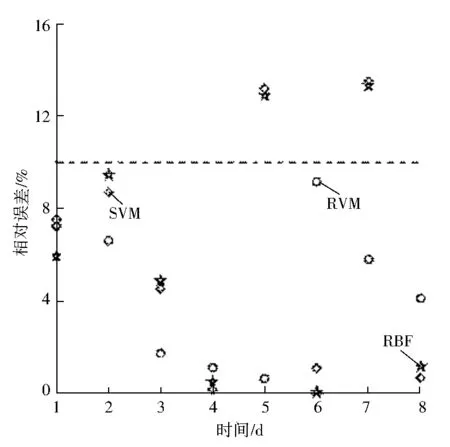
图5 预测相对误差

表3 平均相对误差

4 结 语

以四老沟煤矿煤样为研究对象，模拟煤自燃规律，对自燃阶段所产生的特征气体及浓度、自燃温度进行分析。根据相关理论建立RVM煤自燃预测模型，同时和SVM、RBF模型对比。试验结果证明：SVM、RBF具有“过拟合”问题，泛化能力不高；而采用RVM预测煤自燃的方法泛化能力强、预测精度高、模型更稀疏、预测误差小等优势。