融合邻域搜索策略蚁群算法求解带时间窗口的车辆路径问题

张 雄,潘大志,2

(1.西华师范大学数学与信息学院,四川 南充 637009; 2.西华师范大学计算方法与应用研究所,四川 南充 637009)

0 引 言

车辆路径问题(Vehicle Routing Problem，VRP)，最早由Dantzig等人[1]于1959年提出，指的是多台运输车辆从配送中心出发向多个顾客运送货物，最后返回配送中心。Solomon[2]于1987年将时间窗口引入到车辆路径问题中，提出了带时间窗口的车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)，配送中心有一个时间窗口，所有车辆对顾客的送货服务必须在这个时间段内，每个顾客也设有时间窗口，车辆必须在时间窗口内才能对顾客开始服务。若车辆到达顾客的时间早于顾客最早开始服务时间，那么车辆必须等到顾客的最早开始服务时间才能服务；若车辆到达的顾客时间晚于顾客最晚开始服务时间，那么此顾客不能被这辆车服务，这种窗口称为硬时间窗口(Hard Time Window)。

对于求解VRPTW，通常采用启发式算法进行求解，因为当数据规模比较大时，精确算法需要较长的时间，对计算机的内存要求也更高。启发式算法不仅能对小规模VRPTW进行有效求解，也能对大规模问题进行有效求解，因此国内外学者对启发式算法求解VRPTW问题的研究较多如遗传算法[3-5]、蚁群算法[6]、模拟退火算法[7,8]、粒子群算法[9]、狼群算法[10]、蝙蝠算法[11]等。

Cordeau等人[12]将禁忌搜索算法用于求解VRPTW问题以及带时间窗口多车场车辆路径问题(Multi Depot Vehicle Routing Problem with Time Windows, MDVRPTW)，该算法运行速度较快，能够适应多种VRP问题；仪孝展[13]将遗传算法与模拟退火算法相结合，以防止陷入局部最优解，提高了算法的运算效率；黄务兰等人[14]提出了遗传算法与大规模邻域搜索算法的混合算法，相比传统遗传算法能够有效避免早熟，但算法运行速度较慢；Harzi等人[15]提出了一种变邻域搜索算法用于求解VRPTW问题；Paraskevopoulos等人[16]将禁忌搜索算法与变邻域搜索算法相结合求解VRPTW问题；Dong等人[17]提出了一种基于MOEA的三细胞组织P系统(PDVA)来解决多目标VRPTW问题；Alzaqebah等人[18]将蜂群算法用于求解VRPTW问题。

蚁群算法(Ant Colony Optimization, ACO)由Dorigo等人[19]于1996年提出，许多国内外学者将蚁群算法用于求解VRPTW问题，徐廷学等人[20]将量子计算融入蚁群算法；邓丽娟等人[21]将精英蚂蚁算法与变领域搜索算法融合用于求解多目标VRPTW；李奕颖等人[22]提出了基于Spark平台的改进蚁群算法求解VRPTW,该算法求解大规模问题的精度与速度有明显提升；Júnior等人[23]为提高蚁群算法的搜索性能结合变邻下降算法进行局部搜索；金淳等人[24]提出了一种改进的分布式多agent蚁群算法，该算法在精度、速度、可靠性以及求解大规模问题方面具有明显优势。

本文针对VRPTW提出一种改进的蚁群算法，在状态转移规则中引入等待时间这一因素，并且对目前最优个体进行邻域搜索，最后通过对Solomon标准测试集进行测试，验证了算法的有效性。

1 带时间窗口的车辆路径问题

VRPTW问题描述：配送中心有一定数量车型相同的运输车，在满足约束条件的情况下，安排合理的路径向顾客提供服务，使成本最低，成本包括车辆雇佣成本、运输燃油消耗成本。

1.1 基本假设

1)只有一个配送中心，车辆从配送中心出发，对顾客进行服务，最后返回配送中心。

2)已知配送中心、顾客位置、配送中心和顾客时间窗口、顾客货物需求量以及车辆最大装载量、行驶速度。

3)所有客户仅能被一辆运输车提供服务。

4)运输车辆对顾客提供服务必须在顾客规定的时间窗口内，可以早于最早规定服务时间，但不能晚于最晚规定服务时间。

5)每辆车所服务客户的总需求量不能超过车辆的最大装载量，并且车辆在提供服务时必须在配送中心的工作时间窗口之内。

1.2 数学模型

VRPTW有2个目标：使用车辆总数尽可能少和总的运输距离尽可能的短。在日常物流运输中雇佣运输司机的成本远远大于车辆行驶途中燃油消耗以及车辆磨损所带来的成本，因此将车辆使用总数为第一优化目标，总的运输距离为第二优化目标，通过加权将多目标问题转化为单目标问题。

目标函数为：

(1)

约束条件为：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

其中，公式(1)通过加权的方式将所用车辆数量和总的行驶距离这一多目标问题转化为单目标问题，并且以前者为第一优化目标。公式(2)和公式(3)表示一个顾客只能被一辆车服务。公式(4)和公式(5)表示配送中心的车辆不必全部参与运输。公式(6)表示一辆车的路径不会出现子回路。公式(7)表示离开节点的时间约束。公式(8)和公式(9)为车辆的时间窗口约束，公式(10)为车辆的装载量约束。

2 改进的蚁群算法

2.1 编码

本文采用整数编码，配送中心编码为1，顾客节点编码为2,3,4,…,N+1。假设有10个顾客需要服务，一条可行解编码为[1,3,4,8,1,7,5,2,1,6,9,11,1]，这条编码表示有3条子路径，分别为1→3→4→8→1、1→7→5→2→1、1→6→9→11→1。

2.2 候选集的构造

因为车辆有装载量的限制，顾客有时间窗限制，则候选集中的节点必须满足以下约束：

li+tij≤LTj

(11)

li+tij+wj+sj+tj1≤LT1

(12)

loadi+qj≤Q

(13)

其中，loadi为车辆在节点i当前的装载量；公式(11)为顾客的时间窗口约束；公式(12)为车辆服务时间的限制，必须在服务下一节点后能够返回配送中心；公式(13)为车辆装载量限制。

2.3 状态转移规则设计

由于时间窗口的约束，车辆在对客户i服务时会有等待时间wi(wi≥0),为使每辆车服务的客户节点尽可能多，引入等待时间，构建新的状态转移规则，如公式(14):

农村配电网线路中存在同杆并架线路时，当某回线路上发生短路故障后，继电保护将故障线路跳开，但同杆并架的另一回线路仍然处于正常运行状态。此时，由于非故障线路与故障线路间的电容和互感，导致故障点电弧电流无法降低至0，增加电弧灭弧难度。在此状态下，故障点电弧中流过的电流称为潜供电流。由于潜供电流增加了故障点灭弧的难度，延长了故障点灭弧时间，可能导致自动重合闸后故障点绝缘未成功恢复，引发重合闸失败。

(14)

(15)

2.4 蚁群算法信息素更新

(16)

(17)

(18)

其中，Q为信息素总量,ρ为信息素挥发率。

2.5 可行路径邻域搜索

由于蚁群算法易过早收敛，因此本文加入邻域搜索操作。文献[25]提出了节点移除——插入邻域搜索算子，本文在文献[25]的基础上结合VRPTW问题特征设计多种搜索算子，搜索算子包含顾客节点移除和重新插入操作，搜索算子的区别主要在于顾客节点的移除操作。

1)随机节点移除操作move_rand。

从100个客户节点中随机选择q个节点，本文设q=10，即总顾客数的10%。将选择的q个节点从路径中移除，并保存移除后的路径。

2)最长距离节点移除操作move_arc。

记Disti=distr,i+disti,j,r为节点i的前驱节点，j为节点i的后继节点，disti,j为i和j节点的距离，移除Dist最大的节点。移除操作如图1所示，从可行路径中移除6号节点，此操作是为了减少路径的总长度。

图1 节点移除操作

3)车辆服务最少顾客节点移除操作move_nodes。

选出可行路径中车辆服务顾客数最少的子路径，将所在子路径中的节点移除，此操作可减少运输车辆的使用数量。

4)节点重新插入操作insert。

将移除操作得到的节点，依次插入路径中，采用贪心的思想保存总成本最小的路径作为最终路径。由于时间窗口以及运输车装载量的约束，经过移除-插入操作可能会产生不可行解，但只需对重新插入节点的子路径进行检测修复。

5)子路径检测修复操作。

即对插入节点的路径，逐一计算每个节点的车辆开始服务时间以及车辆的当前装载量，若有不满足时间窗口或装载量约束的节点j，便将原路径从节点j截断，节点j之前的路径作为已检测过的满足约束的路径，剩下路径继续从节点j开始检验，直到所有节点都检测完成且满足约束条件。邻域搜索算法步骤为：

Step1初始化参数counter←0。

Step2对蚁群算法得到的当前种群最优路径随机选取一种节点移除操作，记录移除的节点nodes_r及路径rout_r。

Step3将nodes_r，通过insert插入算子插入到路径rout_r中，得到新路径，对新路径进行修复操作。

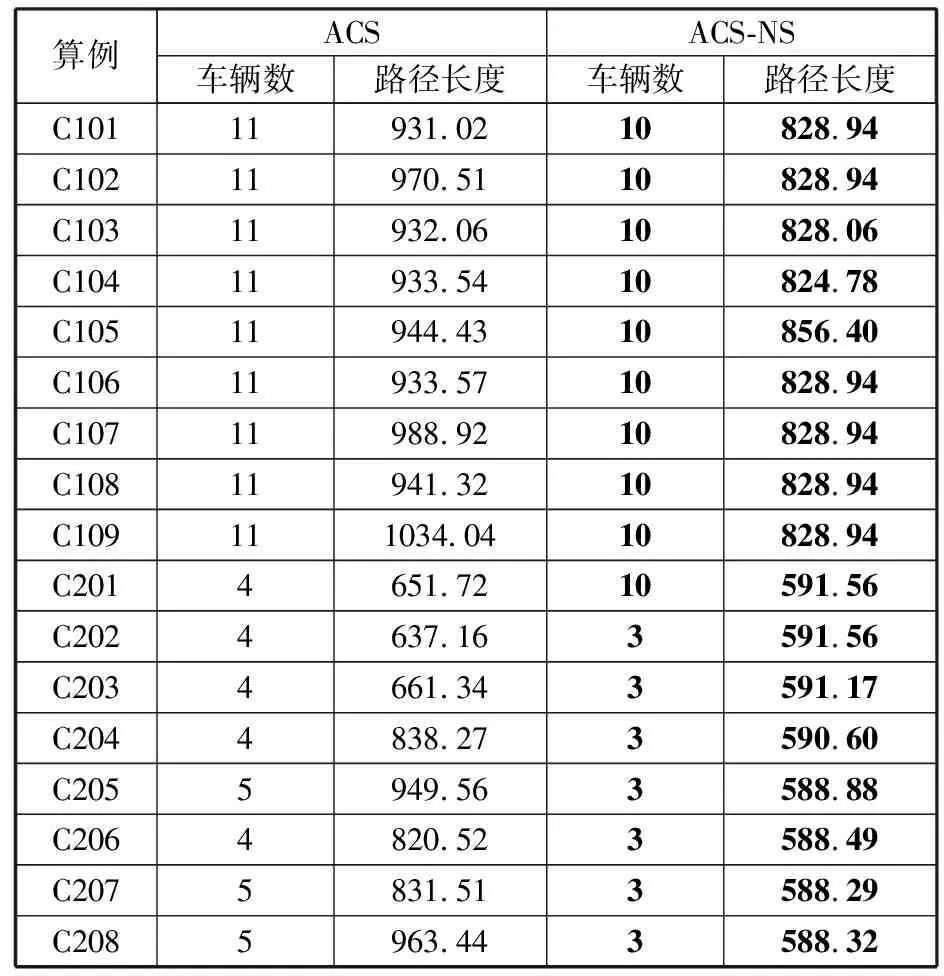
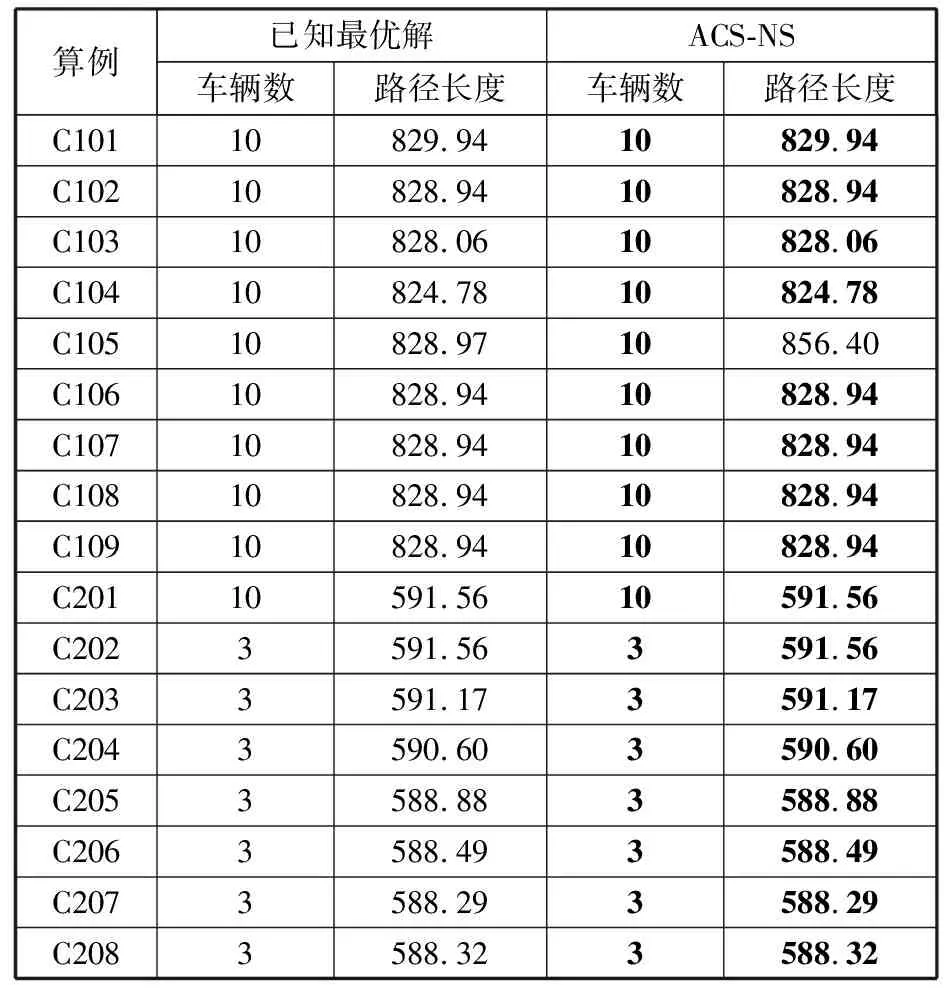
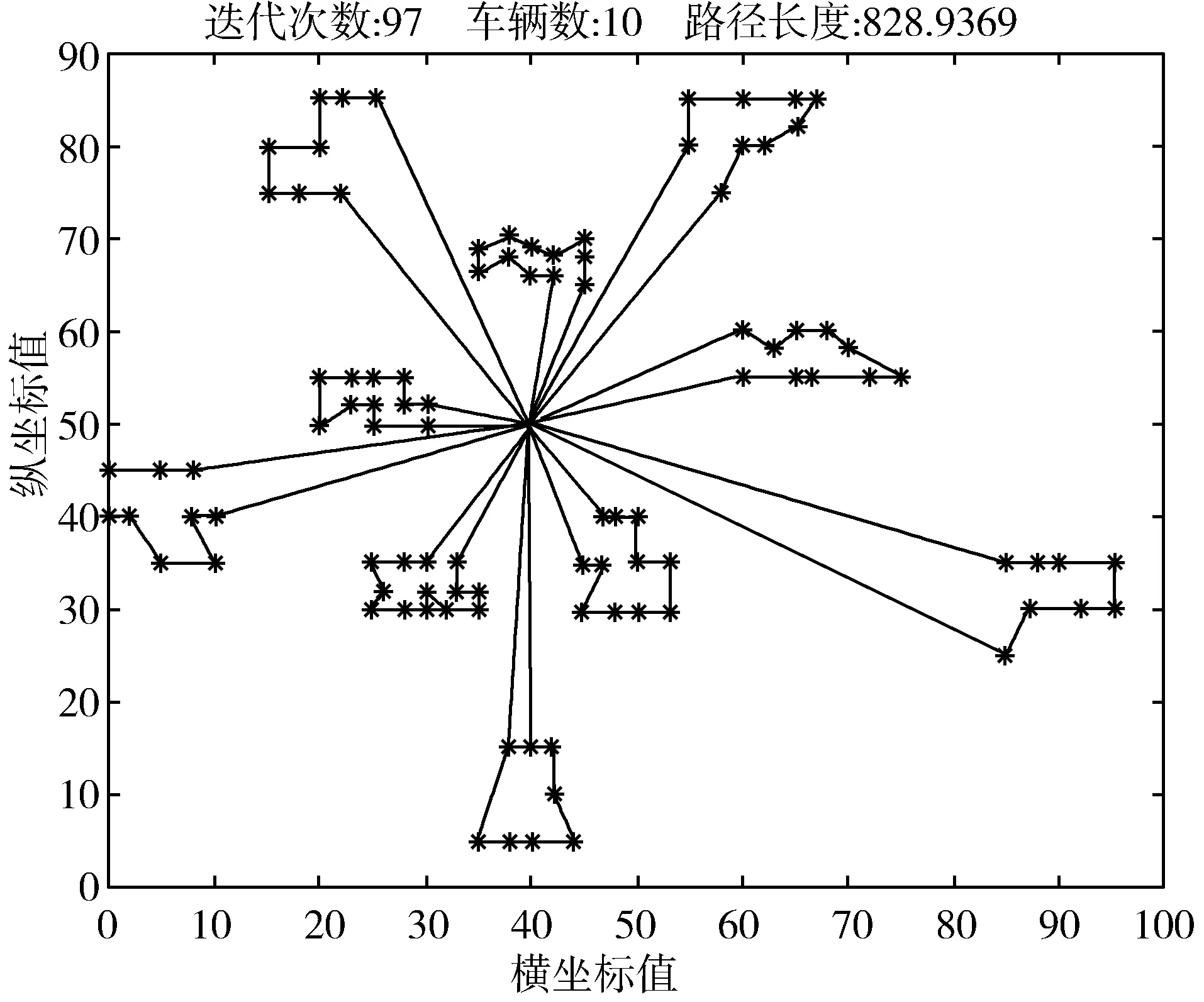
Step4counter←counter+1，若counter

2.6 算法步骤

Step1蚁群算法参数初始化,Iter←0。

Step2通过状态转移规则构造pop_size(种群大小)个路径。

Step3对当前蚁群算法得到的最优路径进行邻域搜索操作产生新路径。

Step4蚁群算法得到的种群与邻域得到的新种群按适应度从小到大排序，选取前pop_size个个体得到新种群。

Step6信息素更新，令Iter←Iter+1，更新全局最优解以及画出当前最优路径图。

Step7若Iter

3 实验分析

实验所使用计算机配置为3.5 GHz CPU、8 GB RAM、64位操作系统；编程语言为MATLAB语言,版本为MATLAB r2018a;运行参数为popsize=30，α=2,β=1.5,γ=1，ρ=0.95,Q=10，以Solomon标准测试集C类为参考，测试集中客户节点为100，包含大时间窗口与小时间窗口,车辆装载量也有大小。每种算法运行10次,最大迭代次数为400。表1～表3分别为基本蚁群算法(ACS)、文献[4]算法以及目前已知最优解与本文算法(ACS-NS)的求解结果对比。图2～图4分别为C103、C106、C204、C207算例通过本文算法所得到路径图。

表1 基本蚁群算法与本文算法结果对比

表2 文献[4]算法与本文算法结果对比

表3 已知最优解与本文算法结果对比

图2 C103路径图

图3 C106路径图

图4 C204路径图

图5 C207路径图

由表1可以看出，无论是在车辆使用数量还是路径总长度，ACS-NS算法均优于ACS算法。表2为文献[4]算法与ACS-NS算法的求解结果对比，虽然C105算例在路径总长度上ACS-NS算法求解结果要差于文献[4]算法,但误差仅为1.8%,其余算例ACS-NS算法得到的结果均优于文献[4]算法。表3为ACS-NS算法求解结果与目前最优解(http://w.cba.neu.edu/～msolomon/heuristi.htm)对比，除C105外其余算例均达到最优解，C105算例中车辆行驶距离差异为3%。通过实验分析可知改进后的蚁群算法对带时间窗口车辆路径问题有较好的适用性，能有效求解带时间窗口车辆路径问题。

4 结束语

针对带时间窗口车辆路径问题，本文提出的改进蚁群算法在状态转移规则中引入等待时间，通过构造节点移除算子(move_rand、move_arc、move_nodes)以及节点插入算子insert对蚁群算法得到的路径邻域搜索。通过Solomon算例仿真运算，运算结果与最优解对比表明改进算法能够有效求解带时间窗口车辆路径问题。