Design and analysis of shift robot with passive joint①
ZHAO Jing(赵 京), DUAN Yaxing, ZHANG Ziqiang②, XIE Biyun
(*College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124,P.R.China)
(**Department of Electrical and Computer Engineering University of Kentucky, Lexington 40506, USA)
Abstract In order to improve the efficiency of gear shifter testing, a kind of shift robot with a special passive joint is proposed to complete the human-like shifting operation automatically. The shift robot is mainly composed of two prismatic pairs, a cylindrical pair and a passive joint. The two prismatic pairs act as actuators of the mechanism to complete a part of the shifting operation,and then the shift lever can be pulled into the accurate gear position by the shift torque of the gear shifter. However,the shifting lever may skip the target gear position into the next gear position. In order to solve the gear-skip phenomenon, a limit block is applied to the passive joint. Then, the shifting processes are simulated through the dynamic model of the shift robot. The optimal position of the limit block is determined based on its dynamic characteristics.
Key words: shift robot, shifting operation, passive joint, dynamic model, gear shifter
0 Introduction
Nowadays, with the development of the automobile industry, the automobile system has been perfected, and the requirements of customers for automobiles have gradually shifted to driving comfort. The gear shifter is one of the most frequently operated automotive components. The quality of the gear shifting operation directly affects the driving experience of users. The main parameters affecting the shift quality of automobiles are shift displacement and shift effort[1-2], so the testing of shift effort and displacement is particularly important in manufacturing processes.
In order to evaluate the performance of the gear shifter, Ref.[3] obtained the information of the gear shifting force by establishing the dynamic model of it and verified it through ADAMS software. Refs[4,5]measured the shift force by manually operating the gear shifter. They analyzed the data measured by sensors,and the feeling of manual operation to qualify the shifter. The former method needs to establish dynamic models of the shifter, and the measurement process is long and complicated; the latter method is more widely used, but there is also a problem of the long test period. In order to reduce the test period, Ref.[6] proposed a shifting mechanical arm to complete the shifting process automatically. Ref.[7] developed a shifter detection system based on a three-axis industrial robot.Ref.[8] proposed an unmanned robot for testing automotive. They realized the automatic shifting operation through a seven-link mechanism which has two DOF(degree of freedom). However, all of them realize the shifting process through the active mechanism. The active mechanism relies on the actuator to move the shift lever to the target position. The testing equipment with only actuators can not achieve accurate shifting operation because the shifting displacement should be measured in the test. In order to solve this problem, a shift robot with passive joints is proposed.
Due to the underactuated characteristics of the passive joint, the mechanism can passively complete the shifting process according to the shifting force of the shifter. The passive joints are mostly used in manipulators and walking robots[9-11]. Ref.[12] proposed a multi-DOF manipulator with passive joints. The measuring tool of manipulators can move along the surface of the object relying on passive joints. Then, the shape of the objects can be accurately measured. Ref.[13] applied passive joints to an upper-limb rehabilitation exoskeleton. They used the kinematic model to calculate the displacement of joints. The result of the displacement calculation proved the adaptability of the passive joint to the glenohumeral joint. But the underactuated characteristics of the passive joint will increase the control difficulty. Ref.[14] proposed a drift suppression control method to limit the motion of passive joint in a manipulator with passive middle joint. Ref.[15] analyzed the dynamics characteristic of a biomimetic fish with a compliant passive joint. They used the dynamics characteristic in the optimization design and took control of the compliant passive joint. They completed the structure optimization and controller design by using the dynamics characteristic of the compliant passive joint. In order to control the passive joint, the dynamics of shift robot should be studied.
In order to accurately measure the shift displacement of each gear of the shifter, a shift robot with passive joint is proposed in this paper. The passive joints endow the robot with underactuated characteristics.This feature enables the robot to automatically complete a half part of the shift process under the shift torque.In this process, the shift displacement can be measured. This paper is outlined as follow. Section 1 studies the gear shifter model. Based on the analysis of the gear shifter, the configuration synthesis of the shift robot is completed. The working principle of the shifting robot is illustrated at the end of this section. In Section 2, the kinematics model of the shift robot with the passive joint is deduced. Subsequently, the Lagrange method is used to establish the dynamic model of the robot. In Section 3, the mechanical structures of the active actuator and passive joint in the robot are introduced. In Section 4, the robot dynamics model and ADAMS software are used to simulate the four shifting processes. The results of the ADAMS simulation verifies the correctness of the dynamic model. Finally,based on the dynamic characteristics of the shifting robot, the position of the limit block on the passive joint was determined.
1 Mechanism design
1.1 Mechanism of shift robot
Fig.1(a) is the gear shifter needed to be tested,and there are five gears along the PRNDS direction in Fig.1(a). These gears are P (Parking), R (Reverse), N(Neutral), D(Drive) and S(Sport) gears.When the shifter lever is in the D gear, it can be switched to the M gear in the direction of the arrow.Fig.1(b) is the internal structure of the gear shifter.As can be seen from the figure, the shifter has two rotatory DOF. Therefore, the gear shifter can be simplified as a ball pin pair.

Fig.1 Gear shifter
The shifter testing robot needs to have two functions, shift torque measuring and shift displacement measuring. In order to achieve this goal,the shift robot must be able to achieve the shifting operation. The closed-loop mechanism of the shifting robot and the gear shifter needs to have two DOF due to the two rotatory DOF of the gear shifter. According to the above design requirements, designs the first generation of shifter testing robot is proposed as shown in Fig.2(a).The mechanism is composed of six links, two prismatic pairs, two rotatory pairs, a cylindrical pair, and a ball pin pair. By using Kutzbach-Grubler equation, the DOF of the mechanism can be obtained as follows.

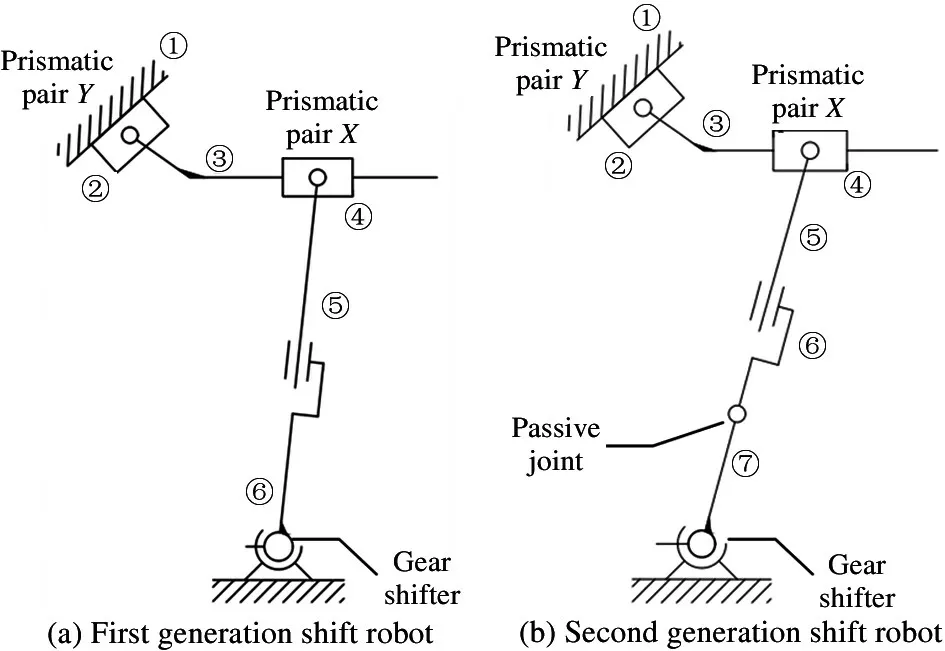
Fig.2 Mechanism of shift robots
From research on shift torque in Ref.[3], it can be found that in the process of shifting, shift torque will change from resistance torque to dynamic torque.According to this characteristic, a kind of shift robot with a passive joint is designed[17]. Based on the firstgeneration shift robot, a passive joint is applied between the shift lever and the cylindrical pair. By utilizing the characteristics of the underactuated system,the shift lever slides automatically to the target gear position under the shift torque. The degree of freedom of the mechanism is calculated as follows.
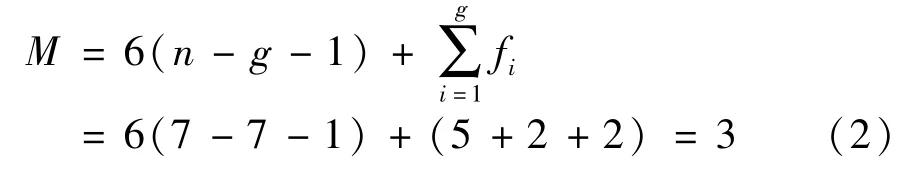
1.2 The shifting process
In shifting operation, people first actively pull the shift lever to a certain angle, and then shift lever will automatically slide to the gear position following the shift torque. Therefore, the shifting process of the mechanism is divided into two parts, the active process and the passive process according to the shifting operation of humans. The special passive joint is shown in Fig.3(c) and (d). The shift robot can realize the human-like shifting operation through the different posture of the passive joint. In the active process, Link 2 will contact the self-lock block under the drive of prismatic pair X. Then the passive joint is locked as shown in Fig.3(c), the shift lever will be sent to the middle position under position control. In this process, shift torque changes from resistance torque to dynamic torque. After the active process is completed,the actuators will be locked, and the robot becomes a planar four-bar mechanism shown in Fig.3(b). At this moment, the shift torque is the dynamic torque acting on the shift lever. As shown in Fig.3(d), Link 2 will leave the self-lock block. In this way, the shift lever will automatically reach the precise gear position driven by the shift torque. It should be noted that the shift moment is an uncontrollable driving source in the passive process, and the mechanism is underactuated. If the shift torque is too large, the shift lever will skip the target gear and slide to the next gear, which is defined as the gear-skip phenomenon. In order to solve the gear-skip, a limit block is applied to the passive joint.If the position of the limit block is appropriately designed, the Link 2 will collide with it when gear-skip occurs. Then the shift lever can move backward to the target gear position. The position of the limit block will be discussed in Section 4.
2 The kinematic and dynamic model
2.1 The active process
The shift robot divides the shifting process into two stages. In the active process, the mechanism is a spatial two-degree-of-freedom mechanism shown in Fig.4,in which the shift lever is driven by two prismatic pairs and pulled to the middle angle. After determining the middle angle, it is necessary to study the kinematics model of the mechanism in the active process. The mapping relationship between the displacement of actuators and the angle of shift lever can be found through the kinematic model. The displacement can be used in position control of the robot.
As shown in Fig.4(a) and (b), the Cartesian coordinate origin is at the center of the shift lever rotation. Choose the displacementxandyof the prismatic pairs as independent variables. The kinematics model of the mechanism in Eq.(3) can be obtained through the simple geometric relationship. Then the middle angle of the lever is substituted into the inverse kinematics model. The displacement of the prismatic pair in each shifting process can be calculated.


Fig.4 Mechanism of the robot in the active process and passive process
2.2 The passive process
During the passive process, the actuators do not work, and the passive joint is in a free state. The mechanism changes to a planar four-bar mechanism,as shown in Fig.4(c). Under the driving of shift torque,the shift lever slides spontaneously to the gear position.However, the shift robot in the passive process is not a traditional four-bar mechanism. The mechanism does not adopt a simple position control strategy but relies on unknown shift torque as its driving source. The state of the mechanism can not be predicted only by its kinematic model. So in order to obtain the motion characteristics of the mechanism in the passive process, it is necessary to establish the dynamic model of the system.
According to the simplified model of the mechanism (Fig.4(c)),AB′C′Dis its initial configuration,and 4B′C′Dis its configuration at a particular moment in the passive process. Choosing the angleφ1of the shift lever as the generalized coordinate of the system,the kinematics model (Eq.(4)) of the passive process can be derived from the geometric relationship between links.

wherel1,l2, andl3are the lengths of Link 1, Link 2,and Link 3.His the height from the two prismatic pairs to the ground.φ0is the initial angle ofφ1.The values of these parameters are listed in Table 1.
Chooses theXYplane as the zero potential surface of the system, andφ1as the generalized coordinate,then the Lagrange function of the mechanism in theAB′C′Dstate is as follows.
Now deep in this forest, as the stepmother well knew, there was a green lawn and on the lawn stood a miserable little hut on hens legs, where lived a certain Baba Yaga, an old witch grandmother. She lived alone and none dared go near the hut, for she ate people as one eats chickens. The merchant s wife sent Vasilissa into the forest each day, hoping she might meet the old witch and be devoured15; but always the girl came home safe and sound, because the little doll showed her where the bush, the flowers and the berries grew, and did not let her go near the hut that stood on hens legs. And each time the stepmother hated her more and more because she came to no harm.

where

3 Structure design
3.1 Joint design
According to the previous analysis, the mechanism has two DOF in the active process. At this time,the two prismatic pairs of theXaxis andYaxis are used as its actuators, and the partial shifting process is realized by position control. The two actuators of the shift robot have the same mechanical structure shown in Fig.5(a). The rotating shaft of the stepping motor is connected with the ball screw pair, and the screw nut is fixed with the slider. When the motor rotates, the slider can move in a straight line along the axis of the screw.

Fig.5 The mechanical structure of actuators and passive joint
The passive joint is the critical component of shift robot to realize shift displacement measurement. By applying two pins to the passive joint, the self-locking block and the limiting block mentioned above can be realized. The contact strip applied on the Link 2 can touch the block to realize the function of the passive joint. Fig.5(b) shows the mechanical structure of the passive joint. In the active process, there is a decreasing trend of ∠ABCdriven by actuators. When ∠ABC=180 °, the contact between the contact strip and the self-lock block of the passive joint causes the lock of the passive joint; While in passive process, driven by the shift torque, ∠ABCshows a growing trend, and the contact strip will break away from the self-lock block, making the passive joint free.
3.2 Size synthesizing
In the shift robot shown in Fig.4(c), Link 1 is the shift lever whose length is determined. According to the kinematics analysis of the passive process in Section 2, the relationship between the length of Link 2 and Link 3 needs to satisfy Eq.(4). Therefore, after determining the heightHof the robot,the size synthesis of the mechanism can be accomplished only by solving the maximum sum of the lengths of Link 2 and 3 in the range of the reachable lever angle. The shift robot is designed based on the length and structure appearing above. Table 1 shows the structural parameters of the whole machine and the physical parameters of the critical components.
4 Dynamic analysis and gear-skip solution
The shifter has five gears,which are P,R,N,D,and S gears. So the shift robot needs to complete four shifting processes: PR, RN, ND, and DS, and measure their shift displacement and torque. However, in the process of the experiment, gear-skip appears in the ND shifting process, which causes the shift lever to slide over the D gear and fall into the S gear. Gearskip occurs in the passive process. In order to find the solution of gear-skip, the motion characteristics of the shift robot system in the passive process should be analyzed. Therefore, this section will analyze the dynamic characteristics of the system based on the dynamic model established in Section 2. And seek the solution of dynamic analysis.
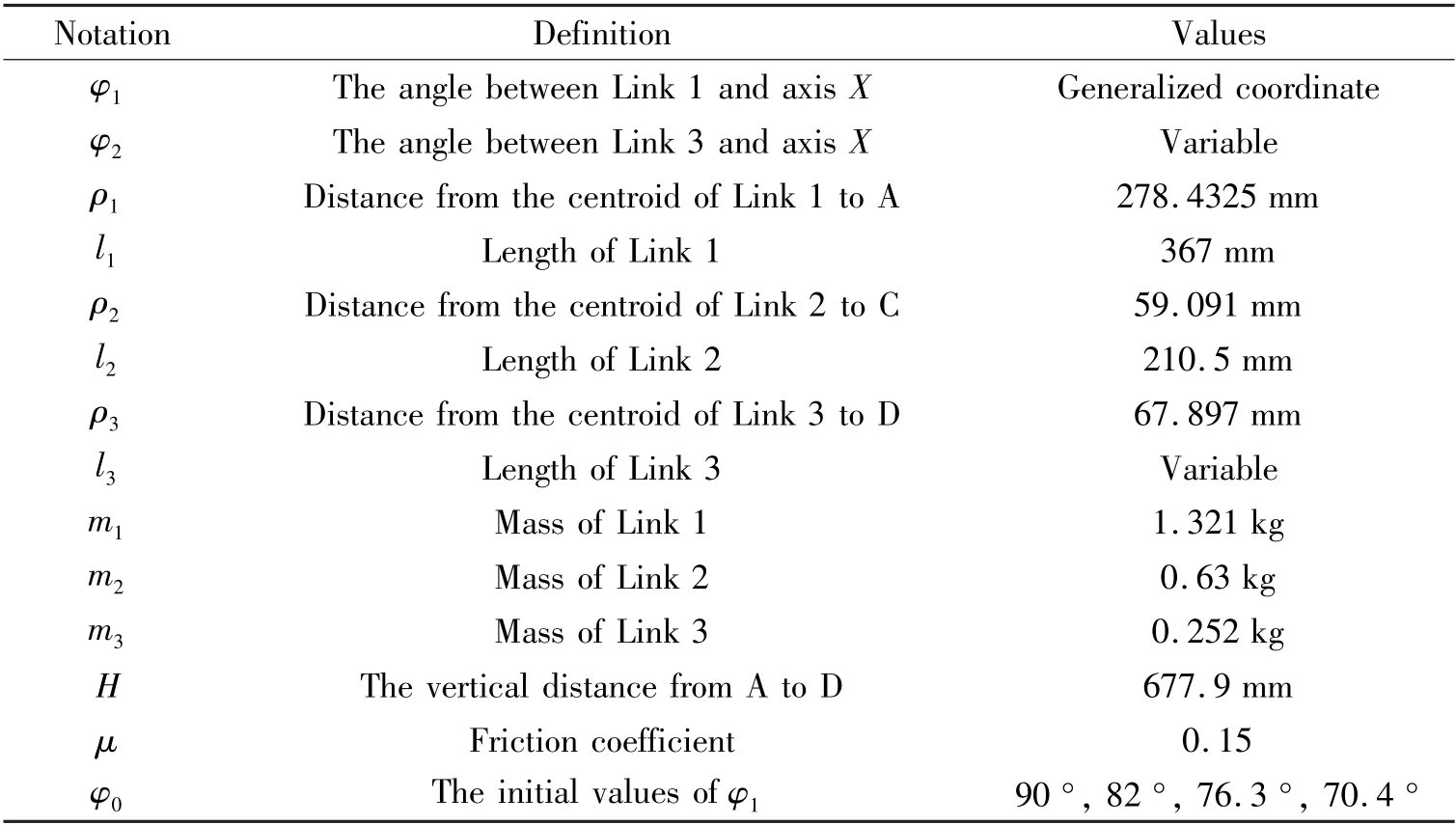
Table 1 Parameters of robot
4.1 Dynamic analysis and simulation
From the dynamic equation shown in Eq.(7), it can be seen that the left of the Eq.(7) is related to the structural and physical parameters of the shift robot,and these parameters have been determined in Table 1.The right of the Eq.(7) is the generalized external force the shift torque. In order to analyze the dynamics of the system, it is necessary to calculate the shift torque. In order to analyze the dynamic characteristics of the system, it is necessary to calculate the shift torque. According to the analysis on the gear shifter in Ref.[3], there is a special tooth-shaped plate component in the gear shifter. When the ball at the end of the spring lever moves on it, the spring on the spring lever will be compressed to provide the shift torque.Therefore, the inner part of the gear shifter is simplified as the tooth-shaped plate mechanism shown in Fig.6(a). According to its mechanism, when the normal of the contact surface between the tooth-shaped plate is not collinear with the spring lever, the force acting on the spring lever will provide the shift torque.The profile of the tooth-shaped plate is obtained from engineering documents which is provided by the gear shifter manufacturer. The profile curve is discretized in Autocad software. The piecewise cubic spline function of the tooth profile can be obtained by the interpolation method.

Fig.6 Force analysis of gear shifter
One of the factors affecting the shift torque is the elastic force of spring, which is linearly related to the length of the spring lever. As shown in Fig.6(b) and(c), the end sphere with radiusris tangent to the tooth-shaped plate, and the normal equationAx+By+C= 0 can be obtained from the spline function of the tooth-shaped plate. The tangent point coordinate is defined as (a,b).At this time, the coordinates of the sphere center (Cx,Cy) can be calculated by Eq.(8).It is necessary to note that there will be an over-tangent phenomenon at some points, and these points should be deleted.
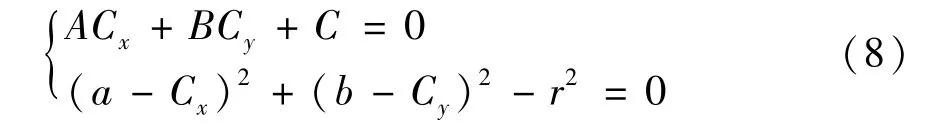
Shift torque of the shifter can be divided into three cases. In case 1, as shown in Fig.6(b), the cross product of spring lever vectorOAand normal force vectorOBof tooth plate is negative, then the normal force of the tooth plate acts on the resistance torque of coordinate origin. In case 2, as shown in Fig.6(c), the cross product of spring lever vectorOAand normal force vectorOBis positive. The normal force of the tooth plate acts as the driving torque on the coordinate origin. In case 3,OAandOBare collinear, then the normal force does not provide shift torque to coordinate origin. The torque symbol of the normal force acting on the origin is related to the cross product ofOAandOB,so its transmission angle can be calculated as follows:



wherekis the spring elastic coefficient,R0is the length of the spring lever, andx0is the deformation of spring in P gear.Ris the radius of the spring lever end sphere.

Fig.7 Part of shift torque provided by the normal force
Before analyzing the dynamic characteristics of the shifting robot, it is necessary to verify the correctness of the dynamic model shown in Eq.(7). The shifting robot is simplified and shown in Fig.9. This simplified model can be imported into the ADAMS software to simulate the four shifting processes. The simulation results can be used to verify the dynamic model of the shifting robot. In the simplified model, the mass of each component is concentrated at the centroid of mass,and the parameters of link length,mass,and position of the centroid are consistent with the theoretical calculation. In the process of building the simulation model,the friction forces at each joint are ignored.
According to the analysis of the shift torque, the shift torque is generated by the spring force and the friction force. These two forces are related to the contact between the spring rod and the tooth-shaped plate.However, when setting contact constraints in the ADAMS software, the relevant parameters of the constraints are difficult to determine, and the model with contact constraints is difficult to be solved. As can be seen from Eq.(10), the shift torque is a function ofφ1.Therefore, the discrete shift torque can be obtained by Eq.(10). Then contact constraints can be implemented by applying the discrete shift torque to the shift lever.

Fig.9 The motion process in simulation
It should be noted that in the ADAMS simulation,the GSTIFF solver with the I3 integral format is used to simulate the shifting process of the shift robot. The accuracy of the solver is 1E-6, and the simulation step size is 0.001 s. The simulation results of four shifting processes are shown as the dashed line in Fig.8. The final stability values of the shift lever angles in each process are close to the theoretical values, and the error is no more than 0.2 °. Compared with the theoretical calculation result, the simulation curves show the same characteristics as the theoretical calculation, and the gear-skip appears in the ND process. These characteristics prove the validity of the dynamic model established by the Lagrange method.
4.2 Conditions about avoiding gear-skip
In order to find a solution to the gear-skip, it is necessary to consider the influence of the shift robot on the shifting process. Similar to the dynamic analysis process of the shift robot system, the dynamic model of gear shifter is established in the Eq.(11) by Lagrange method, the four values ofφ0in Table 1 are taken as the initial value of solving the differential equation,and the result is obtainbed as shown in Fig.10. It can be seen from the figure that the shift lever can arrive at the target gear after a period of oscillation. This experimental result just proves the relationship between the gear-skip and shift robot.
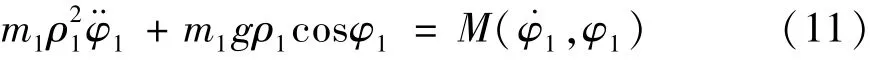
It can be drawn from the results of theoretical calculation and simulation that the gear-skip only occurs in the ND shifting process. The reason is that the total mechanical energy of the system increases after the involvement of the shift robot. The friction between the tooth-shaped plate and the spring lever can not completely consume the potential energy difference between the two middle gears, so the residual kinetic energy drives the shift lever sliding to the D gear.

Fig.10 The shift lever angle curve without the shift robot
In order to make the shift robot adapt to the shifter better, a limit block is applied to the passive joint to avoid the gear-skip. When the passive joint angle∠ABC=φ2-φ1+180°reaches a specific limit, the active bar will collide with the limit block. This limit of the passive joint angle will limit the oscillation range of the shift lever angle. In this way,the gear-skip is avoided. The position of the limit block needs to satisfy two conditions. One is that it can collide in the ND shifting process. The other is that it can not hinder other shifting processes, and Link 2 can not contact the limit block in PR, RN, and DS shifting processes as far as possible. In the ND shifting process, the angular speeds of˙φ1and˙φ2satisfy the relationship of Eq.(12)after Link 2 collides with the passive joint. The material of the passive joint in the shift robot prototype is steel, and the approximate recovery coefficient of the steel is 0.55.

Then the angular velocity of the shift lever after the collision can be calculated by combining with Eq.(4). Fig.11 shows the shift lever angle curves after applying the limit block at different positions. In the figure, The circle point is the collision point, and the square point is the stable point. The stable timeTshows a decreasing trend from Fig.11(a) to (g),which means that the closer limit block is to the target position, the faster the system can be stabilized. However, it should be noted that the phenomenon of secondary collision appears in Fig.11(e) - (g), which will shorten the service life of the machine. Therefore,the secondary collision can be regarded as a constraint and the best position to apply the limit block on 71.5 °is obtained.

Fig.11 The shift lever angle curves under applying limit block
5 Conclusion
A shift robot with a passive joint is proposed. The passive joint is designed according to the dynamic characteristics of shift robot. The conclusions are as follows.
(1) A three DOF shift robot with a passive joint is proposed. The shift robot uses the characteristics of the shift torque and the passive joint to solve the problem that the active shift mechanism cannot achieve accurate shifting operation. Therefore, the shift robot can accurately measure the shift torque and displacement.
(2) By studying the dynamic characteristics of the shift robot, the cause of the gear-skip phenomenon is found. A limit block is applied to the passive joint to prevent the gear-skip occurrence, and its position is determined according to the dynamic characteristics of the shifting robot.
 High Technology Letters2022年1期
High Technology Letters2022年1期
- High Technology Letters的其它文章
- Deep convolutional adversarial graph autoencoder using positive pointwise mutual information for graph embedding①
- A joint optimization scheme of resource allocation in downlink NOMA with statistical channel state information①
- Personalized movie recommendation method based on ensemble learning①
- An improved micro-expression recognition algorithm of 3D convolutional neural network①
- Resonance analysis of single DOF parameter-varying system of magnetic-liquid double suspension bearing①
- Computation offloading and resource allocation for UAV-assisted IoT based on blockchain and mobile edge computing①
