Spar风电平台涡激运动特性研究

宋佳奇，王俊荣，2，王德志，康信龙

(1.中国海洋大学 工程学院，山东 青岛 266100;2.山东省海洋工程重点实验室，山东 青岛 266100)

海洋风能资源丰富、风场稳定，海上风能资源开发已成为未来新能源开发的热点。Spar风电平台具有水线面小、重心低等特点，因此拥有优良的运动性能和稳性是开发深海风能的重要装备。

由于Spar风电平台吃水较深，在海流作用下会导致其后方产生交替脱落的旋涡，从而形成顺流向和横流向的脉动压力，使平台产生大幅的水平运动，称之为涡激运动(Vortex-Induced Motion，VIM)。Spar风电平台一般为无侧板单立柱平台，该种平台形式更易发生大幅涡激运动。Hywind Scotland Spar型6MW风电平台是立柱直径14.4 m、吃水78 m 的无侧板单立柱Spar风电平台，该类平台在实际运行中易监测到显著的大幅涡激运动[1]。涡激运动对系泊系统的疲劳带来挑战，需对其运动现象及规律进行深入研究。

目前，海洋平台涡激运动的主要研究方法有实尺度观测、模型试验和计算流体动力学(Computational Fluid Dynamics，CFD)数值计算等，其中计算流体动力学数值计算方法具有可操作性强、易重复和耗费少等优点，已逐步成为涡激运动的主要研究方法。2005年Thiagarajan等[2]采用计算流体动力学数值计算方法计算对比了有、无侧板圆柱的涡激运动频域特点;2014年苏云龙[3]对单根圆柱固定绕流进行了计算流体动力学数值计算，通过流场分析研究了旋涡脱落机理，但未考虑流固耦合;2015年赵伟文和万德成[4]用计算流体动力学数值计算方法计算了Ur为5～9时有侧板Spar平台的涡激运动响应，并与模型试验进行了比较;2016年Duan 等[5]采用模型试验的方法研究了OC3 Spar型浮式风机的涡激运动特性，发现并分析了平台横荡、纵荡锁频现象;2018年翟佳伟等[6]研究了风浪流联合作用下Spar基础的运动特性，其涡激力由二维圆柱绕流计算流体动力学数值计算模型计算得到;2019年何佳伟等[7]计算模型尺度下的有、无侧板Spar平台的涡激运动过程，重点关注了螺旋侧板的减涡效果。针对无螺旋侧板Spar风电平台，获取平台涡激运动响应幅值与来流约化速度关系曲线，是分析平台涡激运动特性和评估系泊系统疲劳的基础。

本文建立了无侧板单立柱Spar风电平台二维计算流体动力学数值计算模型，开展平台在不同流速下的涡激运动数值计算，探究Re不相似对平台涡激运动的影响，为平台相关设计分析与试验提供参考。

1 数值方法

1.1 控制方程

涡激运动是非定常、黏性流问题，本文假设流体为不可压缩牛顿流体，采用雷诺平均法(Reynolds Average Navier-Stockes，RANS)处理纳维-斯托克斯方程(N-S方程)，得到的控制方程包括:

1)连续方程

2)动量方程

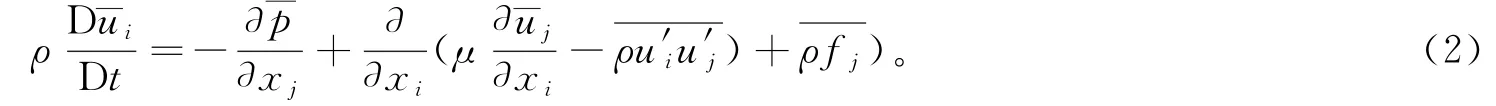
1.2 湍流模型

本文所使用SSTk-ω湍流模型是一种雷诺平均法，最早由Menter等[8-9]提出。该模型通过剪切应力输运(Shear Stress Transport，SST)过程将k-ω模型和k-ε模型两湍流模型结合，在近壁面区域采用边界条件处理能力良好的k-ω模型，在远场采用自由剪切流处理较好的k-ε模型。SSTk-ω模型充分结合k-ω模型kε模型的优点，提高了计算精度。模型中湍动能(k)和特定湍流耗散率(ω)方程分别为[8]:

式中:μt为湍流涡动力黏性;νt为湍流涡运动黏性;P为湍流生成项;为进行限制后的生成项;β*为修正系数;β，γ，σk和σω均为封闭参数;F1为混合函数，用以在近壁处激活标准k-ω模型，在远场处激活k-ε模型;CDkw(cross-diffusion)为交叉扩散项。式(3)和式(4)右侧前3项分别为生成项、耗散项和扩散项，式(4)右侧第4项为交叉扩散项。其中:

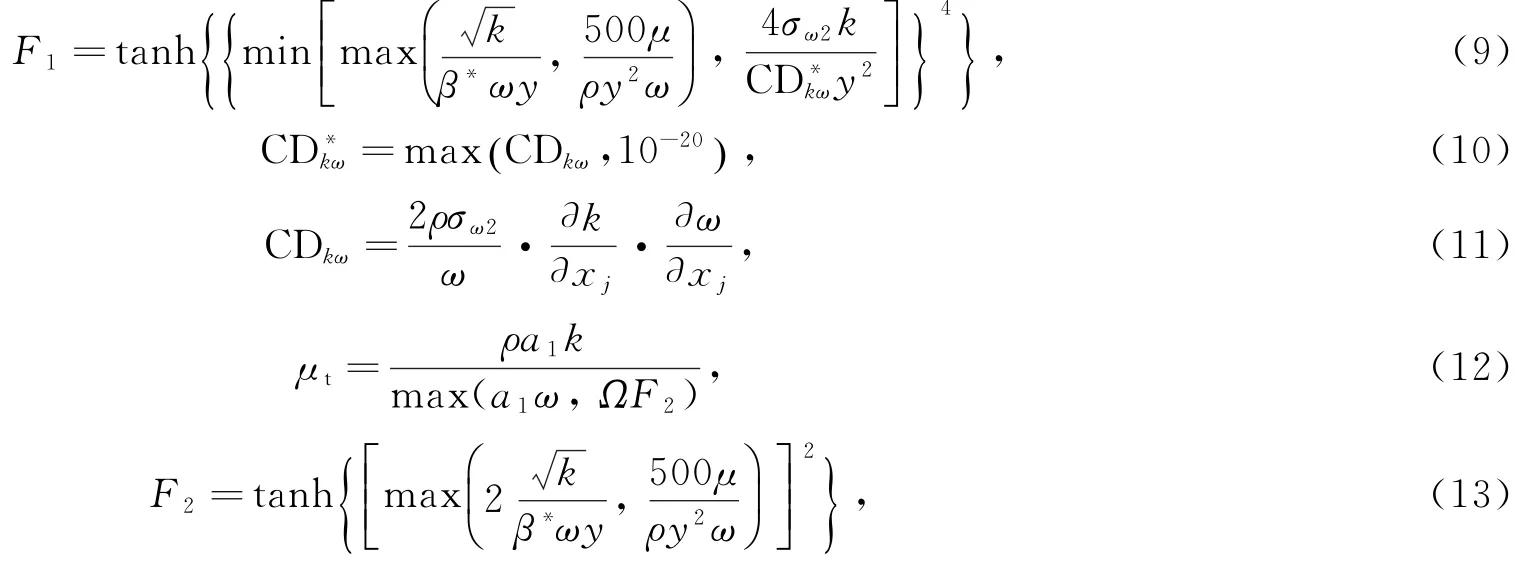
式中:S ij为平均应力张量;δij为克罗内克函数;CD*kω为修正后的交叉扩散项;Ω为旋度幅度;y为距最近壁面距离;a1为修正系数;F2为混合函数;封闭参数β、γ、σk和σω在近壁处和远场处具有不同值，下标1为近壁处参数值，下标2为远场处参数值，其中各参数值为0.5，β1=0.075、σk2=1.0、σω2=0.856、β2=0.028、β*=0.09、κ=0.41、a1=0.31。β、β*、γ、σk和σω在距离面不同位置具有不同的值，须加权平均得到式(3)和式(4)中的值，对任意参数α，有:

1.3 流固耦合

计算物体流固耦合运动需要采用动网格技术，对于平台大幅度往复运动的问题，重叠网格方法可实现多个相互独立网格之间产生无拘束相对运动，网格不变形，可稳定地进行流固耦合计算。通过自编程序计算物体运动的动力积分，实现对重叠网格的运动控制和流固耦合。具体做法是:在每一时间步内，将计算流体动力学数值计算求解得到的流体激励代入平台运动微分方程求解物体运动响应，然后对重叠网格位置及流场进行更新，完成该时间步的流固耦合，流程见图1。

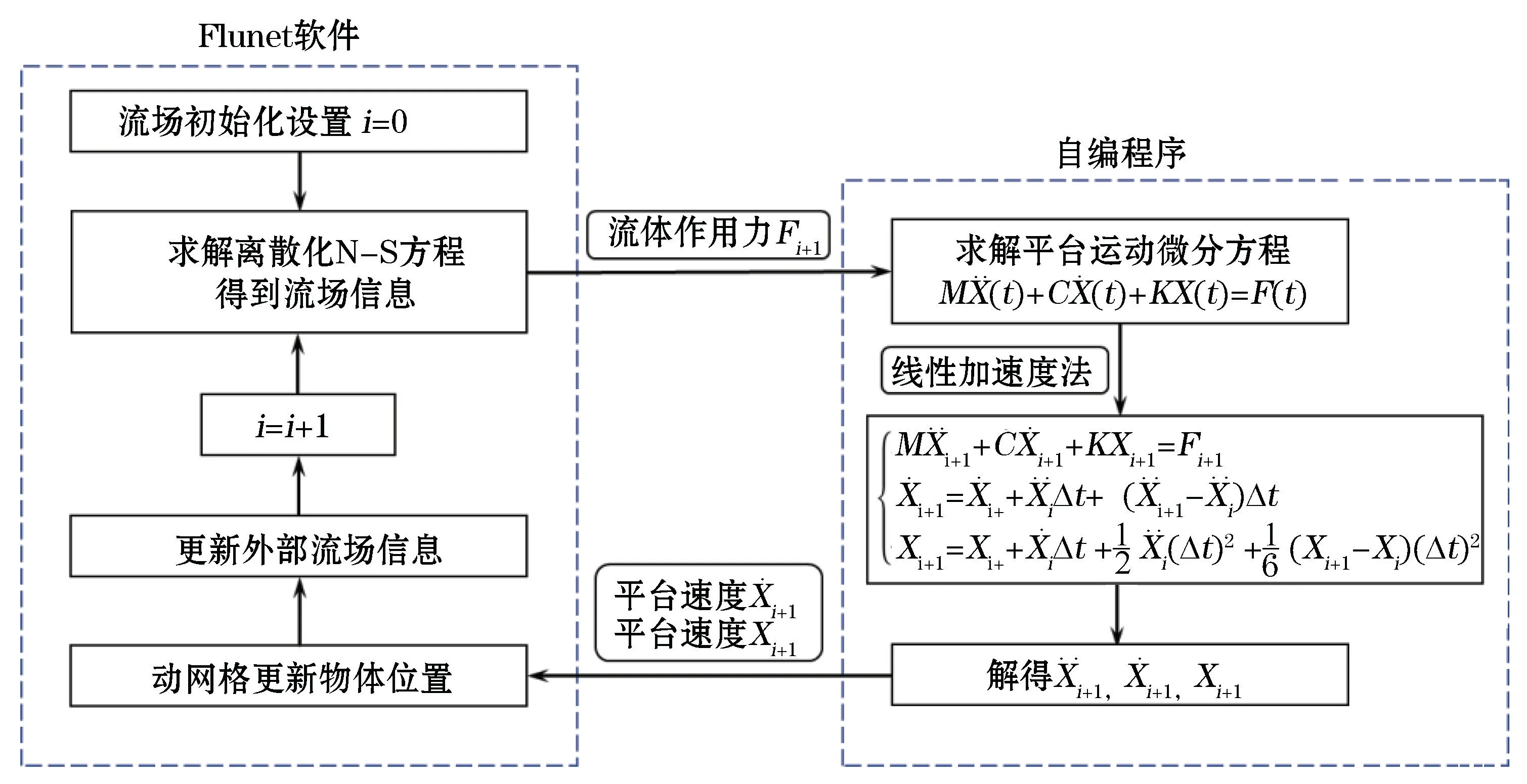
图1 涡激运动流固耦合求解流程Fig.1 Flow chart of solving the VIM fluid-solid coupling

1.4 涡激运动相关特征参数

本文重点关注如下浮式平台涡激运动无因次参数:

式(15)～式(20)中:St为斯特劳哈尔数;A/D为无量纲振幅，其中D为结构特征长度(立柱直径)，A为平台运动幅值;CL为升力系数，CD为阻力系数，采用阻力系数均值和升力系数标准差(CL′)来表征平台水动力系数;ρ为流体密度;U为来流速度;fv为平台涡脱频率;fn为平台静水横荡频率;Xmax和Xmin分别为平台顺流方向偏移最大值和最小值;F Y和F X分别为水动力在横流向和顺流向的分量;SL和SD分别为浸没部分向升力和阻力方向的投影长度。

2 计算模型及工况

2.1 平台模型

本文重点研究Spar风电平台在海流作用下的涡激运动响应特征，不考虑空气引起的涡激运动。实际尺度下，Spar风电平台立柱直径为10 m，吃水120 m，质量8 450 t。因涡激运动响应主要表现在水平面内运动，立柱截面不变，兼顾计算效率问题，故采用平台二维涡激运动模型进行涡激运动计算。在计算流体动力学数值计算时采用1∶50的缩尺比，通过在计算流体动力学数值计算中定义流体黏度，可满足雷诺数Re相似准则。

2.2 系泊系统

平台模型采用等效线性水平系泊提供回复力，系泊系统由4根线性弹簧组成，布置方式如图2所示，平台立柱中心为坐标系原点，每根弹簧与坐标轴的夹角为45°，平台横荡、纵荡固有周期相等，实际尺度下，系泊刚度为2×104N/m，预张力为1.5×106N;系泊系统整体的阻尼比为0.06。

图2 平台系泊方式示意图Fig.2 Sketch map of the mooring mode of the platform

2.3 计算区域、边界条件与网格划分

计算区域分为背景网格和前景网格两部分(图3)，背景网格为矩形区域，以平台立柱直径D为基准，矩形长36D，宽16D;前景网格为正方形区域，边长7D。为保证有足够空间使流场中旋涡充分发展，背景网格中平台设置在靠近流体入口的一侧，平台中心距左侧流体入口处8D。

图3 计算区域几何简图Fig.3 Geometry diagram of the computational domain

计算区域边界条件设置左侧为速度入口边界;右侧为压力出口边界，给定出口静压力p=0，对流动中的其他物理量均由流场内部值外差得到;上下边界设置为自由滑移壁面;平台立柱表面为无滑移壁面边界，边界上流体速度与壁面速度相同;前景网格边界设置为重叠网格边界。

对于湍流模型参数，k和ω的初始流场和入口边界条件可以通过经验公式计算得到[9]，即

式中:I为湍流强度，νt/ν为湍流黏度与层流黏度之比。在无滑移壁面边界处，k和ω的法向梯度为0，，其中y1为壁面第一层网格单元中心到壁面距离。

为研究网格收敛性，选取3种不同密度网格进行网格测试，网格设置见表1所示。当Re=1.42×104时，计算3套网格的和St，在保证计算结果稳定的前提下，时间步长取Δt=0.02 s，结果如表1所示。网格2与网格3计算结果接近，继续加密网格对精度提高的效果有限，故采用网格2进行后续数值计算，网格划分如图4所示。

图4 计算区域整体网格划分Fig.4 Grid division of the entire computational domain

表1 不同网格计算结果Table 1 Results calculated based on the different sets of grids

3 计算结果与分析

3.1 固定绕流计算

为了验证数值计算方法的可靠性，首先对平台固定绕流进行数值计算研究，本文选取4个工况，对平台受力计算结果进行统计分析，工况设置及统计各工况结果所得的St及如表2。将本文计算所得的St同Blevins[10]总结的St-Re关系曲线、苏云龙[3]数值计算的St结果对比(图5)，本文及苏云龙计算得到的St均略高于Blevins所得St-Re关系曲线;将本文计算所得的同Schlichting[11]所得关系曲线、苏云龙[3]数值计算的结果对比(图6)，其数值接近Schlichting所得关系曲线。本文数值模型计算结果处于合理范围。

图5 斯特劳哈尔数与雷诺数的关系Fig.5 Relationship between the Strouhal number and the Reynolds number

图6 阻力系数均值与雷诺数的关系Fig.6 Relationship between the mean of drag coefficient and the Reynolds number

表2 平台绕流工况及统计结果Table 2 Conditions and statistics of the flow around the Spar

3.2 涡激运动计算

本文探究平台在Ur=2～14范围内的涡激运动规律，计算模型与原型满足Re相似准则，流体动力黏度μ=2.837×10-6Pa·s，此时平台横荡和纵荡的固有频率fn=0.086 Hz，称该平台系统为系统1，具体工况设置如表3所示。

表3 系统1涡激运动计算工况Table 3 Conditions for VIM calculation of System 1

图7为各工况平台纵荡、横荡运动时历曲线及平台运动轨迹图。对比图7中不同Ur下平台的运动轨迹，得到平台运动的变化特点和规律:Ur=2时，平台运动轨迹呈“8”字形，但幅值较小;Ur=3 时，运动轨迹开始发散;Ur=4时，平台运动轨迹总体呈现出“C”字形的运动轨迹，横荡、纵荡幅值均较大;Ur=7时，平台运动轨迹变为狭长的“8”字形，横荡幅值较大，纵荡幅值较小;Ur=10 时，平台运动轨迹开始发散，运动轨迹变为在一定范围内的往复运动;Ur＞10时，平台运动范围大幅缩小，横荡、纵荡幅值均明显减小。

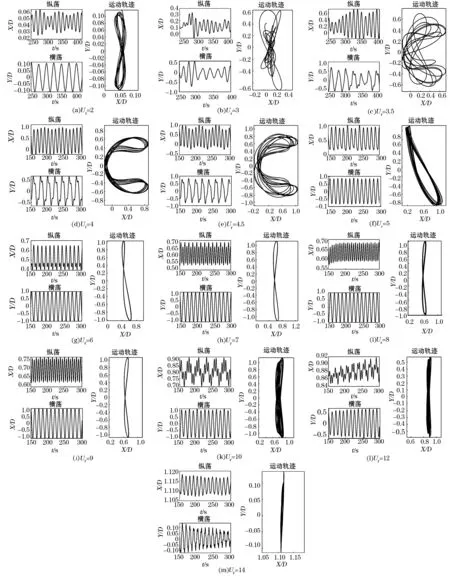
图7 不同约化速度下纵荡、横荡运动时历曲线及运动轨迹Fig.7 Time history and trajectory of the surge and sway motions at different reduced velocities

通过对平台CL时历曲线做傅里叶变换，得到各工况下旋涡脱落频率(fv)。图8为Spar风电平台不同Ur下的横荡频率(fsway)、涡激运动涡脱频率(fv-VIM)和根据Blevins[10]总结的St计算得到的固定绕流涡脱频率(fv-Blevins)对比图。由图8可见，在Ur=3.5～10范围内，fv-VIM与fsway几乎一致，且与fv-Blevins相差较大。fv-VIM出现了2次频率锁定现象:在Ur=3.5～4.5时，平台发生了纵荡共振，此时为纵荡锁频，fv-VIM为0.048 Hz，纵向激励力振荡频率与平台纵荡固有频率相近;在Ur=5～10时，平台发生了横荡共振，此时为横荡锁频，fv-VIM为0.085 Hz，横向激励力振荡频率与平台横荡固有频率相近。U r=10时fv-VIM和fsway开始出现差别，Ur＞10时fv-VIM明显高于fsway，接近于fv-Blevins。

图8 横荡频率、涡激运动涡脱频率和固定绕流涡脱频率Fig.8 A contrast map of f sway，f v-VIM and f v-Blevins

对各工况结果进行统计分析，得到图9所示的不同Ur下平台纵荡和横荡运动特征参数对比。图9中X和Y为平台纵荡、横荡偏移平均值，平台纵荡、横荡运动幅值A X和A Y可由最大值减去均值近似计算得到。结合图8和图9可知:在纵荡锁频时A X和Xmax显著变大，Ur=4.5时A X达到最大;在横荡锁频时A Y/D＞1。锁频现象显著影响平台涡激运动幅值，平台设计时应考虑纵荡锁频对平台运动响应的影响。

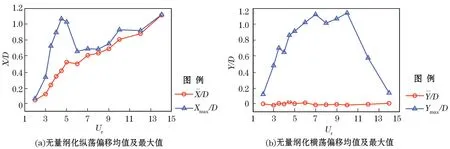
图9 无量纲化平台纵荡、横荡运动的均值和最大值Fig.9 Nondimensionalized mean and maximum of the surge and sway motions at different reduced velocities

3.3 不满足雷诺相似准则的影响

物理水池试验无法满足Re相似准则，实验结果与原型运动结果会产生差异，本节通过计算流体动力学数值计算方法探究不满足雷诺相似准则对涡激运动计算结果的影响。设置计算模型的流体动力黏度为1.003×10-3Pa·s，平台系统横荡、纵荡固有频率为0.084 Hz，称此平台为系统2(表4)。

表4 系统2工况设置表Table 4 Condition settings for VIM calculation of System 2

图10 2个系统阻力系数均值和升力系数标准差对比Fig.10 Comparison of and C′L between the two systems

图11 相同约化速度下系统1和系统2平台运动轨迹对比Fig.11 Comparison of Spar motion trajectory between System 1and System 2 at the same reduced velocity

4 结 论

本文采用计算流体动力学数值计算方法对一无侧板单立柱Spar风电平台涡激运动现象进行数值计算，研究平台在不同Ur的涡激运动特征。计算采用SSTk-ω湍流模型，通过自编动力积分程序和重叠网格实现涡激运动的实时流固耦合，对平台在Ur=2～14的涡激运动响应进行了计算，分析了涡激运动模式随Ur变化的规律，定性分析了不满足雷诺相似准则对涡激运动计算的影响。得出以下结论:

1)平台在不同Ur下会经历2次锁频，在Ur=3.5～4.5时出现运动轨迹呈“C”字形的纵荡锁频，在Ur=5～10出现运动轨迹呈“8”字形的横荡锁频。

2)获取了平台纵荡和横荡无量纲振幅曲线，发现锁频现象对涡激运动响应幅值影响明显。

3)物理模型试验因无法满足Re相似，高估了黏性力，在横荡锁频时高估了顺流向的运动幅值，低估了横流向的涡激运动幅值。