三年级第一学期数学应用题解与析

广东佛山市南海区西樵实验小学 冯绮墁

Some maths word problems seem difficult, but they are not actually. To solve those so-called difficult word problems, you need to do some analysis on them first. After that, you need to choose the right strategies and use some skills to solve them step by step.

Let’s take the following word problems as examples to analyze and solve them one by one.

Example 1:

In the garden, there are 48 red flowers. The yellow flowers are 3 times as many as the red flowers. There are 25 more purple flowers than yellow flowers. How many yellow flowers are there in the garden? How many purple flowers are there in the garden?

This word problem asks us two questions, which are “How many yellow flowers are there in the garden?” and “How many purple flowers are there in the garden?”

For the first question, we need to find out the numbers of the yellow flowers.

It is known that “The yellow flowers are 3 times as many as the red flowers.” That’s to say, if there was only 1 red flower in the garden, there would be 3 yellow flowers in the garden, as the yellow flowers are 3 times as many as the red flowers.

We can make a table below.

?

We also know that there are 48 red flowers, so we may do the calculation by multiplying 48 and 3, and write the equation sentence of multiplication as the below:

The word problem also tells us that there are 25 more purple flowers than yellow flowers. It means that the purple flowers are more than the yellow flowers. How many purple flowers are more than the yellow flowers? 25. So, to find the number of the purple flowers, we can add 25 and 144.

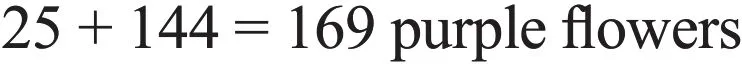
By the way, if this word problem asks us one more question“how many flowers are there in the garden in total?” what will you do next? Yes, as there are three kinds of flowers in the garden,which are red, yellow and purple, we may add up them to find the sum.

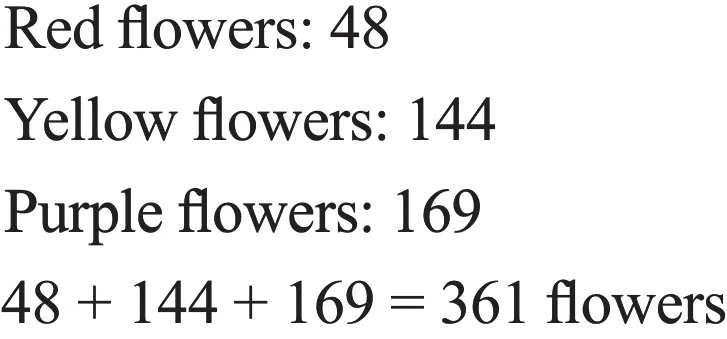
Example 2:

The bag of rice is heavier than the bag of salt. The difference in weight between the bag of rice and the bag of salt is 2 kg 200 g.The bag of salt is 800 g. What’s the weight of the bag of rice?

This word problem is easier than the word problem in Example 1. What do we know about this word problem?

a. Here is a bag of rice and a bag of salt.

b. The bag of rice is heavier than the bag of salt.

c. The difference in weight between the bag of rice and the bag of salt is 2kg200g.

d. The bag of salt is 800g.

e. It asks us what’s the weight of the bag of rice.

As the difference in weight between the bag of rice and the bag of salt is 2kg200gand the bag of salt is 800g, it actually tells us about the following:

the weight of the rice – the weight of the salt = 2kg200g

the weight of the rice – 800g= 2kg200g

As “a – b = c” can be turned into “a = b + c”, the equation sentence “the weight of the rice – 800g= 2kg200g” can be turned into the following:

the weight of the rice = 2kg200g+ 800g

As 2kg200gcan be converted to be 2kg+ 200g, we may write:

the weight of the rice = 2kg+ 200g+ 800g

the weight of the rice = 2kg+ 1000g

As 1000gis equal to 1kg, we may write:

the weight of the rice = 2kg+ 1kg

the weight of the rice = 3kg

Example 3:

Here is a storybook. There are 246 pages in the storybook. If Jim reads 9 pages each day, in how many days will he finish reading the storybook?

This word problem seems very easy, but some of the students fail to do it correctly. Why? Because they are careless!

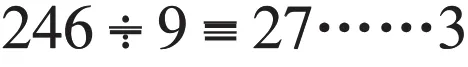
As the quotient is 27 with the remainder 3, some of the students would simply write an answer “27” or an answer “27……3”. However, neither of the two answers is correct! Because in 27 days, Jim can only finish reading 243 pages of the book while another 3 pages are not read!

The correct answer is “28 days”!

Example 4:

There are fewer than 20 candies on the table. If the candies are divided equally among 3 children, 1 candy will be left; if the candies are divided equally among 5 children, also 1 candy will be left. How many candies are there on the table?

This word problem seems very hard. But never be nervous!Try to make clear what information this word problem tells us first.

a. The unknown number is fewer than 20.

b. If the unknown number is divided by 3, the remainder is 1.

c. If the unknown number is divided by 5, the remainder is 1, too.

d. It asks us what number it is.

Now we can see that we need to find the lowest common multiple (“LCM” in short) of 3 and 5 first. As “3 × 5 = 15”, 15 is the LCM of 3 and 5. This is Step 1.

What about Step 2 then? Just add 15 and the remainder 1,which is 16. And 16 is fewer than 20. Is the unknown number just 16? We can check the answer as the below:

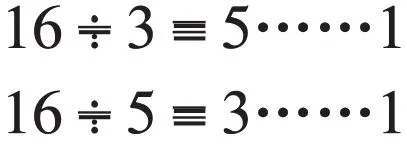
Now we can be sure of the answer “16 candies”.

Example 5:

4 same rectangles form a big square. The side length of the big square is 25 cm. Find the perimeter of each of the rectangle.

This word problem seems too hard,as it does not tell us how long the length of the rectangle is or how long the width of the rectangle is. It only tells us the length of the square is 25cm. How can we find the perimeter of each of the rectangle?

Actually, we can! Why? Use your mind and think it over.

Think about the following first:

a. To find the perimeter of a rectangle, what do we need to know? Yes, we need to know the length and the width, as the formula of rectangle’s perimeter is “(length + width) × 2”.

b. What does 25cmmean? It means the length of the square.Yes, it is the length of the square. But can you find anything more about 25cm? Observe the figure more carefully, and you’ll find that“25cm” is just the sum of the length and the width of the rectangle!

Now that you have known the sum of the length and the width of the rectangles, is it very easy to work out the perimeter of each of the rectangles? Yes, absolutely! We may write as the below: