基于探地雷达杂波抑制与偏移成像的树木根系定位方法

李光辉 徐 汇 刘 敏

(江南大学人工智能与计算机学院， 无锡 214122)

0 引言

根系检测是树木健康状况评价的重要手段，在古树名木和果树养护管理等方面都能发挥重要作用。现有的根系检测方法大致分为破坏性检测和无损检测[1](Non-destructive testing, NDT)两类。传统的破坏性检测方法包括根钻法、土芯法、土壤剖面法和全根挖掘法[2-3]等，这些方法劳动强度大且费时费力，不适合大规模应用，还可能对周围的根系造成不可逆转的破坏。而X射线断层扫描、核磁共振方法、声学方法和电阻率层析成像[4-8]等检测方法能够实现根系参数无损测量。探地雷达(Ground-penetrating radar, GPR)作为一种新兴的地球物理探测方法，已经被应用于树木根系和树干的无损检测[9-12]。与其它无损检测方法相比，探地雷达具有易于操作，野外便携，可以扫描大型根系并且能够快速、经济地进行重复测量等优点[13-15]。

探地雷达沿扫描路径向地下发射电磁波，通过接收到的反射回波来绘制扫描区域的地下高分辨率雷达图(B-scan图像)。但是，探地雷达B-scan图像通常会因为发射和接收天线之间的直接耦合、地表反射和非平坦地形的散射响应引起的杂波造成模糊[16]。因此，探地雷达B-scan图像应用于任何地下物体检测算法之前，必须先进行杂波抑制。最简单常用的方法是均值减法(Mean subtraction, MS)，但是目标响应的强度会受到均值减法的影响而减小。子空间方法，如奇异值分解(Singular value decomposition, SVD)、主成分分析(Principal component analysis, PCA)和独立成分分析(Independent component analysis, ICA)，将B-scan图像视为几个子空间的并集，通过去除杂波子空间来减弱杂波[17-20]。但是，子空间方法需要对杂波子空间进行精确测量和划分才能获得理想的杂波抑制效果。鲁棒主成分分析(Robust principal component analysis, RPCA)通过优化低秩和稀疏矩阵表示问题来分离杂波和目标响应，在真实数据上表现优于子空间方法[21]。

通过偏移技术对杂波抑制后的B-scan图像进行聚焦以实现目标定位。探地雷达常用的偏移算法包括后向投影算法(Back projection, BP)、克希霍夫(Kirchhoff)积分法、逆时偏移(Reverse time migration, RTM)、频率-波数域偏移(F-K偏移)[22-25]等。F-K偏移在频率-波速域中采用快速傅里叶变换(Fast Fourier transform, FFT)进行求解，相对其他3种偏移方法，具有更高的计算效率，实际应用广泛。然而偏移成像聚焦效果与偏移速度密切相关，对于点目标来说，当偏移速度与实际速度一致时，能量汇聚到同一绕射点上，偏移能够完全聚焦，如果偏移速度小于实际速度，偏移就不能完全聚焦，目标形成的双曲线不能完全消除，如果偏移速度大于实际速度，双曲线开口方向有反转的趋势。为有效利用B-scan图像定位树木根系，本文提出基于RPCA和深度自动编码器结合的杂波抑制方法，使用直接最小二乘法拟合目标回波双曲线估算介质相对介电常数求取偏移速度，最后通过改进插值的F-K偏移实现根系定位。

1 研究方法

1.1 鲁棒深度自动编码器

从数学上讲，观测到的探地雷达B-scan数据X可以由一个表示直达波等背景信号的低秩矩阵L，一个表示目标回波信号的稀疏矩阵S和一个随机噪声矩阵N联合表示[26]，即

X=L+S+N

(1)

鲁棒主成分分析利用凸优化求解式(1)。

(2)

式中 ‖·‖*——核范数

‖·‖1——l1范数

‖·‖F——F范数

λ——控制稀疏矩阵稀疏性的惩罚系数

ε——任意正数

核范数用于对矩阵的奇异值求和来获取低秩分量，RPCA用迭代奇异值的线性方法来求解核范数，l1范数用于计算矩阵元素的绝对值之和来获取稀疏分量。本文应用RPCA和深度自动编码器相结合的鲁棒深度自动编码器(Robust deep autoencoder, RDAE)来抑制探地雷达B-scan图像的杂波。典型的自动编码器是一个3层结构的神经网络。如图1所示，自动编码器由包含n个节点的输入层、h个节点的隐藏层和n个节点的输出层组成。自动编码器的目标是最小化输入数据x与输出数据x*之间的重构误差，因此可以将最小化重构误差作为自动编码器的损失函数，即

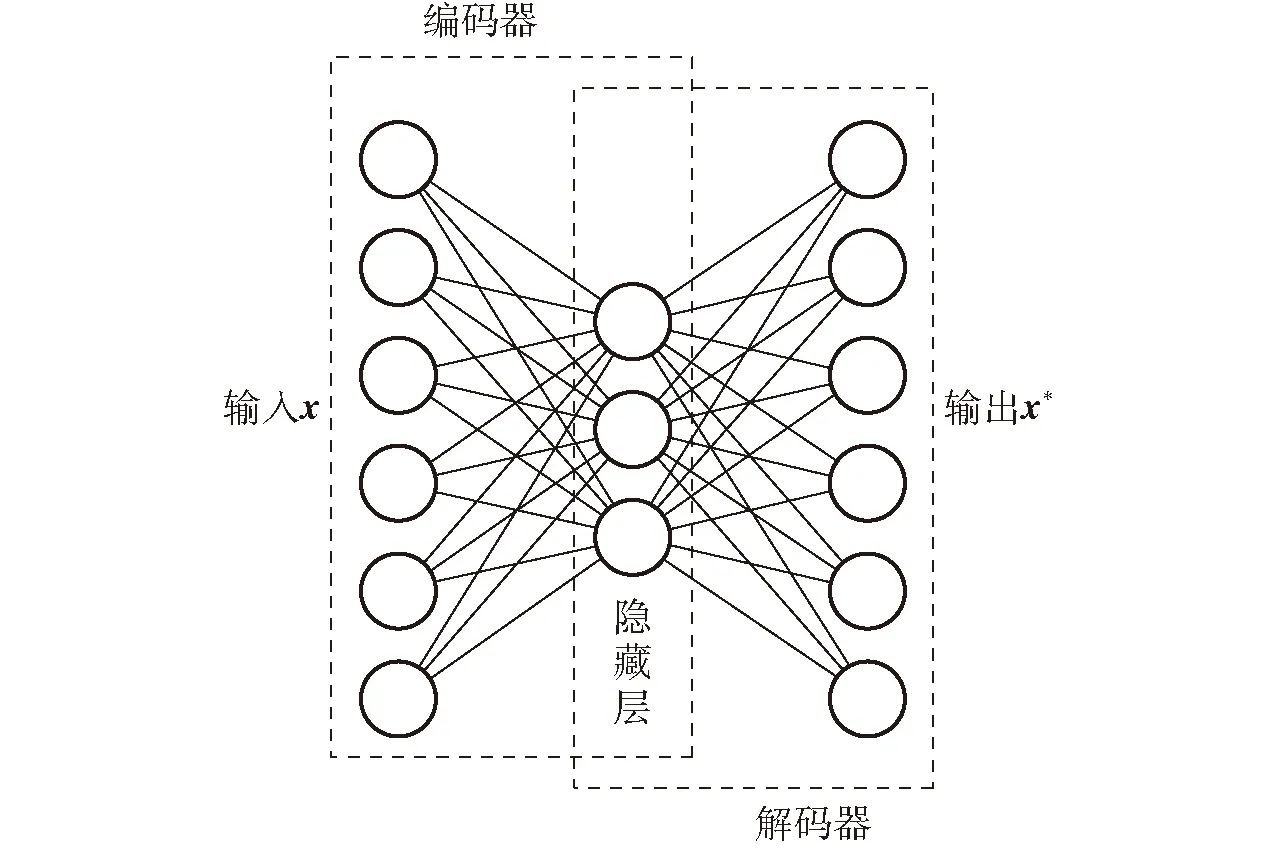
图1 自动编码器结构图Fig.1 Architecture of autoencoder

(3)

式中 ‖·‖2——l2范数

E(·)——编码器D(·)——解码器

具有多个隐藏层的自动编码器被称为深度自动编码器[27]，每增加一个隐藏层需要增加一对编码器和解码器，通过多个编码器和解码器，深度自动编码器可以有效地表示输入数据上的复杂分布。RDAE获取稀疏分量的方式类似于RPCA，采用l1范数，但是RDAE继承了深度自动编码器获取低秩分量的非线性能力，在不规则杂波条件下优于RPCA，RDAE将式(2)修改为优化问题

(4)

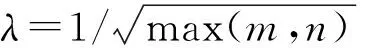
1.2 直接最小二乘法

一般地，当探地雷达天线扫描经过树根上部土壤时，树根反射雷达脉冲形成的回波双曲线可以表示为

(5)

式中x——天线位置

t——雷达波的双向传播时间

c——真空中光速

εr——土壤的相对介电常数

(x0,t0)——双曲线顶点坐标

在式(5)中，树根直径被忽略，这是可以接受的，因为本文中的树根直径比雷达波长小。土壤的相对介电常数采用直接最小二乘法(Direct least square, DLS)拟合双曲线计算[28]。相较于霍夫变换(Hough transform, HT)，DLS对不规则双曲线拟合效果更好。图2为执行DLS算法的流程图。为了说明该过程，给出了图3所示的DLS方法处理仿真B-scan图像的示例。图3a、3b为进行零点校正和杂波抑制后的B-scan图像，转为灰度图以获取联通区域，采用Canny算子提取的联通域边缘拟合图3c中标红的上边缘。在DLS循环的每次迭代中，从上边缘随机选取10个坐标点，记录每次求解的参数(x0,t0,εr)，使用DLS拟合的双曲线见图3d。本文已利用仿真数据对DLS的准确性进行了测试，该仿真涉及具有不同相对介电常数的均质土壤。在用DLS拟合双曲线的循环迭代过程中，当待拟合的点到双曲线的误差平方和(Sum of the squared errors, SSE)小于给定阈值时，终止迭代。

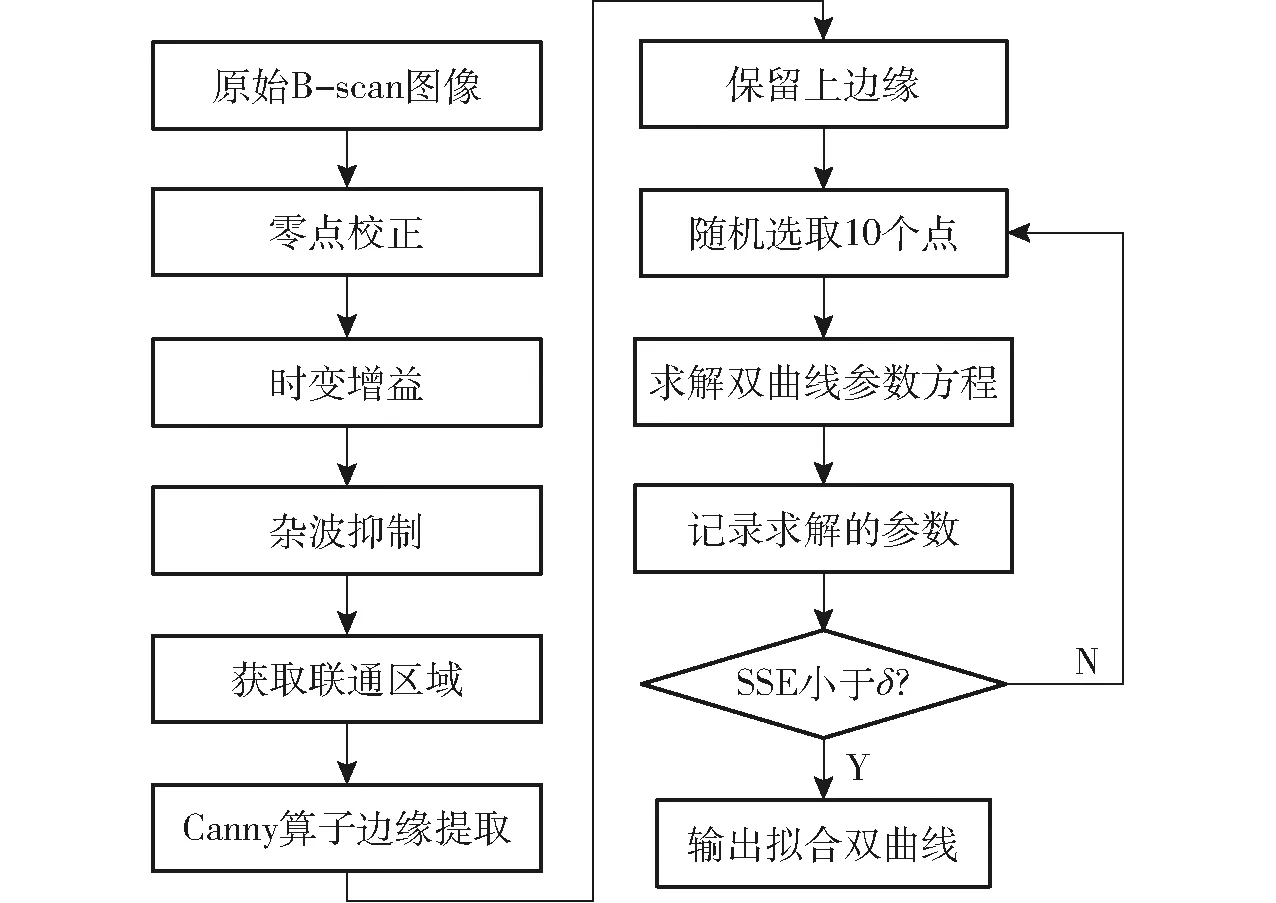
图2 基于DLS的双曲线参数估计算法流程图Fig.2 Flow chart of DLS-based algorithm for hyperbola parameter estimation

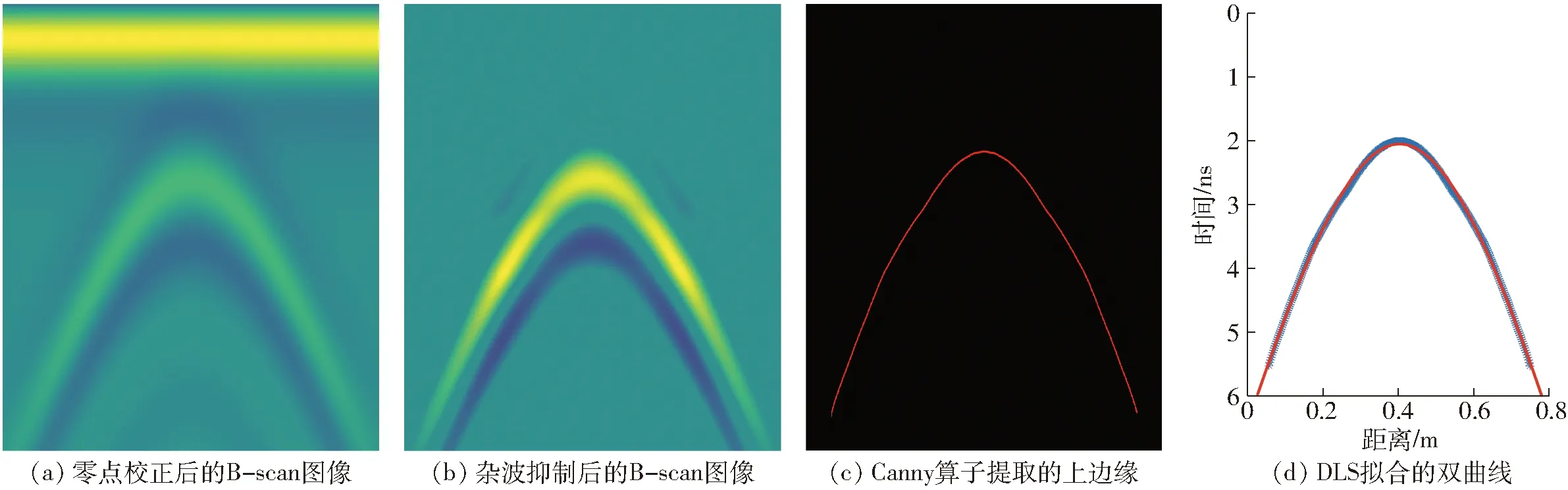
图3 基于DLS算法拟合双曲线示例Fig.3 Examples of hyperbola fitting with DLS algorithm

1.3 F-K偏移

根据惠更斯原理，如果电磁波的波前(Wavefront)在t时刻的位置是已知的，将t时刻波前上的每个点看作t+Δt时刻波前的子波源，如图4所示，t+Δt时刻的波前可由t时刻波前叠加重建。在探地雷达检测中，电磁波从空气传播进入地下界面，将地下界面的各个反射点看作子波源，对接收到的记录剖面作时间反演，即为探地雷达的偏移成像。

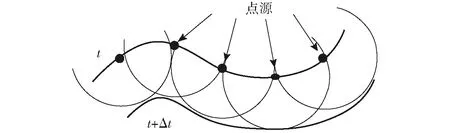
图4 惠更斯原理图Fig.4 Schematic illustration of Huygens principle

设探地雷达B-scan记录剖面为p(x,z=0,t)，z是垂直坐标，向下为正，P(kx,z=0,ω)是偏移后剖面p(x,z,t=0)的二维傅里叶变换，即

P(kx,z=0,ω)=∬p(x,z=0,t)e-j(kxx+ωt)dxdt

(6)

将式(6)在频率-波数域做波场外推，深度z处的波场可以表示为

P(kx,z,ω)=P(kx,z=0,ω)ejkzz

(7)

由于探地雷达记录电磁波的双程走时，因此可以把波速视为介质中波速v的一半，根据色散方程，kx、kz和ω的关系可以表示为

(8)

设p(x,z,t)是P(kx,z,ω)关于kz、ω的二维傅里叶逆变换，代入色散方程式(8)，同时令t=0可得偏移后的图像。

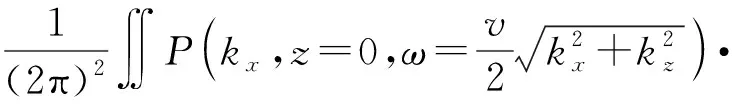
(9)

为了提高偏移图像的分辨率，在F-K偏移的实现上改进了时频插值方法[29]。首先，对杂波抑制后的B-scan数据在t方向进行零填充来提高频率域的分辨率，使得ω到kz域的插值误差减小，然后在快速傅里叶逆变换前对kx域中数据进行零填充以提高x方向上的空间采样率。改进后的F-K偏移流程如图5所示。

图5 改进的F-K偏移流程图Fig.5 Flow chart of improved F-K migration

2 实验与结果分析

2.1 实验数据采集

实测数据采集使用美国GSSI公司的SIR-3000型探地雷达，雷达天线包含400、900 MHz 2种频率，如图6所示。实验数据分成实测数据和仿真数据2组。实测场地位于江南大学西北操场沙坑，选择人工填埋的香樟粗枝代替真实根系，开展根系定位的模拟实验，检测区域的土壤类型主要为细沙，细沙材质均一，易于模拟且相对介电常数与土壤较为接近，实测实验期间未发生降雨，细沙的含水率稳定。仿真数据使用基于时域有限差分(FDTD)方法求解麦克斯韦方程的开源软件gprMax[30]获得，gprMax允许CPU并行计算，并且支持GPU加速运算。gprMax中大多数命令是可选的，但必须指定模型尺寸，空间离散化步长和时窗大小。本文实验数据处理平台搭载Intel Core(TM) i7-9700处理器，主频3.0 GHz，内存16 GB，Nvidia GTX1660显卡，6GB显存。开发环境为Matlab 2019a、Python 3.8和深度学习框架Pytorch 1.5。

图6 GSSI SIR-3000型探地雷达Fig.6 GSSI SIR-3000 model ground-penetrating radar

2.2 杂波抑制

首先使用仿真模型对提出的方法进行测试，仿真模型模拟了城市路面的分层结构，如图7所示，仿真的分层模型由15 cm厚的沥青层、15 cm厚的水泥层和50 cm深的干燥黏土组成，水泥层的粗糙上下表面高度在3 cm内变化，埋在土壤中的根系半径为4 cm，探地雷达沿扫描方向进行探测，仿真基本参数见表1。

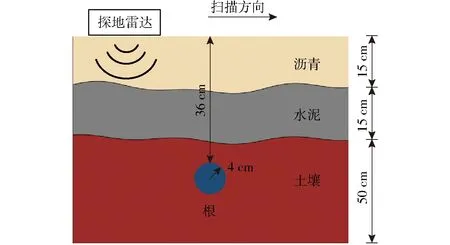
图7 城市路面结构的仿真模型Fig.7 Simulation model of urban road structure

表1 仿真基本参数Tab.1 Simulation parameters

使用改善因子(Improvement factor, IF)定量分析杂波抑制前后图像信杂比(Signal-to-cutter ratio, SCR)的改善程度，IF值越大，杂波抑制方法性能越好。IF定义为

(10)

其中，F为改善因子，Sbefore和Safter分别是应用杂波抑制方法前后B-scan图像的信杂比，信杂比定义为

(11)

式中Ns——目标信号区域Rs中的像素数

Nc——杂波区域Rc中的像素数

I(p)——B-scan图像第p个像素的信号强度

如图8所示，由于水泥层粗糙不平表面的影响，许多不均匀的杂波无法通过MS和SVD很好地与目标回波分离。RPCA和RDAE通过低秩和稀疏矩阵分解，能更好地分离杂波并保留目标回波。RDAE中深度自动编码器共包含7层，每层的节点数为512、128、32、8、32、128、512，激活函数为Sigmoid，以便深度自动编码器学习输入的非线性表示。表2给出了4种方法的IF值，去除2个最大主成分的SVD性能比MS略好，RPCA和RDAE能更好地分离目标信号与杂波，但RDAE具有更高的IF值。

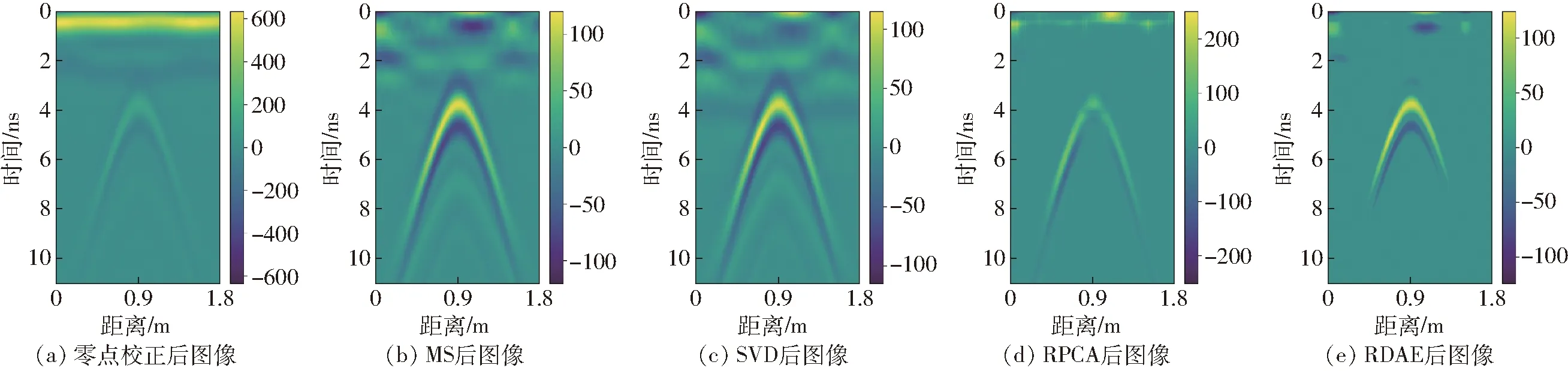
图8 不同方法对仿真数据的杂波抑制结果Fig.8 Clutter suppression results for simulated data with different methods

表2 仿真和实测数据的IF结果Tab.2 IF results of simulated and real data

实测数据通过预埋树根的方式采集，香樟树枝预埋深度为0.3 m，填埋介质为沙子。天线频率设置为400 MHz，天线移动步长0.01 m，沿着4 m长的测线进行扫描。获得的探地雷达B-scan图像包含313×409个像素点。扫描区域的原始探地雷达B-scan图像经零点校正后如图9a所示。观察到目标回波信号出现在10 ns内，因此在杂波抑制前对原始数据进行时变增益，降低其在10 ns往后的信号强度。图9b～9e分别为使用MS、SVD、RPCA和RDAE方法对图9a进行杂波抑制后的结果。由于不平整表面的影响，MS和SVD呈现相似的结果，杂波抑制后的目标图像仍包含一些杂波部分，但去除了2个最大奇异值的SVD降低了目标信号的强度，IF值低于MS。RPCA方法将目标与杂波分离良好，基于RDAE的杂波抑制方法可以更有效地从原始B-scan图像中提取目标响应，并且在4种杂波抑制方法中具有最清晰的背景、最高的IF值。

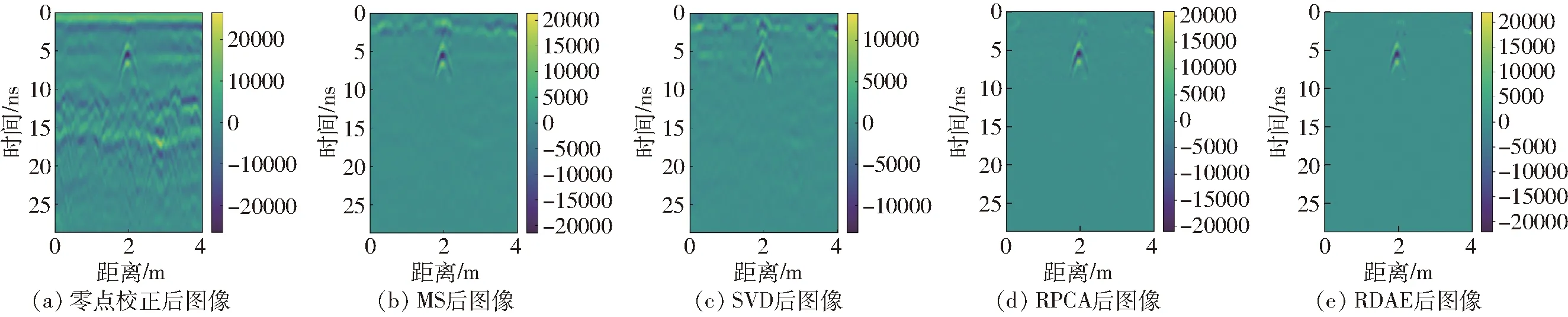
图9 不同方法对真实数据的杂波抑制结果Fig.9 Clutter suppression results for real data with different methods

2.3 相对介电常数估计

为了评估使用直接最小二乘法估计介质相对介电常数的准确性，在gprMax中模拟了12种不同的均质土壤，相对介电常数从2(干燥土壤)到13(潮湿土壤)。通过计算均方根相对误差(Root-mean-square relative error, RMSRE)来评估准确性。

按照图2所示流程，土壤相对介电常数的估计结果如图10所示，拟合真实值和估计值得到拟合曲线为y=0.965x-0.018，均方根相对误差为3.84%，相对介电常数估计有较高的准确性。

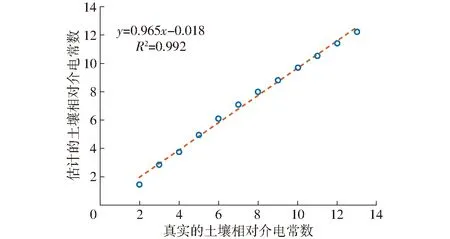
图10 用DLS估算土壤相对介电常数的结果Fig.10 Results of soil relative permittivity estimation using DLS method

2.4 根系定位

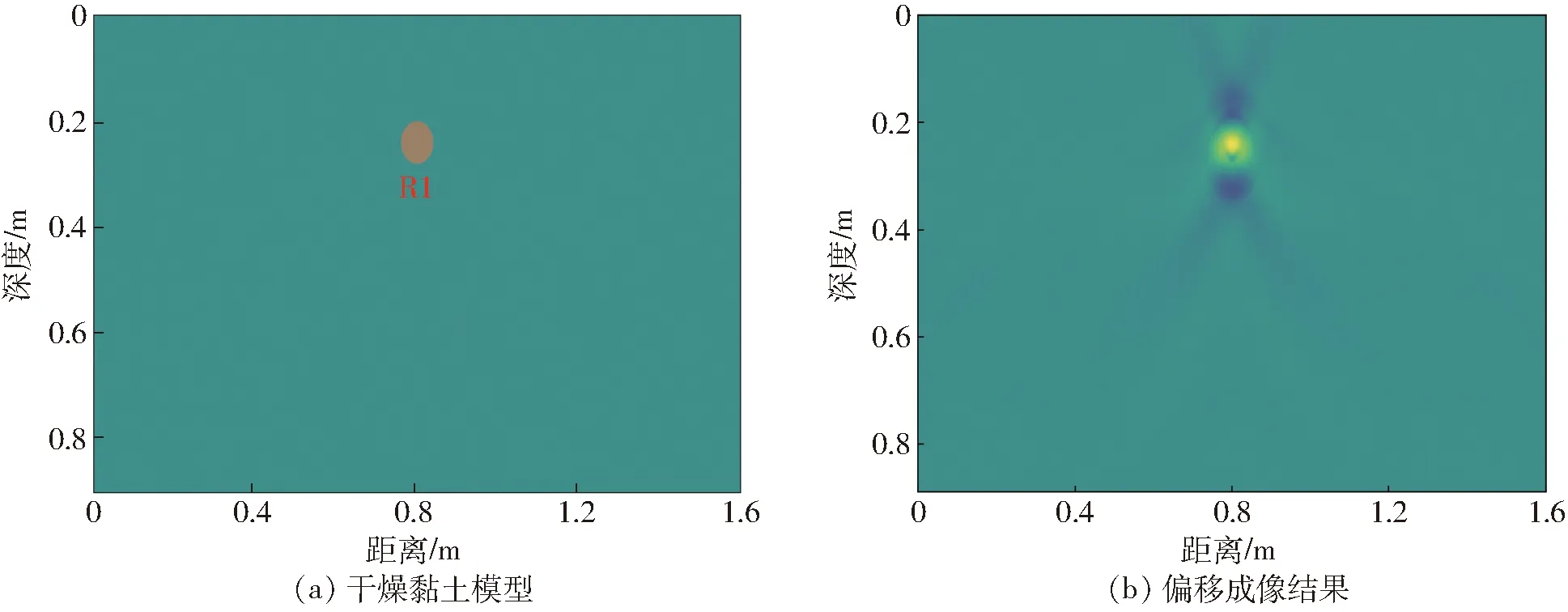
图11 均质土壤单根偏移成像结果Fig.11 Migration imaging results of single tree-root in homogeneous soil

对图7中的分层模型进行偏移成像，在使用DLS估计模型相对介电常数时，为方便计算将其视为均一介质计算模型的等效介电常数[31]，得到整个模型相对介电常数为7.29，偏移速度为0.111 m/ns，将其作为F-K偏移的输入，得到图12a所示偏移成像结果，图像中双曲线未完全消除，偏移速度小于实际速度，点状目标未能很好地聚焦。当速度增大为0.117 m/ns时，偏移成像如图12b所示，能很好地聚焦于一点。

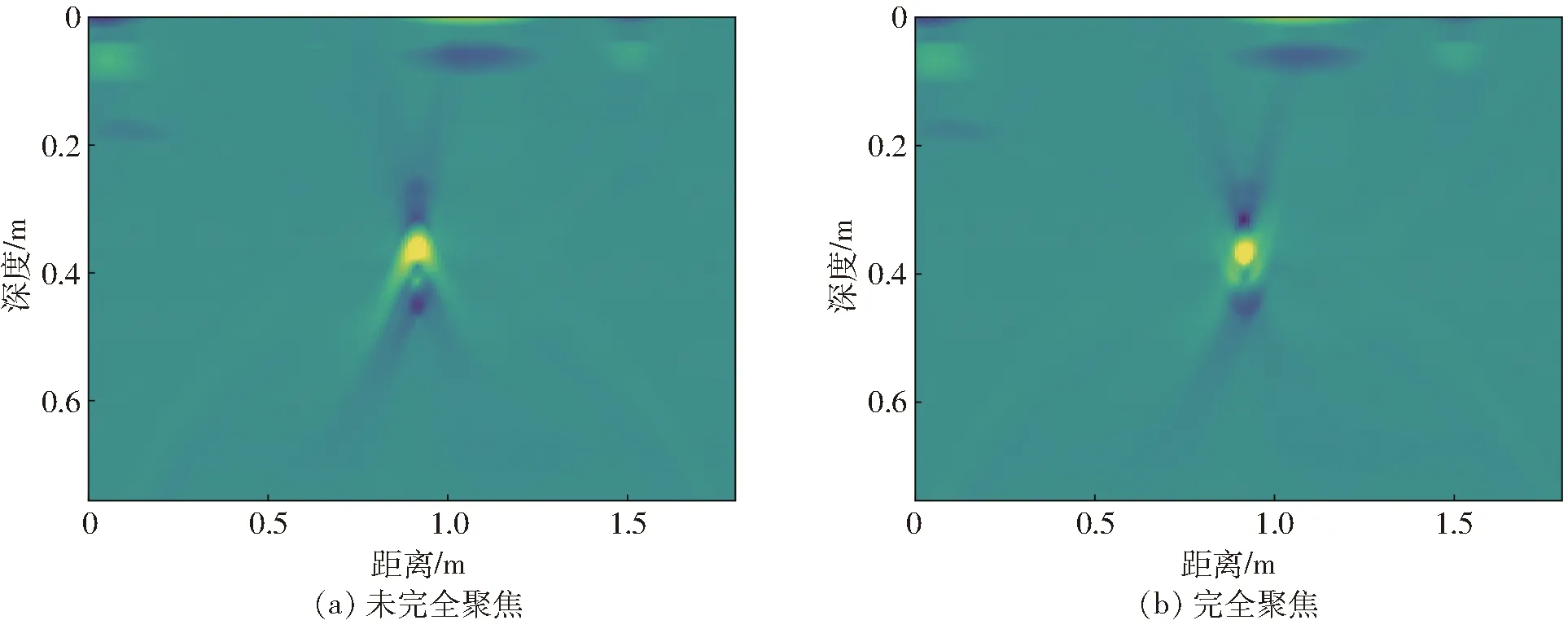
图12 分层模型单根偏移成像结果Fig.12 Migration results of single tree-root in stratified model

图13a为2.2节中实测模型的实物图，将半径0.052 m的香樟树枝R3埋在0.3 m深的沙子中，对杂波抑制后的图像(图9e)使用DLS估算出的沙子相对介电常数为12.46，偏移速度为0.085 m/ns，图13b为偏移成像结果。在相同的沙子介质中，依次放置R4、R5、R6这3个半径不同的香樟树枝于0.15、0.25、0.35 m深处，如图13c所示。图13d为杂波抑制后的偏移成像结果。

图13 实测数据偏移成像结果Fig.13 Migration results of real data

2.5 根系定位结果及分析

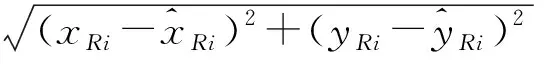
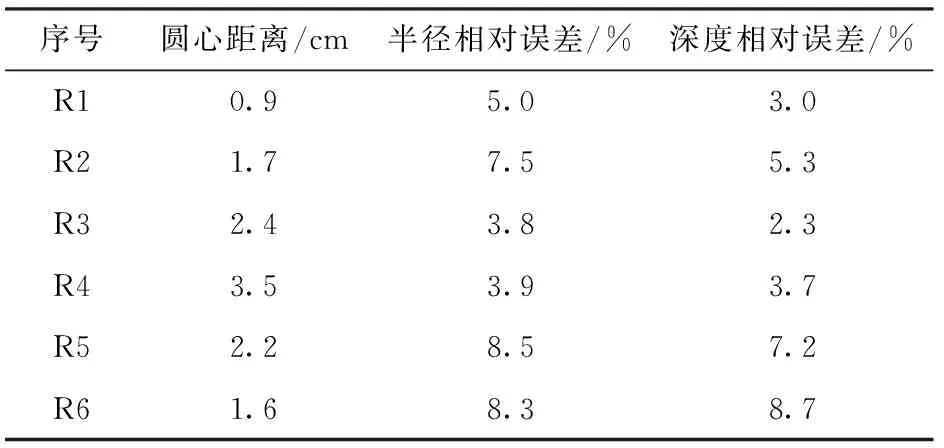
表4 偏移前后根系参数对比Tab.4 Comparison of tree-root parameters before and after migration

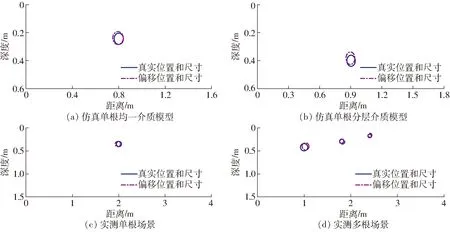
图14 偏移前后根系位置和尺寸对比Fig.14 Comparison of tree-root position and size before and after migration

表3 偏移前后根系参数对比Tab.3 Comparison of tree-root parameters before and after migration m

本文利用探地雷达检测仪在检测区域内扫描根系，收集数据，相较于根钻法和全根挖掘法等传统破坏性检测方法，检测快速，劳动成本低并且不会对周围根系造成不可逆转的破坏。为了进一步说明本文方法的优势，以文中仿真城市路面结构的B-scan图像和根R3的实测B-scan图像为样本，针对杂波抑制、双曲线拟合及偏移成像3个步骤，分别对比了与RPCA、HT和Kirchhoff偏移的计算耗时。仿真的B-scan图像尺寸为3 393×180，即由180个A-scan迹线组成，每个A-scan迹线包含3 393个采样点，实测的B-scan图像尺寸为313×409，表5为仿真数据和实测数据在根系定位3个步骤与其它方法的计算耗时对比，虽然RDAE对单个B-scan图像耗时大于RPCA，但是RDAE方法具有更高的信杂比和IF值，并且可以使用预训练的深度自动编码器降低对多个B-scan图像的杂波抑制时间。DLS和F-K偏移分别在双曲线拟合和偏移成像步骤中计算耗时低于HT和Kirchhoff偏移，总体来说，本文所提的方法在计算耗时上优于其它3种方法。

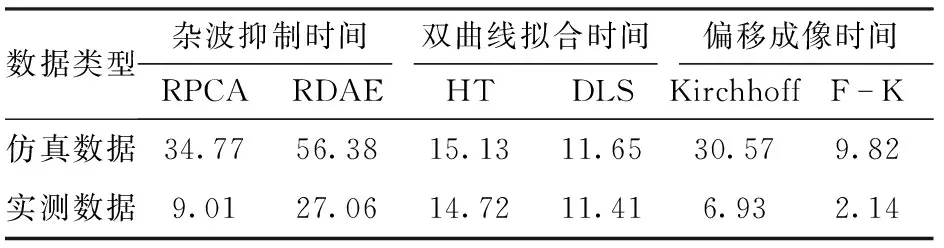
表5 计算耗时对比Tab.5 Comparison of computational time s

3 结论

(1)将探地雷达B-scan图像建模成表示杂波的低秩矩阵和表示目标回波的稀疏矩阵，杂波抑制问题转换为低秩和稀疏矩阵分解问题。实验表明，本文提出的RDAE杂波抑制方法在仿真和实测数据的杂波抑制效果均优于RPCA等传统方法，杂波抑制后的图像拥有更清晰的背景和更高的IF值。

(2)DLS拟合双曲线能更精确地估计土壤的相对介电常数，在数值模拟实验中估算的土壤相对介电常数的均方根相对误差为3.84%，为F-K偏移提供了可靠的输入。

(3)对于根系定位问题，本文提出基于RDAE杂波抑制的F-K偏移根系定位方法，在仿真和实测数据上都有较高的定位精度，偏移位置与真实位置的最大圆心距离为3.5 cm，最大半径相对误差和最大深度相对误差分别为8.5%、8.7%，能够应对复杂的分层介质模型，满足实际应用中树木根系无损检测的需求。