不同导叶开度下立式蜗壳离心泵失速特性分析

张德胜 杨雪琪 杨 港 许 彬 赵睿杰

(江苏大学国家水泵及系统工程技术研究中心， 镇江 212013)

0 引言

立式蜗壳离心泵具有流量大、扬程高、功率大的特点，是调水工程中重要的水力机械设备。为了满足不同季节、不同扬程工况下的输水要求，立式蜗壳离心泵性能指标要求较高，运行工况复杂。由于四季更替，立式蜗壳离心泵通常需在较宽流量范围内运行，而在小流量工况下叶道内会产生流动分离和各种旋涡从而堵塞流道造成失速[1-2]，并且伴随流量-扬程曲线出现正斜率[3-4]。失速现象的出现通常会使机组的水力损失增加，性能下降[5-6]，严重时通常会诱发较强的低频压力脉动，使得立式蜗壳离心泵内流态恶化、振动加剧，严重威胁机组运行的安全性和可靠性[7-9]。

国内外学者对离心泵中失速现象开展了许多研究。文献[10-11]研究了离心泵在失速工况运行时的不稳定流动现象以及失速先兆。文献[12]发现流量的改变影响了失速团的产生位置和传播方向。文献[13]探究了进口来流情况与离心泵叶轮内失速类型的联系。文献[14]利用SST-SAS湍流模型研究了叶轮内旋转失速对离心泵稳定性的影响，发现叶轮内旋涡反复的产生、发展、衰退和溃灭。随着研究的深入，探究几何参数对失速特性的影响也逐渐引起了学者们的重视[15]。文献[16-17]通过大涡模拟发现离心泵内失速的类型取决于叶轮叶片数。文献[18]研究了混流泵不同叶顶间隙下的失速特征，发现叶顶间隙的不同使得叶道内的失速团数量和失速传播规律发生改变。文献[19]研究了叶轮进口直径、叶轮出口宽度等几何因素对离心泵内流量-扬程曲线正斜率现象的影响。

由上述文献分析可见，目前对离心泵内失速现象的研究主要集中在叶轮内失速表现形式以及传播机理等方面。然而就导叶的几何参数对离心泵失速特性影响的相关研究还很有限，随着我国珠江三角洲水资源配置工程的建设，大型立式蜗壳泵站的安全稳定运行尤为重要。因此，本文通过讨论不同导叶开度对离心泵内失速特性的影响，探究导叶开度与失速现象的关联，以期为大型蜗壳泵多工况运行提供指导。

1 物理模型与数值模拟方法

1.1 物理模型及参数

本文的物理模型为立式蜗壳离心泵，其基本设计参数为设计流量Qdes=0.214 m3/s，扬程H=18 m，额定转速n=1 150 r/min，比转数ns=215，叶轮出口直径D2=360 mm，叶片数Z=7，导叶数Zd=20。该泵由进水管、离心式叶轮、活动导叶、固定导叶以及螺旋形蜗壳组合而成，如图1所示。

图1 立式蜗壳离心泵物理模型Fig.1 Physical model of vertical volute centrifugal pump1.蜗壳 2.固定导叶 3.活动导叶 4.叶轮 5.进水管

1.2 网格划分

本文采用六面体结构化网格进行划分，如图2所示。考虑流动分离和旋涡等流态，对叶轮和导叶的近壁面进行了网格加密。叶轮和导叶壁面的y+普遍小于50，如图3所示。

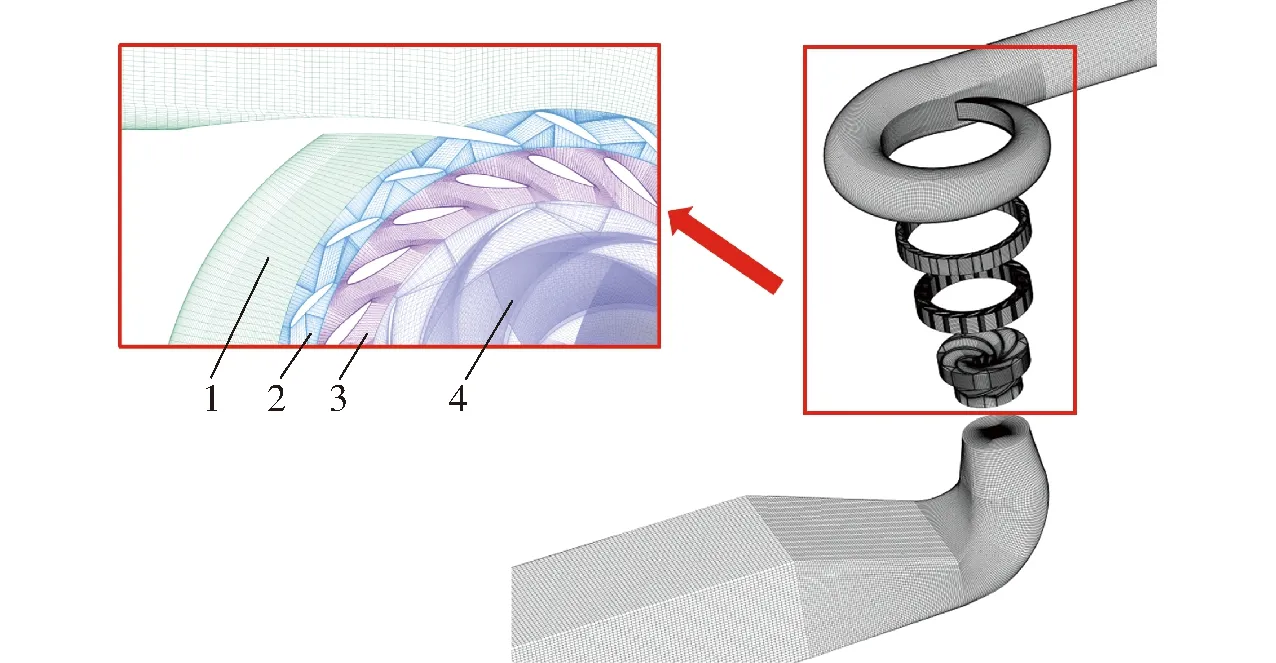
图2 立式蜗壳离心泵计算域网格Fig.2 Grid of vertical volute centrifugal pump1.蜗壳 2.固定导叶 3.活动导叶 4.叶轮

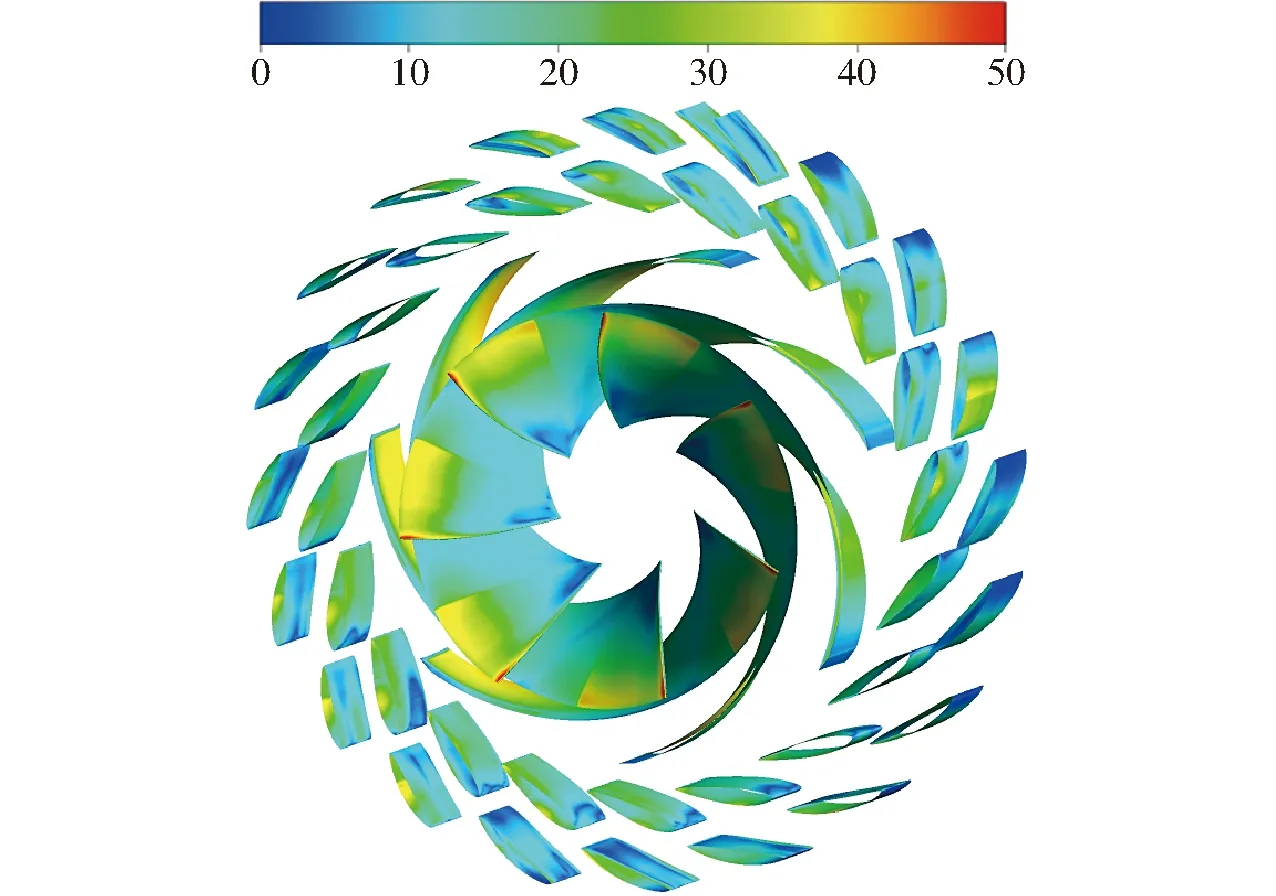
图3 叶轮和导叶的y+分布Fig.3 y+ distribution of impeller and vane diffuser

进行如图4所示的网格无关性验证，图中扬程系数CH定义为

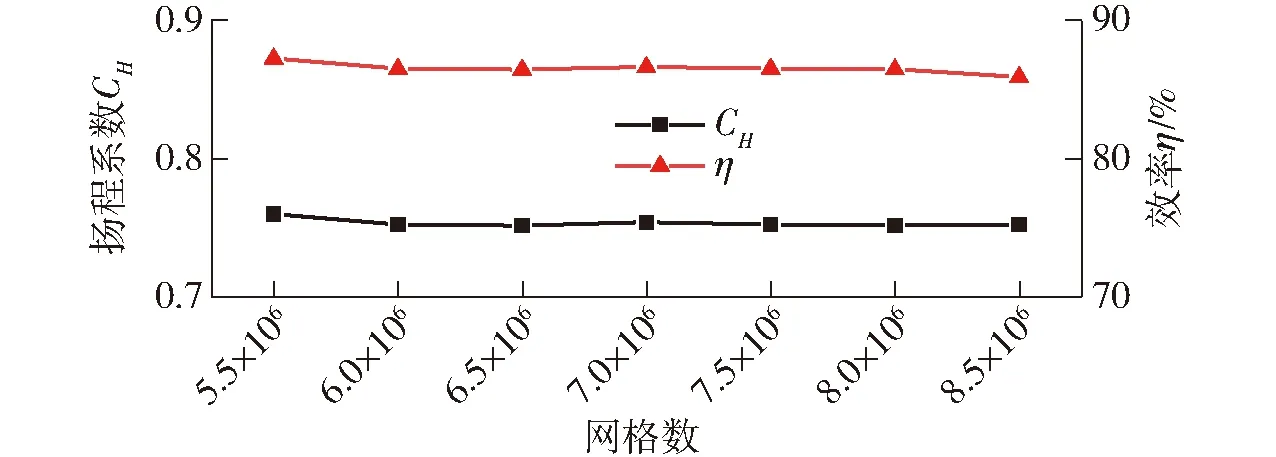
图4 网格无关性验证Fig.4 Mesh independence

(1)

其中

式中g——重力加速度，m/s2

u2——叶轮出口圆周速度，m/s

由图4可知，当网格数大于700万时，随着网格数的增加，对应的扬程和效率几乎没有差异。因此，最终确定总网格数为700万。

1.3 湍流模型及边界条件设置

在失速工况附近，泵内存在较严重的流动分离现象，湍流强度较大，且具有一定的周期性和瞬时性，故非定常数值模拟时对湍流模型的选择需要谨慎。大涡模拟(LES)模型对于捕捉流场细节有较好的效果，但计算量较大。而SST-SAS模型主要应用于分离区域[20-21]，该模型在这一区域的功能与LES模型类似[22]，但计算量相对小。综合考虑计算效果要求和计算空间限制，定常计算时采用SST湍流模型，非定常计算选用SST-SAS湍流模型。SAS模型将von Karman长度尺度LνK引入到SST湍流模型的尺度确定方程中[23]，其中LνK定义为

(2)

其中

式中U′、U″——速度一阶、二阶导数

Ui、Uj——速度分量

xi、xj——x、y方向分量

Sij——应变率张量

κ——von Karman常数，取0.41

SST-SAS湍流模型在SST模型的ω方程产生项的基础上附加了QSAS项[24]，QSAS描述为

QSAS=max(A-B,0)

(3)

其中

式中k——湍动能，m2/s2

ω——比耗散率，m2/s3

ζ2、cμ、C、σΦ——常数，分别为3.51、0.09、2.0、2/3

数值模拟前处理时设置进水管进口边界为一个大气压，蜗壳出口边界与质量流量Qm有关。壁面函数为无滑移壁面边界条件。收敛精度设置为10-5。在非定常计算时，时间步长设置为3°，即4.35×10-4s，每个时间步长中最大迭代次数为15次。计算时长为1.04 s，即20个转动周期。压力-速度耦合运用SIMPLEC算法。数值模拟使用二阶迎风格式求解。

1.4 试验验证

为保证数值模拟结果的可靠性，通过模型机试验展开验证。在水利部天津中水北方勘测设计研究院水力模型试验台上开展性能试验，试验装置系统如图5所示。试验台以及主要转动部件叶轮的实物图如图6所示。

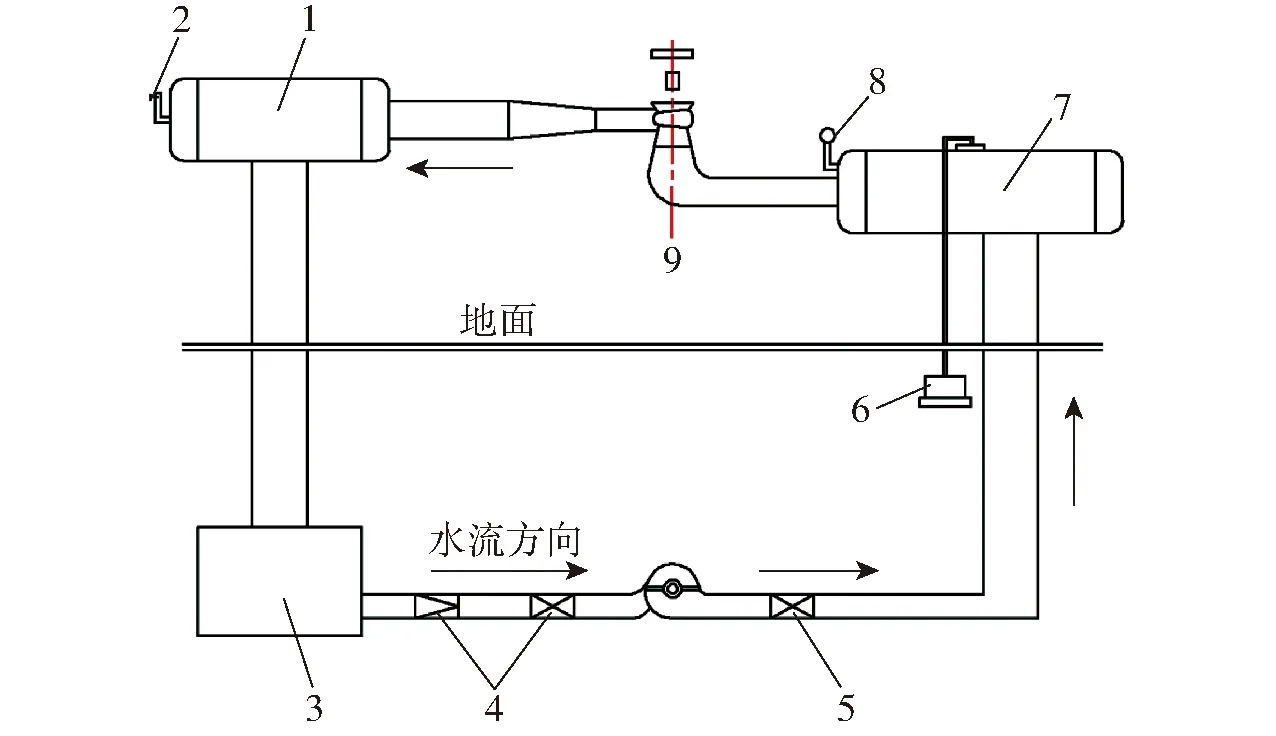
图5 试验装置系统图Fig.5 System diagram of test devices1.高压罐 2.空气阀 3.蓄水池 4、5.阀门 6.真空泵 7.低压罐 8.压力表 9.试验泵

图6 试验设备实物图Fig.6 Physical diagram of test equipment1.电机 2.试验段 3.叶轮

当立式蜗壳离心泵在小流量工况区运行时流量-扬程曲线通常会出现正斜率，效率也会随之突降，严重影响该泵的稳定高效运行。为了预测该立式蜗壳离心泵的失速区，本文选取了24个工况点进行了数值模拟，并在流量-扬程曲线出现正斜率的区域增加了模拟工况点，以获得准确的失速工况位置。同时，为检验瞬态数值模拟的可靠性，对多个工况下的瞬态模拟结果取时均值后绘制性能曲线。最后，将模拟曲线与试验曲线进行了对比，如图7所示。在所有测量工况范围内，扬程和效率的模拟值和试验值偏差均在5%以内，说明数值模拟能够较为准确地预测该立式蜗壳离心泵的能量特性。且瞬态的数值模拟结果与试验结果更为接近。图中流量系数CQ定义为

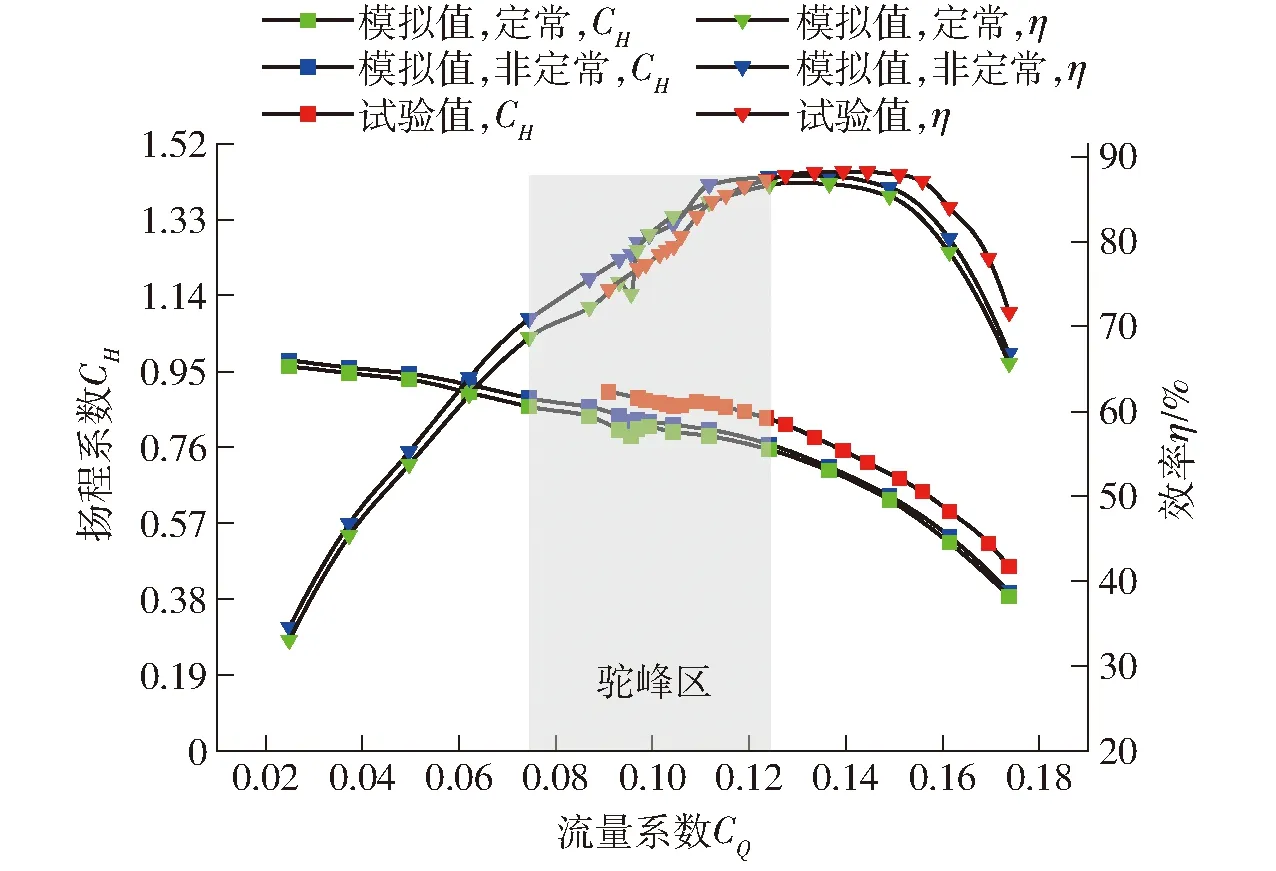
图7 外特性模拟曲线与试验曲线Fig.7 Performance curves of simulation and experiment

(4)

式中Q——泵的流量,m3/s

b2——叶轮出口宽度，取0.070 3 m

2 结果与讨论

2.1 不同导叶开度下泵内流动特性

2.1.1水力性能对比

3种开度下立式蜗壳离心泵的性能曲线如图8所示。其中，小开度时活动导叶开度为19°，最优开度时为25°，大开度时为31°。

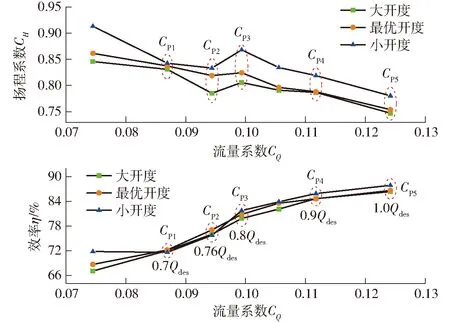
图8 不同开度下立式蜗壳离心泵的性能曲线Fig.8 Performance curves of vertical volute centrifugal pump at different openings

由图8可知，3种导叶开度下流量-扬程曲线在CP2～CP3流量范围内均出现正斜率，即存在驼峰区。小开度时正斜率区域的对应斜率最大，最优开度时最小。结合流量-效率曲线可知，在临界失速工况(CP3工况)时小开度对应的效率最大，而在深度失速工况(CP2工况)时小开度对应的效率最小。故小开度下当流量从临界失速工况下降到深度失速工况时，效率的骤降最为明显。由此可知，小开度下当立式蜗壳离心泵发生失速后，泵内流态发生较大变化，造成扬程的剧烈减小以及效率的陡降。同时，随着导叶开度的增大，立式蜗壳离心泵的扬程整体上减小。

2.1.2导叶内涡量场分析

由于活动导叶开度的改变，直接影响了导叶流域的流态，故本文首先探讨了导叶内的流动差异性。选取深度失速工况时流道内涡量分布进行研究，如图9所示。

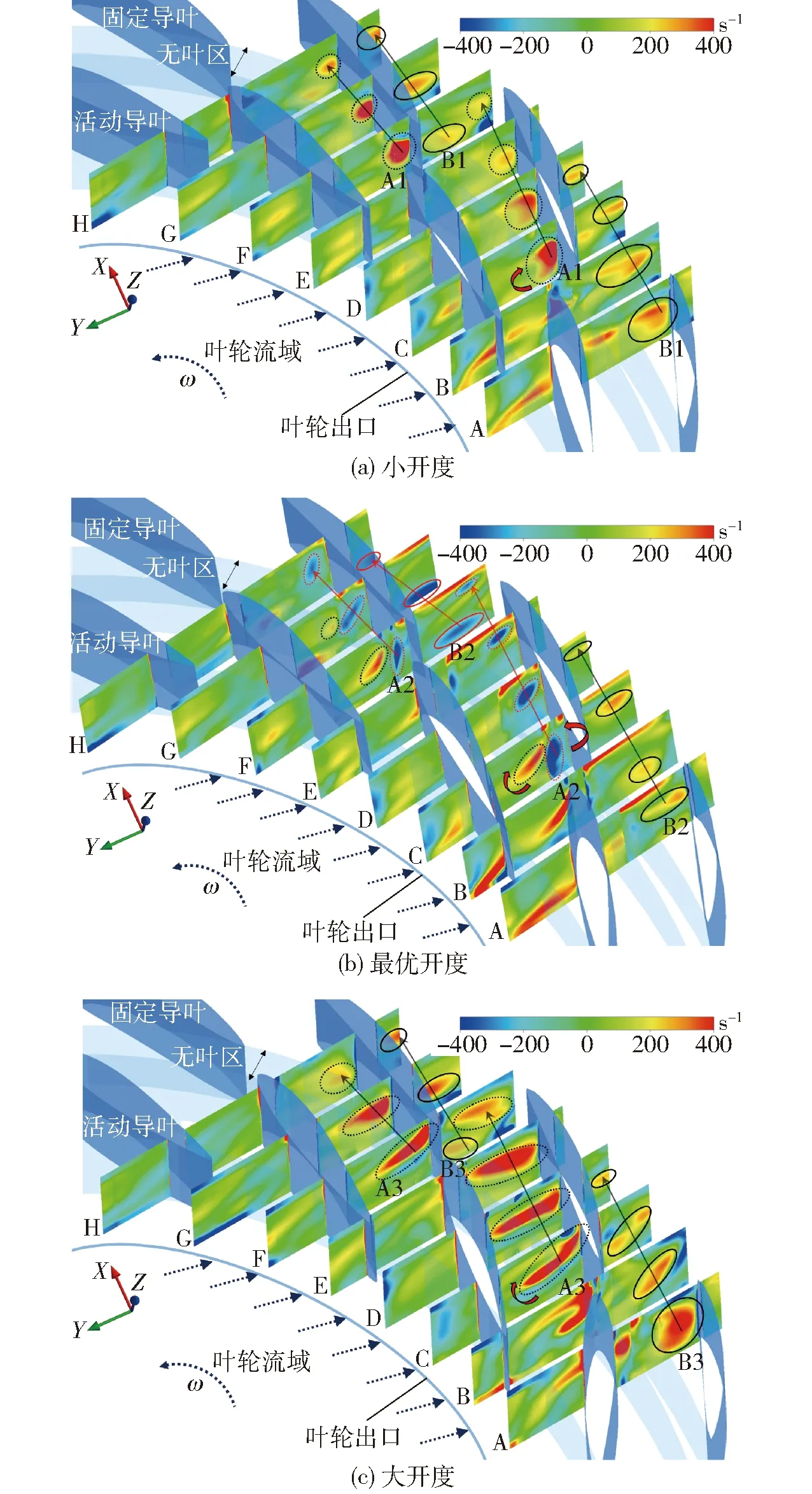
图9 不同开度下导叶内的涡量分布(CP2工况)Fig.9 Vorticity distribution in vane diffuser at different openings (condition CP2)

由图9可知，在3种导叶开度下，活动导叶与固定导叶之间的无叶区内均出现了高涡量区域。且旋涡沿固定导叶工作面前缘向后缘延伸，旋涡强度逐渐减小，如图中虚线框位置所示(见标识A)。小导叶开度和大导叶开度下，该位置存在的旋涡均是沿顺时针方向旋转，且大开度时旋涡强度大，覆盖面积广。最优开度时旋涡强度相对较小，但在活动和固定导叶间的无叶区出现两种旋向相反的旋涡。

同时固定导叶工作面的旋涡，引起了相邻固定导叶背面产生旋涡，如图中实线框位置所示(见标识B)。该旋涡从固定导叶工作面尾缘向相邻固定导叶背面扩散，旋涡强度随之减小。并且该旋涡在大开度条件时强度最大，最优开度时最小。

综上所述，3种不同开度时活动和固定导叶之间的无叶区内都存在大尺度旋涡。且旋涡不断向下游扩散，造成固定导叶内流态的恶化。同时，导叶流域在大开度条件时旋涡强度最大，最优开度时相对最小。

2.1.3叶轮内熵产率分布

活动导叶开度的变化，不仅改变了导叶内的流动特性，也对相邻过流部件叶轮内的流动不均匀性造成了影响。本节借助熵产理论建立立式蜗壳离心泵内过流部件的能量损失与熵产变化之间的联系，从而获得过流部件内损失分布规律。首先，假设运输介质水是不可压缩的，且泵内的能量变化是不可逆的。其次，考虑水在流动过程中水温变化较小，故忽略由于温度上升而引起的熵增，认为过流部件内的熵产是由湍流流动造成的。该熵产主要包括两个部分，其定义为

(5)

其中

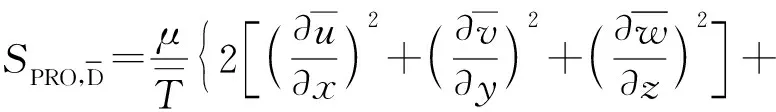
式中SPRO——湍流流动的耗散导致的总熵产率，kW/(m3·K)

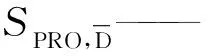
SPRO,D′——湍流脉动速度导致的熵产率，kW/(m3·K)

μ——流体动力粘度，Pa·s

u、v、w——速度在x、y、z坐标方向上的投影，m/s

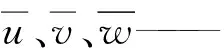
u′、v′、w′——瞬态速度分量u、v、w时均化时的脉动量，m/s

然而，由于CFD计算中采用RANS方法，无法得到湍流脉动速度，故湍流脉动速度导致的熵产率SPRO,D′则难以直接根据式(5)获得。为此文献[25]提出一种近似计算方法，描述为

(6)

式中ρ——流体密度，kg/m3

ε——湍流耗散率，m2/s3

若假设流体在立式蜗壳离心泵中流动时温度恒定，则将总熵产率定义为

(7)

根据上述熵产理论，获得深度失速工况时不同导叶开度下叶轮叶片靠近前盖板截面(Span值0.1)、叶轮叶片中截面(Span值0.5)以及叶轮叶片靠近后盖板截面(Span值0.9)的熵产率分布情况，如图10所示。

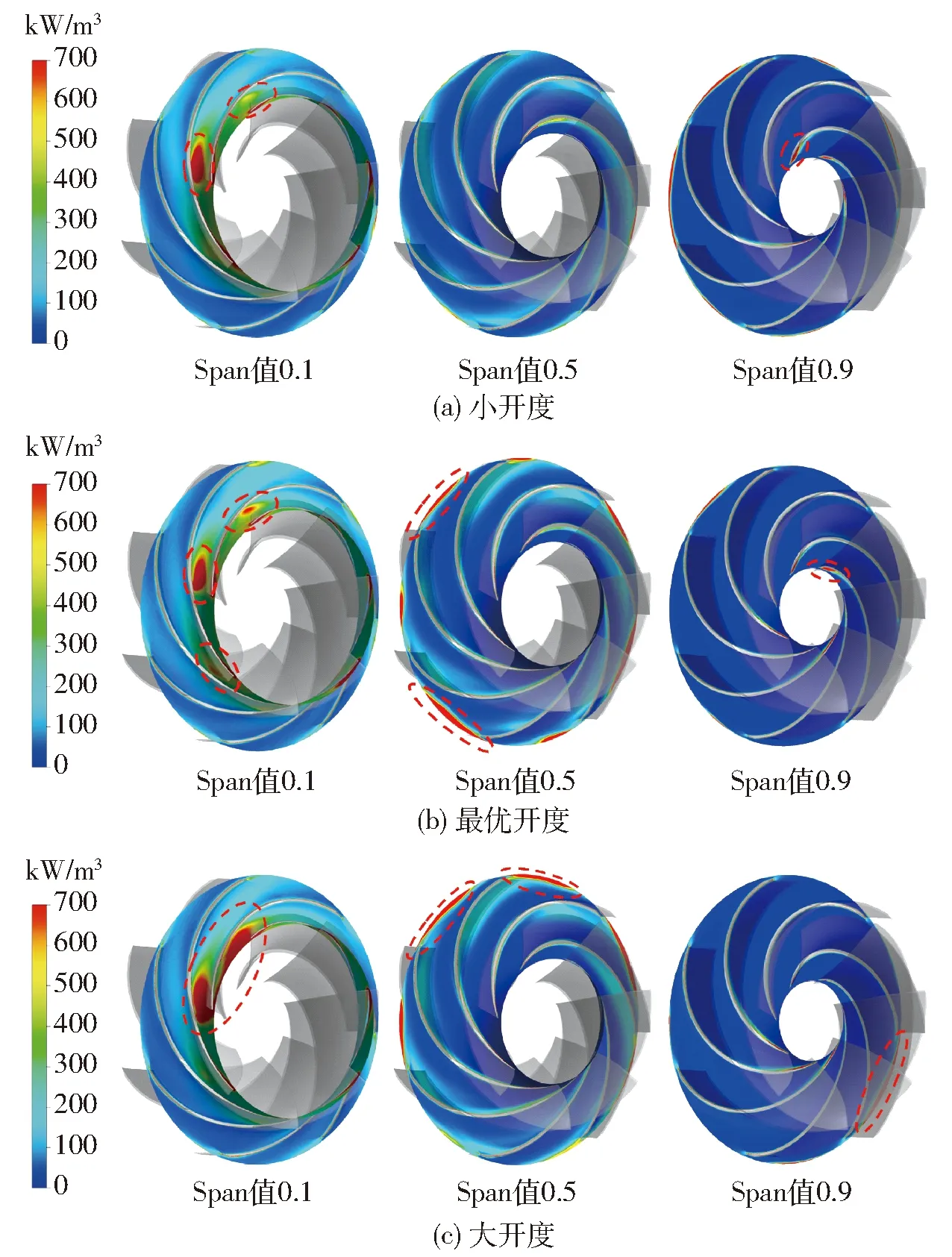
图10 不同开度下叶轮内的熵产率分布(CP2工况)Fig.10 Entropy production rate distribution in impeller at different openings (condition CP2)

由图10可知，随着活动导叶开度的增大，Span值0.1截面上的高熵产率区域不断扩大，且集中于叶轮进口附近。同时在最优开度以及大开度下，可以在Span值0.5截面上观察到较高的熵产率分布在叶轮流道靠近出口位置，某些流道的出口处十分明显。而Span值0.9位置仅在叶轮叶片前缘附近有较小的高熵产率区域。

依据熵产理论可知，过流部件内的熵产是由湍流流动造成的。而不稳定流动结构会诱导湍流脉动的产生，从而引起较大的水力损失。所以高熵产率区域对应的流动不均匀性严重，由此造成的水力损失较大。为进一步探究高熵产率区域的流态，结合叶轮内对应流线分布情况进行分析，如图11所示。

通过图10和图11可知，不同导叶开度下叶轮内高熵产率特征出现位置对应流场存在流动分离、旋涡等不稳定流动结构。同时流场中速度梯度较大位置处的熵产率也较高。由此可知，Span值0.1截面的流态随着导叶开度增大而恶化，旋涡覆盖面积扩大。Span值0.5截面处，当导叶为最优开度以及大开度时，叶轮出口附近出现较大的速度梯度。而Span值0.9截面处，可以在叶轮叶片前缘吸力面位置观察到较小的旋涡，在叶轮出口附近也存在局部较大速度梯度。

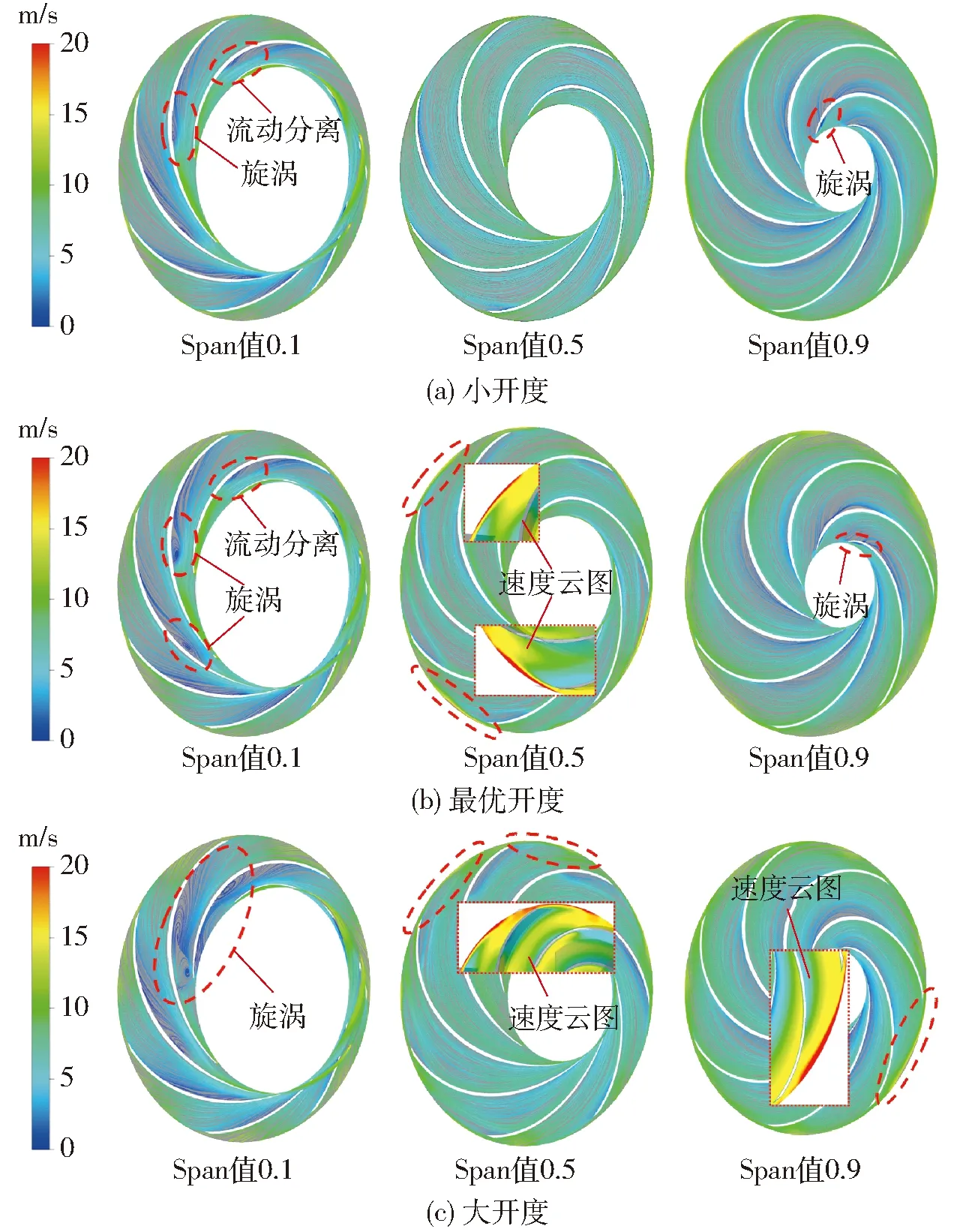
图11 不同开度下叶轮内的流线分布(CP2工况)Fig.11 Streamline distributions in impeller at different openings (condition CP2)

2.2 不同导叶开度下压力脉动分析

当立式蜗壳离心泵在失速工况运行时，导叶内流动分离和旋涡的存在通常会诱发不稳定的压力波动。为更好地研究压力脉动变化情况，在导叶流道中截面内设置了如图12所示监测点。图12中在活动导叶中间流道r=214 mm处沿圆周方向均布了20个监测点。

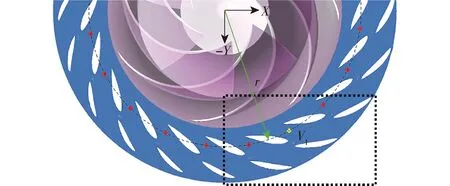
图12 截面处监测点的布置Fig.12 Distribution of monitoring points on cross-section

图13为通过快速傅里叶变换(FFT)得到的不同导叶开度下监测点V1在深度失速工况时的压力脉动频域图，其中压力系数Cp定义为

图13 监测点V1的压力脉动频域图(CP2工况)Fig.13 Frequency spectra of pressure fluctuation at monitoring point V1 (condition CP2)

(8)

式中p——瞬态压力，Pa

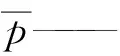
由图13可知，随着导叶开度的增大低频信号愈加复杂且对应振幅不断增加。小开度时压力脉动的主频f=7fn=134 Hz(fn为轴频)，即为叶片通过频率。同时也可以观察到叶片通过频率的高次谐波。由此可知，小开度时深度失速工况下的压力脉动主要受到叶轮与导叶间的动静干涉作用影响。而最优开度时主频为0.9fn，大开度时在0.7fn～1.2fn范围内频率对应振幅均较大，呈现宽频特性。这些低频压力信号的出现可能是由导叶内的流动分离和旋涡造成的。为进一步阐明低频信号出现原因，选取最优开度下不同时刻导叶中截面上的瞬态流动结构进行研究，如图14所示。其中T0为某一时刻，T为叶轮一个旋转周期。

由图14可知，在T0时刻，可以在固定导叶吸力面前缘附近观察到一个大尺度旋涡。然而在T0+0.45T时刻，该位置的旋涡消失。T0+0.9T时刻该位置附近又出现了旋涡。在T0+1.35T时刻，该位置的流态又恢复顺畅。当T0+1.8T时刻时，又出现了旋涡，且旋涡尺度较大。即每经过0.9T时间，该旋涡就会出现一次。由此可知，最优开度时深度失速工况下主频为0.9fn与导叶内存在的周期性大尺度旋涡密切相关。

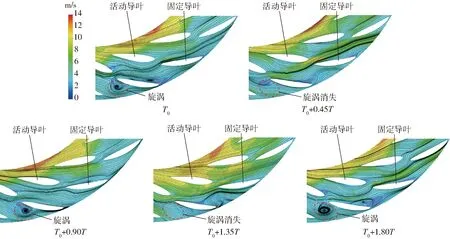
图14 导叶内不同时刻的速度分布(CP2工况)Fig.14 Velocity distribution of vane diffuser with different time (condition CP2)

3 结论

(1)导叶开度对立式蜗壳离心泵流量-扬程水力性能曲线影响较大。随着导叶开度的增大，扬程整体上减小。不同导叶开度下失速特征工况点不变，但小开度时失速区流量-扬程曲线对应斜率最大，最优开度时最小。

(2)固定和活动导叶间无叶区内的旋涡在3种活动导叶开度下均较为严重，且大开度时旋涡强度最大，最优开度时最小。同时固定导叶工作面的旋涡扩散至相邻固定导叶背面。

(3)在深度失速工况下，不同导叶开度下叶轮内的流体熵产率分布规律呈现明显不同的特征。叶轮叶片靠近前盖板截面上的高熵产区域随导叶开度的增大而扩大。叶轮叶片中截面上，在最优开度和大开度时叶轮流道靠近出口位置出现较大熵产。叶轮叶片靠近后盖板截面上的熵产整体较小。通过对比分析发现流动分离、旋涡等不稳定流动结构会诱导湍流脉动的产生，造成局部高熵产率。

(4)小开度时深度失速工况下压力脉动的主频为叶片通过频率，而最优开度和大开度时主频为低频信号。通过对导叶内瞬态流场的分析可知，低频信号占据主导地位与导叶内出现的大尺度旋涡密切相关。