基于石墨烯和二氧化钒的太赫兹宽带可调谐超材料吸收器
刘苏雅拉图,王宗利,庞慧中,田虎强,王 鑫,王俊林
内蒙古大学电子信息工程学院,内蒙古 呼和浩特 010021
引 言
超材料(metamaterials, MMs)是一种由周期性排列的亚波长单元组成的人工复合材料,具有自然材料所不具备的超常电磁性质,例如负折射率、电磁诱导透明、逆多普勒效应等[1]。 近年来,超材料由于这些特殊的电磁性质逐渐成为了研究热点,在生物成像、电磁隐身、完美透镜和无线通信等领域具有广阔的应用前景[2]。 2008年,Landy等提出基于电磁超材料的吸收器,实现了对特定电磁波的完美吸收[3]。 此后,研究人员设计出了不同吸波频段的超材料吸收器,包括微波段、太赫兹波段、红外波段以及可见光波段[4-7]。 但是,目前大部分的超材料吸收器的结构一旦制备成型,它的吸收性能便不再改变,只能实现对固定频段的电磁波的吸收,难以满足复杂多变的电磁环境的要求,因此对于主动可调谐超材料吸收器的开发需求日益迫切。 目前,可通过改变温度、外加光泵或施加电场等方式改变材料的电导率和介电常数来实现工作频率、吸收率的主动调节。
石墨烯(Graphene)和二氧化钒(VO2)因具有特殊的性质而被人们广泛关注,石墨烯的电导率与自身费米能级有关,因此可以通过外加偏置电压或化学掺杂等方式改变石墨烯的费米能级,从而实现对基于石墨烯的超材料吸收器的动态调谐。 2016年,Yao等设计出了一种双频段超材料完美吸收器。 该吸收器由椭圆形纳米圆盘石墨烯结构和由SiO2介质隔开的金属层组成,可以通过外加电压方式控制石墨烯的费米能级实现共振频率的调节[8]。 二氧化钒是一种热控相变材料,它的电导率在相变过程中会发生巨大突变。 当低于临界温度(68 ℃) 时二氧化钒表现为绝缘体,而高于临界温度时表现出金属特性。 因此,可利用这一特性对二氧化钒进行加热,对入射电磁波的吸收进行调控。 2019年,Song等提出了基于二氧化钒的太赫兹宽频超材料吸收器。 通过调节温度来改变二氧化钒电导率,当电导率从10 S·m-1增加到2 000 S·m-1时,吸收率可从30%连续调整到近100%[9]。 2020年,Li等提出了一种极化不敏感的双可调谐宽带超材料吸收器,通过调节石墨烯的费米能级完美吸收峰发生了1.18 THz的蓝移。 通过外部刺激改变二氧化钒的电导率,相应吸收率可以连续地从28%到99%之间调节[10]。
为了获得吸收率更高、吸收带宽更宽、工作频率与吸收振幅双重调控的超材料吸收器,本文提出了一种基于石墨烯和二氧化钒的太赫兹宽带可调谐超材料吸收器,该吸收器由工字型二氧化钒谐振层、连续石墨烯层、Topas介质层以及底层金属板构成。 当二氧化钒材料处于全金属状态且石墨烯的费米能级设为0.1 eV时,在1.70~4.50 THz频带内获得了吸收率高于90 %以上的吸收性能。 当二氧化钒材料处于全金属状态且石墨烯的费米能级在0.1~0.3 eV之间变化时,宽频吸收光谱会发生明显的蓝移。 当石墨烯的费米能级保持为0.1 eV时,通过温度控制改变二氧化钒的电导率从100 S·m-1变化到200 000 S·m-1时,宽频超材料在全反射和全吸收之间自由切换。 此外,利用有限元仿真软件CST对该吸收器顶层与底层的表面电流分布进行仿真与分析,阐述了其对入射电磁波的吸收机理。 本文设计的可调谐宽带吸收器结构简单、功能多样化,在电磁隐身、移动通信、医疗传感等领域具有广阔的应用前景。
1 实验部分
提出的基于石墨烯和二氧化钒的太赫兹宽带可调谐超材料吸收器的结构示意图如图1所示,它包含四层结构,自上至下分别为工字型二氧化钒谐振结构阵列、连续单层石墨烯、Topas介质层以及底层的连续金属板。 其中工字型二氧化钒谐振器与X轴方向呈45°夹角排列在石墨烯表面,其厚度为T1=2 μm;单层石墨烯的厚度为T2=1 nm;Topas介质相对介电常数εr=2.35[11],厚度为T3=14.5 μm;底层金属板采用电导率为σ=4.56×107S·m-1的有损耗材料金,厚度为T4=0.3 μm。 其他优化的具体结构参数如下:L1=23 μm,L2=13 μm,W=1 μm,结构单元周期为P=30 μm。
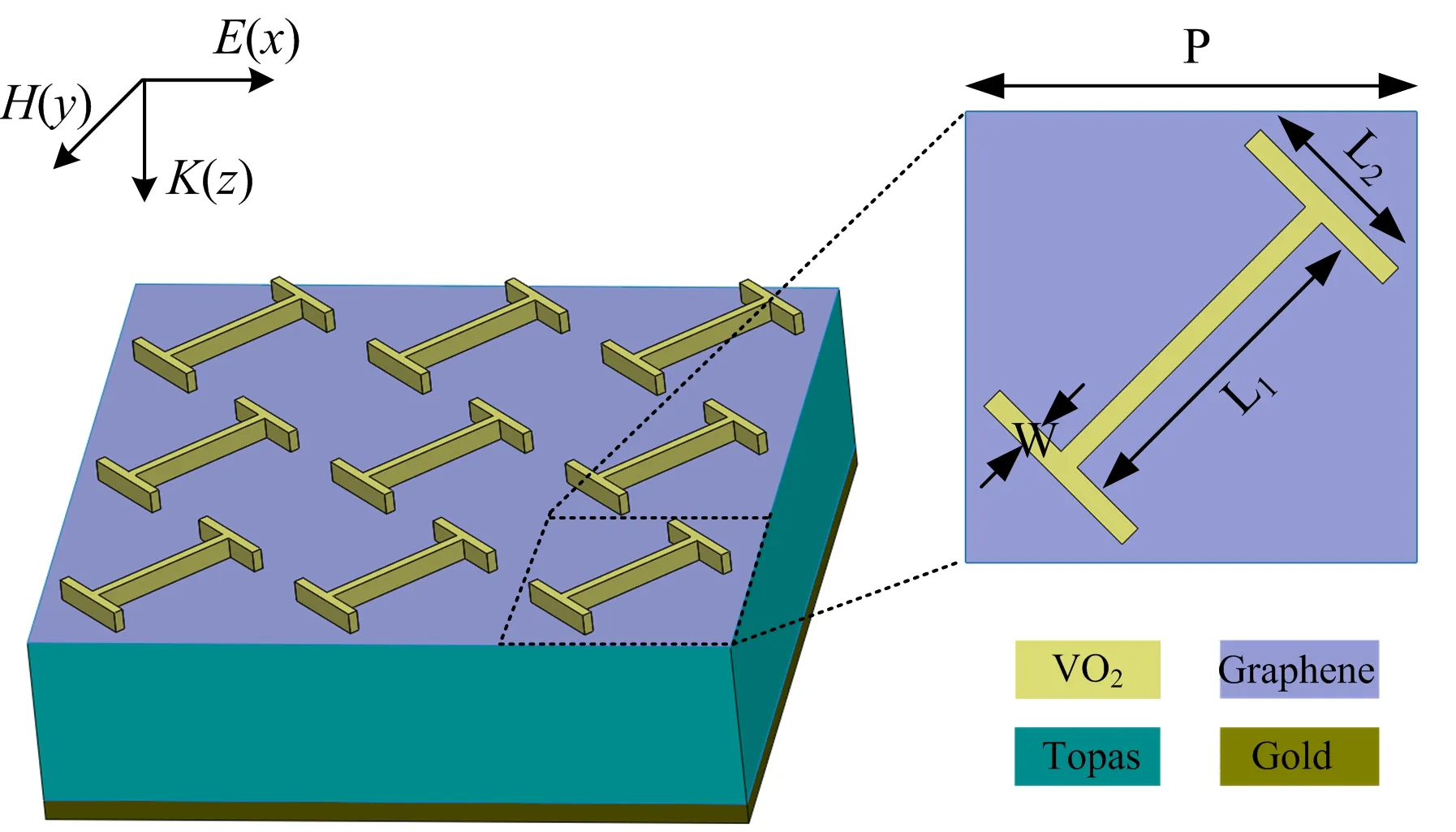
图1 基于石墨烯和二氧化钒的太赫兹宽带可调谐超材料吸收器的结构示意图
二氧化钒在68 ℃ 左右的温度下能够发生从绝缘体到金属相的可逆相变。 当二氧化钒处于绝缘相时可以看作介电常数为εr=9的无损介质,对太赫兹波段和红外波段的电磁波具有高度穿透性。 当二氧化钒处于金属相时,对应的介电常数ε(ω)可以由Drude模型描述[12],即
(1)
式(1)中,ε∞为二氧化钒的高频极限介电常数且ε∞=12;γ=5.75×1013rad·s-1为碰撞频率;σ为二氧化钒材料的电导率;ω为太赫兹波的角频率;ωp为等离子体频率,可近似表示为
(2)
式(2)中,σ0=3×103Ω-1·cm-1,ωp(σ0)=1.4×1015rad·s-1。
石墨烯是由单层碳原子排列构成的材料,在仿真过程中,石墨烯的表面电导率可以由Kubo模型来描述,石墨烯表面电导率由带内电导率和带间电导率共同影响,其计算公式为[13]
σ(ω)=σintra(ω)+σinter(ω)
(3)
(4)
(5)
式中:ω是太赫兹波角频率,e是电子的电荷量,KB是玻尔兹曼常数,T=300 K为温度,ћ=h/2π是约化普朗克常数,τ是弛豫时间,Ef是费米能级。 在太赫兹频段内,当满足ћω≪2Ef时,带间电导率可以忽略不计,石墨烯的表面电导率取决于带内电导率。 因此,石墨烯的表面电导率简化为Drude模型来描述[14]。
(6)
由式(6)可以看出,石墨烯的表面电导率除了与入射电磁波的角频率以及弛豫时间相关以外,还与其费米能级有关。 因此,我们通过给石墨烯施加偏置电压来改变石墨烯的费米能级,进而调节其表面电导率。 石墨烯的费米能级Ef与施加偏置电压Vbias之间关系为
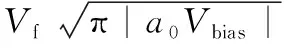
(7)
式(7)中,Vf=1×106m·s-1为费米速度,a0=9×1016m-2·V-1为电容常数。
采用电磁仿真软件CST的频域求解器对超材料吸收器的结构进行仿真。 在仿真过程中,太赫兹波沿z轴正方向垂直入射到结构表面,电场E沿着x轴方向,磁场H沿着y轴方向,xoy平面设置为周期性边界条件(unit cell),z轴方向设置为开放性边界条件(open)。 另外,超材料吸收器的吸收率由公式A(ω)=1-|S11|2-|S21|2计算得出,其中S11和S21分别表示结构的反射系数和透射系数。
2 结果与讨论
当石墨烯的费米能级设为0.1 eV且二氧化钒材料的电导率为200 000 S·m-1(即金属状态)时,顶层工字型谐振器与X轴呈45°夹角和与X轴垂直时对应的吸收光谱分别如图2(a)和(b)所示。 可以看到,当顶层工字型谐振器与X轴呈45°摆放时,在1.70~4.50 THz的宽频吸收带内吸收率超过了90%,且在1.87,3.04和4.16 THz三个频率点处吸收率分别达到了99.10%,99.95%和99.65%的完美吸收。 当顶层工字型谐振器与X轴垂直摆放时,在相同频段内最高吸收率仅有50%。 为了进一步研究超材料结构实现电磁波吸收的内在机理,本文引入了阻抗匹配理论。 吸收器的相对阻抗Z可以由仿真结果中的S参数导出来,其计算公式为[15]
(8)
图2(a)和(b)两种情况下,超材料吸收器相对阻抗的实部和虚部分别如图2(c)和(d)所示。 由图可以看到,当顶层工字型谐振器与X轴呈45°夹角,超材料吸收器的相对阻抗Z的实部接近于1,而虚部接近于0,说明该吸收器的阻抗与自由空间的阻抗相匹配,此时吸收器结构对入射电磁波的反射几乎为零,入射电磁波的大部分能量被超材料结构所吸收,实现了近乎完美的吸收。 而当工字型谐振器与X轴垂直时,超材料吸收器的阻抗与自由空间阻抗不匹配,从而降低了吸收率。

图2 顶层工字型谐振器与X轴呈45°夹角(a)吸收器的吸收光谱,(c)吸收器相对阻抗的实部和虚部;顶层工字型谐振器与X轴垂直(b)吸收器的吸收光谱,(d)吸收器相对阻抗的实部和虚部
为了进一步分析所设计的太赫兹宽带吸收器的吸收机理,在石墨烯的费米能级为0.1 eV且二氧化钒材料的电导率为200 000 S·m-1时,分别对峰值频率f1=1.87 THz,f2=3.04 THz,f3=4.16 THz处超材料吸收器顶层和底层的表面电流分布进行了仿真分析,如图3所示。 当谐振频率为f1=1.87 THz时,顶层工字型谐振单元表面的电流集中分布于工字型二氧化钒阵列的中间条带上,电流方向由上至下产生了电偶极共振,底层金属板的电流方向与顶层工字型表面相反并构成回路,激发形成了磁偶极共振。f2=3.04 THz处的顶层工字型谐振单元表面的电流主要分布在工字型上下横梁的两端,吸收机理与f1=1.87 THz处的吸收机理相同,都是在电、磁偶极共同作用下,实现了对入射波的强烈吸收。 当谐振频率移至f3=4.16 THz处,顶层工字型谐振单元表面的电流集中分布于二氧化钒谐振器的中间条带上且方向与底层金属板的电流方向一致,这是由于金属相二氧化钒材料与Topas介质层之间激发了表面等离子体共振,增强了吸收器的吸收性能。
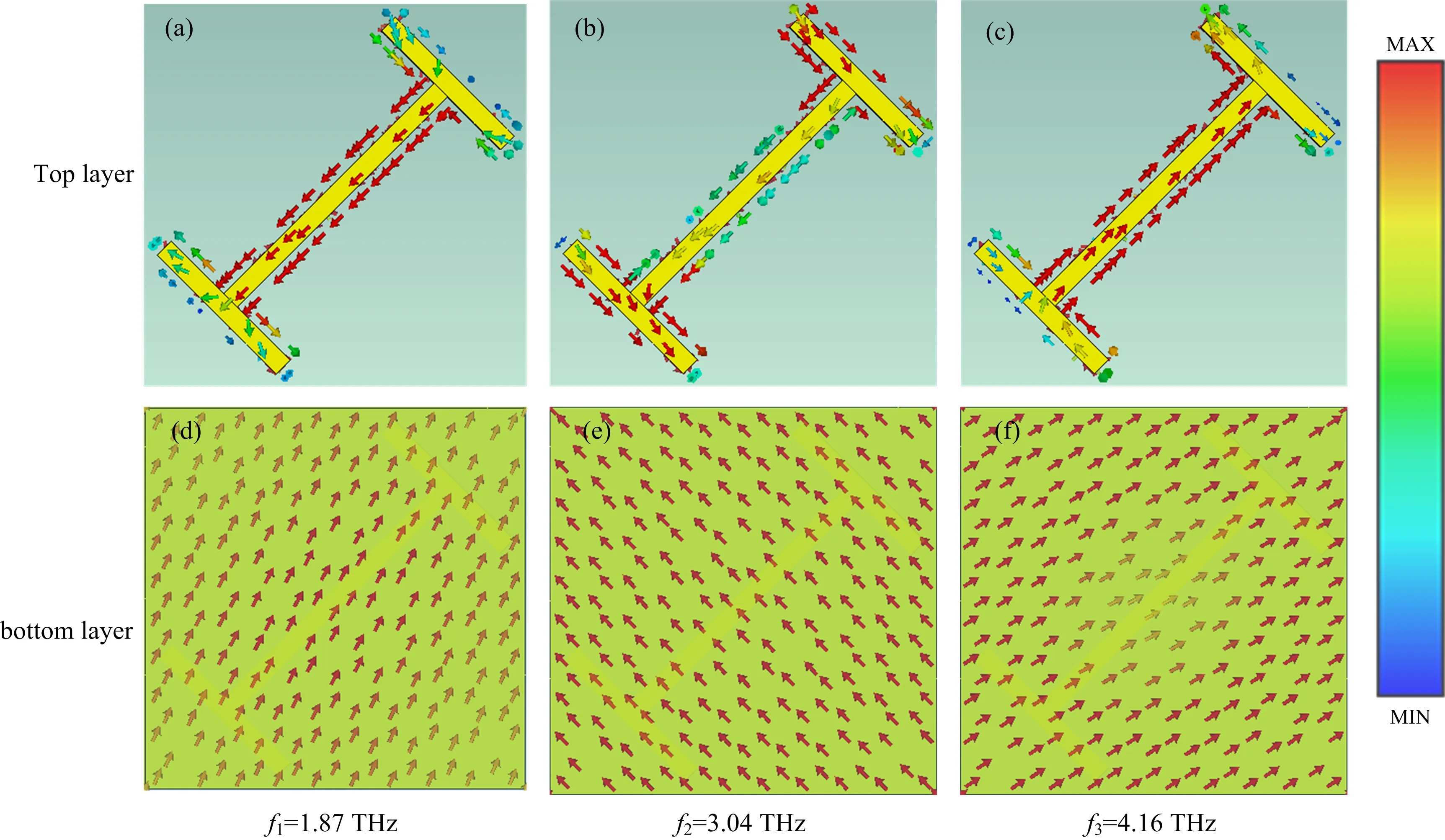
图3 当石墨烯的费米能级为0.1 eV且二氧化钒电导率为200 000 S·m-1时,f1=1.87 THz,f2=3.04 THz,f3=4.16 THz处的顶层和底层表面电流分布
为了探究该超材料吸收器的各个组成部分对结构吸收性能的影响,分别对去掉顶层二氧化钒谐振层、去掉底层金属板以及顶层二氧化钒谐振层与底层金属板同时存在时吸收器的吸收性能进行了仿真分析。 如图4所示,当去掉顶层的二氧化钒谐振层时,吸收率仅有1.6%,电磁波几乎全部被反射。 当去掉底层金属板时,该频段内的吸收率达到46%,当顶层二氧化钒谐振层与底层金属板同时存在时,吸收率明显提高且吸收率超过90%的带宽达到了2.8 THz。 这说明发生完美吸收的主要原因是底层金属板的存在,阻止入射波发生透射,且顶层谐振单元的存在,能够更好的让入射电磁波消耗在吸收器的内部,增强了吸收率并扩大了吸收带宽。

图4 不同结构的吸收光谱Fig.4 Absorption spectra of different structures
此外,分析了石墨烯表面电导率的变化对所设计结构吸收性能的影响。 石墨烯的表面电导率与其费米能级有关,因此可以通过施加偏置电压来动态调节石墨烯的费米能级和表面电导率,从而实现吸收频带的动态调谐功能。 如图5所示,展示了吸收器结构在不同费米能级下的吸收光谱。 当石墨烯的费米能级由0.1 eV增加到0.3 eV时,相应吸收频带逐步向更高的频率区域移动,同时吸收峰的带宽逐渐减小,但幅值基本保持不变。 这是由于石墨烯费米能级改变,其表面电导率也随之改变,破坏了吸收器的阻抗与自由空间的阻抗匹配,导致产生了不同的吸收光谱。 然而,即使石墨烯的费米能级为0.3 eV时,该超材料吸收器吸收率超过90%的带宽仍然达到1.37 THz。
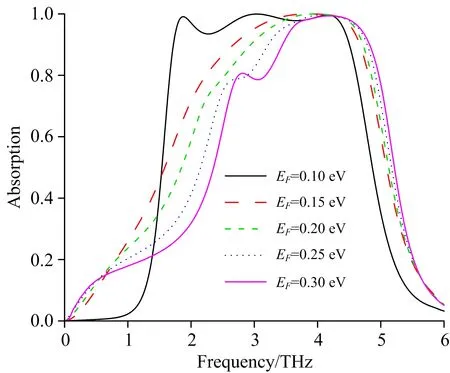
图5 不同石墨烯费米能级下超材料吸收器的吸收光谱Fig.5 Absorption spectra of metamaterial absorbersunder different Fermi levels of graphene
详细研究了顶层二氧化钒材料电导率变化对吸收器吸收性能影响。 当石墨烯费米能级设为0.1 eV时,二氧化钒的电导率从100 S·m-1增加至200 000 S·m-1时的吸收光谱如图6(a)所示。 从图中可以看到,当二氧化钒的电导率为100 S·m-1时处于绝缘态,此时吸收器可以被认为是由石墨烯-介质-金属三层结构组成的“三明治”结构且吸收率仅有2.6%,几乎处于全反射状态。 而当二氧化钒电导率为200 000 S·m-1时处于全金属态,在相同吸收带内吸收率增加到了90%以上,几乎处于全吸收状态。 因此,通过控制二氧化钒电导率,可使所设计的结构在宽频带内实现从全反射状态切换到全吸收状态。 另外,图6(b)和(c)分别展示了二氧化钒电导率为100和200 000 S·m-1时的电场分布俯视图。 当二氧化钒电导率为100 S·m-1时,工字型两端几乎没有电场分布。 这是由于二氧化钒处于绝缘态,入射波入射到结构时,完全透过顶部的谐振层,而在底层金属板的作用下几乎全部被反射,导致了较低的吸收率。 当二氧化钒电导率为200 000 S·m-1时,谐振单元表面电场集中于工字型两端,电偶极共振以及相邻谐振单元之间的耦合提高了该吸收器的吸收率,实现了吸收率的动态调谐。
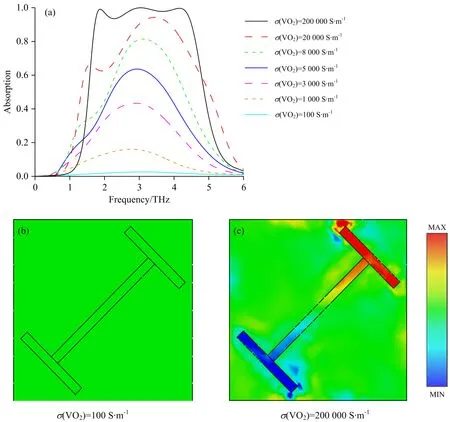
图6 (a)不同VO2电导率下超材料吸收器的吸收光谱;(b)当二氧化钒电导率为100 S·m-1时,3.04 THz处的电场强度分布俯视图;(c)当二氧化钒电导率为200 000 S·m-1时,3.04 THz处的电场强度分布俯视图
为了研究超材料结构的不同几何参数对吸收性能的影响,当石墨烯的费米能级为0.1 eV且二氧化钒材料电导率为200 000 S·m-1时,仿真研究了二氧化钒材料厚度T1及工字型中间条带长度L1对宽频吸收特性的吸收光谱。 如图7(a)所示,从图中可以看出二氧化钒材料厚度变化对吸收幅值及工作带宽具有明显的影响。 当二氧化钒厚度T1从0.1 μm增加到2 μm时,吸收率逐渐增强,吸收带宽也随之变宽。 如图7(b)所示,随着工字型结构长度L1增加,吸收带宽从1.76 THz逐渐增加至2.8 THz。
3 结 论
提出了一种基于石墨烯和二氧化钒的太赫兹宽带可调谐超材料吸收器结构。 研究结果表明,当石墨烯的费米能级为0.1 eV且顶层二氧化钒材料的电导率为200 000 S·m-1时,在1.70~4.50 THz宽频吸收带内获得了超过90%以上的吸收率,吸收带宽达到了2.8 THz。 当二氧化钒处于全金属状态时,调节石墨烯的费米能级在0.1~0.3 eV之间变化时,吸收率的中心频率发生了0.31 THz的蓝移。 当石墨烯的费米能级固定为0.1 eV时,利用二氧化钒的电导率随温度变化的相变特性,使其电导率从100 S·m-1变化至200 000 S·m-1时,该超材料结构由反射状态切换至吸收状态。 因此,基于所设计的超材料结构通过独立的调节石墨烯的费米能级和二氧化钒的电导率,可以实现超材料谐振频率与吸收振幅的双重调控。 此外,对超材料表面的电流与电场分布进行分析,揭示了超材料吸收器的吸收机理。 本文设计的可调谐宽带吸收器具有结构简单、吸收率高、谐振频率和吸收率可独立调谐等特点,在电磁隐身、移动通信、医疗传感等领域具有广阔的应用前景。
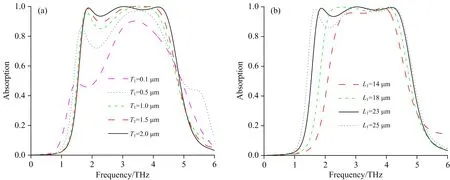
图7 不同结构参数对吸收器吸收性能的影响(a): 工字型厚度T1;(b): 工字型中间条带长度L1Fig.7 Influence of different structural parameters on absorber absorption performance(a): I-shaped thickness T1;(b): Length of I-shaped middle strip L1

