基于协变密度泛函理论的254 镄势能面的研究
陈盛远
(西南大学,重庆 400715)
原子核物理学的应用涉及到人类生活的各个方面,包括军事、能源、农业、医疗以及工业等,其发展给社会和人类文明带来了巨大的进步。原子核物理学为人类开启了一扇物理世界新的大门,其诞生的标志是卢瑟福于1911 年所做的α 散射实验[1]。之后,查德威克在1932 年又从实验上证明了中子的存在[2];同样在这一年,根据此实验,海森堡提出了构成原子核物质的假设,认为原子核是由质子和中子两种粒子组成的。而介子的存在则有汤川秀树于1935 年研究核力时提出。
20 世纪30 年代是原子核物理学快速发展的时代,对原子核物理学的研究也加深了人们对微观世界的认知,将其提高到了一个新的高度。费雷德克里·约里奥·居里和伊伦·约里奥·居里夫妇两人于1934 年在法国巴黎用钋产生的放射性射线α粒子轰击铝箔时发现了人工放射性的现象,他们基于此得到了第一个人工合成的放射性元素30P;恩利克·费米受此启发,与其合作者开展实验,利用中子来轰击铀元素,从而在实验中发现了几种不同的半衰期放射性,基于此,他认为成功合成了超铀元素。一直到1939 年,奥托·哈恩和弗里兹·斯特拉斯曼重复上述试验后才观察到超铀实验的产物[3];同年2 月,莉泽·迈特纳和弗里施第一次将这种现象解释为原子核的分裂,即铀原子核发生断裂形成两个质量更轻的原子核,而非形成了费米所解释的超铀元素,这是人们第一次认识到原子核可以发生裂变从而形成完全不同的原子核。
原子核裂变过程是一个原子核分裂成两个或多个更小而质量更轻的碎片的核反应过程,在此过程中通常会产生自由中子和γ 光子,并释放大量能量。原子核裂变的发现为物理学研究开辟了一个巨大的研究领域,使人们对微观世界的认识有了进一步的发展。在“哈曼顿计划”支持下,一个最重要的应用便是由费米等物理学家提出的链式反应,基于此反应原理,人们通过核裂变的方式利用核能成为了现实。除了现实应用,原子核裂变对于微观世界的探索和理解起着举足轻重的作用,原子核裂变提供了一种新的方法来研究远离β 稳定线的奇特核性质[4],同时也是理解超重核合成过程的重要理论机制[5],并对天体物理中重核的形成[6]有着重要的影响。
原子核裂变是极其复杂的核过程[7],对人们理解微观物理现象起着巨大的作用。核裂变的理论基础是由尼尔斯·波尔和约翰·阿奇博尔德·惠勒基于原子核液滴模型研究原子核裂变过程所奠定的。原子核的表面振动能和核子间库仑能之间的相互作用形成所谓的裂变位垒,原子核裂变的发生需要其能量越过裂变位垒。原子核的裂变位能曲面能反映出裂变位垒的状况,对裂变碎片激发能、动能以及质量和电荷分布有着重要的影响,因此,原子核裂变位能曲面对于理解裂变机制以及各种裂变可观测物理量的性质有着决定性的作用。
原子核裂变一般发生在重核区,而此区域中的原子核包含着数百的核子,其通过多体相互作用耦合在一起,由于多体问题过于复杂,目前的计算机性能无法满足第一性原理计算(ab initio calculation)的需求,因此对于裂变系统的微观研究主要是基于原子核能量密度泛函理论(Density Functional Theory,简称DFT)实现的,故如何用能量密度泛函描述好静态裂变学性质就显得尤为重要。基于原子核能量密度泛函,利用含时坐标生成法(time-dependent generator coordinate method,简称TDGCM),加上高斯重叠近似(Gaussian overlap approximation,简称GOA)的方法可在完全量子化的条件下研究裂变现象。
基于上述方法,研究原子核裂变的第一步,就是构建相应的裂变位能曲面(potential energy surface),并提取相关的集体参量,如集体质量、集体坐标等,以及一些关于裂变性质的物理量,如剪裂线等。目前可以计算原子核裂变势能曲面的能量密度泛函包括非相对论能量密度泛函,如零程Skryme 能量泛函和有限程Gogny 能量泛函,以及相对论能量密度泛函,也就是协变密度泛函。
本文基于协变密度泛函理论,采用PC-PK1 参数的能量密度泛函,对相对论平均场进行多维约束计算,得到了包括势能曲面、集体质量以及剪裂线等物理量。在计算中考虑了Bardeen-Cooper-Schrieffer(简记BCS)近似,即在计算中考虑了对关联效应。
1 理论框架
本文采用点耦合泛函理论,详细计算了254Fm的势能面。工作中,笔者采用能量密度泛函PC-PK1[8]来决定粒子- 空穴道的相互作用,对于粒子- 粒子道,使用δ 力来进行计算。考虑到所计算的位能曲面是原子核形变参量质量四极和八极矩的函数,可以通过对质量四极和八极矩参量施加约束,计算得到从小形变区域到发生组态突变的大形变区域的势能面。计算中,使用二次约束方法,其函数形式为不受限变分:
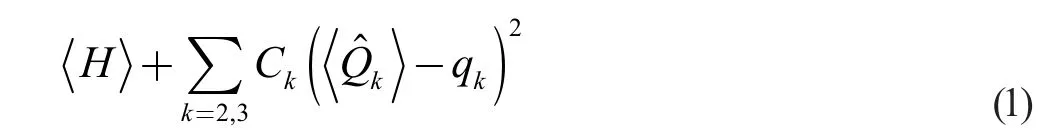
其中<H>为总能量,qk表示多极矩约束值,Ck则是对应的劲度系数, 而<>表示质量四极矩算符和八极矩算符的期望值,其具体表达式如下:
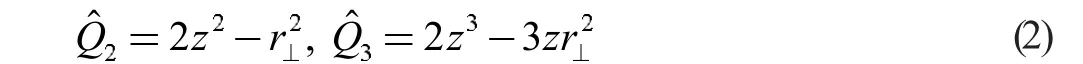
将上述多极矩期望值化为无量纲参数,为此引入对应的无量纲形变参量β2和β3,并通过下式进行转换:
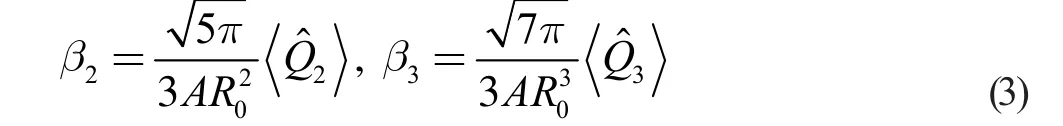
其中R0=r0A1/3为对应的球形原子核半径,一般取r0=1.2fm。
基于相对论平均场,加入Bardeen-Cooper-Schrieffer 方法,可以对方程进行约束自洽的求解,并获得单核子的能量、占据因子以及波函数,而这些物理量则可以进一步扩展至对原子核裂变的研究[9]。为获得单核子狄拉克方程的解,将在轴向形变的谐振子基上展开核子波函数。

其中:
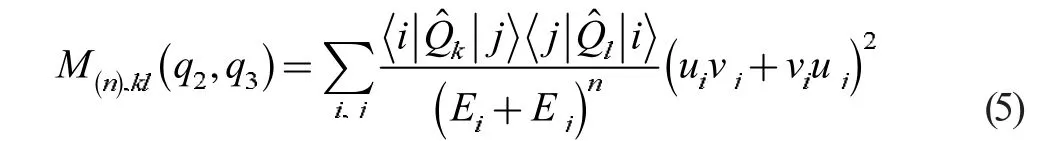
上式求和符号中的哑指标取遍所有的质子和中子的准粒子态。通过约束RMF+BCS的方法可求解得到准粒子占据几率vi、能量Ei以及单粒子态。
由于以上均为约束计算,没有考虑原子核的零点运动能,为此须引入转动以及振动零点能,可通过推转近似得到:
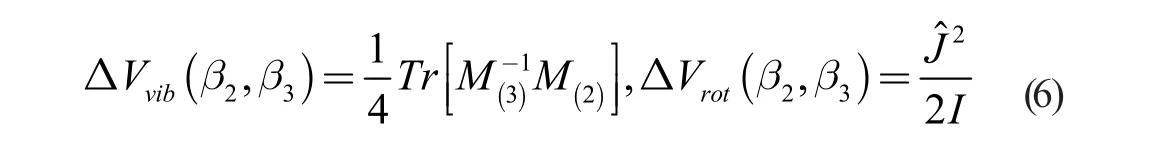
其中,I 为Inglis-Belyaev惯量矩。因此,所计算核的整体势能可由下式得到:
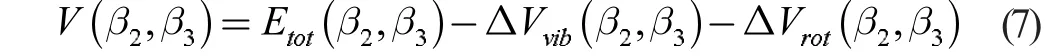
2 结论与讨论
此计算中,采用相对论平均场并引入BCS对关联效应计算了254Fm势能面,所用对力强度由五点耦合公式计算得到[9],所得到的中子和质子对强度分别为 Vn=317MeVfm3和Vp=348MeVfm3。对于单粒子波函数,可通过在柱坐标下展开轴对称形变谐振子基,自洽求解狄拉克方程得到[11]。计算中所用步长为Δβ2=0.04 和Δβ3=0.08。
图1 所示的势能面可分为两部分:一部分为内部区域,此区域中的组态表示原子核尚未发生断裂,为一个整体;另一部分为外部区域,这个区域表示原子核已经发生断裂,表征所有的断裂组态;这两部分由所谓的剪裂线连接,如图中的洋红色曲线,剪裂线在此计算中定义为粒子数为3 的位置,也就是当原子核某点的核子数密度小于3 时,便将其视为断裂组态。
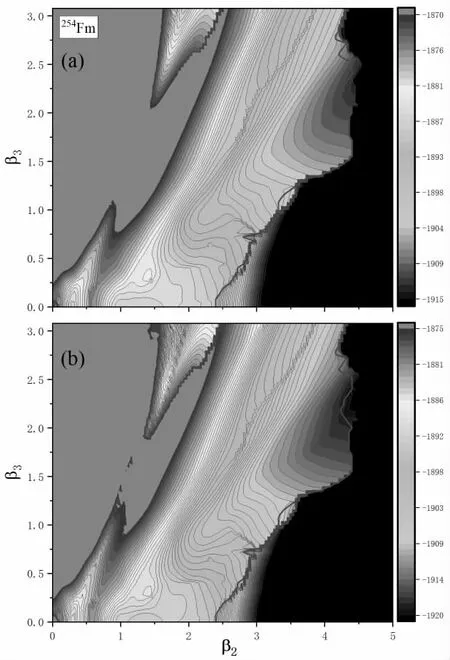
图1 相对论平均场+BCS 计算得到的254Fm 势能面。(a)未包含零点修正能的势能面,(b)包含零点修正能的势能面。洋红色表示剪裂线
图1(a)为采用RMF+BCS方法对质量四极矩和八极矩进行约束计算得到的不包含零点修正能的254Fm势能面等高线图,图1(b)则为加入了零点修正能后的254Fm势能面等高线图。洋红色线为剪裂线,组态在这个区域发生突变。
整个势能面的计算范围为β2∈[0,5],β3∈[0,3.08]。从图1可看出,在254Fm的计算中,是否包含零点修正能不会影响势能最低点的位置,计算得到的势能最低点均位于(β2,β3)~(0.28,0.00)处,在(a) 和(b) 中所对应能量值分别为-1886.0747MeV和-1890.42942MeV。对于(a),也就是未加入零点修正能的势能面,沿着对称裂变路径,即β3=0 方向,发现其具有双峰结构,第一个对称裂变位垒位于(β2,β3)~(0.56,0)区域,垒高10.52332MeV。之后势能迅速降低,再经过一段较为平缓的势能变化区域,在(β2,β3)~(1.76,0)区域出现第二个对称裂变位垒,此位垒垒高相对第一裂变位垒低得多,仅为0.45643MeV,当考虑如原子核裂变这样的大振幅集体运动时,此位垒对裂变过程影响较小,而且此区域与非对称裂变谷之间的连接呈现平缓的下降,可能对后期的动力学演化产生影响。对于(b),即加入零点修正能之后的势能面,可以看到,除了能量整体下降之外,其势能面整体趋势与(a) 一致,第一位垒同样位于(β2,β3)~(0.56,0)区域,高9.69405MeV,相对未加零点修正能而言,下降了0.82927MeV。由于裂变动力学对激发能依赖较大[10],而零点修正能包含了原子核的振动动能和转动动能,考虑到原子核裂变从受激发一直到发生断裂前都是一个缓慢的大振幅集体运动,若将其考虑成绝热近似,而且原子核在其平衡位置附近发生转动和振动,当进行动力学演化计算时,有必要考虑零点修正能对其过程的影响。需要注意的是,势能面上每个形变点的零点修正能不相同。
一个比较值得注意的现象是,沿着对称裂变道附近的剪裂线往外,能量并未发生突变,而是平缓降低。此外,笔者注意到在β2<3 区域,除去剪裂线,可以发现势能随着β3的增加而增大,这意味着当进行裂变动力学演化时,此处的势能将在很大程度上阻止原子核在这些组态上发生断裂。
在图1(b)中,从第一个裂变位垒出发,在1.5<β2<2.3 和0<β3<0.4 区域内,势能变化较为平缓,而且可以看出对称裂变路径比非对称裂变路径更短,而非对称裂变谷区域势能相对对称裂变谷势能更低。由于对称裂变谷和非对称裂变谷的特性,可能导致的结果是,在动力学演化中,原子核集体波函数以相当数量级的概率密度沿着对称裂变道和非对称裂变道扩散,且在演化的最终时刻在剪裂线的非对称裂变区域和对称裂变区域累计几近同等的通量,并最终表现为裂变碎片分布同时具对称裂变和非对称裂变模式。
原子核裂变的一些特征,如碎片质量、电荷等,在理论计算中表现在势能面上剪裂线区域。如图2 所示,画出了剪裂线上裂变重碎片质量随质量八极矩的分布。图中可看出碎片质量在(125.066,162.92)的范围内变化,而这将在后续动力学演化中的产物分布中有所体现。碎片质量整体上随着β3的增加而递增,这是很容易理解的,由于质量八级矩会使原子核在剪裂线处的组态表现为一轻一重的两个碎片,而随着β3的增加,这样的效果会更加明显。此外,在β3~1.5 附近,碎片质量分布呈现出局域的减小趋势,结合图1 可以发现,此处的β2变化较快,其作用恰好是让原子核在发生形变时趋于两碎片质量相等的组态,故此处表现为碎片质量随β3的减小。剪裂线处重碎片电荷随质量八极矩的分布如图3 所示。碎片电荷变化范围在(49.434,63.781)之间,整体趋势与碎片质量随β3的变化一致。需要注意的是,某个特定碎片的质量和电荷表现为图2 和图3 中同一β3所对应的值。
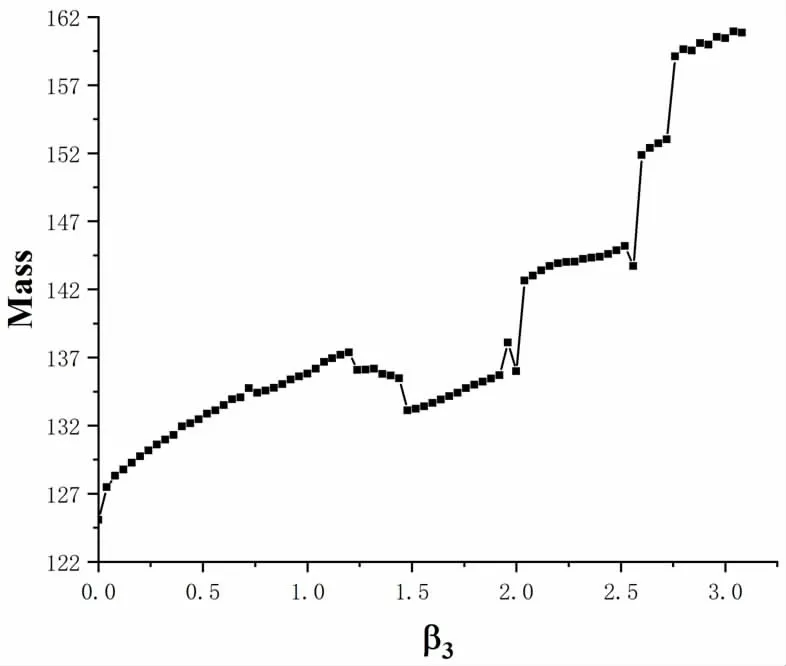
图2 剪裂线处重碎片质量随质量八极矩的变化
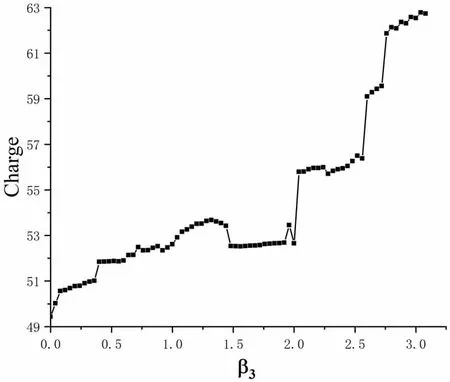
图3 剪裂线处碎片电荷随质量八极矩的变化
3 总结与展望
本文采用点耦合密度泛函理论模型,引入BCS 对关联效应,计算了254Fm裂变势能曲面并分析其相关性质,所得到的势能面第一裂变位垒较高,后续进行动力学演化时受此影响较大;而第二裂变位垒很低,对后续探讨影响不大。所得结果中,对称裂变道较短,非对称裂变道较长,但由于非对称裂变谷势能耕地,而且两者之间并无势垒将隔开,可能导致动力学演化得到的裂变产物分布呈三峰结构。由于原子核在其平衡位置附近发生转动和振动,故在进行裂变动力学演化时,势能面作为输入应包含零点修正能。分析了剪裂线处碎片质量、电荷分布,其整体表现为随β3的增加而增大,但在β3~1.5 处,由于β2的快速增加致使碎片质量和电荷呈减小的趋势。后续将进一步展开探讨对254Fm的裂变动力学研究,以期获得其裂变产物分布。
——《势能》

