赣江象山枢纽一期临时航道通航水流数值模拟应用研究

胡雨涵，王志超，郝嘉凌，黄志文，李孜成

（1.江西省水利科学院，江西 南昌，330029；2.河海大学，江苏 南京，210098）

0 引言

赣江抚河下游尾闾综合整治工程由赣江下游尾闾综合整治工程、抚河下游尾闾综合整治工程以及河湖水系连通工程三部分组成。赣江下游尾闾综合整治工程位于江西省南昌市，工程的主要目标任务为建闸抬水，从而改善水环境水景观，改善通航条件，促进城市和旅游发展。其中南昌市水利枢纽工程是以上综合整治工程的重要环节之一，是赣江下游尾闾综合整治控制性工程。本文针对其中主支上的象山枢纽施工一期临时通航水流条件问题展开研究。

目前，在对通航水流条件问题的研究中，物理试验和数值模拟法应用较多。与物理模型试验相比，数值模拟具有经济、快速、修改方便等优点，并且不受比尺的限制[1]，近年来国内外学者在数值模拟技术研究和应用方面均有长足的进展和丰富的成果。刘晓东[2]等人建立了基于四叉树网格的二维水流数学模型，实现了边界和重要研究区域的网格加密，并在其基础上较好地模拟了太湖边界的复杂流场和浓度场，此外模型还具备了节约计算时间，数据结构较为简单等特点。刘新成等[3]人利用三角形网格进行河网概化，并在此基础上建立二维有限元潮流数学模型，成功模拟了长江口和杭州湾潮流场，进而又对长江口和杭州湾交汇处水体交换的范围进行了定量计算。陈青毅等[4]人采用三维浅水方程和物质扩散方程模拟了河口水库流态，根据长江口青草沙水库工程的初步运行方案，计算了不同风场条件和水库引排水条件下库区的流场。黄牧涛等[5]人采用三角形网格和垂向σ坐标进行河网概化，建立了湖泊三维水动力数学模型，并采用显隐结合的方法求解三维水动力方程组。随着科学技术的发展，水动力数值模拟方法必将朝着更高精度和更高效率方向发展。

鉴此，本文应用水动力数值模拟技术，建立象山枢纽施工一期工程的平面二维水动力数学模型，计算分析不同水位流量边界条件下施工河段的水流特征，为工程施工导流期间的临时通航提供技术支撑。

1 工程概况

象山枢纽建于赣江下游尾闾河段主支之上，位于江西省南昌市新建区象山镇鸭洲村附近，距象山镇6 km，距南昌市约35km，主要任务是调控赣江下游尾闾河段的枯水期水位，改善水环境和水景观等问题。主体工程于2021年2月开工建设，计划2026年完工。主支南昌～湖口段航道现状等级为Ⅱ级，全年通航，施工期间需维持正常通航，因此，施工期通航问题是枢纽施工方案的重要内容之一。

1.1 总平面布置

象山枢纽主要由泄水闸、船闸、鱼道、泄水闸与船闸连接段和两岸上下游连接堤防组成。河床布置泄水闸，中部布置大孔闸，左岸布置鱼道，右岸布置船闸，两岸退建和加固堤防与现有堤线连接。

根据地形地质条件、水文及施工因素，本工程施工方案分两期施工。其中一期工程施工方案为先疏浚左侧滩地，待左侧滩地具备通航条件，在一期围堰保护下施工右侧泄水闸和船闸，预计26个月完工，施工洪水标准为10年一遇。一期工程施工平面布置见图1。

图1 一期工程施工平面布置

1.2 通航方案

一期工程施工临时航道进出口与现有航道连接，临时航道最小弯曲半径690m，航道底高程4.0m，最低通航水位7.90m。临时通航期间流速、流态应满足自航条件。依据GB50139－2014《内河通航标准》和赣江代表船舶特征，航道最大纵向流速应≤2.0m/s、横向流速应≤0.3m/s、回流速度应≤0.4m/s、水深应≥2.8m。

2 数值研究

2.1 基本原理

本研究采用DHI MIKE软件进行水动力计算，当中的MIKE21 FM模块采用了基于非结构网格的有限体积法对平面二维水动力方程进行离散求解，针对不规则岸线问题时有较好的拟合效果。此外MIKE21 FM在水动力基本方程中考虑的因素比较全面，所以目前应用广泛[6～9]。当不考虑源汇项、风场作用、地球自转、波浪影响、密度变化等因素，则水动力基本方程可为以下形式：

连续方程：

动量方程：

式中：t为时间，s；z为水位，m；d为静止水深，m；h=d+z为总水深，m；、分别为x、y方向上的沿水深平均速度，m/s；g为重力加速度，m/s2；ρ为水的密度，kg/m3；τb为壁面剪应力，N/m2；Tij为水平剪切力项，包括粘性力、紊流应力和水平对流，其中v 是水平涡流粘度，m2/s。

将控制方程转换成Godunov格式然后用有限体积方法离散，采用Roe格式的近似Riemann解计算界面通量[10，11]。

2.2 网格划分

采用非结构化网格，将工程大堤和围堰作为网格剖分的边界约束条件进行网格划分，共划分9 756个网格，网格平均面积为600m2，计算区域以非结构三角形网格为主，利用矩形网格对航道区域进行加密，模型网格布置见图2。

图2 施工一期模型网格布置

2.3 边界条件

洪水条件上边界采用外洲1月～4月各月洪峰流量频率计算成果，下边界采用当日外洲站日平均流量与设计流量相近时闸址最低日平均水位；枯水条件下边界采用主支闸址2003-2018年1月、2月、3月和4月的各月最低水位，上边界流量采用闸址水位与该最低水位接近时的闸址最大流量，具体见表1。

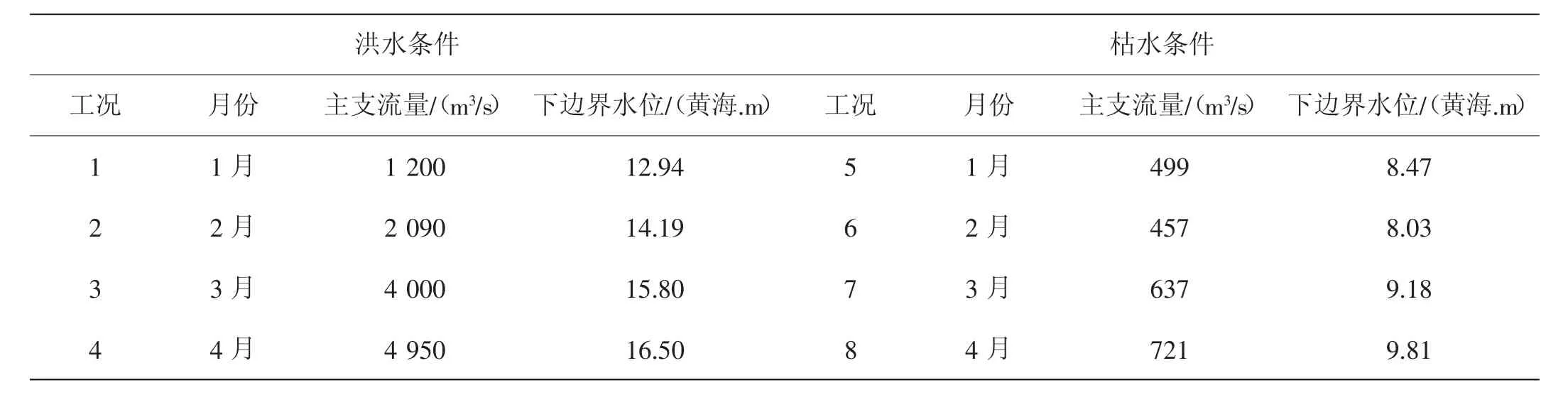
表1 航道流态模拟计算边界条件

3 计算结果分析

在临时航道区域坝轴线上下游距离4.5km范围内布置15个流速监测点如图3所示，提取各点水位和流速特征值，如表2所示。各水流工况下，临时航道水流特征基本符合流量大则纵向流速和横向流速大的规律，最大纵向流速为1.62m/s，最大横向流速为0.26m/s，最低水位为8.70m，均满足临时通航对水深、流速的要求。

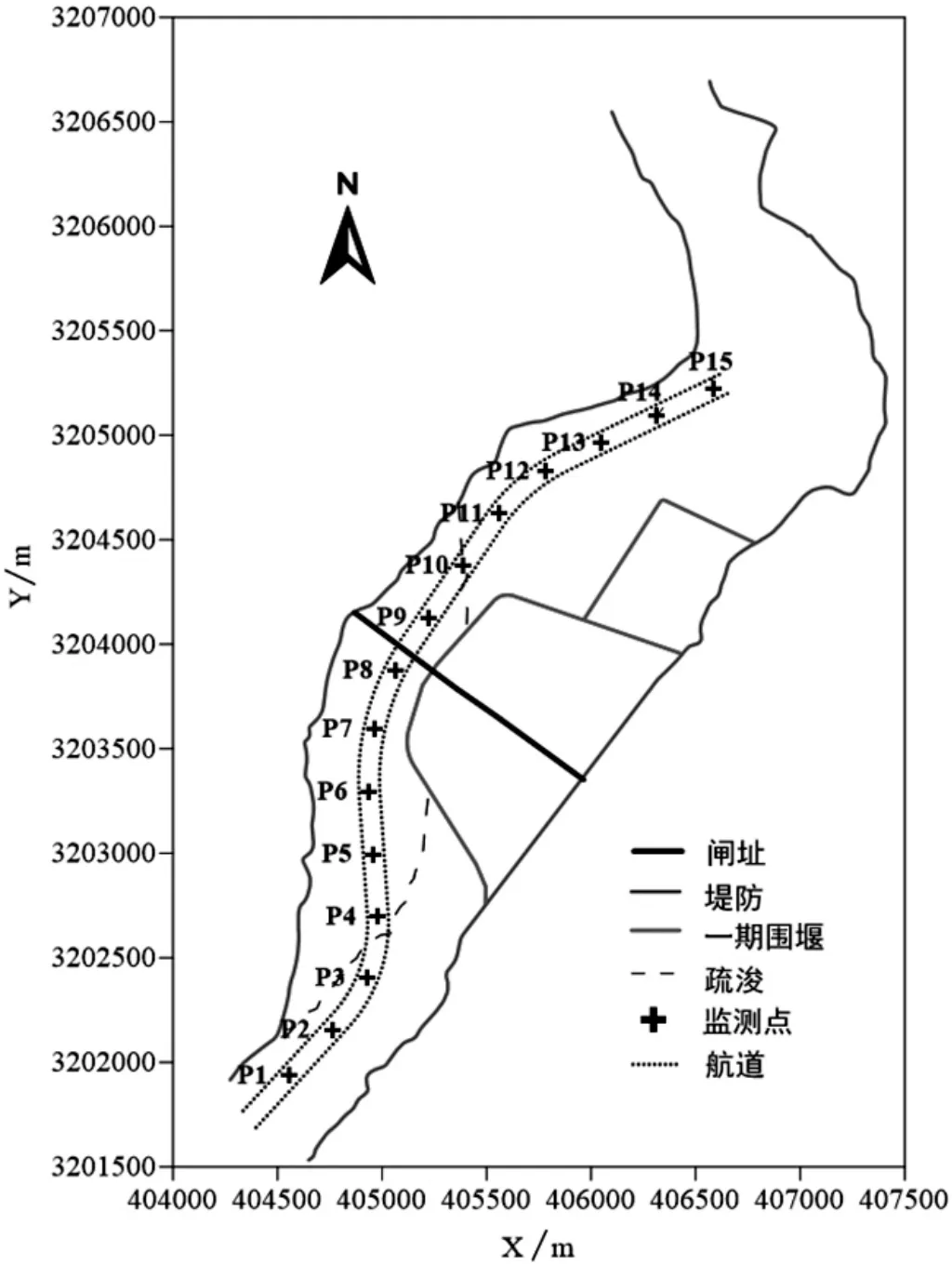
图3 航道流速监测点分布示意图

表2 临时航道的水流特征值

因工况4各项流速特征值最大，故以该工况为例展开临时航道流态分析，其监测点流速特征值和流场图分别如表3和图4所示。沿临时航道，流速分布特征为先大后小再增大，横向流速先小后大。临时航道入口流速为1.39m/s，由于下游河道渐宽，P1至P5河段流速逐渐减小至1.08m/s。下游河段由于围堰导致的河道缩窄，同时缩窄后水面坡降增加等因素，P6至P15河段航道流速整体上呈增加趋势，出口附近最大流速为1.64m/s。临时航道入口附近横向流速较小，横向流速较大的点主要分布在航道转弯段附近，如监测点P4、P6、P9、P11、P13、P14，绝对值在 0.10m/s至 0.15m/s之间。临时航道出口下游衔接向左岸的转弯河道，因此临时航道出口横向流速较大，监测点P15具有0.26m/s偏向左岸的横向流速。

表3 工况4各监测点流速特征值

图4 工况4流场图

4 结论

（1）经对施工一期临时航道水流条件展开计算分析，结果表明，各水流工况下，临时航道水流特征基本符合流量大则纵向流速和横向流速大的规律，最大纵向流速为1.62m/s，最大横向流速为0.26m/s，最低水位为8.70m，均满足临时通航对水深、流速的要求。

（2）沿临时航道，流速分布特征为先大后小再增大，横向流速先小后大。临时航道入口附近横向流速较小，横向流速较大的点主要分布在航道转弯段附近。临时航道出口下游衔接向左岸的转弯河道，因此临时航道出口横向流速较大。

（3）数值计算进行了概化处理，施工过程为动态变化过程，建议加强水流监测，根据实际情况适当调整航迹线。