钢筋套筒灌浆连接受拉性能数值模拟

周文轩

（上海公路桥梁（集团）有限公司，上海 200433）

0 引言

随着我国产业结构的升级，可持续化发展理念的不断贯彻，我国的建筑行业迎来了巨大的变化。传统的建筑施工方法资源消耗大、建设周期长、容易造成环境污染问题。装配式建筑的引入为建筑行业注入了新的活力，并得到了国家的大力支持、行业的普遍认同。

套筒灌浆连接是装配式建筑中最常用的一种连接方式，使节点接缝具有与现浇混凝土梁相同的整体性能[1-2]。套筒灌浆的基本原理是在钢筋套筒内注入高强早强微膨胀的灌浆料，待其硬化后，将两端钢筋连接成一个整体，通过材料间粘结力、机械咬合力传递构件中的作用力。现有的钢筋套筒通常为全灌浆套筒和半灌浆套筒两种类型，因为直螺纹端连接所需的钢筋锚固长度相较于灌浆连接所需较少，所以半灌浆套筒的接头尺寸较小。套筒灌浆连接的力学性能主要受钢筋、灌浆料、套筒的强度，钢筋的锚固长度等因素的影响。在施工过程中，如果存在非正常灌浆作业，使用水泥净浆替代灌浆料，使用高水灰比灌浆料容易产生钢筋刮犁式拔出破坏，灌浆料离析等非正常破坏[3]。毛诗洋等[4]通过反复拉压荷载试验研究了地震作用对不同饱满度灌浆套筒接头力学性能的影响，验证了灌浆不饱满会削弱灌浆套筒的力学性能。王占文等[5]通过单向拉伸试验研究了二次补浆量对半灌浆套筒连接性能影响，分析试件破坏形式、极限承载力、应变分布等参数，研究表明二次补浆可用于工程中，但不宜多次补浆。王凤等[6]基于室内试验和ANSYS 模拟研究表明灌浆料龄期对钢筋套筒的接头承载力和变形性能都有较大的影响。陈建伟等[7]设计并制作了6 组半灌浆钢筋套筒试件，研究了钢筋偏心缺陷对套筒受拉性能的影响，并使用ABAQUS 进行数值模拟和参数分析，模拟结果与试验数据吻合度较好，验证了模拟的可靠性。吴小宝等[8]研究了龄期和钢筋种类对套筒连接性能的影响，并进行单向拉伸和单向重复拉伸试验，研究表明龄期对钢筋的非弹性变形和总伸长率有较大影响。段文峰等[9]采用有限元软件提出一种基于全实体单元模型的显式动力分析方法，进行了相应的参数分析。

综上所述，众学者通过室内试验对套筒灌浆的单向拉伸力学性能已做了大量研究，得到大批可靠试验数据，但室内试验的成本高、不确定因素大。借助数值模拟可进行系统的参数分析，与试验结果相互印证，鉴于此，本文对已有试验的4个套筒灌浆使用ABAQUS 建模，与试验结果对比，验证模型的可靠性，并进行了进一步的参数分析。

1 试验概况

以吴小宝[8]进行的36个试件单调拉伸和单向重复拉伸数据为参考，选取其中4 组，建立了4个灌浆套筒钢筋连接试件，试件具体参数如表1，套筒模型示意图如图1所示。

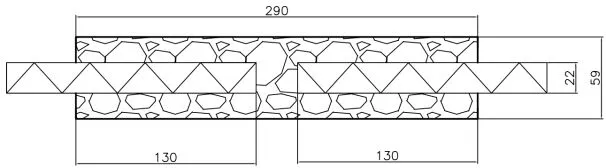
图1 钢筋套筒尺寸示意图Fig.1 Schematic diagram of steel sleeve size

表1 试件参数Table 1 Specimen parameters

套筒的屈服强度应力和极限应力分别391 MPa和534 MPa，弹性模量E为2.06×105MPa，伸长率21%，灌浆料龄期28 d的抗压强度和抗折强度分别为63.9 MPa 和6.33 MPa，弹性模量E为2.35×104MPa。

2 数值模型

2.1 材料参数

2.1.1 灌浆料

由于目前尚无灌浆料成熟的应力应变关系模型，而混凝土和灌浆料有一定的相似性，故选用混凝土的本构模型来模拟。在ABAQUS 软件中自带有混凝土塑性损伤模型（Concrete Damaged Plasticity Model，以下简称CDP），此模型假定了混凝土材料为连续介质，在受压应力下直至拉伸开裂或压缩破碎的损伤破坏都是各向同性的，混凝土材料的屈服面或者破坏面的演化用两个硬化变量来控制，此模型适用于显性求解分析，因为同时考虑了拉、压塑性应变导致的弹性刚度的退化以及循环荷载作用下刚度的恢复，具有较好的收敛性，其拉伸状态下的单轴应力—应变关系曲线表达式如下[10]：

式中：σt为拉伸应力；dt为混凝土材料的单轴拉伸损伤演化系数；E0为初始弹性模量；εt为拉伸应变；εplt为混凝土拉伸塑性应变。在建模过程中，使用的CDP塑性模型参数如表2所示。

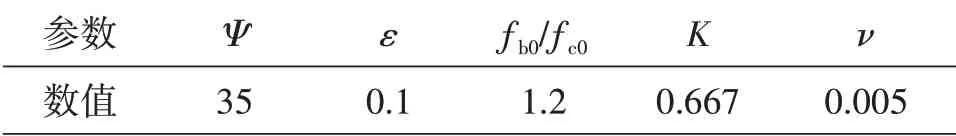
表2 CDP模型塑性参数Table 2 Plastic parameters of CDP model

其中，Ψ为膨胀角；ε为流动势偏移量；ƒb0/ƒc0为双轴受压与单轴受压极限强度比；K为不变量应力比；ν为粘滞系数。

2.1.2 钢筋

钢筋的应力—应变关系曲线采用双折线模型。其屈服强度和极限强度根据试验确定，弹性模量取2.06×105MPa，泊松比取0.3。其本构关系如图2所示。

图2 钢筋的应力—应变关系曲线Fig.2 Stress-strain curve of the steel bar

2.1.3 套筒

在试验过程中，套筒都处在弹性状态中，所以采用理想弹塑性模型，套筒的弹性模量2×105MPa，泊松比取0.3。

2.2 有限元模型建立

在ABAQUS 模拟过程中，采用显示动力学（ABAQUS/Explicit）进行求解分析。显示动力学求解是对时间进行差分，不存在迭代和收敛问题，具有较好的稳定性。而若使用隐式分析求解，往往会因为材料的退化和失效等问题导致不收敛，所以显示动力学常被用来求解需要分成许多时间增量来达到高精度的高度动力学以及复杂的非线性问题。对钢筋、套筒、灌浆料的单元库类型选择显式，族为三维应力，单元控制均采用C3D8R单元（8 节点六面体线性缩减积分单元），此单元在弯曲荷载下不易发生剪切自锁现象，对位移的求解结果比较精确，且网格存在扭曲变形时，分析的精度不会受到太大的影响。为了确保模拟的精确度，对整个模型的网格采用扫略网格划分技术，网格尺寸5 mm。

在试验过程中，灌浆料的粘结力良好，无论是钢筋刮犁式拔出还是钢筋拉断，都没有发生灌浆料拔出破坏，所以将灌浆料与套筒，灌浆料与钢筋都设置为绑定约束。为了实现钢筋的单向拉伸，在上侧钢筋端部添加一个参考点，并将此参考点与钢筋端部设置为耦合约束。接着在此参考点上采用位移加载，位移加载与试验一致为20 mm。边界条件设置为下部钢筋端部完全固定，上部钢筋限制除了轴向外的其他两侧位移和转角。

为了更加贴近实际钢筋，增加钢筋与灌浆料的机械咬合力，在钢筋的两端各设置了三条肋。A1各部件与整体模型网格划分如图3所。

图3 A1试件部件与整体模型网格划分Fig.3 Mesh generation of component and whole model of A1 specimen

2.3 有限元模型验证

模拟结果中灌浆料粘结效果良好，钢筋拉断破坏均发生在套筒外，钢筋套筒的应力分布云图如同4所示。如图5、6所示，为A2和A4的荷载—位移曲线，由于原试验中钢筋的位移取的整个构件的总位移，而模拟中所测是一侧钢筋的位移，所以将试验测得的位移减半。由图可知，模拟所得曲线与试验测得曲线有相同的发展规律。在弹性阶段，试件模拟值与试验值基本吻合，呈直线上升趋势，达到屈服点后，经过一个短暂的屈服平台，进入强化阶段，继续上升后达到极限强度，随后荷载值开始下降。模拟值的屈服强度和极限强度都略高于试验值，模拟所得A2、A4 峰值荷载分别为241.27 kN 和255.23 kN 与试验结果误差为5.36%和2.5%。分析原因为现实情况下灌浆料会有细微的裂纹，导致粘结强度有微小的降低，其次单向拉伸试验中，拉拔过程会产生小偏心，进一步降低了钢筋的承载力。通过对比，验证了有限元模型的可靠性。模拟与试验结果汇总如表3所示。

图4 钢筋套筒应力分布图Fig.4 Stress distribution of steel sleeve

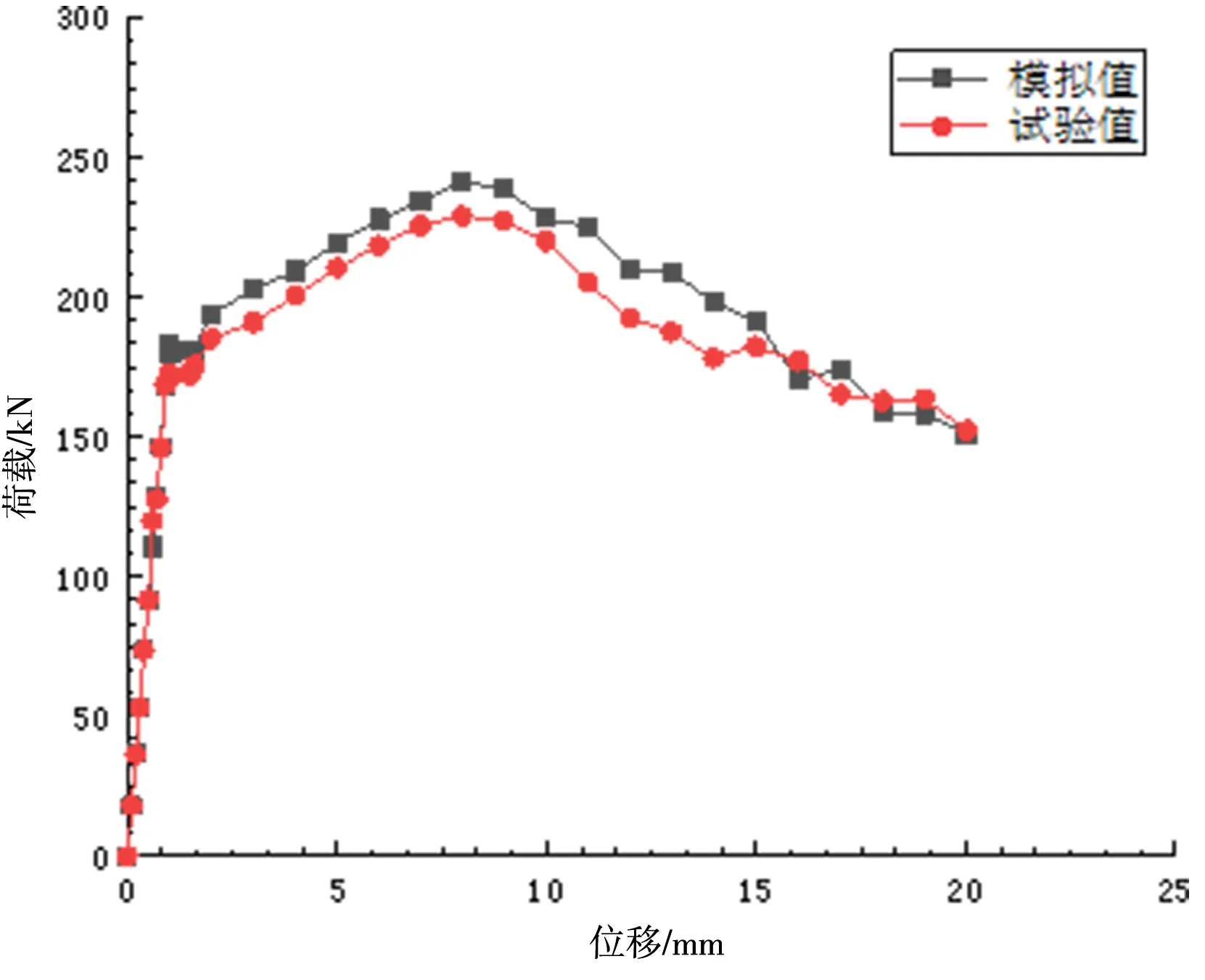
图5 A2试件模拟与试验结果荷载—位移关系曲线Fig.5 Load-displacement curve of A2 specimen simulation and test results

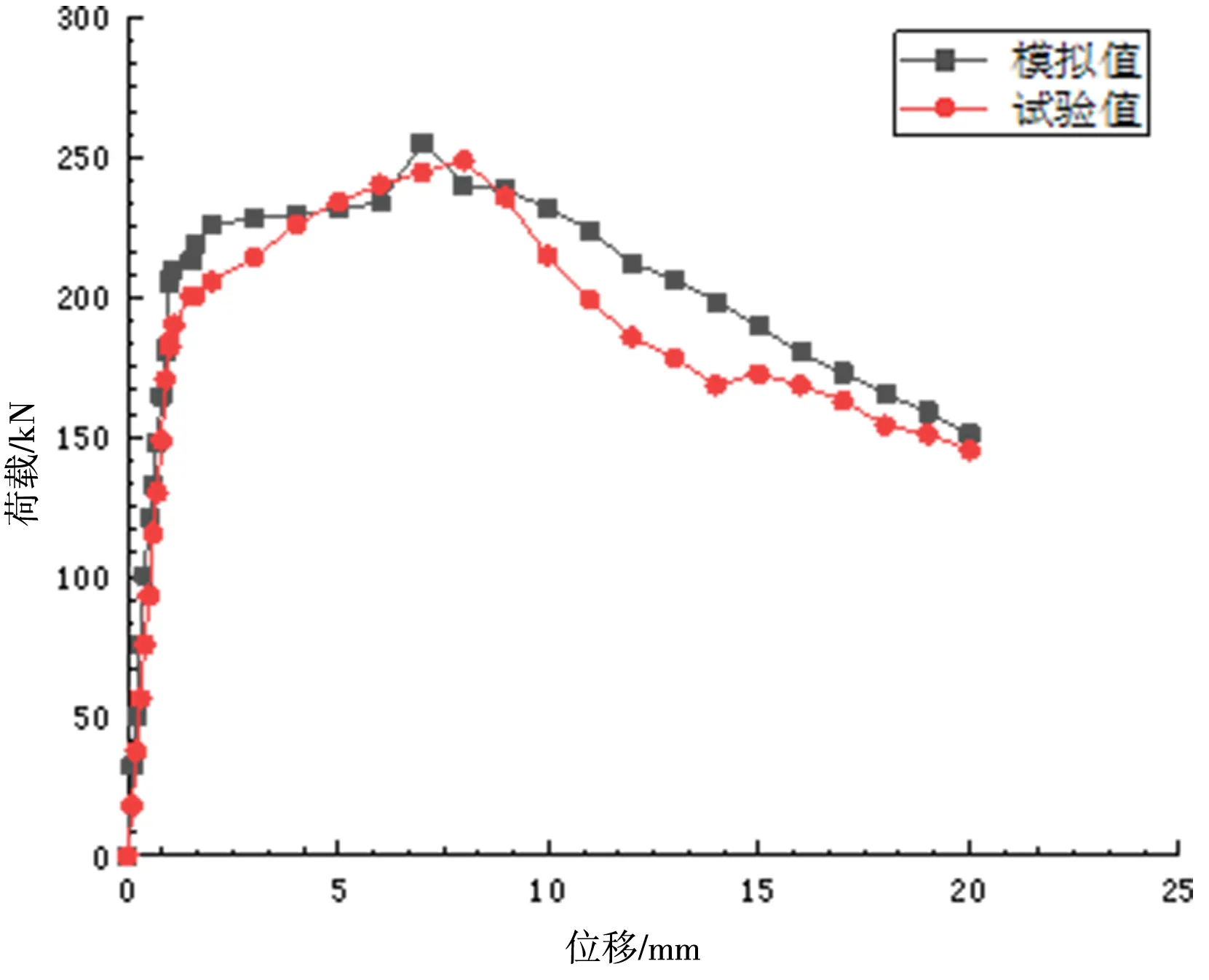
图6 A4试件模拟与试验结果荷载—位移关系曲线Fig.6 Load-displacement curve of A4 specimen simulation and test results

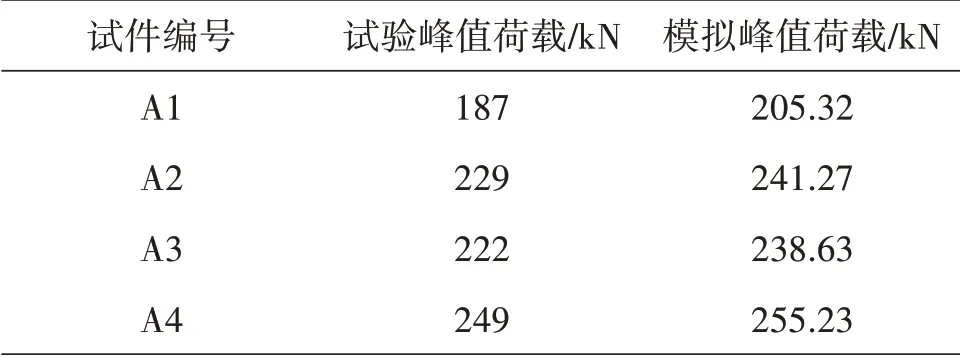
表3 模拟结果与试验结果对比Table 3 The comparison of simulation results and experimental results

2.4 灌浆缺陷破坏参数分析

在实际施工过程中，因为漏浆、少浆、回流等原因导致灌浆缺陷是比较常见的灌浆质量问题，灌浆不饱满是影响钢筋套筒的受力性能的重要因素。对A2、A4 试件分别模拟漏浆10%、20%、30%、40%四种情况，分析钢筋种类和灌浆不饱满程度对套筒连接力学性能的影响，灌浆不饱满的模拟通过改变钢筋的锚固长度来实现。由于灌浆不饱满，在单向拉伸试验中可能发生钢筋拔出破坏，所以将钢筋与灌浆料的绑定接触改为通用接触，将法向接触定义为“硬接触”；切向接触选用“罚接触”，摩擦系数为0.65，其荷载—位移曲线如图7所示。

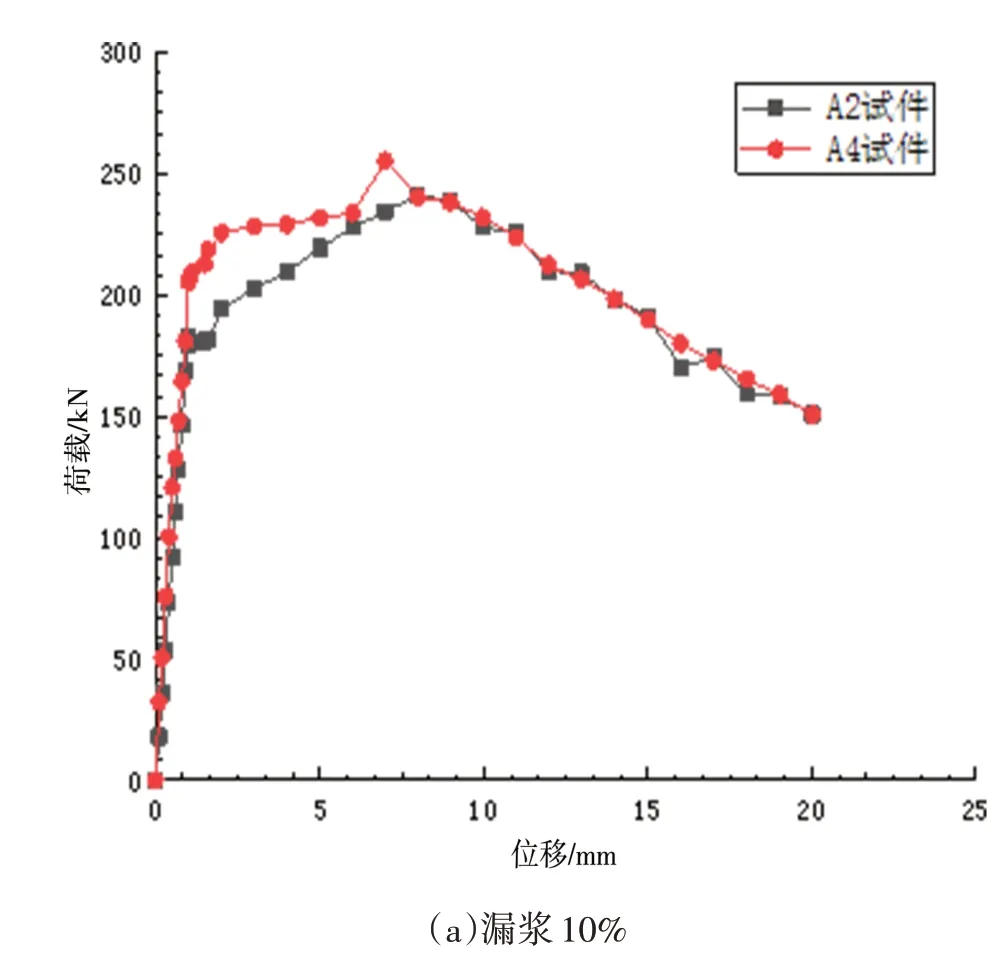
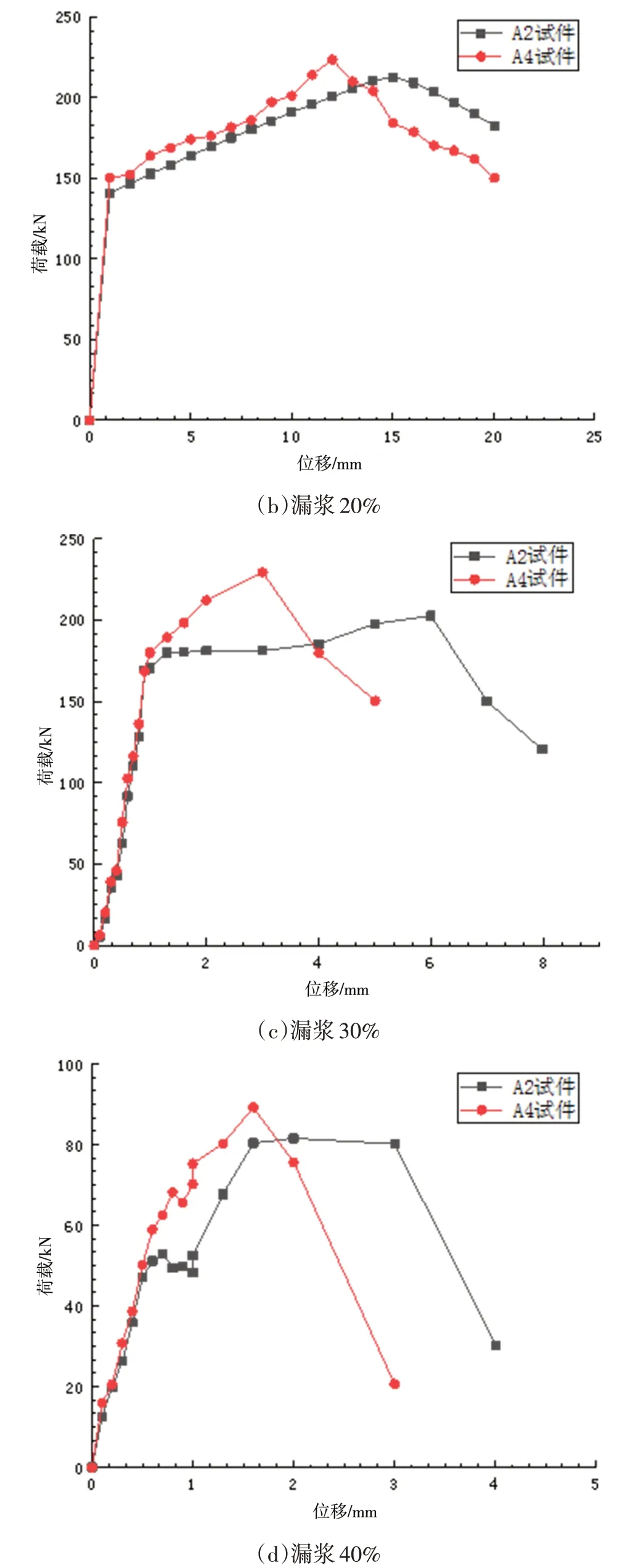
图7 不同灌浆缺陷下套筒荷载—位移曲线Fig.7 Load-displacement curve of sleeve under different grouting defects

漏浆10%时，荷载-位移曲线仍可分为弹性阶段、屈服阶段、强化阶段以及下降阶段，在套筒外的钢筋段发生颈缩后被拉断破坏，与灌浆饱满时的钢筋套筒力学性能基本一致。漏浆20%时，钢筋的强度超过了屈服极限，钢筋与灌浆料之间有微小的滑移使钢筋的极限强度有所降低，钢筋发生颈缩破坏，钢筋套筒的总体力学性能基本达标。漏浆大于等于30%时，钢筋的锚固长度少于5d，钢筋与灌浆料之间有明显的滑移，发生钢筋拔出破坏，其区别为漏浆30%时的钢筋依旧能达到屈服极限，但在还未达到极限强度前就被拉出破坏，而漏浆40%时，钢筋未达到屈服强度即被拔出破坏。对比HRB500 和HRB400 钢筋，相同直径的情况下，HRB500 钢筋的连接性能要高于HRB400，HRB400 钢筋与灌浆料的相对滑移要大于HRB500 钢筋，所以HRB500 钢筋会更快的到达极限强度，随后荷载值急剧下降，不过两种钢筋荷载—位移曲线总体的变化趋势相同。

3 结论

通过有限元软件ABAQUS，建立了灌浆套筒三维模型，并对单调拉伸试验进行数值模拟，验证模拟的可靠性后，分析了灌浆缺陷对套筒力学性能的影响，得出以下结论：

（1）数值模拟钢筋套筒灌浆单向受拉试验得到的极限抗拉荷载值会略小于试验所得值。

（2）钢筋套筒灌浆连接中，使用强度较高的钢筋可以获得更高的抗拉承载力。

（3）灌浆缺陷对钢筋套筒的受拉性能影响较大，当灌浆缺陷大于等于30%时，钢筋与灌浆料之间会产生明显的滑移现象，套筒受拉的荷载峰值急剧下降，并发生钢筋拔出破坏。