极震区烈度的ELM预测模型

郭少文，雷奇果，周 坤

（中交第二公路勘察设计研究院有限公司，武汉 430052）

0 前言

中国是世界上地震灾害最严重的国家之一，城市面临的地震灾害形势异常严峻。“5·12”汶川大地震、“4·14”玉树地震再次使人们认识到地震的强大破坏力。地震应急救援是防震减灾中的最后一道防线，其任务为高效、及时、有序地抢救生命，救助灾民，稳定社会和安定民心[1]。震后短时间内的地震灾情是地震应急快速响应与应急指挥的关键，但震后的地震应急灾情获取具有黑箱期效应，即震后短时间内地震灾情获取困难[2]。在地震灾后应急中，能快速获得极震区地震烈度则是应急指挥和救援的重要工作。地震烈度的研究最早始于1988年，Holder等[3]用关谷清景记录的20多条日本地震的主要振幅、周期，对比宏观现象后，估计了Rossi-Forel 烈度表（1883年，10 度表）中I 度到X 度的PGA。现行应用比较广泛的地震烈度评定标准主要有欧洲宏观地震烈度表（EMS-98）、日本气象厅（JMA）地震烈度表、Medvegev-Sponheuer-Karnik（MSK）烈度表、Modified Mercalli（MM）烈度表以及中国的地震烈度表等。中国地震烈度表的研究始于20 世纪50年代，1957年谢毓寿根据中国的房屋类型和震害特点，参照Medvegev 烈度表，编制了第一部《新的中国地震烈度表》[4]。本文以此为研究背景，收集了我国1966—2013年震级（M）＞5.0 以及2014—2017年部分历史地震数据，利用极限学习机（extreme learning machine，ELM）的回归拟合功能，以震级和震源深度作为输入参数对极震区烈度进行预测。

1 历史地震案例数据与处理

地震烈度是指某一地区的地面或各人工建筑物遭受地震影响的强弱程度[5]。极震区烈度是1 次地震引起的最大烈度，从地震地质角度看，极震区烈度受多个因素影响，如震源机制，地震波传播介质、路径，局部场地条件等[6]。本文收集的历史地震案例主要数据包括：地震发生时间、位置、震级、震源深度、极震区烈度等。

1.1 历史地震案例

收集了我国1966—2013年震级（M）＞5.0的部分历史地震数据（204例）以及2014—2017年部分历史地震数据（18 例），数据来源为中国地震局出版的《中国大陆地震灾害损失资料汇编：1966—1989》、《中国大陆地震灾害损失汇编：1990—1995》、《中国大陆地震灾害损失评估汇编：1996—2000》、《2001—2005 灾评报告汇编》、《2006—2010年地震灾评报告（综合稿部分20120330）》、《2011 灾评报告》、《2012灾评报告》、《2013灾评报告》和中国地震局官方网站公布的灾评通告，部分数据见表1。

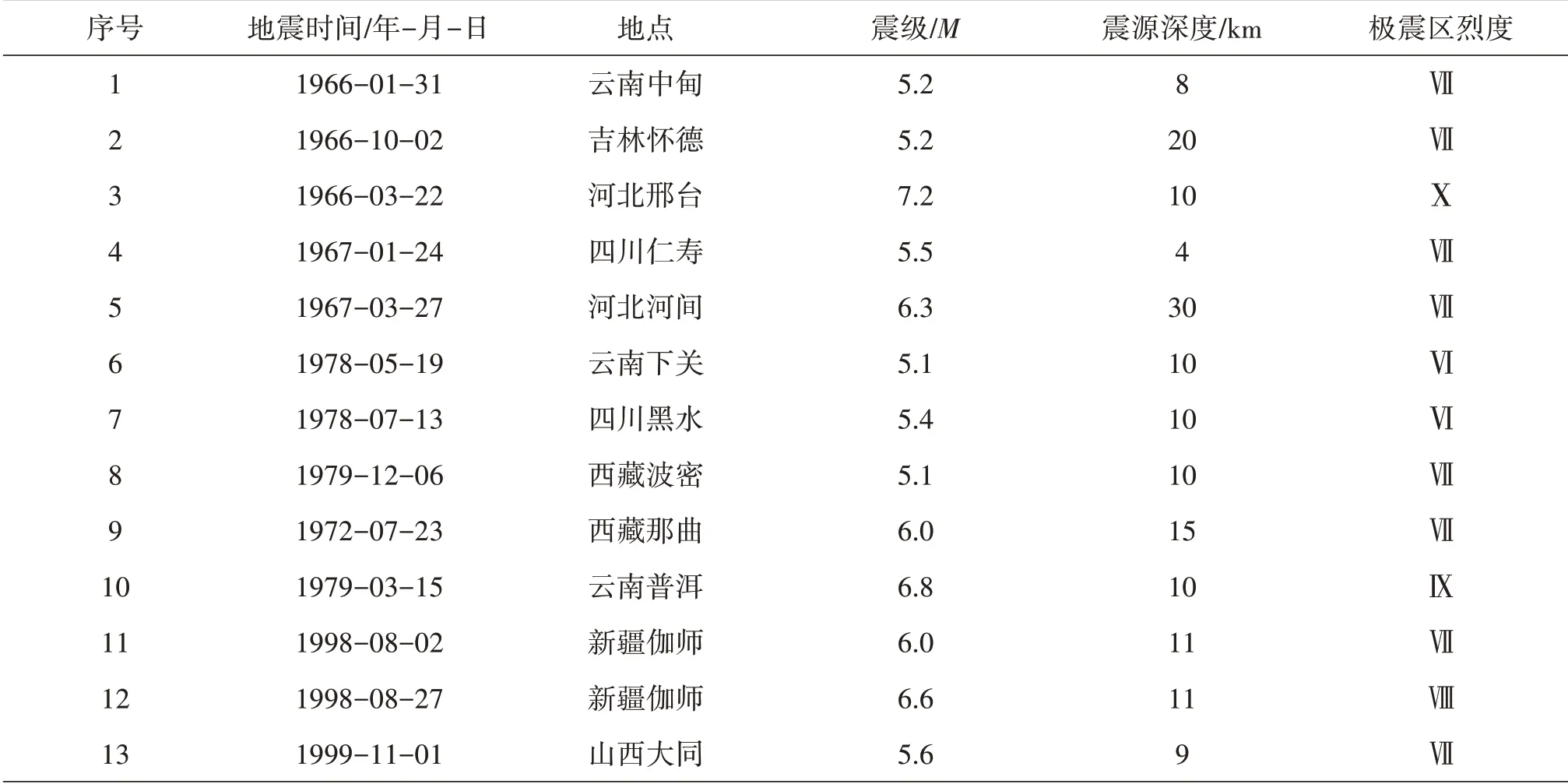
表1 部分历史地震案例数据Table 1 Data of the hisrorical earthquake

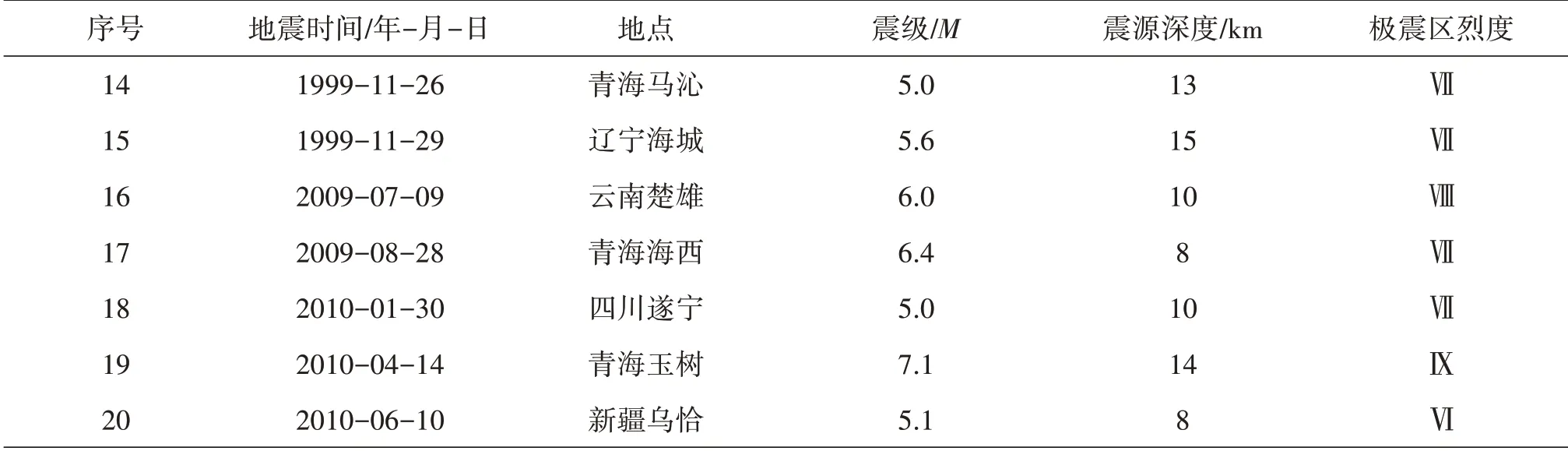
（接表1）

1.2 数据预处理

震级、震源深度和极震区烈度具有不同量纲，数值差别也较大。为了消除数据量纲和数值范围差异的影响，从而得到理想的模拟结果，必须将数据进行规范化处理，主要方法有最小-最大规范化、零-均值规范化、小数定标规范化，本文采用MATLAB自带mapminmax函数进行标准化处理，将原始数据值映射到[-1，1]，转换公式如下：

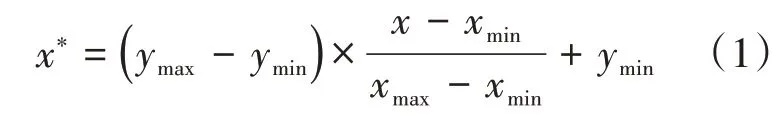
式中：x*为规范化结果，xmax和xmin分别为样本数据的最大值、最小值，ymax和ymin为映射函数参数，分别默认为1、-1。处理结果见图1。

图1 震级、震源深度和极震区烈度数据及规范化处理结果Fig.1 The normalized data of the magnitude，focus depth and intensity in meizoseismal area

2 ELM预测模型

Gutenberg 等[7]早在1942年就建立震级和极震区烈度的定量关系式M=2/3Ie+1；国内学者傅承义[8]于1960年提出M=（0.68±0.03）Ie+（1.39±0.17）logH-（1.40±0.29）；许卫晓[9]建立公式M=0.87Ie+0.8；随后，聂高众等（2018）对震级、震源深度和极震区烈度进行拟合分析后提出Imax=4.154 ＋0.113M2－0.0515H。以上诸式中，M为震级，Ie极震区烈度，H为震源深度。本文在上述研究的基础之上，采用ELM 方法利用震级和震源深度对极震区烈度进行回归拟合。

2.1 ELM原理

ELM 是Huang等[10]提出的单隐层前馈神经网络（single-hidden layer feedforward neutral net work，SLFN），因为其良好的学习能力在诸多行业领域中得到广泛的应用，与传统的训练方法相比，其具有学习速度快、泛化性能好的优点。

典型的单隐层前馈神经网络结构由m个输入变量，M个隐含层神经元，n个输出层神经元组成，其数学表达式为：

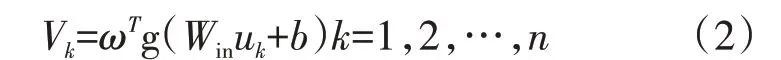
式中：Win为输入权值，ω输出权值，g为激活函数，通常取Sigmoid 函数，b为隐含层偏差值，n为样本总数，uk为m维输入向量，Vk为输出向量[11]。对n个样本对（ui，Ii），1≤i≤n，训练时输入权值Win 和偏差值b随机初始化并保持不变，只要训练确定的参数为输出权值ω，具体算法为：

式中，H+为隐含层输入矩阵H的摩尔-彭洛斯（Moore-Penrose）广义逆矩阵。I为期望输出矩阵，将H展开后，求出期望输出矩阵为[12]：

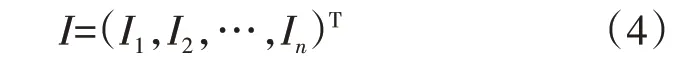
2.2 ELM模型建立与对比

2.2.1 ELM模型建立

在多个影响因素中，已有研究表明震中烈度与震级、震源深度之间存在关系是明确的[13]，通过震级和震源深度进行极震区烈度的预测是可行的。通过三者的三维趋势图（图2），可以看出震级和震源深度与极震区烈度分别为正相关和负相关性关系，即极震区烈度随着震级的上升而增加，随着震源深度的上升而下降。

图2 震级、震源深度和极震区烈度三维趋势图Fig.2 The three-dimensional trend chart of magnitude，focus depth and seismic intensity in the meizoseismal area

以震级和震源深度为研究对象，分析两者和极震区烈度关系并进行预测。选取204组历史地震案例数据，建立ELM 模型，步骤如图3。以MATLAB2013a 为平台编制ELM 程序，主要参数为：数据规范化函数mapminmax，ELM 训练函数elmtrain，预测函数elmpredict，激活函数hardlim。预测结果与真实值见图4，可以看出效果比较理想。

图3 模型建立步骤Fig.3 The process of model establishment

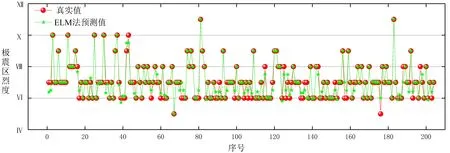
图4 ELM法预测值与真实值对比Fig.4 Comparison between the predicted value and real value of ELM method

2.2.2 ELM法与其它方法对比

为了检验ELM 方法的优点，将该方法与其它方法从定性和定量两方面进行对比。首先进行定性上比较，图5、6 分别为本文ELM 方法和文献1的线性模型方法与真实值的对比图，从两图中可以明显看出，ELM 方法预测效果更佳。然后从定量上比较，主要采用复相关系数R、决定系数R2、均方误差mse 三个拟合度参数进行对比，其中R2越接近1 说明拟合度越高，mse 越接近0 表明拟合效果越好。从表2 得出ELM 方法的拟合度参数有大幅提高，提高约20%。

表2 有效性参数对比Table 2 Comparison of effectiveness parameters

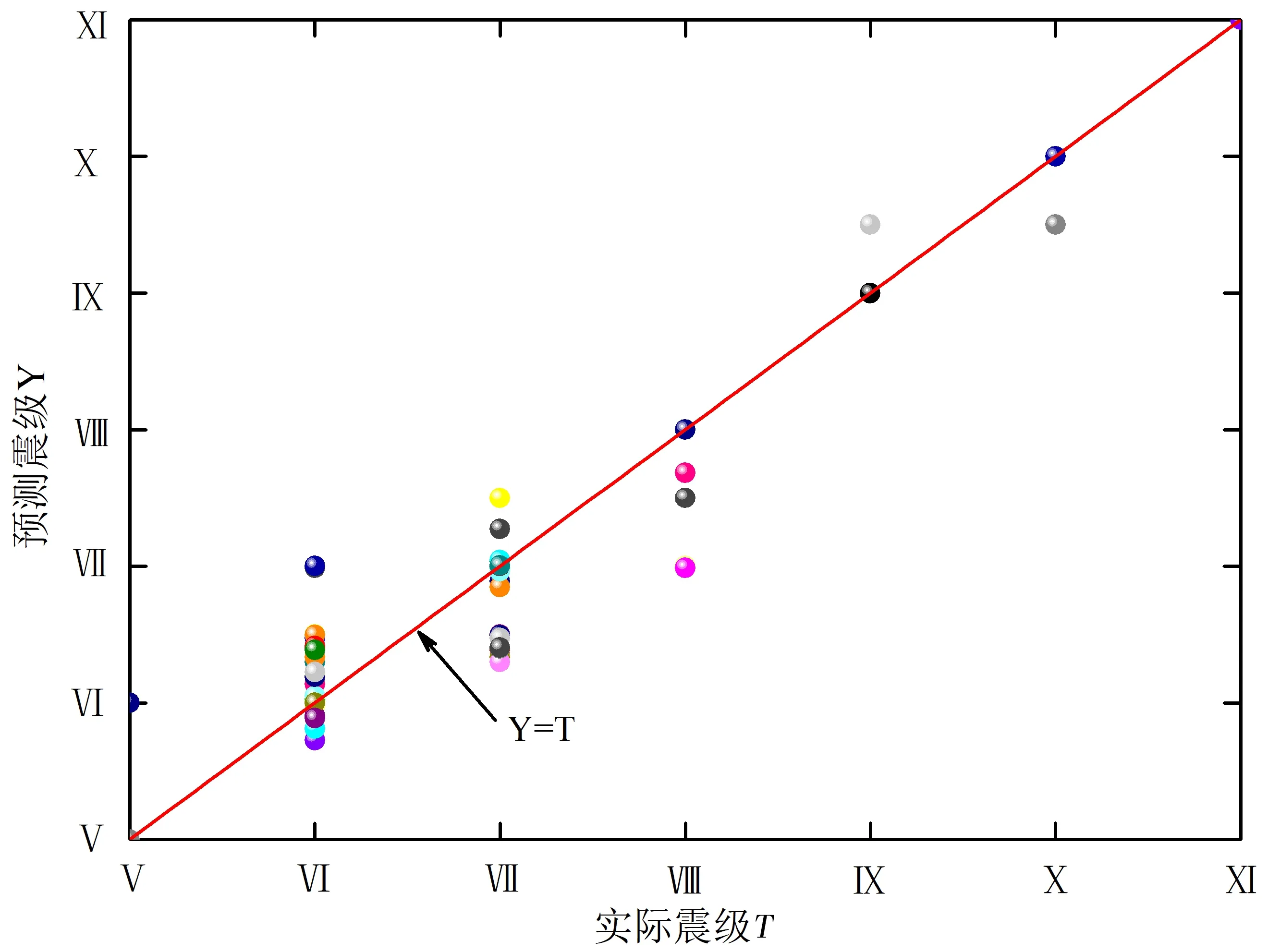
图5 极震区烈度ELM方法预测值与真实值对比Fig.5 Comparison between the predicted value and real value of ELM method in the meizoseismal area

图6 极震区烈度文献1方法预测值与真实值对比Fig.6 Comparison of the predicted value and real value of the method in literature 1 in the meizoseismal area

3 ELM模型应用与分析

3.1 ELM模型应用

为了检验模型在实际应用中的效果，对2013年以来发生的多次有感地震使用本模型进行极震区烈度预测。通过中国地震台网公布的地震速报信息，将地震震级和震源深度代入训练好的ELM模型，计算极震区烈度，结果见表3。

表3 模型预测结果和实际结果的对比Table 3 Comparison of model prediction of ELM results and real results

从该表中可以看出预测结果比较理想，但是新疆地区的预测结果偏差普遍较大，这可能是与该地区的场地条件、建筑物抗震能力有关，就需要今后多收集新疆地区的历史震例建立专门的预测模型。但不影响该模型的整体适用性。

3.2 参数权值分析

本文采用熵权法进行参数权值分析，熵权法是根据参数变异性的大小来综合确定客观权重。通常若某个参数的信息熵越小，其变异程度就越大，包含的信息量就越多，在评价中影响的程度就越大，其权重就越大；相反某个参数的信息熵越大，其变异程度就越小，包含的信息量就越少，在评价中影响的程度就越小，其权重就越小。操作步骤如下：

（1）数据标准化。对于参数Xj={X1，X2，…，Xn}按式（5）进行处理后得到Yj={Y1，Y2，…，Yn}。

（2）确定参数的信息熵。根据熵的定义，参数的信息熵Ej为

（3）确定参数的权重。对于k个参数，先计算各参数的信息熵Ej然后计算权重Wj为

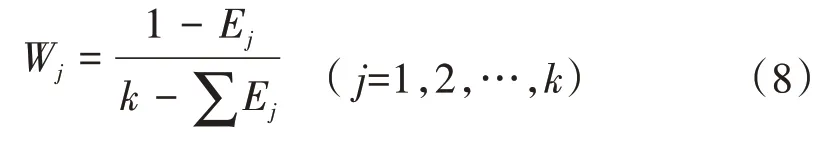
得到参数的信息熵和权重如表4。可以看出震级的信息熵比震源深度的更大，说明其变异程度更小，包含的信息量更少，对极震区烈度的影响程度比震源深度更小。

表4 参数的信息熵和权重Table 4 The information entropy and weight of parameters

4 结论与展望

收集了2013年以前多次5 级以上地震案例，首先分析震级和震源深度与极震区烈度的关系，然后以震级、震源深度作为输入参数，以极震区烈度作为输出参数，利用ELM 建立预测模型后对2013年后18个地震案例进行预测，最后分析了震级和震源深度的信息熵和权重，主要结论如下：

（1）震级和震源深度与极震区烈度分别为正相关和负相关性关系，即极震区烈度随着震级的上升而增加，随着震源深度的上升而下降。

（2）该ELM 预测模型的预测结果精度比现有广义线性模型预测方法提高约20%。

（3）震级的信息熵比震源深度的更大，其变异程度更小，包含的信息量更少，对极震区烈度的影响程度比震源深度更小。

（4）局部地区预测结果不甚理想，针对这些区域的专门预测模型是下一步努力的方向。由于极震区烈度不仅与震级和震源深度有关，更与震源机制，地震波传播介质、路径，局部场地条件等因素有关，因此基于多参数的更加精确预测模型也应给予更多重视。