基于Prophet算法的配电网线路峰值负荷预测

李 衡，朱 理，郑 洁，刘海琼

（1.国网浙江省电力有限公司杭州供电公司，杭州 310009；2.杭州沃瑞电力科技有限公司，杭州 310012）

0 引言

电力负荷预测是电力安全调度的重要依据，在保证电力系统稳定、可靠、经济运行等方面具有十分重要的意义。随着我国经济的高速发展，电力负荷预测已成为一项重要而艰巨的任务。提前一至两星期对配电网线路进行负荷峰值预测，准确预测将出现重过载的线路，能为配电网制定供电计划提供重要参考［1-3］。

目前常用的负荷预测方法可分为传统统计方法［4-5］和现代智能方法［6-10］。传统统计方法包括指数平滑法、自回归方法等。文献［2］通过K-means算法对线路负荷增长趋势进行聚类分析，筛选出未来可能负荷较重的目标线路，再基于XGBoost算法建模进行线路峰值负荷预测，其预测模型的样本特征值数据包括：气象数据、时间数据、春季负荷数据。文献［4］提出以指数平滑法为基础的组合负荷预测模型。文献［5］提出基于自回归平均移动模型与灰色理论的负荷预测模型。现代智能方法包括：BP人工神经网络［6］、LSTM（长短期记忆）［7］、随机森林［8］、XGBoost［2，9-10］等。文献［6］提出基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测方法。文献［7］提出基于CNN（卷积神经网络）和LSTM 网络的混合模型短期负荷预测方法。文献［8］将随机森林算法引入负荷预测领域，并利用灰色投影筛选出相似日样本集合训练模型。文献［9］建立LSTM 预测模型和XGBoost 预测模型，并使用误差倒数法将LSTM 与XGBoost 组合起来进行预测。

近年来，由于Prophet 算法［11-13］在时间序列数据预测方面具有很强的优势，同时能出色地适应数据的节日效应和变化趋势点，被引入电力系统负荷预测领域。文献［11］针对大量的历史电负荷数据、日期信息、气象数据，提出基于Prophet与XGBoost 的混合电力负荷预测模型。文献［12］提出一种基于Prophet加法模型和LSTM的组合模型的短期负荷预测方法。目前基于峰值负荷预测的研究有限［14-15］，文献［14］建立基于时间序列的台区配变负荷峰值预测方法，其模型由自相关和移动平均两部分构成。文献［15］构建基于双向LSTM的幅值预测模型，再利用幅值模型的预测结果展开基于XGBoost 分类器的日峰值负荷出现时段预测。但是上述方法大部分应用于输电网日负荷曲线预测或日电量预测，却很少应用于配电网线路的峰值负荷预测［16-21］，而配电网线路负荷具有变化趋势差异性大、难以量化的特点，这对预测模型的泛化性提出了更高的要求，使得负荷预测更加困难［2］。为此，本文首先分析线路负荷曲线受节假日、季节等因素影响的变化规律，再将Prophet应用于配电网线路峰值负荷预测，基于历史日峰值负荷数据对每条线路单独建模，并采用自动调参计算方法，实现基于时间序列负荷数据的配电网线路峰值负荷预测。

1 负荷曲线分析

配电网线路负荷数据受节假日、季节等因素的影响，具有自己独特的变化规律。本文对某配电网线路负荷受节假日、季节的影响情况进行分析。

图1所示为某线路2017年7月连续两个星期的电流数据，其中7 月15 日、7 月22 日为周六，该线路周末的电流日峰值约200 A，而工作日的日峰值均大于280 A，可见周末的日峰值大辐低于工作日的日峰值，该线路日负荷峰值受是否工作日影响明显。

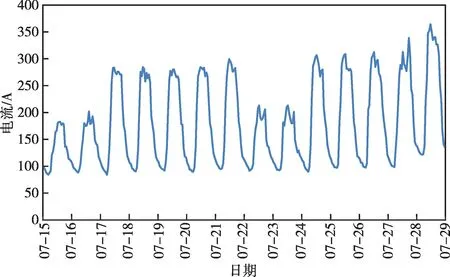
图1 某线路连续2个星期的负荷曲线

图2所示为某线路2018—2019年春节7天假期及前后各一星期的电流负荷曲线。2018-02-15、2019-02-04 为除夕，该线路除夕前一星期，负荷峰值大致呈逐渐下降趋势，初一至初五日负荷峰值明显小于春节前的日负荷峰值，从初六开始负荷逐步恢复至春节前水平。可见，受春节影响，负荷于初一至初五期间出现峰值低谷。

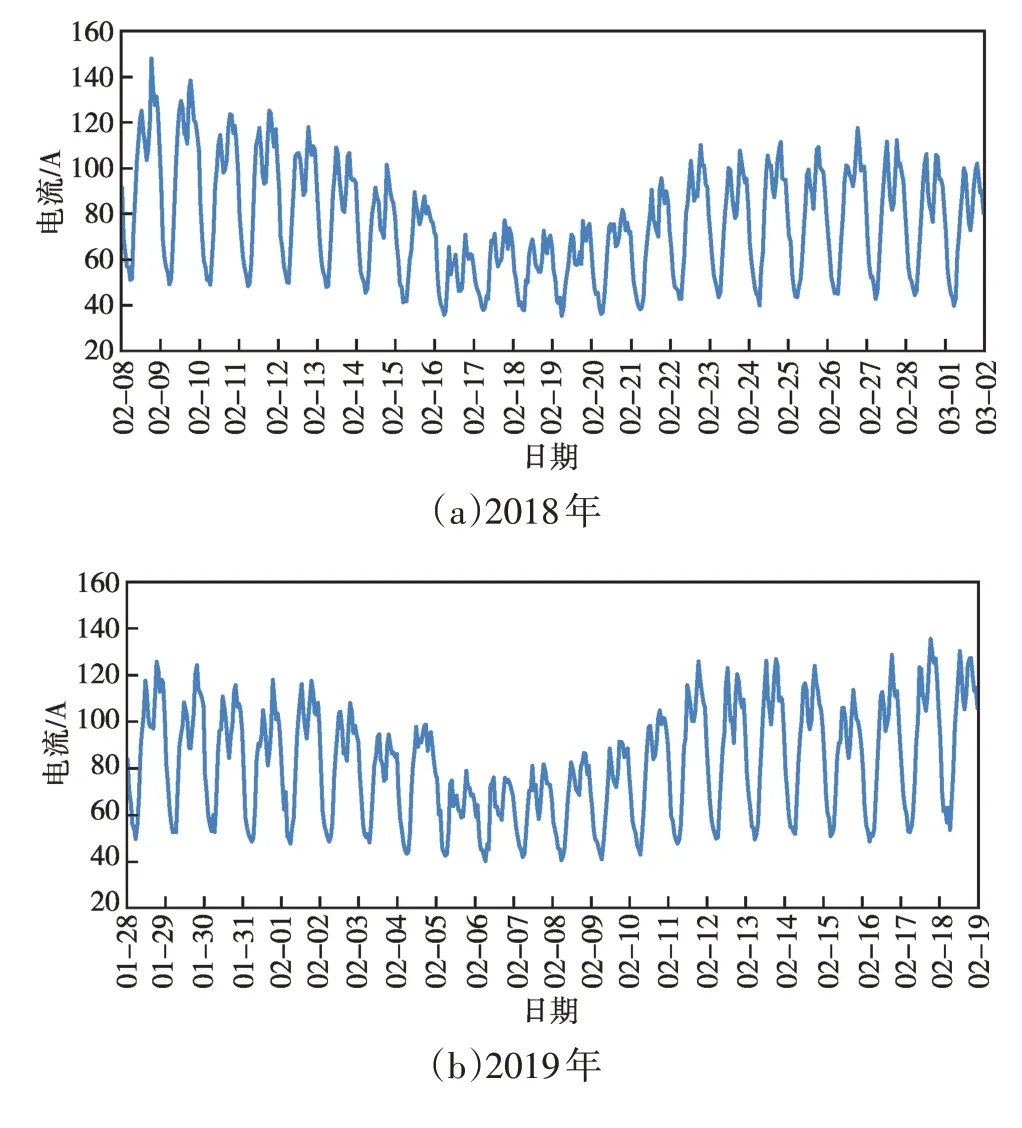
图2 某线路春节前后的负荷曲线

图3所示为某线路2018年1月负荷与7月负荷曲线，1 月日负荷峰值均值约120 A，而7 月日负荷峰值均值约为170 A。可见，受季节影响，该线路1月负荷水平明显低于7月负荷。

图3 某线路同年1月与7月的负荷曲线

综上所述，配电网线路负荷受节假日、季节影响，且具有特定的变化趋势，因此本文利用Prophet 在预测时序性数据的周期性、节假日和趋势变化方面的优势，进行峰值负荷预测。

2 Prophet预测模型

2.1 Prophet模型原理

2017 年2 月，Facebook 发布了时间序列预测框架Prophet，Prophet与传统的时间序列预测方法相比，有以下优点：有较好的灵活性，轻松适应多个季节的季节性，并通过分析对趋势做出不同的假设；测量值不必呈等间距分布，不需要插值缺失值；拟合速度较快等［11］。

Prophet 是基于自加性模型的预测时间序列数据的模型，模型整体可分解为3个主要部分：趋势项、季节项、节假日项，其组合公式为：

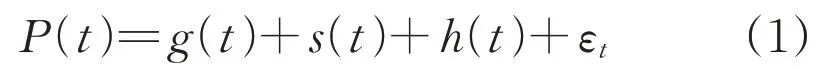
式中：g(t)为趋势项；s(t)为季节项；h(t)为节假日项；εt为误差项。通常假设εt服从均值为0的正态分布，主要用来反映未在模型中体现的异常变动。

g(t)表示时间序列的非周期变化趋势，包括饱和增长模型与分段线性增长模型，根据数据中的变化点检测趋势走向。本文采用饱和增长模型：

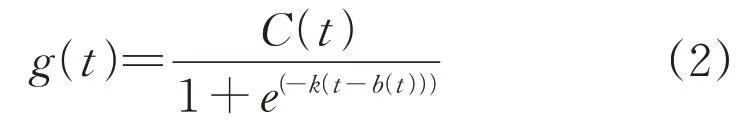
式中：k为增长率；b(t)为偏移量；C(t)为模型容量；随着t的增加，g(t)趋近于C(t)。

s(t)代表周期性变化，为了拟合并预测季节的效果，Prophet 基于傅里叶级数提出了一个灵活的模型，s(t)可根据以下公式进行估算：

式中：N为周期总数；T为某个固定的周期，年度数据的T为365.25，周数据的T为7；2n为期望在模型中使用该周期的个数；a1，a2，…，aN，b1，b2，…，bN为模型中需要估计的参数。

h(t)代表节假日效果，节假日可能导致时间序列数据出现波动。而节假日的周期不固定，不能通过周期性模型实现，因此对不同节假日建立独立模型，给每个独立模型制定一个时间窗口，同一个窗口中的影响为相同值。节假日效果模型h(t)根据以下公式进行估算：

式中：L为节假日集合；i为第i个节假日；κi为对应节假日对预测值的影响因子；Di为窗口期中包含的时间t。

定义Z(t)=[l(t∈D1)，…，l(t∈DL)])，可得：

式中：v越大，表示节假日影响力越大。

2.2 线路峰值负荷预测模型

由于每条配电网线路的负荷变化规律不同，因此本文对每条需要进行负荷峰值预测的线路提取其近几年的日负荷峰值，建立Prophet时间序列负荷模型。

本文对某市城区配电网线路2020-08-01—2020-08-21 共3 个星期的峰值进行预测，由于历史负荷数据距离预测时段的时间越远，其对预测时段负荷的影响越小，因此本文采用的历史数据负荷数据为：2017-07-01—2020-08-21 的电流数据，线路负荷采样间隔为1 h，即每天24个电流数据，提取每天的日负荷峰值。

线路Prophet时间序列负荷模型的输入数据分为日期ds和日负荷峰值y两列，如下式所示：

式中：dn为第n天的日期；yn为第n天的日负荷峰值。输出数据为未来一星期（即［dn+1，dn+2，dn+7］）的日负荷峰值。

2.3 数据预处理

配电网线路负荷数据常常存在数据不完整、异常数据等现象，而Prophet算法的优点之一是不需要补充缺失值，算法自身可以通过插值处理缺失值，但是Prophet 算法对异常值比较敏感。因此，为避免异常值影响模型预测效果，本算法将小于10 A 或大于800 A 的线路日负荷峰值置为无效值NA。

2.4 历史节假日数据

本算法设置的历史负荷数据期间的节假日窗口如表1所示，其中lower_window为节日前几天，upper_window为节日后几天。

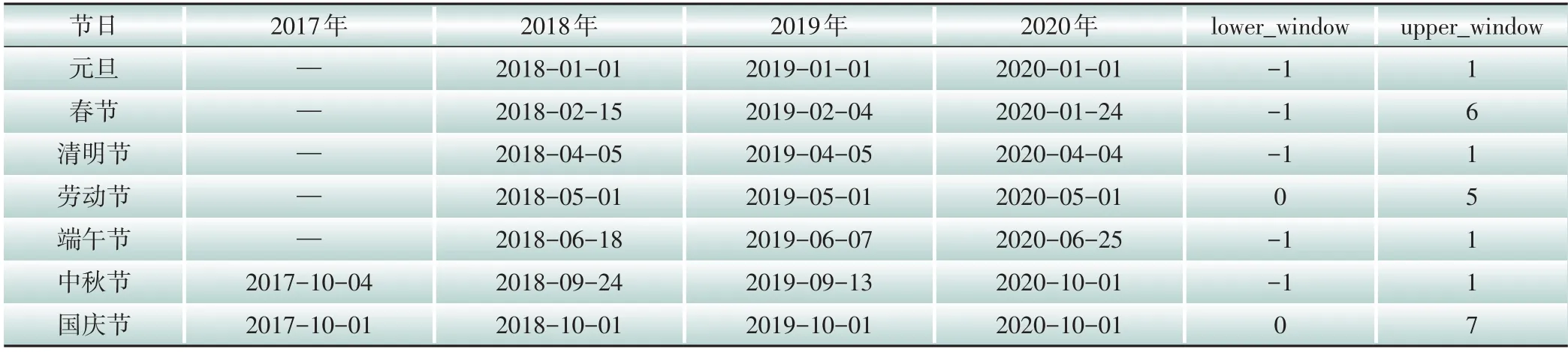
表1 节假日特征

2.5 预测指标

本文选用的预测指标为峰值负荷预测误差EPEAK：

式中：ypeak为预测时段线路实际电流峰值；为预测时段线路预测电流峰值；Icontrol为线路最大允许电流。

3 模型自适应调参

Prophet 算法中有两个重要指标：变点增长率（以下简称为“c”）与变点个数（以下简称为“p”）。

Prophet 能自动监测变点，变点个数由参数p来决定。如果数据趋势的变化被过度拟合或者拟合不足，可以利用输入c来调整稀疏先验的程度。c默认值为0.05，其值增大会导致趋势拟合得更加灵活，其值减小会导致趋势拟合的灵活性降低。每条线路的峰值变化趋势不一样，c值与p值的选取将直接影响预测的结果。

因此，本文提出自适应计算方法，通过对每条线路上一周期进行峰值负荷预测来计算出该线路当前预测时段的最优c值与p值，具体流程如图4所示。对于每条线路：

图4 自适应调参流程

1）设置初始参数值c与p。

2）基于上一周期，即用ds=[d1，d2，…，dn-8]预测[dn-7，dn-6，…，dn-1]的日负荷峰值，由于上一周期实际负荷已知，因此可计算预测峰值误差。

3）判断上一周期预测峰值误差是否大于误差门槛值，若预测峰值误差大于门槛值，执行下一步4），否则跳转到5）。

4）按设定调整步长改变c或p，并判断c与p是否在允许范围内，若是则继续进行2），否则进入5）。

5）退出参数计算，提取上一周期预测误差最小时对应的c做为cbest，p做为pbest。

6）用cbest与pbest进行本周期的峰值负荷预测，即预测[dn+1，dn+2，...dn+7]的日负荷峰值。

以预测周期2020-08-01—08-07 为例，其上一周期为2020-07-25—07-31。

4 算例分析

本文对某城区配电网175 条10 kV 线路2020-08-01—08-21 日共3 个星期的峰值进行预测，所用实验平台条件为Windows10 X64 操作系统、In-ter i5-8265 CPU，使用Python 语言编程实现。Prophet 模型参数中c值和p值采用自适应计算方法，其它参数统一固定设置，其中：seasonality_mode 为“additive”，seasonality_prior_scale 为20，interval_width为0.8，changepoint_range为0.9。

4.1 自适应调参结果分析

Prophet模型参数中的c值和p值采用自适应计算方法，c值初始值为0.05，增长步长为0.02，最大为0.23。p值初始值为20，增长步长为5，最大为50。

本文通过固定p值，分析c值对峰值误差EPEAK的影响。在某周期预测计算结果中，4条典型线路c值与EPEAK的变化关系如图5 所示。由图5 可见，随着c值的逐渐增加，EPEAK值有以下几种变化趋势：

图5 典型线路c值与峰值误差EPEAK变化关系

1）线路1、线路2的预测误差逐渐减小，两条线路的预测误差均下降了0.04。

2）线路3在c值从0.07增加到0.09时，EPEAK由0.15降至0.14，而c由0.09增加至0.23，EPEAK均保持为0.14。

3）线路4在c值从0.07增加到0.13时，EPEAK由0.14增加至0.16，而c由0.15增加至0.23，EPEAK均保持为0.17。

可见，c值的选取，直接影响着线路的峰值预测误差大小。线路1、线路2的cbest为0.23，线路3的cbest为0.09，线路4的cbest为0.15。

4.2 单条线路预测结果分析

本文以2条变化趋势差异较大的线路为例来分析，线路1的Prophet模型可视化展示如图6所示，线路2的Prophet模型拟合效果如图7所示。

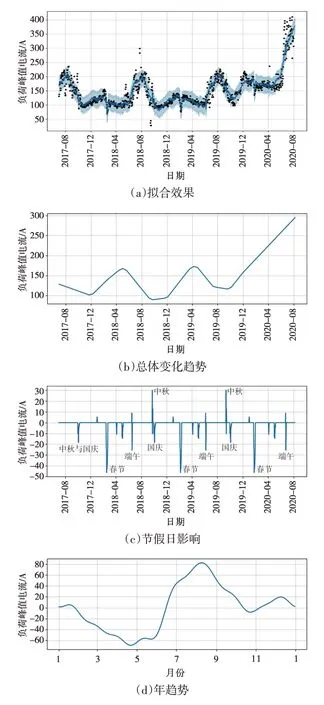
图6 线路1负荷模型可视化展示

图7 线路2负荷模型可视化展示

图6（a）为线路1 的历史日负荷峰值数据与模型拟合效果，图中小圆点为实际历史日负荷峰值，曲线为模型拟合后的日负荷峰值变化曲线。可见算法拟合效果较好，与原始负荷数据基本贴合。历史负荷曲线表明，2020 年之前负荷变化年周期性明显，夏高冬低，但2020年负荷出现大辐增长，推测原因是受2020年极端天气导致空调负荷增加、全球新冠疫情使工厂订单突增等影响。

图6（b）为线路1 的总体趋势，可见该线路2017年7月与2019年12月负荷变化趋势接近，但2020年负荷比同期出现明显大幅增长趋势。

图6（c）为线路1的节假日影响，可见：

1）春节对该线路负荷影响最大，负荷在春节期间出现下降趋势。

2）2017年中秋节在国庆节内，负荷出现下降。2018—2019 年中秋节在国庆假期前，中秋节负荷升高，国庆节负荷下降。

3）端午节、劳动节、清明节线路负荷下降。

4）元旦节线路负荷略有上升。

图6（d）为线路1 的年趋势，可见该线路7—9月为全年负荷的高峰期，其中8 月为负荷最高峰时期。

图7 为线路2 的历史峰值数据与模型拟合效果，与图6（a）对比可见，线路1与线路2的变化趋势差异很大，但Prophet模型均能很好地拟合。

4.3 所有线路预测误差分析

对175条线路进行3个星期的负荷预测，统计结果如表2 所示。可见，08-01—08-07，EPEAK在［0，0.05］区间占70.86%，EPEAK在［0，0.1］区间占91.43%，EPEAK在［0，0.15］区间占97.71%，08-08—08-14 与08-15—08-21 的EPEAK在［0，0.05］区间的占比略有增加，但EPEAK在［0，0.1］与［0，0.15］区间的占比略有降低。但3 个星期平均占比中，EPEAK在［0，0.05］区间占73.14%，EPEAK在［0，0.1］区间占89.52%，EPEAK在［0，0.15］区间占94.86%。可见，该算法预测准确度基本满足工程实际需求。

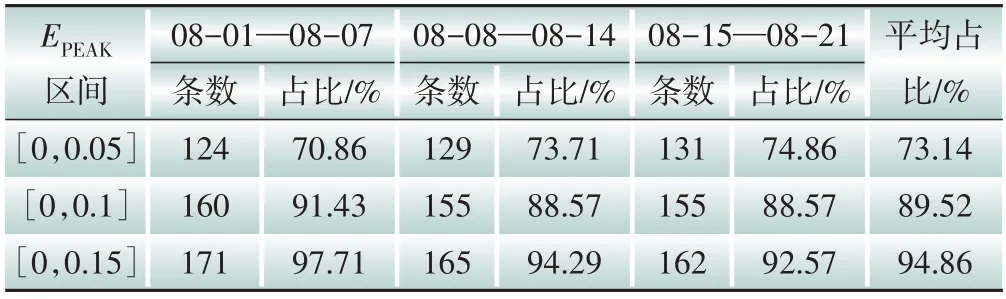
表2 峰值负荷预测误差统计

为对比预测效果，采用文献［2］所述XGBoost峰值负荷预测方法结合气象特征数据、时间特征数据、春季负荷特征数据进行08-01—08-21的峰值负荷预测，所有气象数据均采用实际气象数据，统计XGBoost 算法平均预测误差，并与本文所提出的Prophet算法进行比较，结果如表3所示。

表3 2种算法预测结果对比

由表3 可见2 种算法的峰值预测误差在EPEAK在［0，0.05］、［0，0.1］、［0，0.15］3 个区间的占比，其中XGBoost 算法的误差均略高于Prophet 算法；两种算法的预测误差在EPEAK在［0，0.1］、［0，0.15］区间内占比仅相差约1%。相比而言，XGBoost算法预测平均误差更小，但XGBoost 算法除了需要负荷数据外，还需获取相关气象数据，且预测未来时段的负荷峰值时，预测准确度依赖于天气预测的准确度。而Prophet算法仅依赖于时间序列的负荷数据即可达到接近XGBoost算法的计算结果。因此，Prophet 算法更易于推广至工程实际应用中，预测准确度也基本满足工程实际需求。

5 结论

本文提出一种基于Prophet算法的配电网线路峰值负荷预测算法，得出以下结论：

1）配电网线路负荷数据受节假日、季节等因素的影响，具有自己独特的变化规律。

2）采用Prophet预测算法针对每条线路单独建模，且仅以日负荷峰值数据为输入数据，对每条线路自适应选取c和p参数，并通过实际算例证明该算法的预测准确度能满足工程实际需求。

3）Prophet 预测方法支持多角度可视化，能直观了解线路负荷历史变化趋势、受节假日影响程度；且无需补齐丢失的数据。

4）对配电网线路历史负荷数据的完整率要求低。

该预测方法可准确实现配电网线路峰值负荷预测，易于推广至工程实际应用中，其不足之处在于未考虑气象数据等影响因素，对于气温敏感型负荷的预测效果可能欠佳，下一步可与基于多个影响因素的深度学习算法进行结合预测。