中国区域3种数值模式的地面气象要素预报初步评估
岳艳霞 任芝花 刘娜 石岩
1 石家庄市气象局,石家庄 050081 2 国家气象信息中心,北京 100081
1 引言
世界上主要数值天气预报中心都拥有各自的全球中期预报模式,欧洲模式预报的准确性、精细化始终是各国模式发展的主要目标(管成功等, 2008)。
GRAPES(Global/Regional Assimilation and Prediction System)模式是我国自主研发的新一代数值预报模式,它兼顾全球与有限区两种性质不同的预报区域,填补了我国数值预报领域的数项技术空白 (张人禾和沈学顺, 2008; 陈超君等, 2012)。另外它基于多尺度通用模式,能够针对不同的区域和物理过程选择不同的运行模块,在提高模式精度并有利于后续研发的同时有效降低业务运行成本(闫之辉等, 2010; 张萌等, 2018)。GRAPES模式的区域版本GRAPES_MESO自2004年5月9日开始业务试运行(毛冬艳等, 2014),经过十几年不断改进完善,2018年已发展到V4.3版本。GRAPES模式的全球版本GRAPES_GFS于2009年实现准业务化,之后经过模式物理过程的完善、三维变分同化系统的改进、卫星资料同化应用的增加和模式协同的调整,于2016年建立了GRAPES_GFS2.0的预报模式(张萌等, 2018)。
数值预报理论的不断发展完善,加上高速度、大容量的巨型计算机及网络的快速发展,使得数值预报成为天气预报的基础和重要手段。然而,大气是极其复杂的系统,受多种因素影响,天气系统的演变是非线性、不确定性和时变的过程。因此对数值预报产品进行检验不仅可以为模式改进提供建议 (董全等, 2016),也可以让气象服务人员更好地了解各种数值模式产品的性能,在提供数值预报产品的服务中更具针对性。许多学者对中国区域多种模式多种要素进行了不同时间段的检验评估,龚伟伟等 (龚伟伟等, 2015a)用ECMWF(欧洲中期数值预报中心)和JMA(日本气象厅)及GFS(美国国家海洋大气局的全球预测系统)3种模式对中国区域气温、湿度、风速等要素进行了评估,指出ECMWF模式优于其他模式,东部预报效果好于西部。龚伟伟等(龚伟伟等, 2015b)还用JMA、ECMWF两种数值模式对中国区域平均海平面气压和地面风速等要素进行了评估,指出两种模式东部适用性优于西部,JMA、ECMWF在不同区域各具优势。赵天保等(赵天保和符淙斌, 2009; 赵天保和华丽娟, 2009)对几种再分析地表气温、地表气压资料在中国区域的适用性进行了评估,指出再分析产品与观测资料的差异具有明显的区域和季节变化特征。上述检验评估多采用误差、标准差、相关等指标,使用的站点多为国家气象站。近年来关于GRAPES_MESO和GRAPES_GFS预报与实况检验的研究不断增多,但关于两种预数值报之间的对比及两种数值预报与ECMWF等其他数值模式的对比检验还不多见。陈超君等(陈超君等, 2012)对温哥华冬奥会场馆GRAPES_MESO 湿度、气温、风、降水预报与实况进行了对比分析,指出气温预报偏低,风速预报偏大,湿度预报准确率最高,0.1 mm降水评分最高且存在系统误差等;张萌等(2018)对比分析了GRAPES_GFS2.0 与 NCEP FNL的差异,指出误差大值集中在中高纬度地区,且冬季最大,夏季最小;毛冬艳等(毛冬艳等, 2014)对GRAPES_MESOv3.3模式强天气预报性能进行了初步检验,指出模式降水空报改进明显,对强降水有一定预报能力,但预报性能不够稳定,对台风降水强度预报较好,但落区具有一定误差。
气象预报应用于社会各行各业,对国民经济和社会发展的作用越来越受到重视。ECMWF和GRAPES预报产品是国内目前主要的应用服务产品。为了了解ECMWF和GRAPES预报产品的性能,使用户在实际应用中,根据需求可选择性地应用上述预报产品,本文分别利用中国气象局2421个国家级自动站和8155个地面天气站(骨干站)逐时观测资料对ECMWF和GRAPES_MESOv4.3、GRAPES_GFSv 2.0的气温、地表温度、湿度、风速、降水在中国区域的适用性进行了对比研究。
2 资料及处理
2.1 资料说明
本文所用的数值模式资料为2017年7月(简称7月)和11月(简称11月)、2018年1月(简称1月)和4月(简称4月)ECMWF确定性预报模式(简称C1D)的0~72 h气温、地表温度、露点温度、风速、小时累积降水预报资料以及GRAPES_MESO v4.3 (简称Meso)和GRAPES_GFS v2.0(简称Gfs)的0~72 h气温、地表温度、相对湿度、风速、小时累积降水预报资料。这3种数值模式资料的详细介绍见表1。4月、7月、11月、1月的统计结果分别代表春、夏、秋、冬4个季节的特征。

表1 数值模式资料说明Table 1 Information of numerical model data
本文分别利用中国气象局国家级自动站和地面天气站观测资料与模式预报进行了对比研究,发现在站点较多且数据较完整的东部地区评估结果与站点类型选取关系不大。王雨等(王雨和闫之辉, 2007)也曾进行了降水检验方案变化对降水检验评估效果的影响分析,指出不同站点不同分区大雨以下各级降水评估结果差别不大。本文分析中使用的站点为国家站和地面天气站,增大西部站点数量。站点分布和站点海拔高度及分区(赵天保和华丽娟, 2009)见图1a(其中,北方半干旱区简称为北半干)。因为地面天气站为区域自动站,观测要素种类不同,所以分析中不同要素参与统计的台站数量不同(图1b)。台站观测资料取自于国家气象信息中心的CIMISS系统。
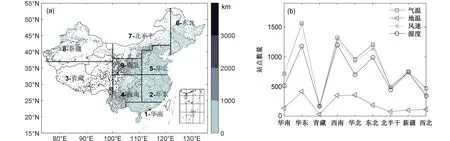
图1 (a)本文使用的站点分布与站点海拔高度及中国9个分区;(b)中国9个分区气温、地表温度、风速、湿度的站点数量Fig. 1 (a) Distribution of observation stations with altitudes presented in this article and the nine subregions over China; (b) station numbers of different elements and the nine subregions over China
2.2 资料处理
因为所获取的ECMWF资料没有地面相对湿度信息,所以本文通过露点温度和气温计算出相对湿度(盛裴轩等, 2005)。
本文采用双线性插值法将数值模式格点资料插值到观测站点,将模式与观测同一时刻数据形成的匹配样本数据进行分析。对气温在插值过程中由于地形差异引起的误差进行了地形订正(赵天保和符淙斌, 2009a)。
2.3 评估方法
本文主要采用误差E与平均误差ME、均方根误差RMSE、预报准确率、相关系数r等参数评估各数值预报模式的预报性能。
(1)误差E与平均误差ME
Ei为预报与实况的误差值:Ei=Fi-Oi,Fi为预报值,Oi为观测值。
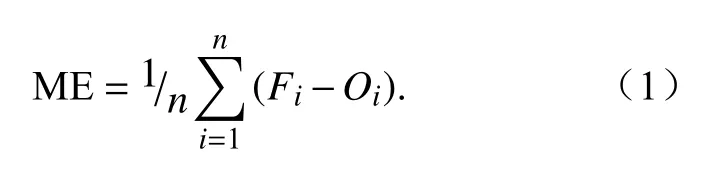
分析中同时计算了误差的概率分布情况及平均误差统计值,综合分析二者可以看出模式预报是否存在系统误差。
(2)均方根误差RMSE
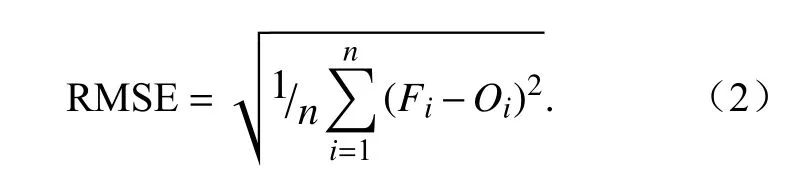
预报与观测实况的均方根误差表示模式预报与观测实况的误差大小。
(3)预报准确率为模式预报正确的站次数与模式预报总站次数之比。参照中国气象局《天气分析预报质量检验方法》中的规定(陈超君等, 2012):气温: |Fi-Oi|≤2 K;地表温度: |Fi-Oi|≤5 K;相对湿度: |Fi-Oi|≤10%; 风速: |Fi-Oi|≤2m/s。若要素满足上述各检验公式,则认为模式预报准确。预报准确率可以反映一个模式对不同气象要素的预报性能优劣。
(4)相关系数r
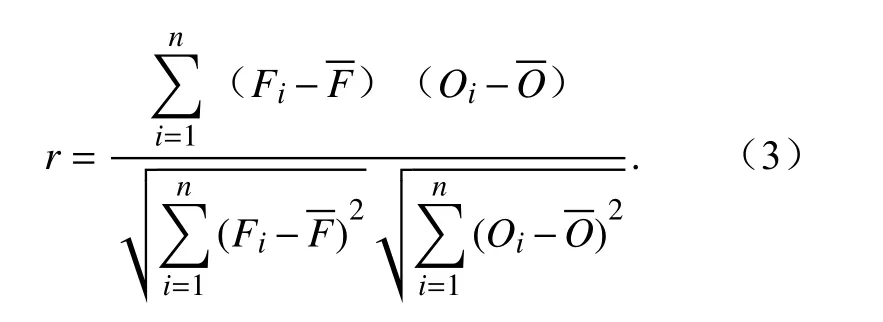
模式预报与观测实况的相关系数可检验模式对观测实况日变化、逐日变化的模拟预报能力,相关系数越大模拟能力越强。
3 结果与分析
因为不同要素、不同季节对比分析的站点数量不同,所以样本数量也不同。去除缺测数据,样本数量最多的是7月的气温,样本量超过1000×104,样本数量最少的是1月的地表温度,样本量约为160×104。
3.1 气温
3.1.1 评估参数均值特征
表2给出数值模式与观测气温的平均误差、均方根误差、预报准确率和相关系数在不同月份和年的统计值。结合误差概率分布(图略)和各评估参数的统计值可以发现:气温误差主要集中在[-5 K,5 K],此区间样本数量Meso和Gfs占全部样本的90%,C1D超过95%。平均误差4月和7月Meso为正值,Gfs为负值,C1D接近0值。11月Gfs平均误差为负值,Meso和C1D为正值,1月3个模式的平均误差均为正值。说明春、夏季气温Meso预报易高估,Gfs预报易低估,冬季3个模式预报均易高估。均方根误差Meso和Gfs大于3 K,C1D在2.5 K左右,预报准确率Meso和Gfs低于65%,C1D高于73%,相关系数Meso和Gfs大于0.8,C1D大于0.9。3个模式总体表现出4月、1月相比7月、11月均方根误差略高,预报准确率略低,相关系数略小,说明3个模式气温预报能力夏秋季优于冬春季。另外从各评估参数的数值可以看出C1D气温预报能力最好,Gfs略好于Meso。
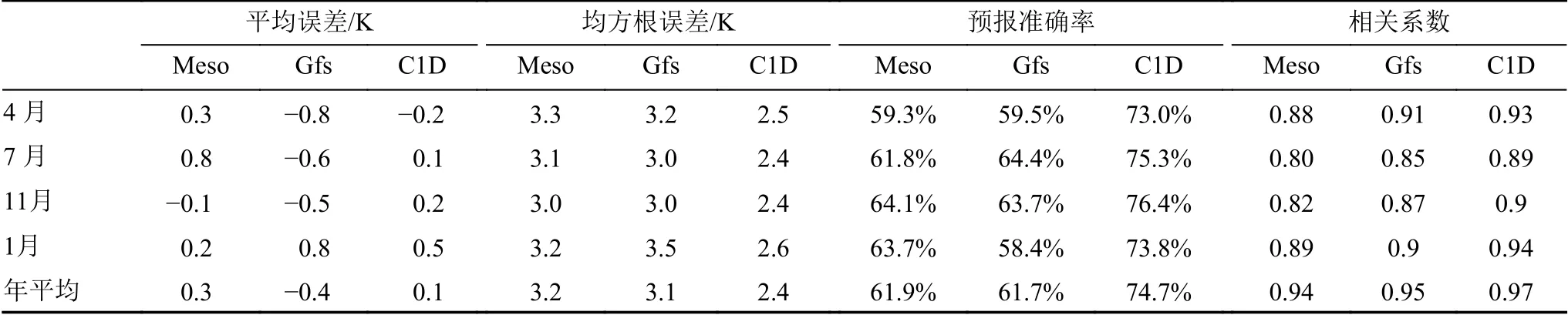
表2 数值模式模拟与观测气温资料各评估参数统计值T able 2 Statistics of evaluation parameters of the air temperature between the numerical model predictions and observations
3.1.2 评估参数空间分布特征
图2给出数值模式资料和观测气温的平均误差、均方根误差、预报准确率和相关系数年均值的空间分布特征。图3给出不同评估参数在不同月份、不同区域的平均值分布特征。综合图2和图3可以看出:3个模式在青藏地区均为负误差,新疆地区4月为负误差,1月为正误差。C1D除4月外,其他月份全国大部分地区为正误差,误差值较小。Gfs除1月外,其他月份全国大部分地区均为负误差,特别是东北地区,负误差值较大。Meso在4月、7月全国大部分地区为正误差,11月、1月区域分布特征没有明显规律。还可以看出Gfs和Meso不同区域间误差值差异较大。3个模式青藏和新疆地区的均方根误差明显高于其他地区,青藏地区3种模式均方根误差相差不大,在4 K左右;新疆地区Meso、Gfs、C1D均方根误差分别为4.1 K、4.3 K、3.1 K;其他地区C1D均方根误差在2~2.5 K,Gfs和Meso均方根误差相当,在2.5~3.5 K。3个模式青藏和新疆地区的预报准确率明显低于其他地区,青藏地区3种模式预报准确率相差不大,在50%左右;新疆地区Meso、Gfs、C1D预报准确率分别为38%、33%、58%;其他地区C1D预报准确率在70%~90%,Gfs和Meso预报准确率接近,在50%~70%。除7月外,3个模式青藏地区相关系数明显低于其他地区,新疆地区相关系数与其他地区相似,大于0.8。Meso 7月南部地区相关系数较低,11月北部地区相关系数较低,在0.75左右。3个模式所有评估指标均有明显的区域分布特征,多表现为从东南向西北预报能力越来越差,青藏、新疆地区的预报能力最差。
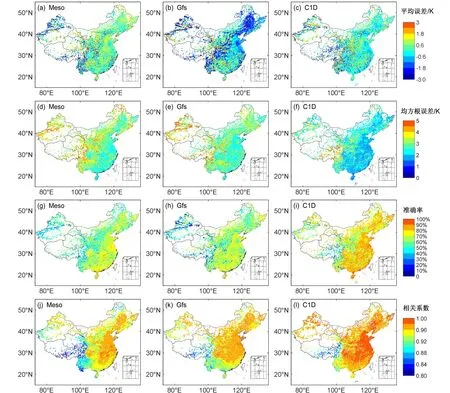
图2 Meso(第一列)、Gfs(第二列)、C1D(第三列)数值模式模拟与观测气温评估参数的空间分布:(a、b、c)平均误差;(d、e、f)均方根误差;(g、h、i)预报准确率;(j、k、l)相关系数Fig. 2 Spatial distribution of evaluation parameters of the air temperature between the numerical model predictions using Meso (the first column), Gfs(the second column), and C1D (the third column) and observations: (a, b, c) ME (Mean Erro); (b, e, f) RMSE ( Root-Mean-Square Error); (g, h, i) the forecast accuracy of models; (j, k, l) correlation coeffcient
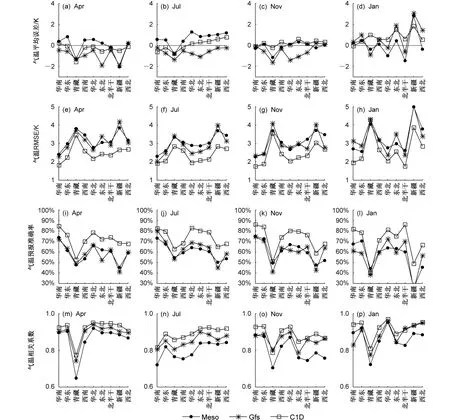
图3 Meso、Gfs、C1D数值模式模拟与观测气温在4月(第一列)、6月(第二列)、11月(第三列)、1月(第四列)中国9个分区上各评估参数统计值:(a-d)平均误差;(e-h)均方根误差;(i-l)预报准确率;(m-p)相关系数Fig. 3 Evaluation parameters of the air temperature between the numerical model predictions (Meso, Gfs, and C1D) and observations in the nine subregions over China in April (first column), July (second column), November (third column), and January (fourth column): (a-d) ME; (e-h) RMSE;(i-l) the forecast accuracy of models; (m-p) correlation coeffcient
3.1.3 均方根误差日变化特征
图4给出数值模式资料与观测气温资料不同时刻均方根误差的统计特征,进一步说明3个模式预报与气温观测资料的差异。可以看出,3个模式均存在随预报时效增长,均方根误差增大的特征,Meso该特征表现最显著,说明3个模式均表现随预报时效增长,预报能力下降,Meso该特征表现最明显。7月、1月北京时间白天气温较高时C1D的均方根误差值较高,夜间气温较低时C1D的均方根误差值较低,Gfs仅在7月,Meso仅在1月具有该特征,其他月份均方根误差没有明显的昼夜差异。
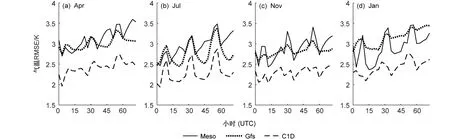
图4 Meso、Gfs、C1D数值模式模拟与观测气温均方根误差日变化特征:(a)4月;(b)7月;(c)11月;(d)1月Fig. 4 Diurnal variations of RMSE between the numerical model predictions (Meso, Gfs, and C1D) and observations of air temperature: (a) April; (b)July; (c) November; (d) January
3.2 地表温度
3.2.1 评估参数均值特征
表3给出数值模式与地表温度观测值的平均误差、均方根误差、预报准确率和相关系数在不同月份和年统计值。综合误差概率分布情况和各评估参数的统计值可以发现:地表温度误差主要集中在[-20 K, 5 K],此区间样本数量Meso与Gfs占全部样本的90%,C1D超过95%。3个模式平均误差均为负值,7月负误差最大,1月最小。说明3个模式地表温度预报均易低估,夏季低估最明显。3个模式中Gfs地表温度的预报准确率最低,与观测资料的均方根误差最大,相关系数最小。Meso与C1D的各评估参数接近,但略低于C1D。说明地表温度C1D和Meso的预报能力好于Gfs。3个模式均表现为4月、7月较11月、1月均方根误差略高,预报准确率略低,但相关系数只有C1D具有该特征。说明3个模式地表温度预报能力秋冬季优于春夏季。
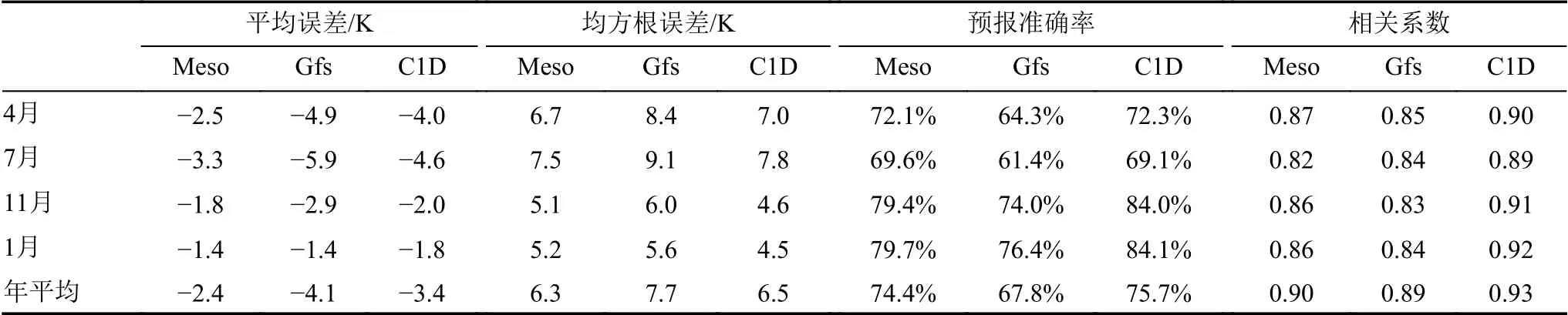
表3 数值模式模拟与观测地表温度资料各评估参数统计值Table 3 Statistics of evaluation parameters of the ground temperature between the numerical models and observations
3.2.2 评估参数空间分布特征
图5给出数值模式资料和地表温度观测值的平均误差、均方根误差、预报准确率和相关系数年均值的空间分布特征。图6给出不同评估参数在不同月份、不同区域的平均值分布特征。
综合图5和图6可以看出,除7月外,3个模式在青藏地区平均误差低于-10 K,Gfs低于-15 K。1月北半干地区Meso和Gfs平均误差明显低于C1D,约为-8 K。除1月新疆地区Gfs平均误差为正值外,其他时段全区域3个模式均为负值。4月、7月全国区域内Meso平均误差均低于C1D。说明3个模式地表温度预报存在系统误差,除1月新疆地区Gfs易高估外,其他时段3个模式在全国区域均易低估,Gfs低估值最大,4月、7月Meso低估值最小。除7月外,3个模式青藏地区的均方根误差明显偏高,在15 K左右,预报准确率明显偏低,在20%左右。1月Meso、Gfs在北半干和新疆地区的均方根误差明显高于其他地区,在10 K左右,预报准确率明显偏低,在30%左右。3个模式华南、华东、西南、华北、东北等地区均方根误差11月、1月在4~6 K,预报准确率在70%~90%,4月、7月均方根误差在5~10 K,预报准确率在50%~80%,存在明显的季节差异,预报能力春夏季低于秋冬季。除7月外,3个模式在青藏地区相关系数均明显低于其他地区,其他时间地区差异不明显。C1D相关系数最高,Gfs和Meso不同区域不同月份各有高低。和气温相似,3个模式所有评估指标均有明显的区域分布特征,多表现为从东南向西北预报能力越来越差,青藏地区的预报能力最差,但新疆地区与其他地区预报能力差异不明显。
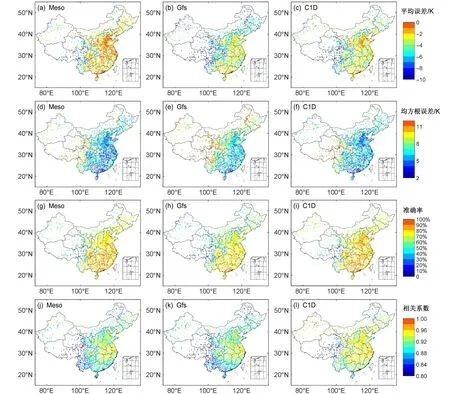
图5 Meso(第一列)、Gfs(第二列)、C1D(第三列)数值模式模拟与观测地表温度评估参数的空间分布:(a、b、c)平均误差;(d、e、f)均方根误差;(g、h、i)预报准确率;(j、k、l)相关系数Fig. 5 Spatial distribution of evaluation parameters of the ground temperature between the numerical model predictions using Meso (the first column), Gfs (the second column), and C1D (the third column) and observations: (a, b, c) ME; (b, e, f) RMSE; (g, h, i) the forecast accuracy of models;(j, k, l) correlation coeffcient
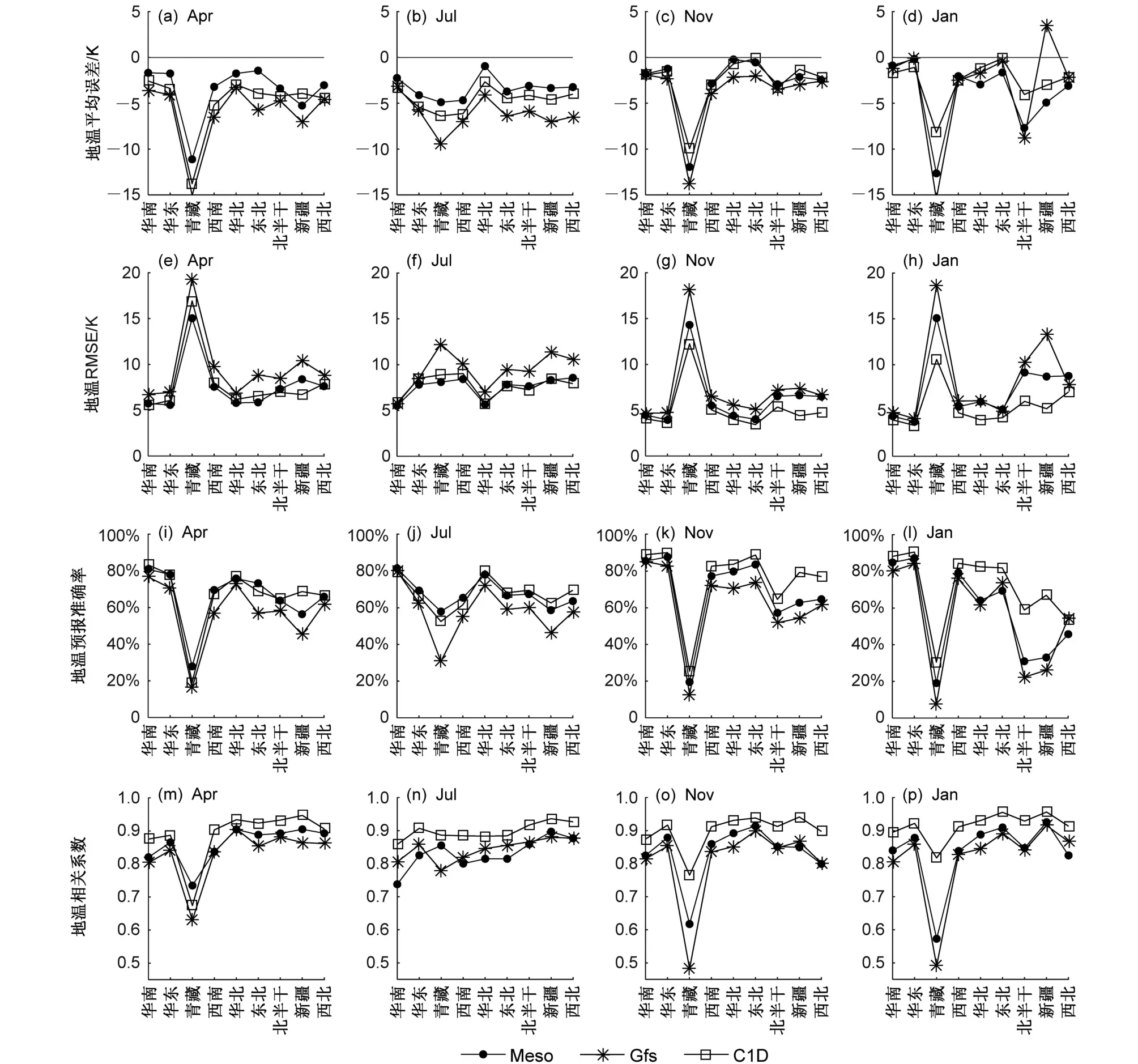
图6 Meso、Gfs、C1D数值模式模拟与观测地表温度在4月(第一列)、6月(第二列)11月(第三列)、1月(第四列)中国9个分区上各评估参数统计值:(a-d)平均误差;(e-h)均方根误差;(i-l)预报准确率;(m-p)相关系数Fig. 6 Evaluation parameters of the ground temperature between the numerical model predictions (Meso, Gfs, and C1D) and observations in the nine subregions over China in April (first column), July (second column), November (third column), and January (fourth column): (a-d) ME; (e-h) RMSE;(i-l) the forecast accuracy of models; (m-p) correlation coeffcient
3.2.3 均方根误差日变化特征
图7给出不同时刻均方根误差的统计特征。可以看出,3个模式特征相似,北京时间白天气温较高时均方根误差值较高,夜间气温较低时均方根误差值较低,存在明显的昼夜差异。夜间不同季节均方根误差最低值在2~4 K,白天均方根误差最高值季节差异较大,4、7月在12~15 K,11月、1月在7~10 K,同样表现出春夏季高于秋冬季的特征。可见,前面提到的华南、华东、西南、华北、东北等地区预报能力春夏季高于秋冬季主要体现在白天最高地表温度的预报。
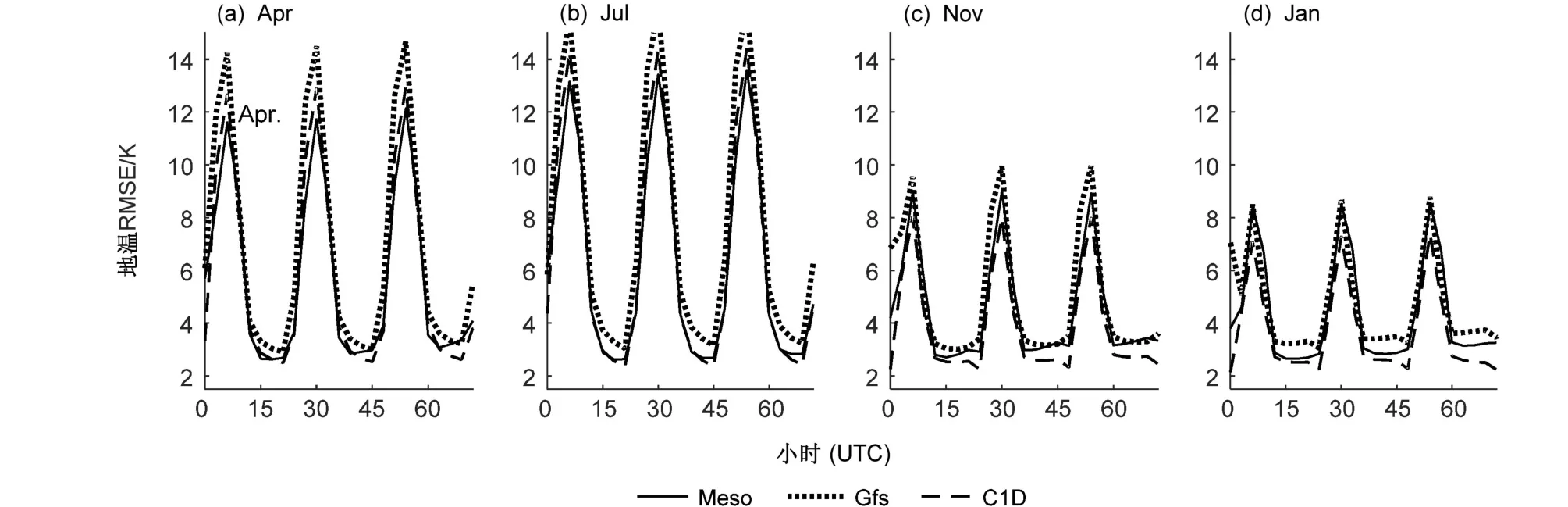
图7 Meso、Gfs、C1D数值模式模拟与观测地表温度均方根误差日变化特征:(a)4月;(b)7月;(c)11月;(d)1月Fig. 7 Diurnal variations of RMSE between the numerical model predictions (Meso, Gfs, and C1D) and observations of the ground temperature: (a)April; (b) July; (c) November; (d) January
3.3 风速
3.3.1 评估参数均值特征
表4给出数值模式与风速观测值的平均偏差、均方根误差、预报准确率和相关系数在不同月份和年统计值。综合误差概率分布情况和各评估参数的统计值可以发现:风速误差主要集中在[-2 m/s,5 m/s],此区间样本数量C1D与Gfs占全部样本的95%,Meso为85%。3个模式风速平均误差均为正值,Meso平均偏差值最大,说明模式预报易高估,Meso高估最明显。均方根误差Meso最大,在2.7~3.1 m/s,Gfs次之,在2.2 m/s左右,C1D最小,在1.9 m/s左右。预报准确率C1D最高,大于85%,Gfs次之,在75%左右,Meso最低,小于70%。3个模式均表现为4月均方根误差最大,预报准确率最低,说明3个模式风速预报能力春季最差。相关系数同样表现为C1D最高,Meso最低,Gfs居中。3个模式相关系数值明显低于其他观测要素。从各评估参数的数值可以看出C1D风速预报能力最好,Gfs次之,Meso最差。
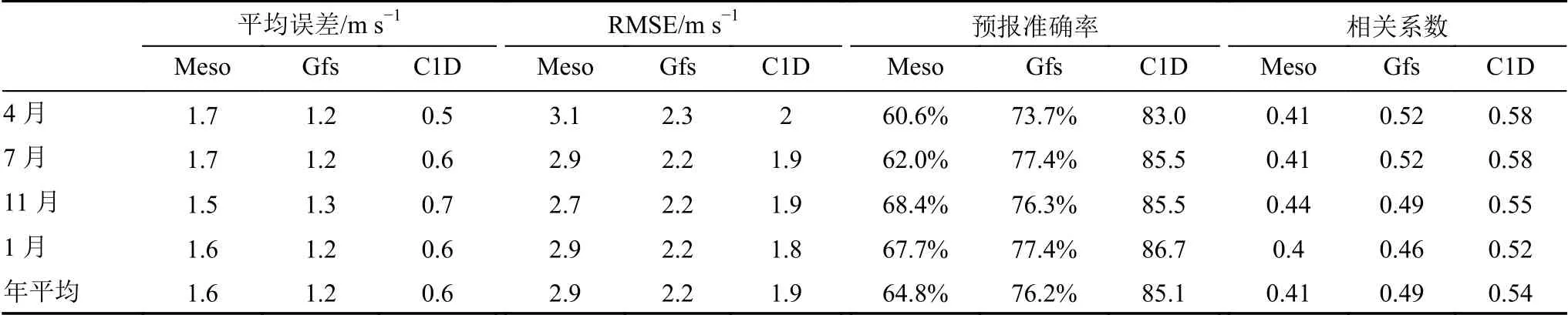
表4 数值模式模拟与观测风速资料各评估参数统计值Table 4 Statistics of evaluation parameters of the wind speed between the numerical model predictions and observations
3.3.2 评估参数空间分布特征
图8给出数值模式资料和风速观测值的平均偏差、均方根误差、预报准确率和相关系数年均值的空间分布特征。图9给出不同评估参数在不同月份、不同区域的平均值分布特征。
综合图8和图9可以看出:青藏地区C1D全年平均误差为负值,Gfs和Meso为正值。说明除C1D青藏地区风速预报易低估外,3个模式风速预报易高估。华北及以南地区3个模式误差值差异明显,Meso误差值最大,华北以北地区Meso与Gfs误差值相近,略高于C1D。C1D均方根误差不同区域间差异较小,华北及以南地区Meso均方根误差明显高于C1D和Gfs,在3 m/s左右,Gfs在2 m/s左右,C1D在1.5~2 m/s;华北以北地区4月、7月Meso均方根误差仍高于Gfs和C1D,11月、1月Meso均方根误差与Gfs接近,略高于C1D;华北以北地区Meso均方根误差存在明显的季节差异,春夏季高,秋冬季低。东北地区3个模式均方根误差值差异最小。3个模式的均方根误差特征在预报准确率有相同的表现。华北及以南地区Meso预报准确率明显低于C1D和Gfs,在60%左右,Gfs在80%左右,C1D高于80%,华东和西南地区C1D预报准确率达到90%;华北以北地区Meso与Gfs接近,在70%左右,C1D高于80%,华北、东北C1D1月预报准确率达到90%。相关系数3个模式分布特征相似,华北、东北、北半干地区最高,大于0.6。华东、华南次之,在0.5~0.6。西南、新疆、西藏最低,在0.2~0.4。以上描述说明华北及以南地区Meso预报能力明显低于GFS和C1D,华北以北地区Meso预报能力优于华北及以南地区。所有评估指标均有明显的区域分布特征,3个模式华北及以南地区空间分布特征差异大,华北以北地区相似度较高。
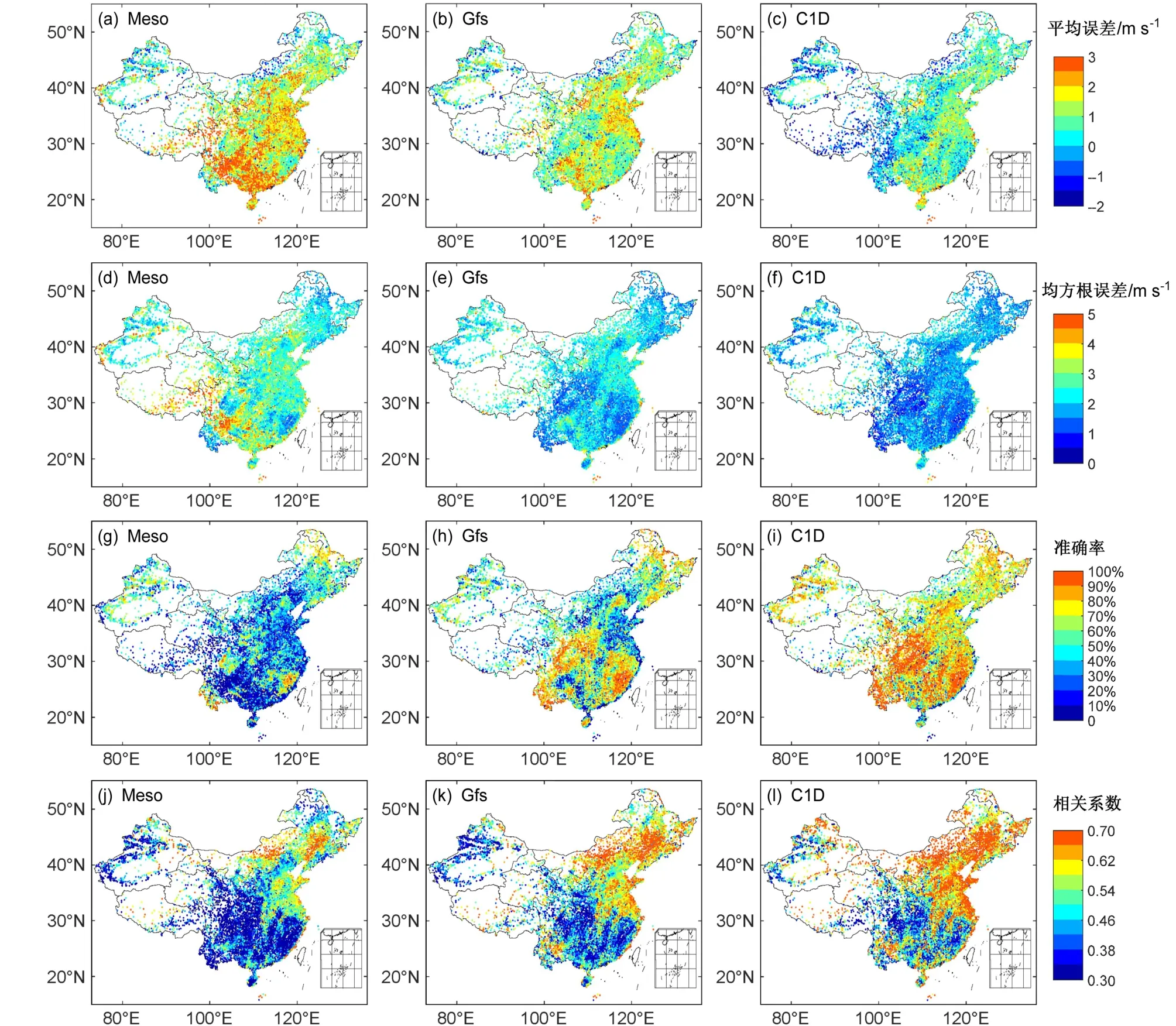
图8 Meso(第一列)、Gfs(第二列)、C1D(第三列)数值模式模拟与观测风速评估参数的空间分布:(a、b、c)平均误差;(d、e、f)均方根误差;(g、h、i)预报准确率;(j、k、l)相关系数Fig. 8 Spatial distribution of evaluation parameters of the wind speed between the numerical model predictions using Meso (the first column), Gfs(the second column), and C1D (the third column) and observations: (a, b, c) ME; (b, e, f) RMSE; (g, h, i) the forecast accuracy of models; (j, k, l)correlation coeffcient
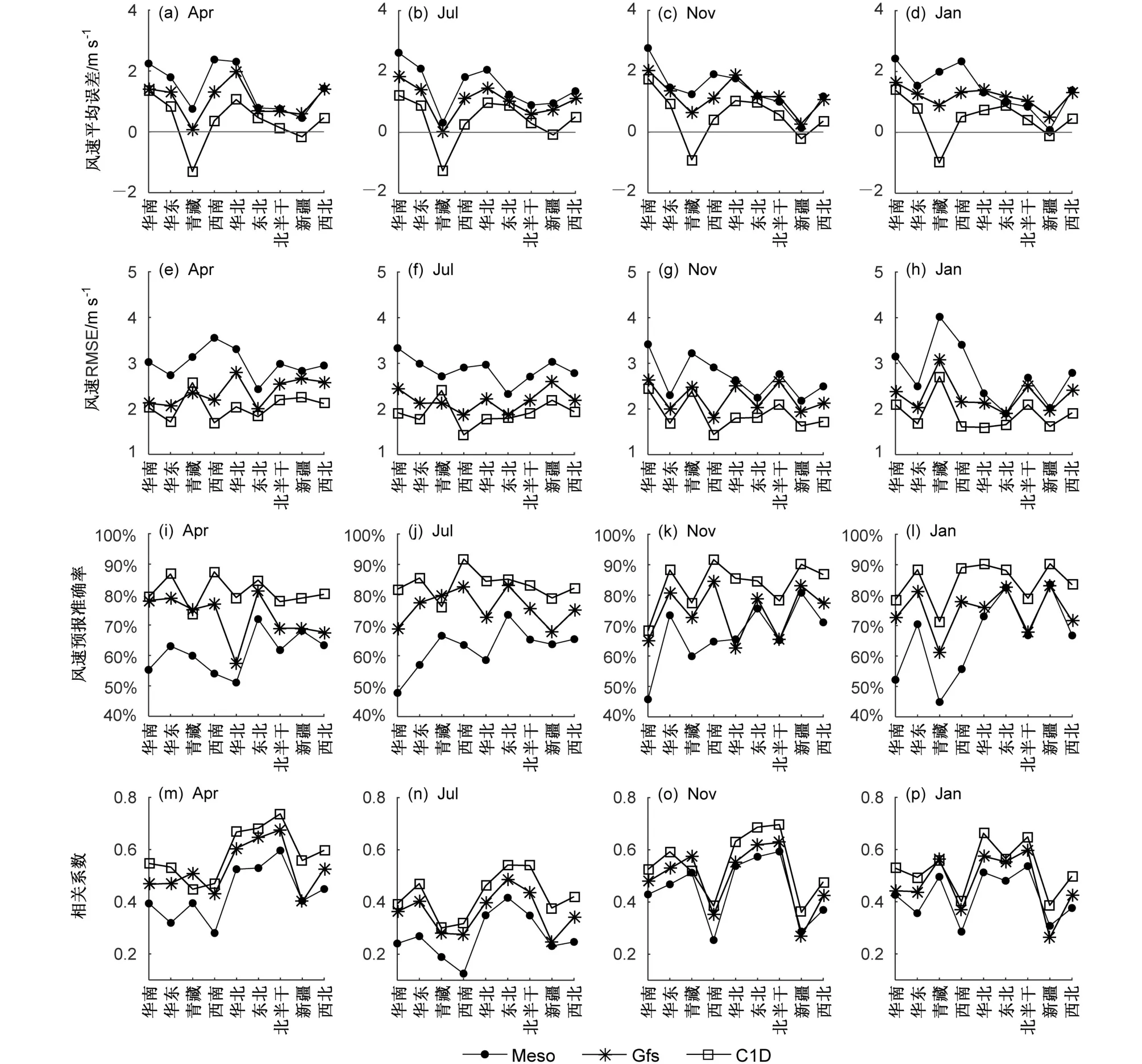
图9 Meso、Gfs、C1D数值模式模拟与观测风速在4月(第一列)、6月(第二列)11月(第三列)、1月(第四列)中国9个分区上各评估参数统计值:(a-d)平均误差;(e-h)均方根误差;(i-l)预报准确率;(m-p)相关系数Fig. 9 Evaluation parameters of the wind speed between the numerical model predictions (Meso, Gfs, and C1D) and observations in the nine subregions over China in April (first column), July (second column), November (third column), and January (fourth column): (a-d) ME; (e-h) RMSE;(i-l) the forecast accuracy of models; (m-p) correlation coeffcient
3.3.3 均方根误差日变化特征
图10给出不同时刻均方根误差的统计特征。可以看出,Gfs与C1D特征相似,均方根误差北京时间昼高夜低,Meso没有此特征,说明Gfs和C1D预报能力白天优于夜间。Meso随时效增长均方根误差增大,4月、7月增长趋势更明显,说明Meso随预报时效增长预报能力下降明显。3个模式4月均方根误差值高于其他季节。
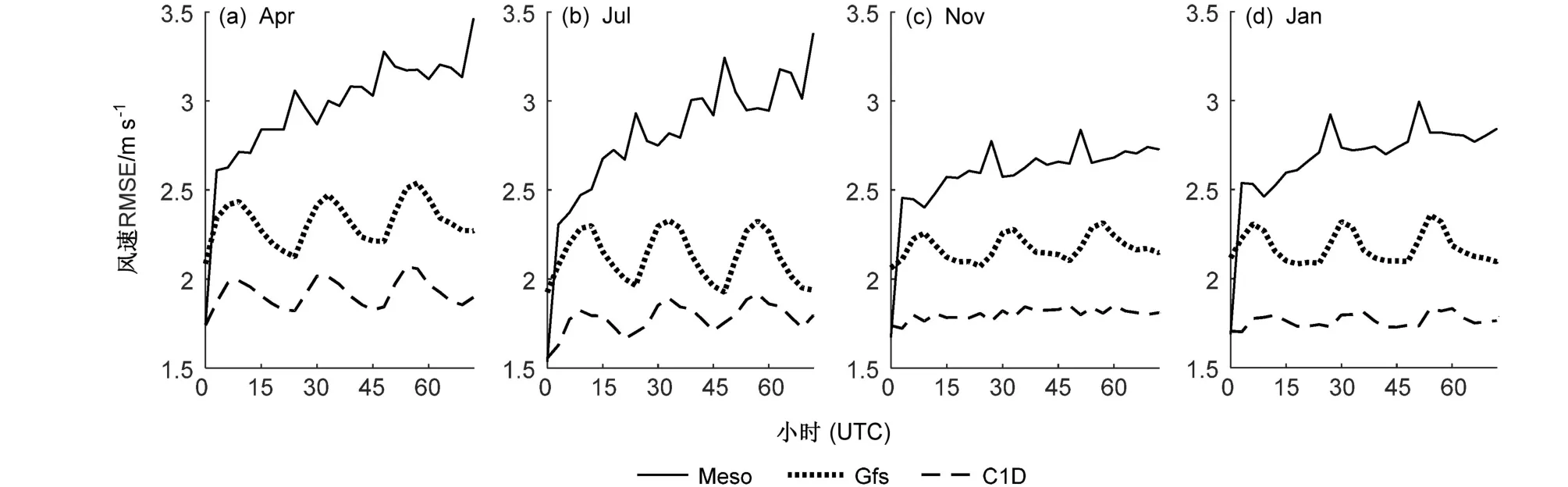
图10 Meso、Gfs、C1D数值模式模拟与观测风速均方根误差日变化特征:(a)4月;(b)7月;(c)11月;(d)1月Fig. 10 Diurnal variations of RMSE between the numerical model predictions (Meso, Gfs, and C1D) and observations of the wind speed: (a) April;(b) July; (c) November; (d) January
3.4 湿度
3.4.1 评估参数均值特征
表5给出数值模式与风速观测值的平均偏差、均方根误差、预报准确率和相关系数在不同月份和年统计值。综合误差概率分布情况和各评估参数的统计值可以发现:湿度误差集中在[-20%, 20%],此区间样本数量Meso和Gfs占总样本量70%以上,C1D在80%以上。与其他观测要素相比,3个模式湿度误差概率分布曲线的收敛度最差。Gfs平均误差为较大正值,Meso和C1D为负值。3个模式中C1D湿度的预报准确率最高,与观测资料的均方根误差最小,相关系数最大。Meso与Gfs的各评估参数值接近。说明湿度C1D预报能力最好,Meso与Gfs相似。3个模式均表现为7月均方根误差最小,预报准确率和相关系数最高的特征,说明3个模式均为夏季湿度预报能力最好。
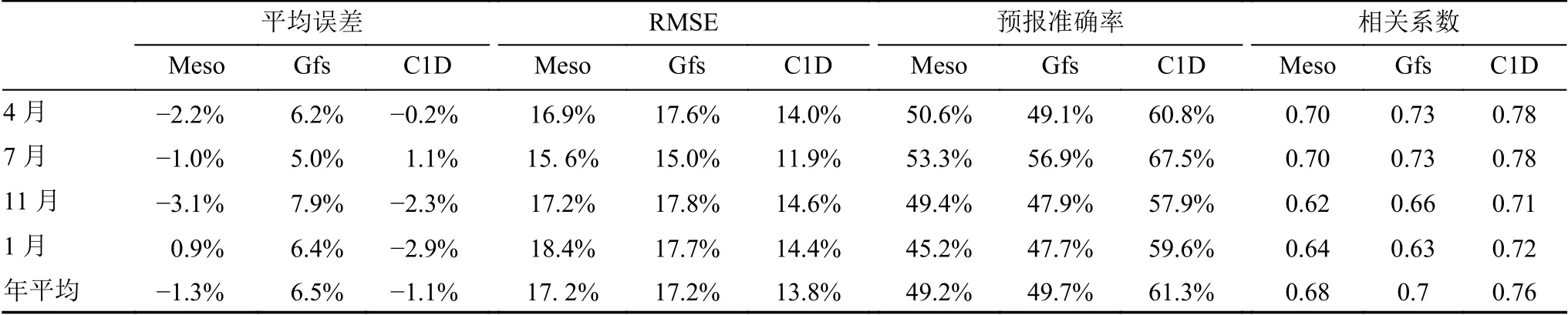
表5 数值模式模拟与观测湿度资料各评估参数统计值Table 5 Statistics of evaluation parameters of the humidity between the numerical model predictions and observations
3.4.2 评估参数空间分布特征
图11给出数值模式资料和湿度观测值的平均偏差、均方根误差、预报准确率和相关系数年均值的空间分布特征。图12给出不同评估参数在不同月份、不同区域的平均值分布特征。
综合图11和图12可以看出:3个模式平均偏差区域分布和月际间差异没有明显共性特征。Gfs在不同季节所有地区误差均为正值,Meso青藏和华北以北地区误差普遍为正值,华南、华东、西南和华北地区误差多为负值,C1D青藏地区误差为正值,华南、华东、西南地区误差多为正值且接近0,华北及以北地区误差多为负值。说明所有区域湿度预报Gfs易高估,华北及以南地区Meso预报易低估,C1D易高估,华北以北地区Meso易高估,C1D易低估。青藏地区3个模式均方根误差均明显高于其他地区,在20%左右;华南、华东、西南等地区3个模式均方根误差接近,普遍在10~15%;华北及以北地区C1D均方根误差仍在10%~15%, Meso和Gfs均方根误差偏高,在15~20%,且不同区域、不同季节间差异较大,没有明显规律。除1月外,青藏地区3个模式预报准确率均明显低于其他地区,小于50%;华南、华东、西南等地区3个模式预报准确率接近且高低顺序相同,C1D预报准确率最高,Gfs次之,Meso最低;青藏及华北以北地区C1D预报准确率仍为3个模式中最高,且各区域间差异较小,Meso和Gfs预报准确率在不同区域、不同季节各有高低,且各区域间差异较大。相关系数与均方根误差、预报准确率表现出相似的区域分布特征,4月3个模式间相关系数差异最小。3个模式空间分布特征差异较大,除青藏地区预报能力最差、东南地区预报能力最好外3个模式空间分布特征没有明显的共性,说明3个模式区域间预报能力差异很大。
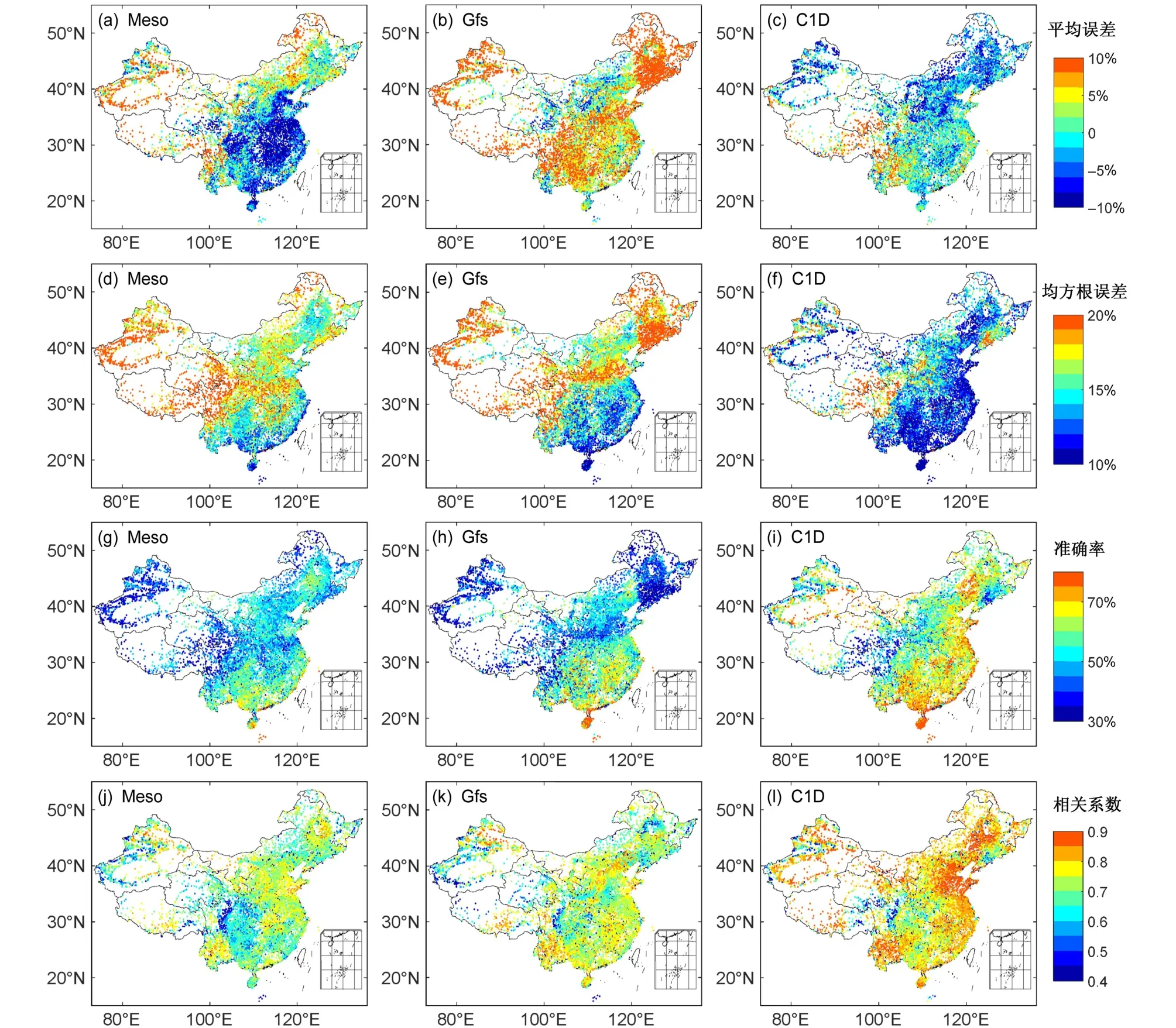
图11 Meso(第一列)、Gfs(第二列)、C1D(第三列)数值模式模拟与观测湿度评估参数的空间分布:(a、b、c)平均误差;(d、e、f)均方根误差;(g、h、i)预报准确率;(j、k、l)相关系数Fig. 11 Spatial distribution of evaluation parameters of the humidity between the numerical model predictions using Meso (the first column), Gfs (the second column), and C1D (the third column) and observations: (a, b, c) ME; (b, e, f) RMSE; (g, h, i) the forecast accuracy of models; (j, k, l)correlation coeffcient
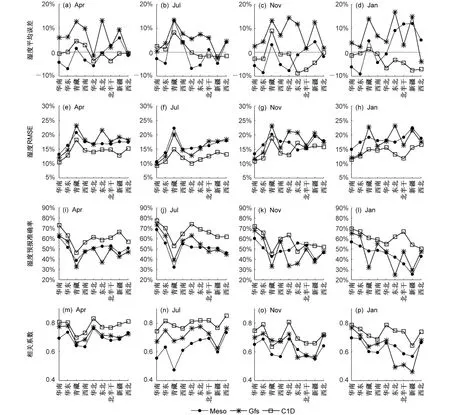
图12 Meso、Gfs、C1D数值模式模拟与观测湿度在4月(第一列)、6月(第二列)11月(第三列)、1月(第四列)中国9个分区上各评估参数统计值:(a-d)平均误差;(e-h)均方根误差;(i-l)预报准确率;(m-p)相关系数Fig. 12 Evaluation parameters of the humidity between the numerical model predictions (Meso, Gfs, and C1D) and observations in the nine subregions over China in April (first column), July (second column), November (third column), and January (fourth column): (a-d) ME; (e-h) RMSE;(i-l) the forecast accuracy of models; (m-p) correlation coeffcient
3.4.3 均方根误差日变化特征
图13给出不同时刻均方根误差的统计特征。可以看出,Meso与C1D特征相似,7月均方根误差北京时间昼高夜低(17:00出现最高值,08:00出现最低值),其他季节均方根误差北京时间05:00达到最高值,14:00达到最低值。Gfs所有季节均是北京时间白天均方根误差较大,夜间较低。
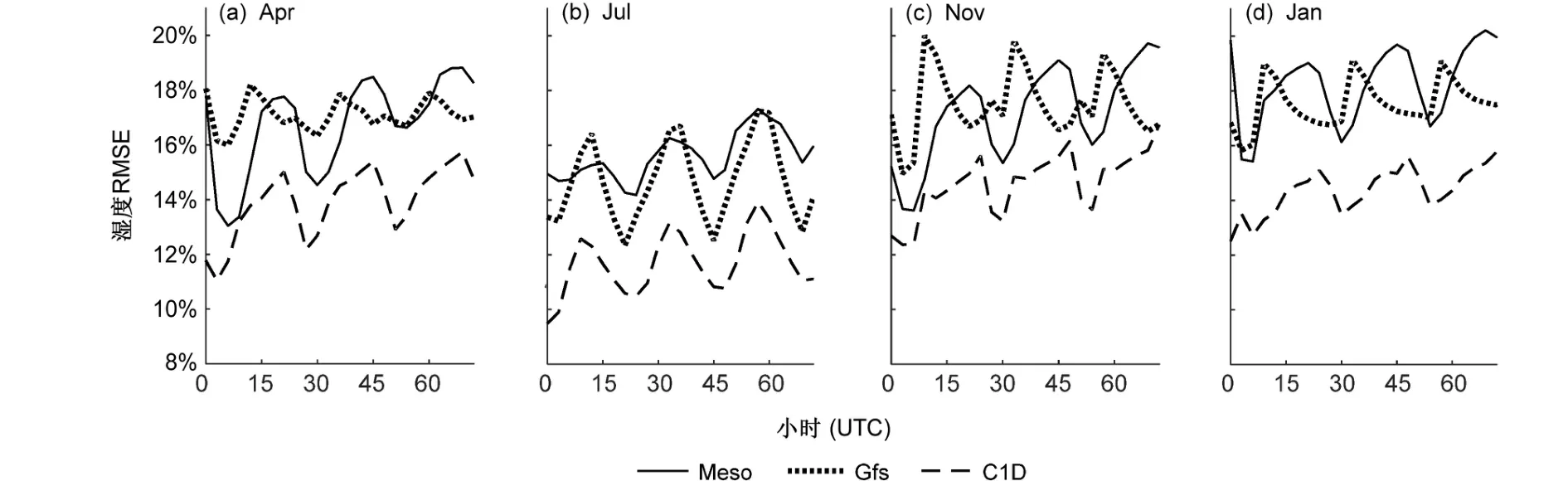
图13 Meso、Gfs、C1D数值模式模拟与观测湿度均方根误差日变化特征:(a)4月;(b)7月;(c)11月;(d)1月Fig. 13 Diurnal variations of RMSE between the numerical model predictions (Meso, Gfs, and C1D) and observations of the humidity : (a) April; (b)July; (c) November; (d) January
4 结论与讨论
本文分别利用中国气象局2421个国家级自动站和8155个地面天气站(骨干站)逐时观测资料对2017年7月和11月、2018年1月和4月的ECMWF确定性预报C1D、GRAPES_MESO、GRAPES_GFS的气温、地表温度、风速、湿度在中国区域的适用性进行了对比分析,得到如下结论:
(1)3个模式预报均存在系统误差。气温预报7月华北、东北等北部地区Meso和C1D易高估。除1月外,Gfs全国范围气温预报易低估,东北地区低估值最大。地表温度预报除1月新疆地区Gfs易高估外,其他时段3个模式预报在全国范围均易低估,Gfs低估值最大。风速预报除青藏地区C1D易低估外,3个模式预报易高估。湿度预报Gfs全国范围易高估,华北及以南地区Meso预报易低估,C1D易高估,华北以北地区Meso易高估,C1D易低估。
(2)所有分析的气象要素中,3个模式中C1D均方根误差最小、预报准确率最高、相关系数最大,说明C1D预报能力最好。Meso和Gfs在不同季节、不同区域预报能力各有千秋。地温预报Meso优于Gfs,风速预报Gfs优于Meso,气温、湿度预报Meso和Gfs相近。
(3)3个模式预报能力存在相似特征,但也存在一些差异。3个模式青藏地区预报能力均明显低于其他地区;气温和地表温度预报3个模式均表现为从东南向西北预报能力越来越差;风速预报华北以北地区3个模式预报能力相近,华北及以南地区差异较大,Meso预报能力显著偏低;C1D湿度预报能力各区域间差异较小,Gfs和Meso各区域间差异较大,且没有明显规律;3个模式华南、华东、西南、华北、东北等地区地表温度预报能力春夏季低于秋冬季。
(4)3个模式的均方根误差大多存在明显的昼夜变化特征。所有分析的气象要素中,3个模式均存随预报时效增长均方根误差增大的趋势。Meso气温、风速均方根误差没有明显的昼夜差异,且两个要素随预报时效增长均方根误差显著增大。除7月外,Gfs湿度的均方根误差昼夜变化特征与Meso、C1D差异明显。
(5)3个模式均为湿度预报准确率最低,Meso的地表温度预报准确率最高, Gfs和C1D风速预报准确率最高。3个模式与观测资料的相关系数均表现为气温的相关系数最高,风速的相关系数最小。
很多研究中表明ECMWF预报性能优于其他数值预报模式(刘静等, 2014; 张宏芳等, 2014; 龚伟伟等, 2015a, 2015b )。C1D为ECMWF确定性预报模式,本文研究指出了C1D与我国自主研发的数值模式Meso、Gfs相似特征和差异。可以看出,虽然现阶段Meso和Gfs整体预报性能低于C1D,但在一定程度上能够反映观测资料所具有的时空分布特征,具有一定的适用性。随着我国数值预报技术的不断提高,Meso和Gfs预报性能也会提升。本文仅使用4种基本的评估参数对3个模式部分气象要素的预报性能进行了评估,对造成预报性能差异的原因未做探究,在今后的工作中会结合模式机理和气象要素的物理特性进行针对性评估,并提出合理应用建议。

