关于坐标转换尺度系数计算的分析

秦 锋 张振虎

(1. 中国核工业集团三门核电有限公司 浙江 台州 317112;2. 上海勘察设计研究院(集团)有限公司 上海 200093)

0 引言

空间直角坐标转换需要计算七参数,包括尺度系数、旋转角度(旋转矩阵)及平移参数。目前坐标转换的算法主要分为两类,一类是基于经典最小二乘(least square,LS)的坐标转换算法,另一类是基于变量含误差(errors in variables,EIV)模型的整体最小二乘(total least squares,TLS)或加权整体最小二乘(weighted total least squares,WTLS)坐标转换算法。

尺度系数通常认为是两坐标系距离之比。在经典最小二乘准则下,小角度坐标转换一般采用线性最小二乘一次性计算出包括尺度系数在内的坐标转换七参数。对于基于经典最小二乘准则的大角度坐标转换,文献[1]论证了尺度系数和旋转矩阵(或旋转角度)之间不相关,和平移参数之间呈强相关,故大部分基于经典最小二乘准则的大角度坐标转换算法在计算坐标转换参数时先计算尺度系数,再计算旋转矩阵和平移参数。如文献[2]通过计算坐标转换前后所有距离比值的平均值来计算尺度系数,文献[3]对坐标数据重心化处理后采用最大似然估计计算尺度系数,文献[4]对坐标数据重心化处理后通过计算坐标转换前后重心化坐标平方和比值的开方值来计算尺度系数。另有部分基于经典最小二乘准则的大角度坐标转换算法一次性计算出坐标转换七参数,如文献[5]对误差方程线性化处理后通过迭代一次性求解坐标转换七参数,不需要分别计算尺度系数、旋转矩阵及平移参数。但在实际应用中发现,以上计算坐标转换尺度系数的方法计算结果互有差异,难以确定何种方法尺度系数计算结果最优。

在TLS或WTLS准则下,坐标转换参数中尺度系数的求解较LS准则下复杂。目前已有的TLS或WTLS坐标转换方法主要分为两类,一类是分别计算尺度系数、旋转矩阵及平移参数,另一类通过迭代一次性计算出全部参数。第一类方法中,如文献[6]采用多元总体最小二乘方法分别求解坐标转换参数,文献[7]推导了特定加权矩阵下采用多元总体最小二乘求解坐标转换参数的方法。第二类方法中,如文献[8]采用提出了一种基于TLS准则的小角度坐标转换算法,文献[9]采用改进的加权整体最小二乘算法用于小角度坐标转换,文献[10]提出了一种通用的加权整体最小二乘坐标转换方法。

本文通过奇异值分解算法(singular value decomposition,SVD)推导了LS及TLS准则下坐标转换尺度系数的计算公式,并结合工程实例,与其他尺度系数计算方法进行了对比。同时,为验证本文算法,采用了布罗伊登-弗莱彻-戈德法布-香农(Broyden-Fletcher-Goldfarb-Shanno,BFGS)优化算法进行结果验证。对于WTLS准则下坐标转换尺度系数的计算及其与旋转角度、平移参数之间的相关性,本文基于文献[10]中的方法进行了数据验证,并得出了相应结论。

1 数学模型及算法

坐标转换模型可表示为

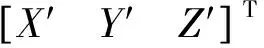
为方便参数计算,根据文献[11]对坐标进行重心化处理。数据重心化处理后,旋转矩阵和平移参数可分开进行计算,其计算公式为

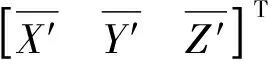
分别定义矩阵A和B为

重心化后的坐标转换模型就可表示为:A=λRB

1.1 基于LS准则的坐标转换尺度系数计算

求取正交矩阵R,使A-λRB的弗罗贝纽斯(Frobenius)范数最小时所得的R即为最佳转换矩阵,即求解以下问题，即

(5)

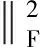
(6)

式中,tr是trace的简写,表示矩阵的迹。

因λ>0,故在tr(BATR)取最大值时,式(6)得到最小值。

对BAT进行奇异值分解,得

(7)

式中,U是左奇异矩阵;V是右奇异矩阵;Σ=diag(σ1,σ2,σ3),σ1,σ2,σ3为BAT的奇异值。根据文献[12],R=VUT时,tr(BATR)取最大值。将求得的R代入式(6),此时式(6)为关于λ的一元二次方程求极值问题,当λ为式(6)时,式(6)得到最小值。

(8)

平移参数可根据式(4)进行计算。

1.2 基于TLS准则的坐标转换尺度系数计算

考虑到矩阵A、B中的随机误差EA、EB,构建EIV模型为

(9)

假设随机误差EA、EB独立同分布,基于拉格朗日乘子法,构建整体最小二乘优化函数为

(10)

函数f分别对EA、EB、μ求偏导并置0,解出EA、EB、μ后代入式(10),得

(11)

同式(7),对BAT进行奇异值分解;同理,当且仅当R=VUT时,f取极小值。将R=VUT代入式(11)中,可得

(12)

式(2)对λ求偏导并置0,因λ>0,tr(Σ)>0,故可解出

(13)

平移参数可根据式(4)进行计算。

1.3 验证算法

分别定义以下矩阵:

其中,Ln表示元素全是1的列向量。

坐标转换模型又可表示为:

(14)

构建基于LS准则的坐标转换优化函数:

(15)

参照式(9)至式(11),构建基于TLS准则的坐标转换优化函数为

(16)

对上述两个函数分别采用BFGS算法进行优化,迭代求取坐标转换七参数。具体BFGS算法可参照文献[13]。

2 案例分析

坐标转换数据选用文献[10]中的数据,详细数据见表1。

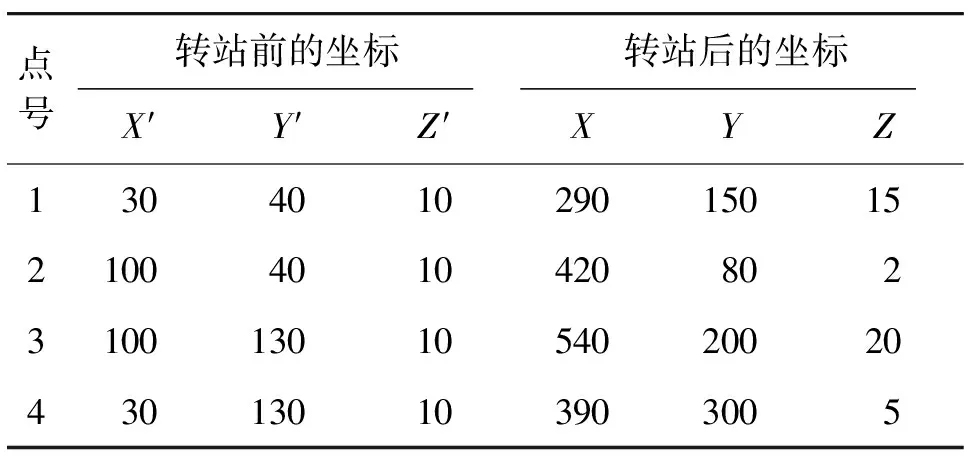
表1 坐标转换原始数据 单位：m

分别采用文献[2-5]中算法计算尺度系数,同时采用本文算法及验证算法分别计算LS准则下及TLS准则下坐标转换七参数,解算结果见表2。

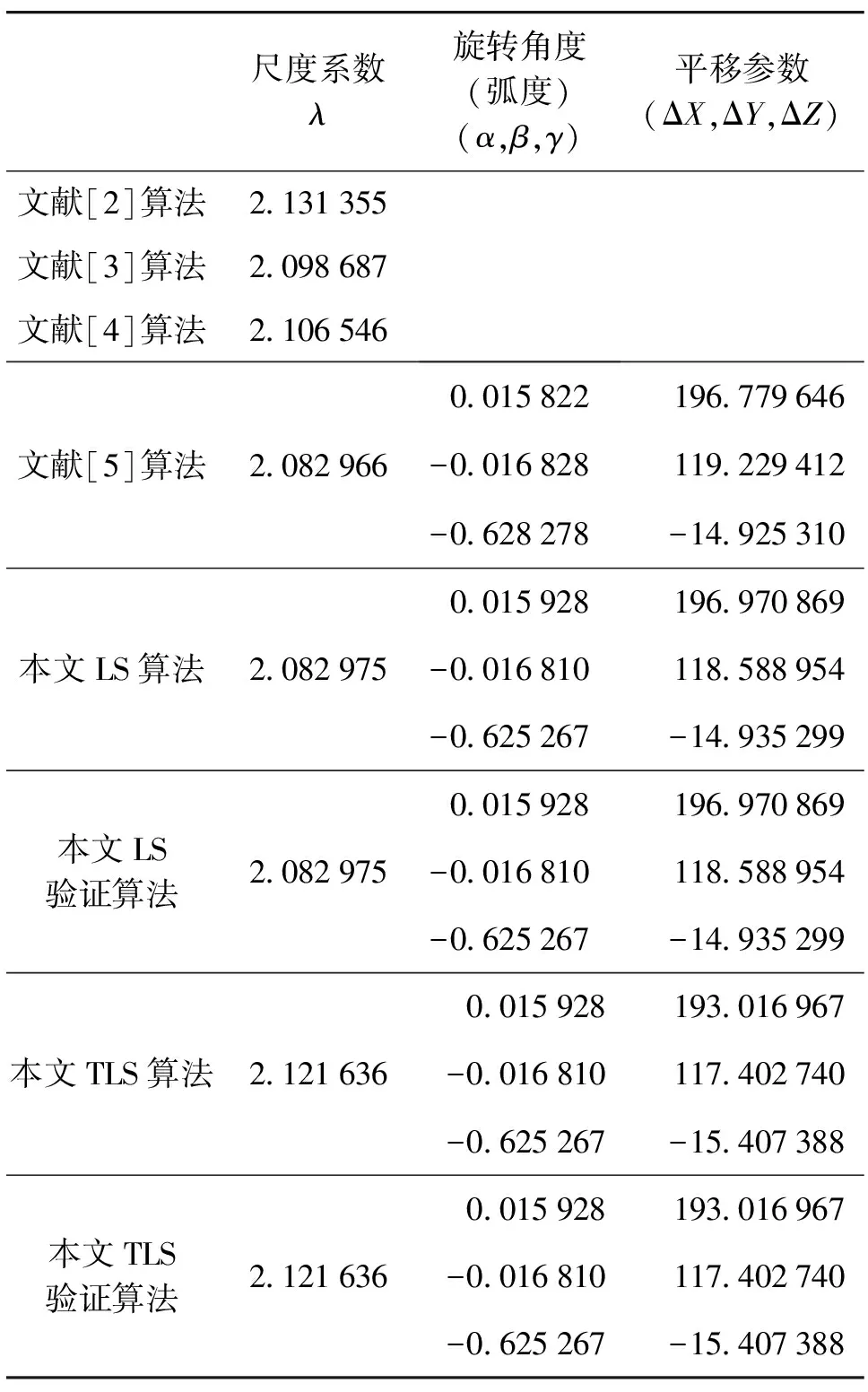
表2 LS及TLS准则下坐标转换参数解算结果

从以上计算结果可以看出:

(1)本文LS坐标转换算法与基于BFGS优化算法的LS坐标转换验证算法解算的七参数完全一致,而文献[2-5]尺度系数计算结果均与本文LS算法结果有差异,说明LS准则下本文提出的尺度系数计算方法更准确。

(2)在TLS准则下,本文算法解算的尺度系数也与验证算法解算结果一致,但与本文LS算法计算的尺度系数不一致,说明LS准则下尺度系数的计算方法并不能用于TLS准则下尺度系数的计算。

(3)比较上述案例LS准则下和TLS准则下坐标转换参数计算结果,可以发现两种准则下旋转角度计算结果完全一致,这与1.1节和1.2节推导结果一致。

3 相关性分析

3.1 LS及TLS准则下尺度系数分析

从LS准则下构建的优化函数式(6)及TLS准则下构建的优化函数式(11)可以看出,无论尺度系数取何值,函数取最小值时所求取的旋转矩阵均不变,说明在LS准则和TLS准则下坐标转换尺度系数和旋转矩阵(旋转角度)不相关;另根据式(4)可以看出,计算平移参数需要尺度系数及旋转矩阵,故平移参数与尺度系数是相关的,这与文献[1]中结论一致。

3.2 WTLS准则下尺度系数分析

“坐标转换尺度系数与旋转矩阵不相关,与平移参数相关”这一结论适用LS准则及TLS准则,但是否同样适用于WTLS准则,目前的研究较少,故对于WTLS准则下该结论是否成立需要进一步的验证。

为验证WTLS准则下尺度系数与旋转矩阵(旋转角度)、平移参数的相关性,设计了以下六组权阵,每组权阵下再分别计算三种坐标转换参数(第一种计算全部七参数;第二种和第三种分别指定尺度系数为1和2,计算坐标转换六个参数),具体权阵数据见表3。

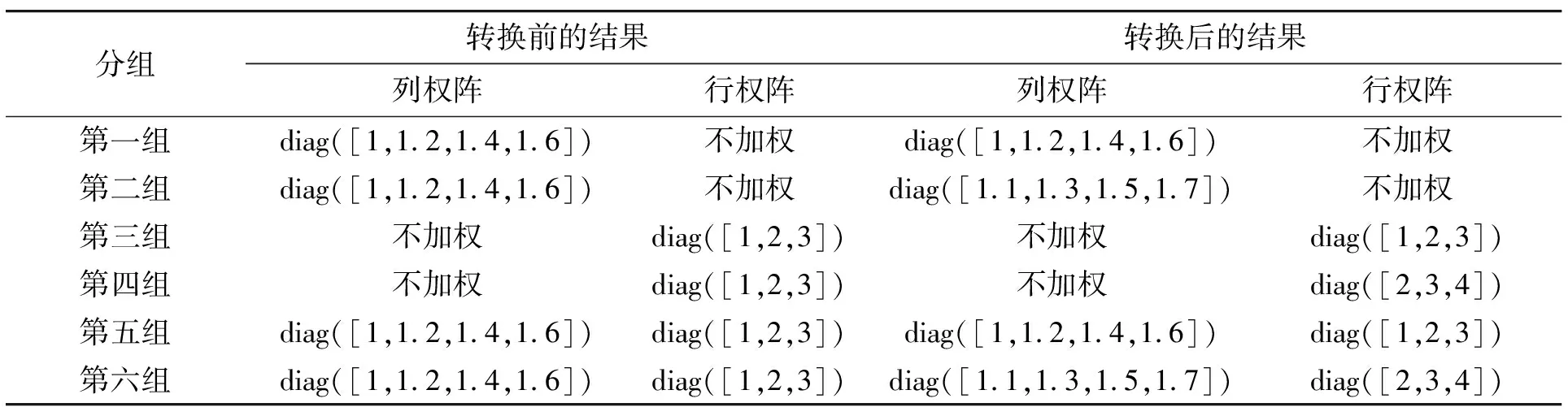
表3 WTLS准则下坐标转换设计权阵

坐标转换数据采用第3节案例分析中数据,并采用文献[10]中算法进行坐标转换参数解算,解算结果见表4。

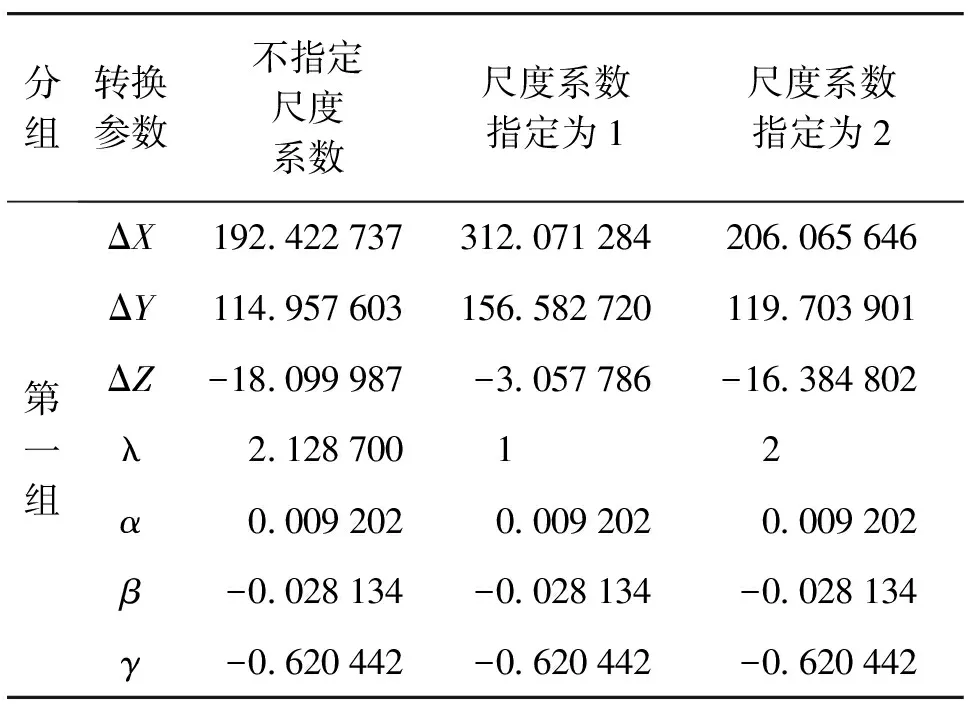
表4 WTLS准则下坐标转换参数解算结果

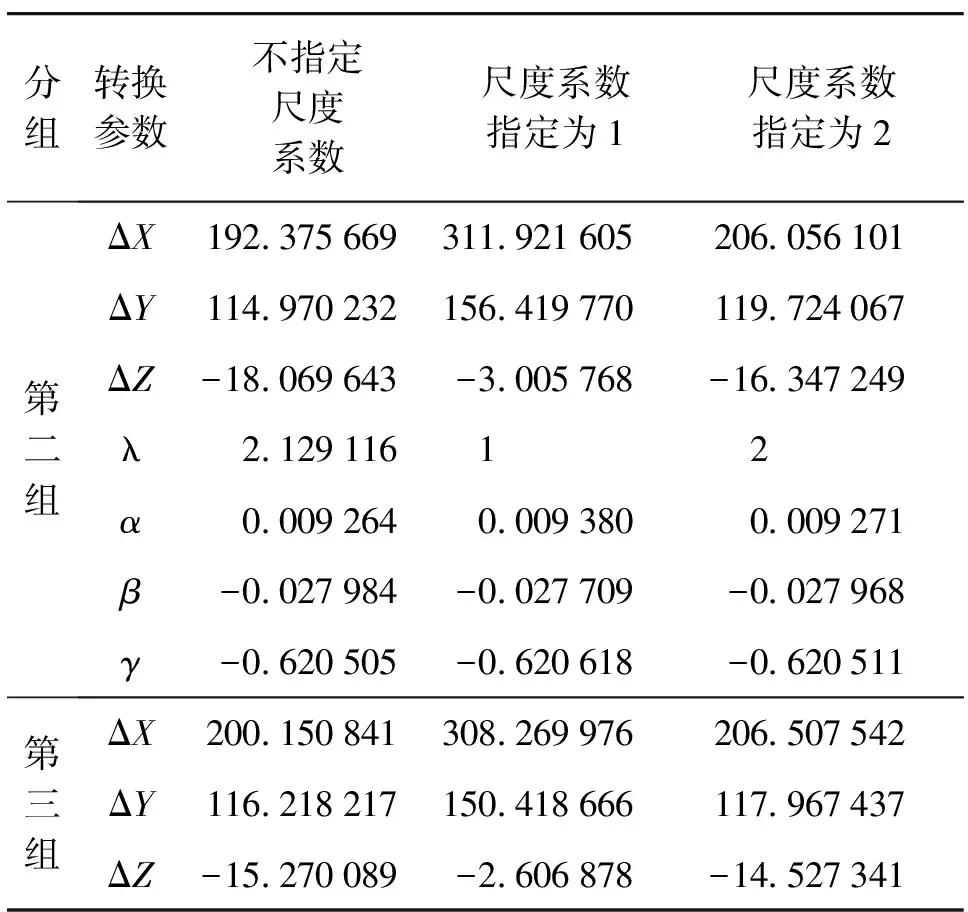
续表4

续表4

备注：所求得的角度均为弧度。

从表4计算结果可以看出,第一组权阵下,即对1.3节中矩阵C、D进行列加权、行不加权且列加权矩阵相同,当尺度系数变化时,旋转角度不变,平移参数改变,说明在第一组权阵下尺度系数与旋转角度不相关,与平移参数相关。第二组至第六组权阵下,尺度系数变化时,旋转角度及平移参数均改变,说明在这些权阵下尺度系数与旋转角度及平移参数均相关。

4 结束语

本文基于奇异值分解(SVD)算法推导了LS准则下和TLS准则下坐标转换尺度系数计算方法,并结合案例采用BFGS优化算法进行了验证,同时分析了LS、TLS及WTLS准则下坐标转换尺度系数与旋转角度、平移参数之间的相关性,并得出了以下结论:

(1)本文提出的LS准则下及TLS准则下尺度系数公式与最优化验证算法计算结果完全一致,说明本文方法可用于尺度系数的精确计算。

(2)对比LS及TLS准则下的坐标转换七参数计算结果,其旋转矩阵(旋转角度)相同,尺度系数不同,因尺度系数不同导致平移参数不同。

(3)在LS准则及TLS准则下,坐标转换尺度系数和旋转矩阵(旋转角度)不相关,与平移参数相关;但在WTLS准则下,除个别特殊权阵外,尺度系数与旋转矩阵和平移参数均相关。故在LS准则下及TLS准则下,坐标转换尺度系数、旋转矩阵及平移参数可分别计算,而在WTLS准则下坐标转换七参数不能分别计算(个别特殊权阵除外),只能通过优化算法迭代一次性求取全部七个参数。