非稳定供水下喷灌机管道压强变化规律的试验研究

张宝旭，朱德兰

（1.西北农林科技大学水利与建筑工程学院，陕西杨凌712100；2.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌712100）

0 引 言

喷灌以其节水增产、适应性广、操作方便、易于规模作业等优点，成为当今世界上最为广泛应用的灌溉方法之一[1]。到2015年全国喷灌工程的总面积已达到近0.5 亿亩，大约占我国节水灌溉总面积的20%[2]。在实际灌溉时，通常采用恒压稳定水源进行灌溉，但有时会使用非常规的水源进行供水，来提升整体灌溉质量。

Li Qiang[3]曾采用正弦型的动态水压进行灌溉，发现此供水条件下，对于缓解滴头堵塞问题有明显帮助；葛茂生[4]在波动供水下，研究了非旋转式喷头的喷洒情况；Zhang Kai[5]曾采用动态水压中的正弦型水源进行移动喷灌试验，发现采用正弦型水源供水时整体喷灌均匀度得到提升；付博阳[6]和任乃望[7]同样采用非稳定的供水方式对坡地喷灌进行改进，结果表明当使用波动水压进行坡地喷灌时，整体均匀度得到提升；陶帅[8]等人使用PWM 独立变量控制，改变喷灌机喷头流量的大小，提高了灌溉水的利用效率。

但在日常使用中，为喷灌机供水的水源并不总能保持恒压或规律性变化，导致喷灌机入口处压强流量均存在一定的随机波动，影响运行效果。而在轻型平移式喷灌机中的多孔管的水力性能较相较于传统直管为复杂[9]，压强分布规律较不明显[10]，故本文通过实物试验的方法研究在非稳定供水的条件下，不同喷嘴尺寸和变频泵运行频率对于喷灌机入口及内部的压强分布的影响，以期为当水源条件较差时的喷灌机应用提供指导。

1 试验材料与方法

1.1 试验材料

试验在西北农林科技大学旱区节水农业研究院进行，试验装置主要包括：非稳定供水的给水栓、变频泵、变频控制柜、非旋转折射式喷头、轻型平移式喷灌机、压强传感器、电磁流量计以及笔记本电脑等数据采集装置，整体装置示意图见图1。

由于本研究只关注喷灌机内部的压强分布规律，故采用固定喷洒的工作方式。试验中喷灌机可分为两段：入口段与出流段。入口段为喷灌机入口至两侧出流管前的管段，入口管道直径为65 mm，由多种连接件构成，在图1 中为A 点到B点，两侧对称；出流段由两侧水平出流管组成，为变径且开孔均匀的多孔出流管，从中心向两侧分布，共3种直径，依次为：60、50、40 mm，在图1 中起始点为B 点。出流段两侧对称，共34个喷头，喷头间距为1 m，单侧长度17.4 m。对于压强传感器的安装位置，采用间隔布置，在进入喷灌机出流段后，在首端布置一个压强传感器，正式进入管段后，每间隔一个出口处布置一个压强传感器，同时在末端额外安装一个压强传感器。

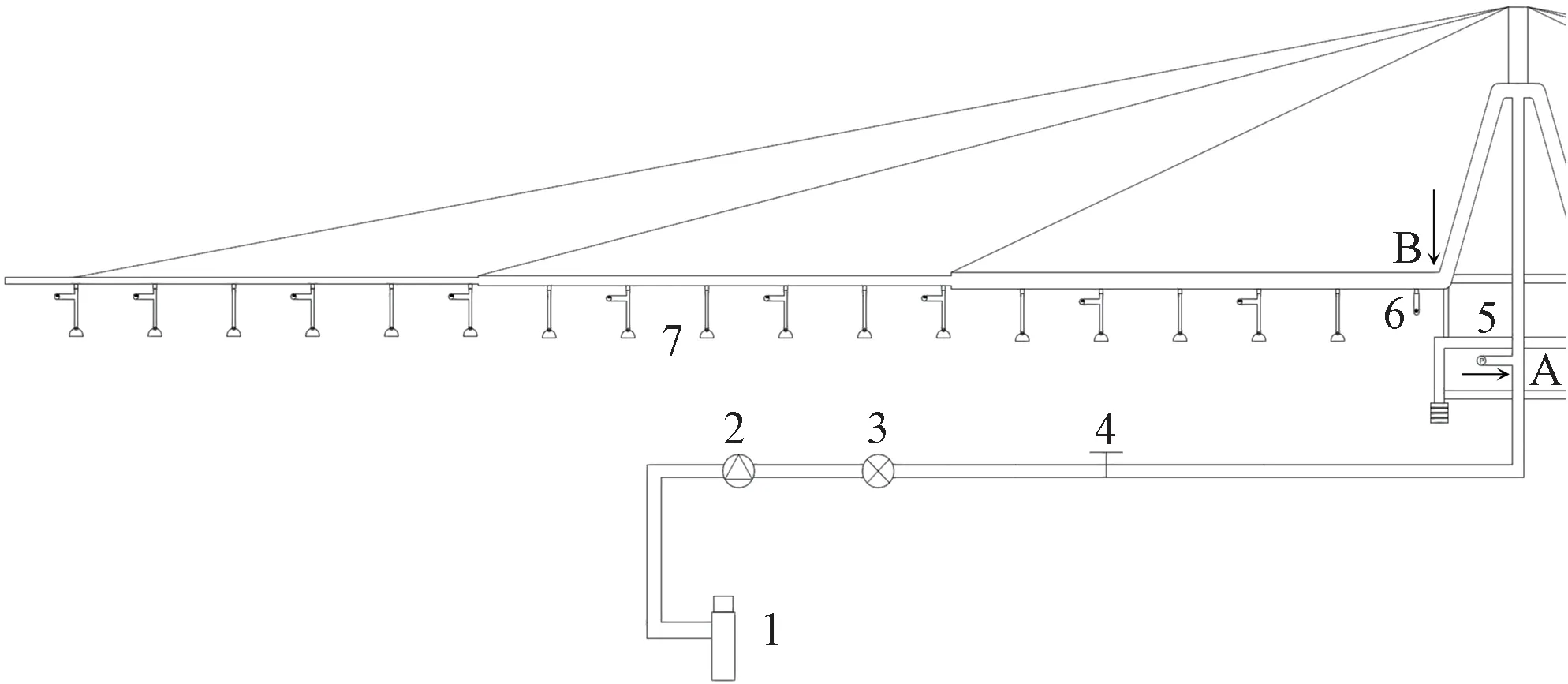
图1 试验装置示意图Fig.1 Schematic of the test setup

1.2 试验设计与监测指标

试验通过改变喷灌机入口处的变频泵运行频率控制喷灌机入口处的压强范围，同时改变喷嘴尺寸调节管道内的水力情况，其详细因素水平设置见表1。

表1 试验因素水平Tab.1 Test factor level

试验中喷灌机喷头距地面0.4 m，且喷灌机固定。试验中主要的监测指标为各点处的压强水头与喷灌机入口处的流量数据，数据在笔记本电脑中保存显示，保存间隔为1 s，单组试验进行3 min。在本文中，将使用MATLAB 编程对所得到的瞬时压强数据进行处理，得到每组试验中各位置压强水头的平均值、标准差、变异系数等参数。

2 结果与分析

2.1 水源非稳定性研究

本文中的非稳定供水相较于正常的稳定供水工况，其主要的特征为波动的幅度较大，且随机性较强。选取了6 mm 喷嘴、变频泵未运行的试验组中喷灌机入口处的瞬时压强与试验室内测得的普遍情况下的稳定的瞬时压强进行对比，见图2。

在图2 中，常规稳定供水得到的压强水头并非为一条直线，也存在小幅度的波动，但其变化幅度较小，其平均值为2.63 m，整体变异系数为0.56%，在试验与计算中常按照恒定流来处理。而本研究中的非稳定供水，其压强水头变化幅度较大，且变化幅度较为随机，平均压强水头为2.61 m，与稳定供水情况相近，但其平均振幅达到了0.15 m，最大振幅达到了0.32 m，变异系数为4.91%。其他喷嘴尺寸下喷灌机入口处的各组压强水头情况见表2。

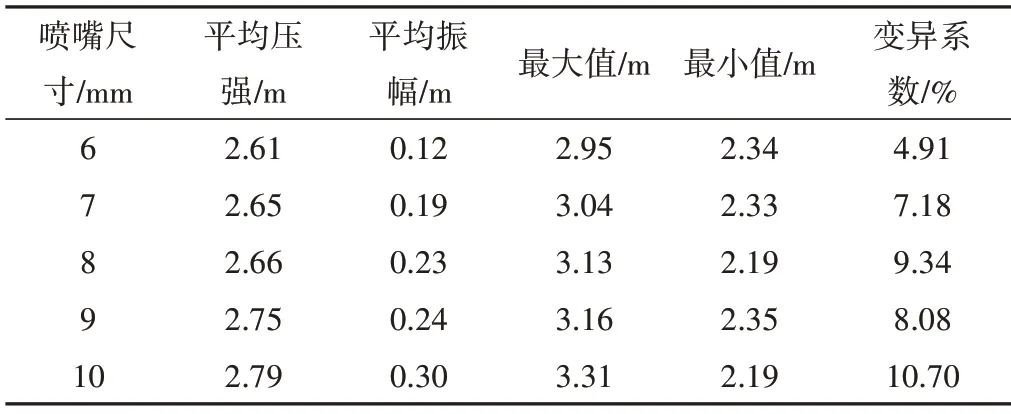
表2 变频泵未运行时入口压强水头数据Tab.2 Inlet pressure data when the inverter pump is not running

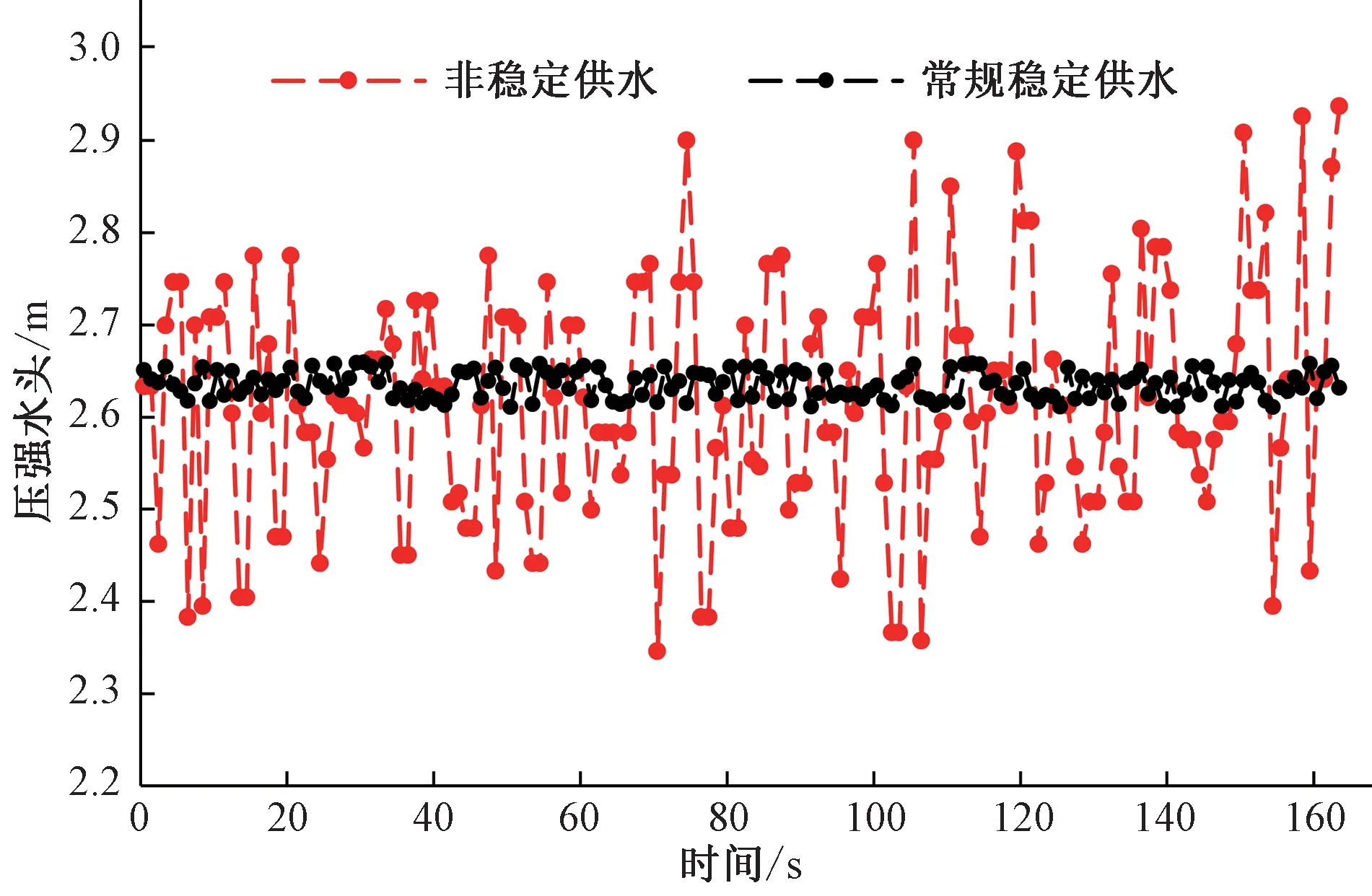
图2 6 mm喷嘴喷灌机入口处瞬时压强分布Fig.2 Instantaneous pressure time distribution at the inlet of 6 mm nozzle sprinkler

当喷嘴尺寸增大时，喷灌机入口处的平均压强与平均振幅均有小幅提升，同时变异系数的增大较为明显。为进一步研究喷灌机入口处压强变化，将对变频泵开启后的试验数据进行分析。

非稳定水源的一项重要水力特性就是平均压强水头，其数值大小决定了喷灌机整体的运行效果。在本试验中，影响因素主要为喷嘴尺寸以及变频泵运行频率，变频泵运行后喷灌机入口处平均压强水头的变化见图3。

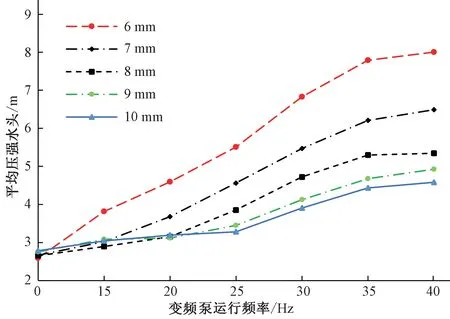
图3 喷灌机入口处平均压强水头变化Fig.3 Average pressure head variation at sprinkler inlet

从图3可以看出，喷灌机入口处的平均压强水头随变频泵运行频率的提升而增大，但平均压强水头的增长幅度随喷嘴尺寸的增大而逐渐减小，喷灌机入口处平均压强水头从0 Hz到40 Hz的增长数值分别为：5.41、3.82、2.69、2.17、1.80 m。同时变频泵在35 Hz 与40 Hz 频率运行时，各喷嘴尺寸下的喷灌机入口平均压强较为接近，这主要与喷灌机入口处的流量有关，其流量变化见表3。

在表3 中，各个喷嘴尺寸下，当变频泵运行频率相同时，喷灌机入口流量也基本一致，同时随着变频泵运行频率的提升，喷灌机入口的流量也逐渐增大，但当运行频率为35 Hz、40 Hz 时流量较为接近，此时已达到给水栓所能提供的最大流量，无法继续提升。

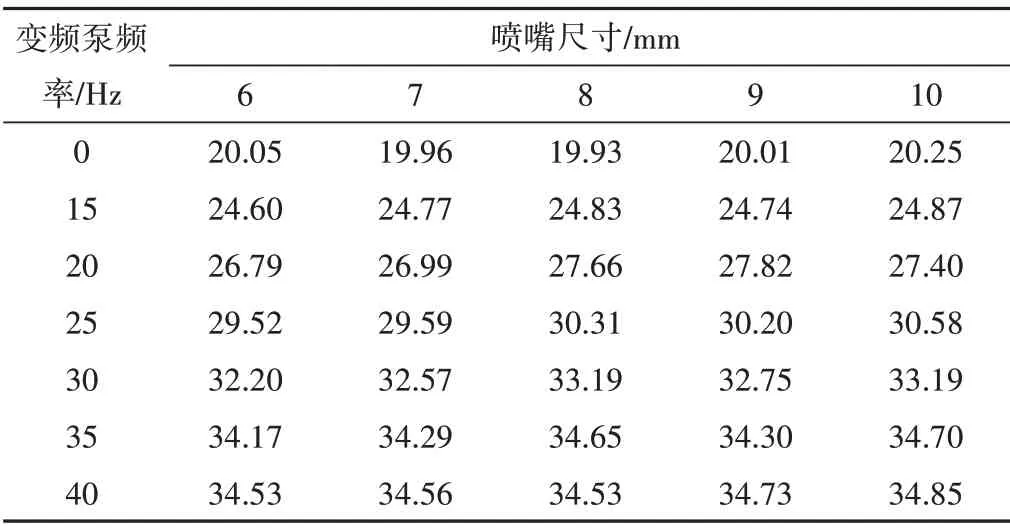
表3 变频泵入口处流量变化 m3/hTab.3 Variation of flow rate at the inlet of the variable frequency pump

对于水源的波动特性，本文中主要对波动平均压强水头振幅进行分析，平均压强水头振幅计算方法见下式[5]。

通过公式(1)和(2)计算处理后各组试验中喷灌机入口处的平均压强水头振幅随变频泵运行频率的分布见图4。

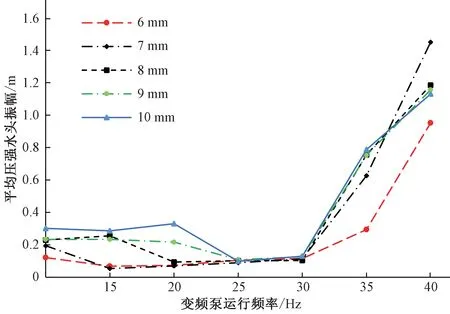
图4 喷灌机入口处平均压强水头振幅变化Fig.4 Variation of average pressure head amplitude at sprinkler inlet

随着变频泵运行频率的提升，平均压强水头振幅呈先小幅度减小后增大的趋势。变频泵未运行时，其波动均来自于给水栓的自身波动；变频泵低频运行时（15～30 Hz），其平均波动振幅减小，变频泵起到调节效果；当变频泵频率为35 Hz与40 Hz时，整体振幅明显增大，此时由于水源流量无法满足喷灌机的工作需求，导致整体波动增大。同时喷嘴尺寸对于喷灌机入口处振幅变化的影响较小，当喷嘴尺寸增大时，0～25 Hz阶段内振幅减小幅度越大，但在30～40 Hz阶段内增长幅度较为接近。

根据试验监测以及处理得到的平均压强与平均压强振幅数据，并结合喷灌机入口流量等其他参数，能够得到喷灌机入口处平均压强水头与平均压强水头振幅的拟合模型。对于入口处平均压强水头的拟合，选取平均入口流速与喷嘴尺寸作为自变量，通过MATLAB 软件拟合得到其数学模型，见下式[11]。

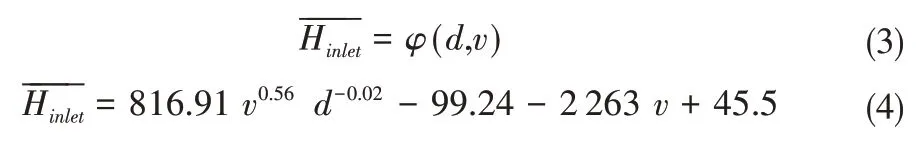
对于入口处的平均压强水头振幅的拟合，选取入口流速、喷嘴尺寸、平均压强水头作为自变量，采用同样的方式进行拟合[11]，见下式：

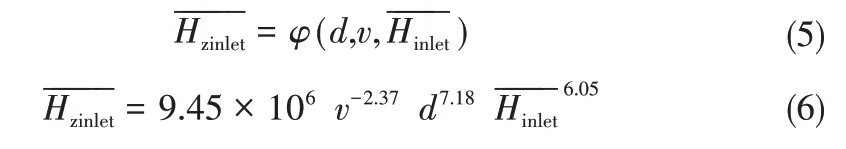
将拟合结果与试验数据进行对比，见图5。入口处的平均压强水头与平均压强水头振幅的拟合结果与实际较为接近，具有一定的代表性。

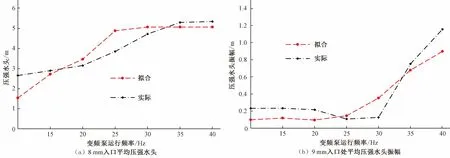
图5 喷灌机入口处压强水头拟合验证Fig.5 Verification of pressure head fitting at sprinkler inlet

2.2 喷灌机内压强分布规律研究

前文分析了喷灌机入口处的压强变化，由于喷灌机两侧对称，故仅对喷灌机内部单侧管道的压强分布进行研究。首先针对在不同喷嘴尺寸下喷灌机内部各位置处的平均压强及平均压强损失进行对比分析，选取了喷嘴尺寸6 mm与9 mm配置下喷灌机内的平均压强水头的分布情况，见图6。图6 展示的监测位置分别为喷灌机入口、出流管入口以及出流管中距入口不同距离的各测点。

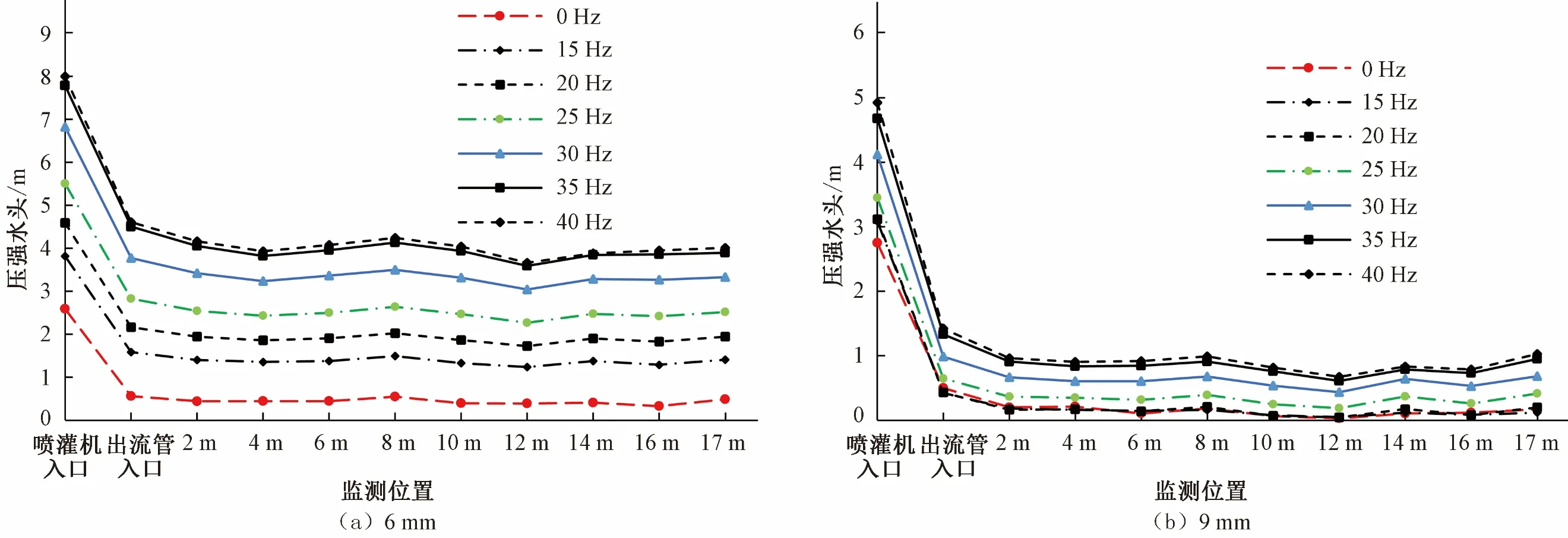
图6 喷灌机内部平均压强水头分布Fig.6 Average pressure head distribution inside sprinkler

图6不同配置下各组内喷灌机内部的压强分布规律较为一致，整体压强大小与变频泵运行频率呈正相关关系，且当喷嘴尺寸变大后，变频泵对喷灌机内压强的提升效果变小。为进一步观察喷嘴尺寸对于喷灌机内压强水头分布的影响，选取了变频泵运行频率25 Hz下不同喷嘴尺寸配置的压强水头分布进行比较，见图7。

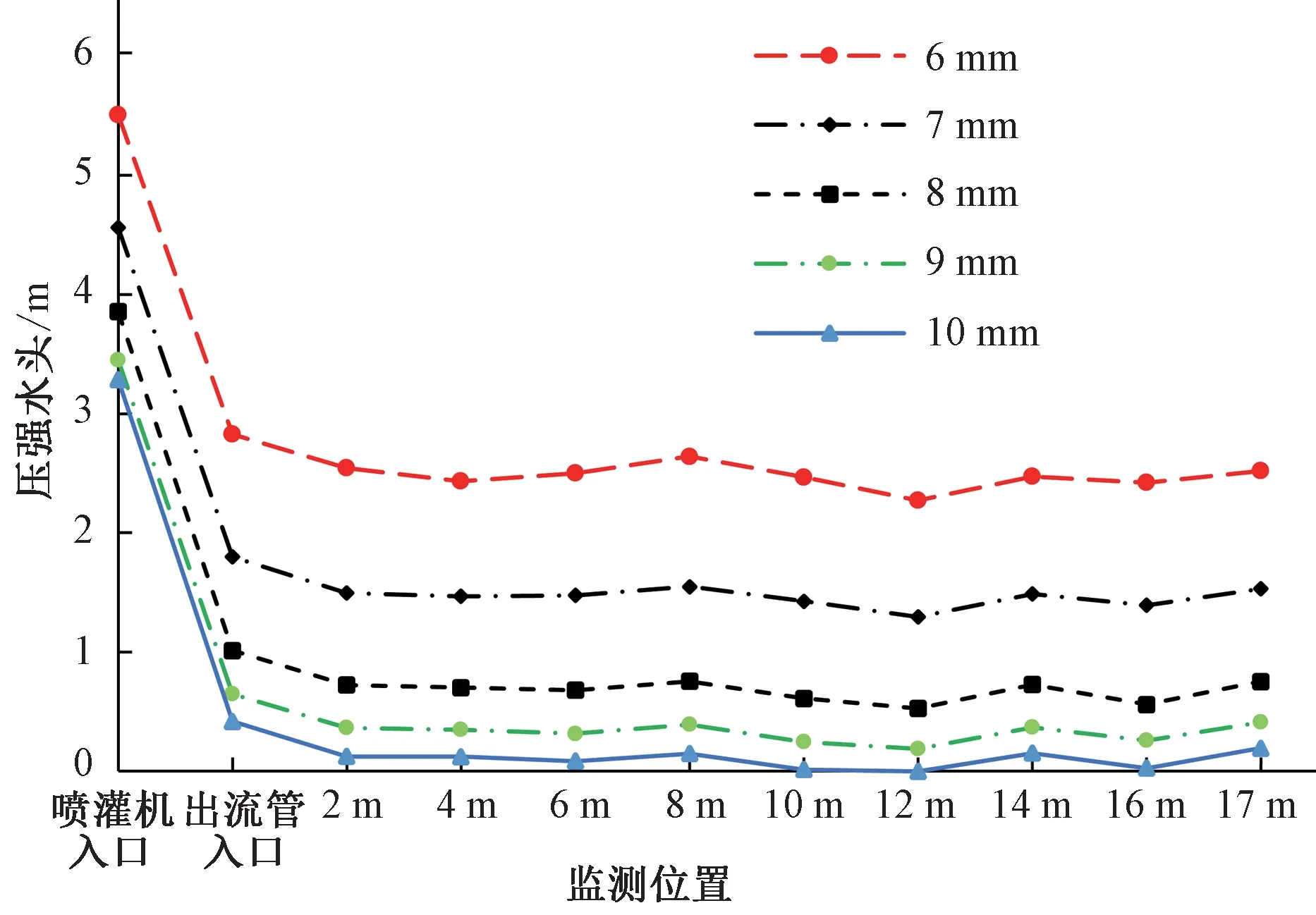
图7 喷嘴尺寸对管内平均压强水头分布影响Fig.7 Effect of nozzle size on the average pressure head distribution in the tube

当变频泵运行频率不变而增大喷嘴尺寸时，喷灌机内的压强水头逐渐降低，同时各组内的水头损失规律也相近，在进口段内由于连接管件较多，水头损失较大，而在出流段，每组平均压强损失较小。喷嘴尺寸与变频泵运行频率对平均压强损失的影响，见图8。

图8 中，当变频泵运行频率较小（0、15、20 Hz）时，各尺寸下的平均压强损失随着喷嘴尺寸的增大而增大。但随着频率的升高，各喷嘴尺寸下的平均压强损失的差距逐渐减小。为进一步探究管道内的平均压强整体损失情况，根据Zhang Kai[11]与E.B怀利[12]的分析方法，对从喷灌机入口至出流段尾端的损失量进行数值拟合，以喷灌机入口流速，喷灌机入口平均压强、喷嘴尺寸、及管道内位置为自变量，得到喷灌机两段的平均压强水头损失，见下式：

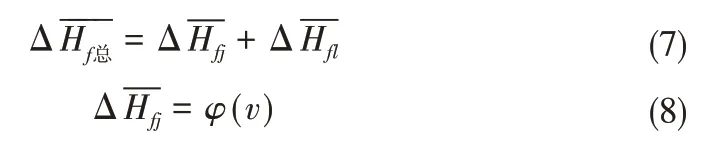
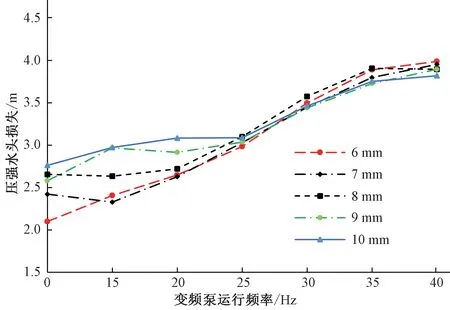
图8 喷灌机总平均压强水头损失Fig.8 Sprinkler total average pressure head loss

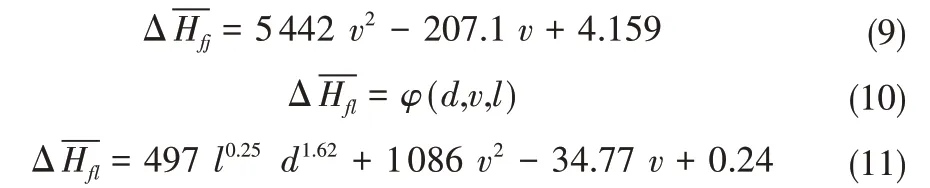
对于波动特性中的平均压强振幅这个指标，喷灌机内的分布与平均压强规律相近，平均压强水头振幅在喷灌机内的分布情况见图9。

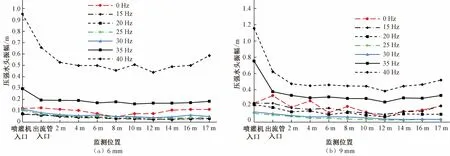
图9 喷灌机内部平均压强水头振幅分布Fig.9 Average pressure head amplitude distribution inside sprinkler

从图9发现，平均压强水头振幅在入口段的损失较大，进入出流段后，损失量较小。喷灌机内部的平均压强水头振幅随变频泵运行频率提升呈先减小后增大的变化趋势。为了观察喷嘴尺寸对平均压强振幅的影响，在图10 展示变频泵运行频率为25 Hz 时不同喷嘴尺寸下平均压强水头振幅的分布情况。

从图10 可以发现不同喷嘴尺寸下的压强水头振幅的分布较为接近，具体的损失规律可以采用数值拟合的方式建立对于喷灌机内平均振幅损失的分布模型。同样对喷灌机内部进行分段处理，得到入口段与出流段的平均压强振幅损失的分布模型[13]，见下式：

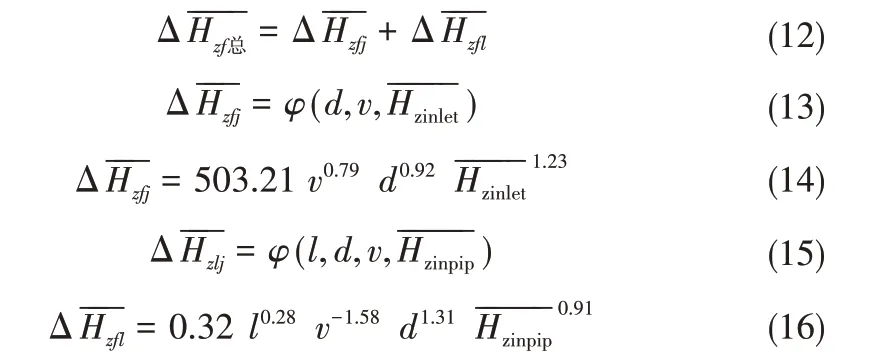
为验证拟合效果，以6 mm 尺寸喷嘴、变频泵运行频率20 Hz 下的平均压强水头损失与平均压强水头振幅损失为例，将拟合数据与实际试验数据进行对比，见图11，结果显示整体拟合度较好，具有实际应用价值。

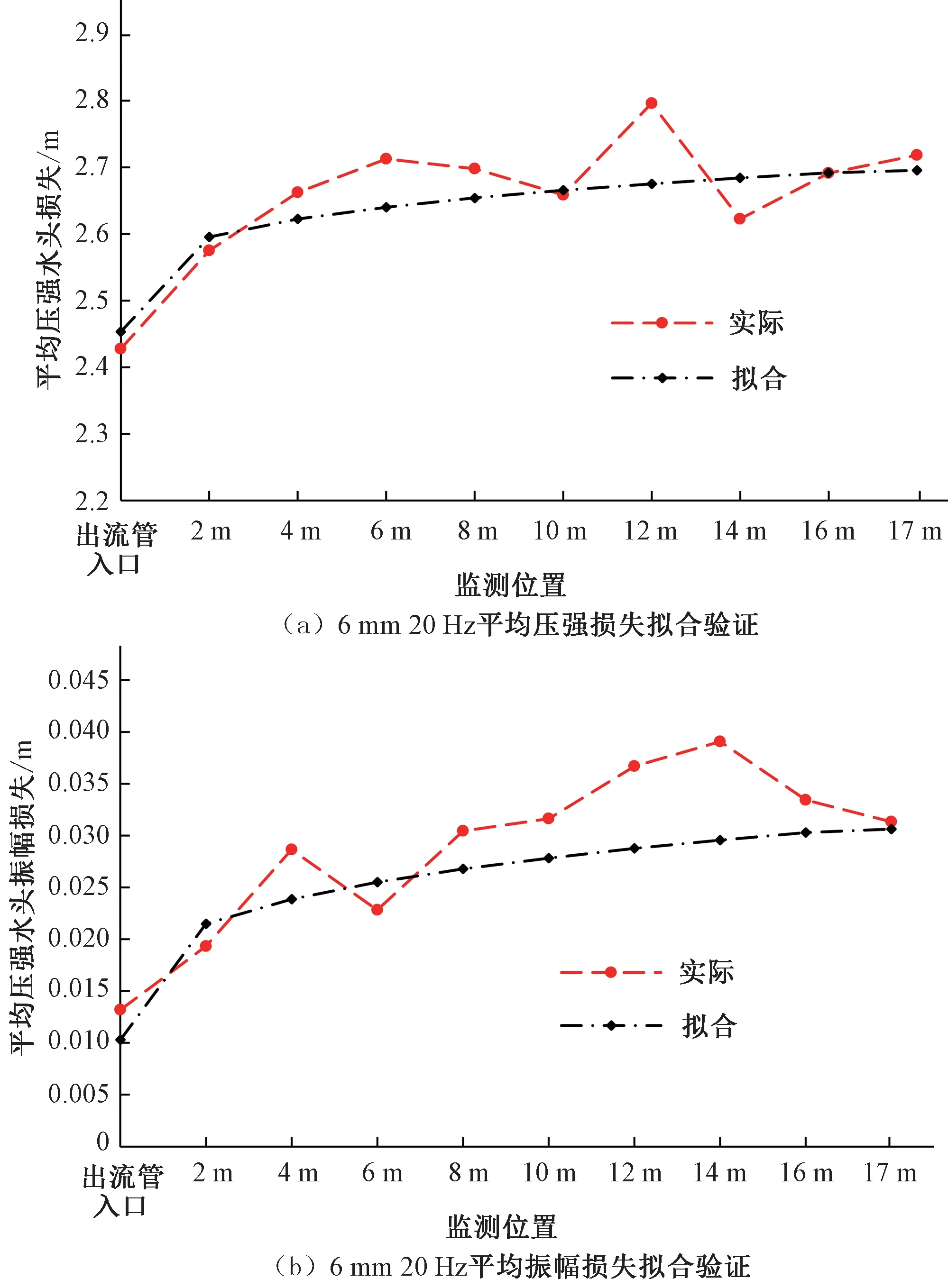
图11 喷灌机内部压强水头损失拟合验证Fig.11 Sprinkler internal pressure head decay fitting validation

3 结 论

本文主要目的是研究在水源不稳定情况下，喷灌机入口以及内部的压强变化规律，经过数据处理分析，得到如下结论：

（1）本研究使用的水源随机波动性较强，当变频泵未运行时，喷灌机入口处的压强的变异系数最大达到了10.72%。

（2）变频泵运行频率固定时，喷灌机入口处的平均压强随着喷嘴尺寸的增大而减小；平均压强振幅受喷嘴尺寸影响较小。喷灌机入口处平均压强随变频泵运行频率的增大而增大；平均压强振幅则呈先减小后增大的趋势。

（3）在喷灌机内部，增大喷嘴尺寸时，管道内平均压强逐渐降低；平均压强振幅变化较不明显。水泵运行频率对平均压强与平均压强振幅的影响与喷灌机入口一致。

（4）根据试验数据建立喷灌机入口及喷灌机内部的平均压强与平均压强振幅的拟合模型，经对比验证拟合精度较高。