CS-Softmax:一种基于余弦相似性的Softmax损失函数
张 强 杨吉斌 张雄伟 曹铁勇 郑昌艳
1(陆军工程大学研究生院 南京 210007)
2(陆军工程大学指挥控制工程学院 南京 210007)
3(火箭军士官学校 山东青州 262500)
(zq308297543@126.com)
卷积神经网络(convolutional neural networks, CNNs)能够准确建模高维嵌入表示参数的局部分布,被广泛应用于许多视觉与听觉分类任务中,如声学场景分类[1-3]、物体识别和分割[4-10]、人脸验证[11]、手写字符识别[12]等.然而在一些多分类问题中,由于不同类别的样本间存在较强相似性,CNNs分类框架的性能还不能令人满意[13].近年来,研究人员分别针对CNNs分类框架中的嵌入表示学习和分类2个方面,提出了许多有效的改进方法,进一步增强了分类效果.
在嵌入表示学习方面,CNNs的结构、激活函数[14-15]以及学习策略[16-17]都出现了许多改进和优化,例如文献[18]将CNNs的深度扩展到100层以上,进一步提升了网络学习能力.同时,网络中的数据处理也通过引入不同的规范化技术(批处理规范化[19]、层规范化[20]、实例规范化[21]、组规范化[22])调整数据分布,防止梯度爆炸,加快收敛速度.这些技术均有效改善了嵌入表示提取的效率和准确性.
在嵌入表示分类方面,采用全连接层实现回归计算后,最通用的方法是通过最小化基于Softmax函数的交叉熵损失(Softmax损失函数)来训练分类器.虽然最小化Softmax损失函数可以使学习到的预测数据分布接近训练数据的真实分布,但Softmax损失函数存在2点问题:1)对输入值的模长敏感.当嵌入表示位于决策边界附近时,随着嵌入表示或权重的模长增加,损失会越来越小,CNNs容易过早收敛[23].2)并不鼓励增大类内紧凑性和类间分离性.此时学习到的嵌入表示虽然具有可分性,但是判别性不强.针对这2个问题,已经出现了许多解决方案.中心损失函数(center loss)[24],通过加权的方式将约束类内距离的成对聚类损失函数(coupled clusters loss, CCL)与Softmax损失函数相结合,增强了嵌入表示的类内紧凑性.L-Softmax损失函数[25]引入了边距因子,并通过设计一个与该边距因子相关的乘性角度边距函数来增加正类实例学习的难度,使嵌入表示在类内更加紧凑.文献[26]将L-Softmax损失函数中的全连接层权重归一化,得到A-Softmax损失函数,并在一系列开集人脸识别任务中验证了它的有效性.AM-Softmax损失函数[27]将A-Softmax损失函数中的乘性角度边距转换为加性角度边距,通过引入尺度因子和归一化嵌入表示,进一步提升了人脸识别准确性.除了针对Softmax损失函数进行改进外,学者们还提出了基于样本对或三元组的损失函数计算方法,如对比损失函数(contrastive loss)[28]、三元组损失函数(triplet loss)[29]、多种相似性损失函数(multi-similarity loss)[30]等.但这些方法需要样本配对组合,当训练样本量巨大时,需要筛选样本,网络的性能严重依赖所选择的训练样本.实际上,triplet loss,以及基于Softmax损失函数改进的一系列损失函数大多将类内相似性sintra和类间相似性sinter集成到相似性对中,并通过最小化sinter-sintra实现优化,但这样的收敛状态不确定.针对该问题,文献[31]基于softplus框架提出圆损失函数(circle loss),该损失函数通过引入基于相似性的权重更新因子,可以分别优化sintra和sinter,改善了网络学习的收敛效果.
针对Softmax损失函数存在的问题,本文借鉴多种相似性的思想,在Softmax交叉熵损失框架下提出了一种基于余弦相似性的Softmax(cosine similarity-based Softmax, CS-Softmax)损失函数,可实现判别性更强的决策边界控制,有利于提高嵌入表示的类内紧凑性和类间分离性.同时,与circle loss,triplet loss等损失函数相比,使用CS-Softmax损失函数不需要筛选样本对,复杂度较低.在典型的音频和图像数据集上的实验结果也表明,使用CS-Softmax损失函数可以有效提升分类效果.
1 Softmax损失函数
采用Softmax损失函数的CNNs分类框架如图1所示.设一个包含C类实例的分类任务,若某个实例的嵌入表示为x,它属于第j类的概率可以用Softmax函数评估:
(1)
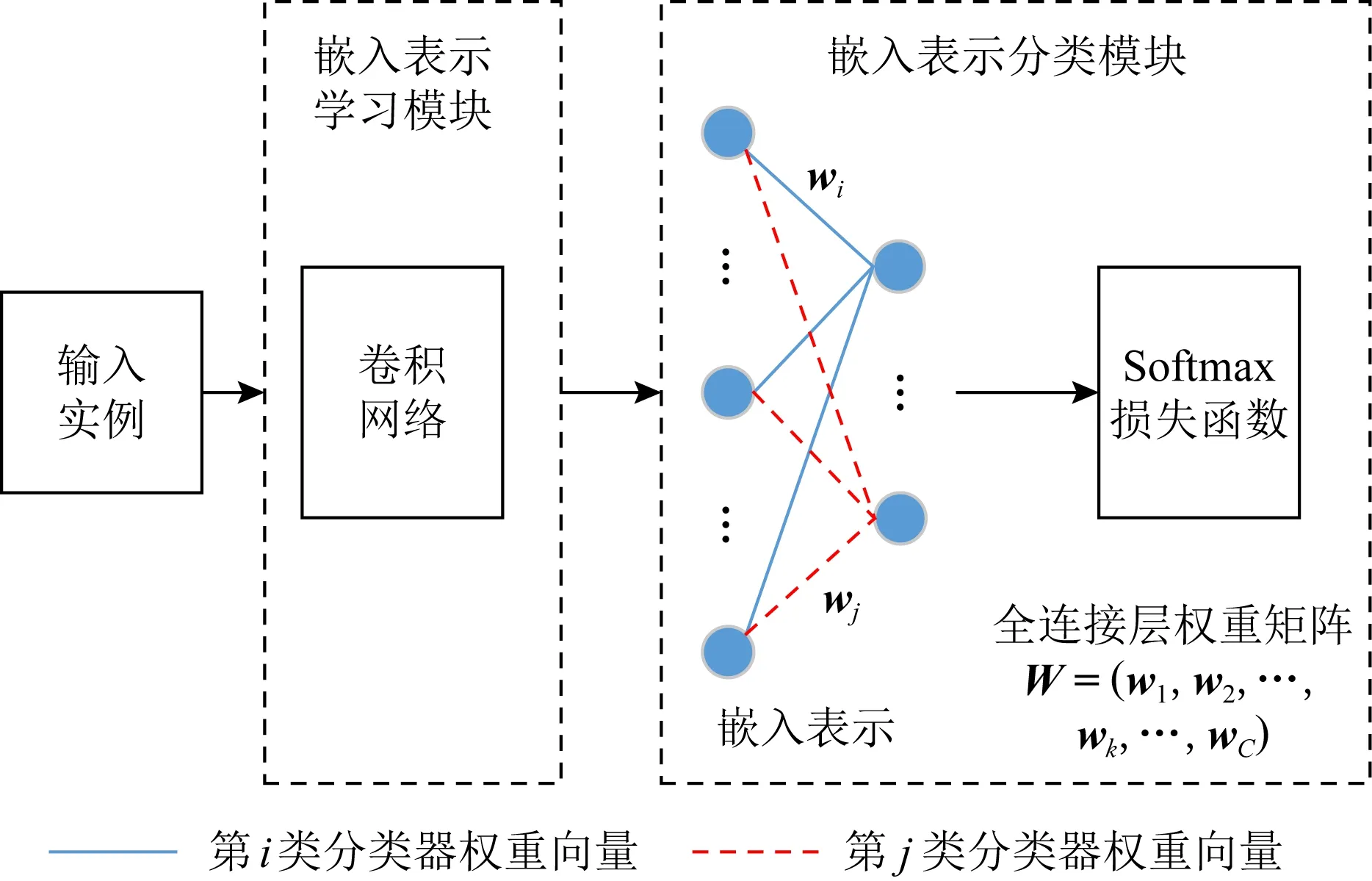
Fig. 1 Classification framework using CNNs and Softmax loss图1 使用CNNs和Softmax损失函数的分类框架
若x属于第i类,则对应的Softmax损失函数表示为
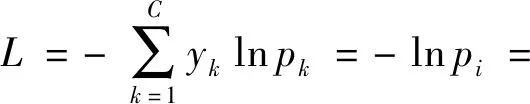
(2)

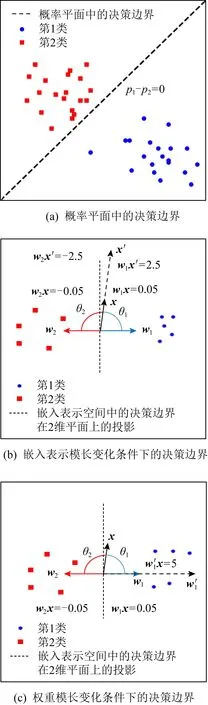
Fig. 2 Decision boundaries of Softmax loss function under binary classification图2 在二分类任务中Softmax损失函数的决策边界
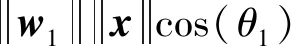
2 CS-Softmax损失函数
2.1 正负余弦相似性
在全连接层中,将各输出节点的偏置设为0,对嵌入表示x和权重进行归一化(如图3所示),将输出转换为x与全连接层权重的余弦相似性向量S=(s1,s2,…,sk,…,sC).其中,sk为
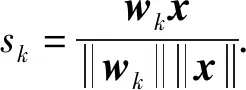
(3)
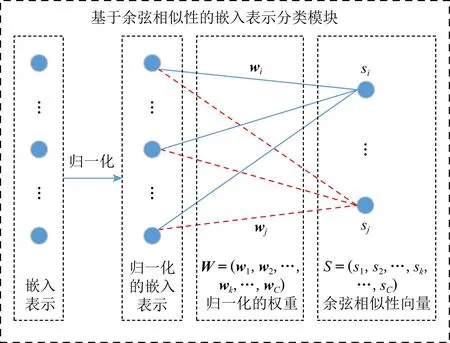
Fig. 3 Classification module of embedding based on cosine-similarity图3 基于余弦相似性的嵌入表示分类模块
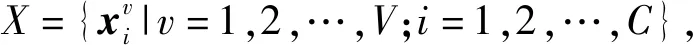
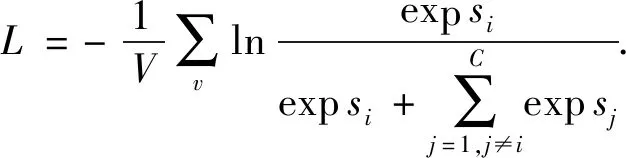
(4)
2.2 CS-Softmax损失函数的推导
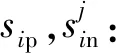
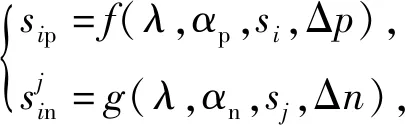
(5)
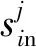
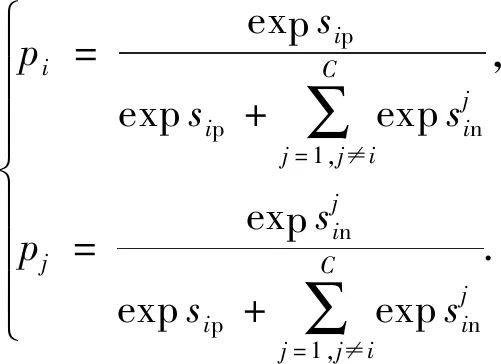
(6)
该实例对应的CS-Softmax损失函数为
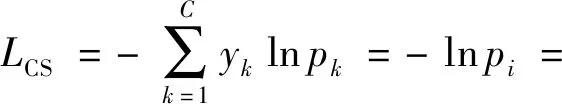
(7)
进一步地,对于嵌入表示集合X,平均CS-Softmax损失函数值估计为
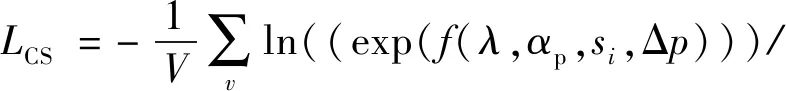
(8)
本文采用基本的线性更新公式来实现f()和g():
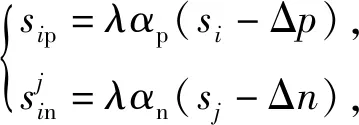
(9)
此时的CS-Softmax损失函数为
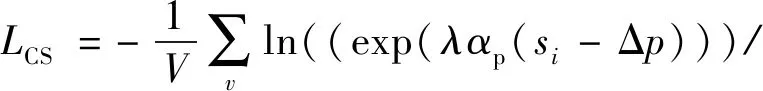
(10)
观察可知,当αp=αn=1,Δn=0时,此时的CS-Softmax损失函数就退化成了AM-Softmax损失函数:
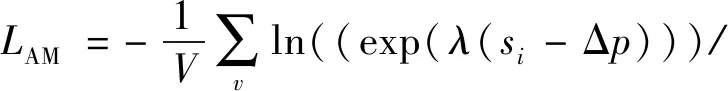
(11)
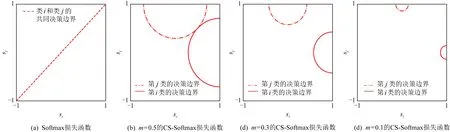
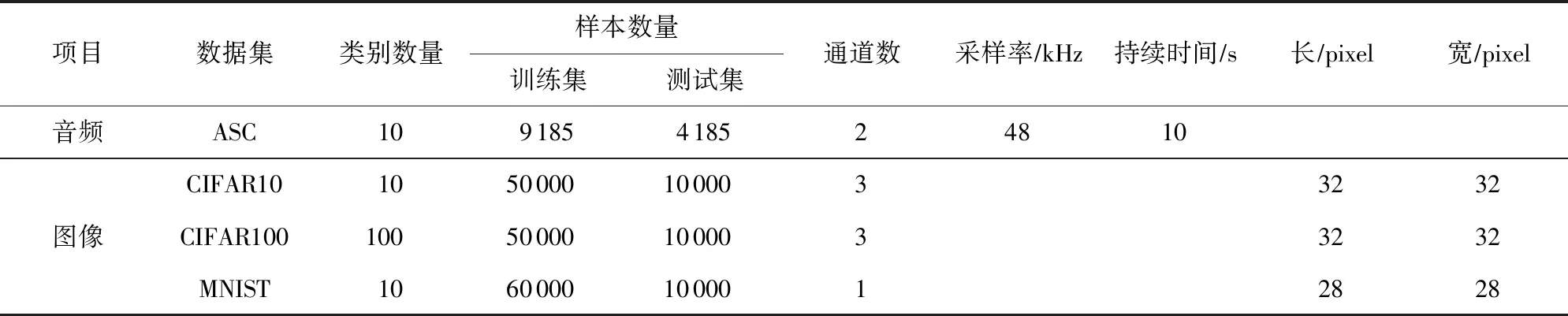
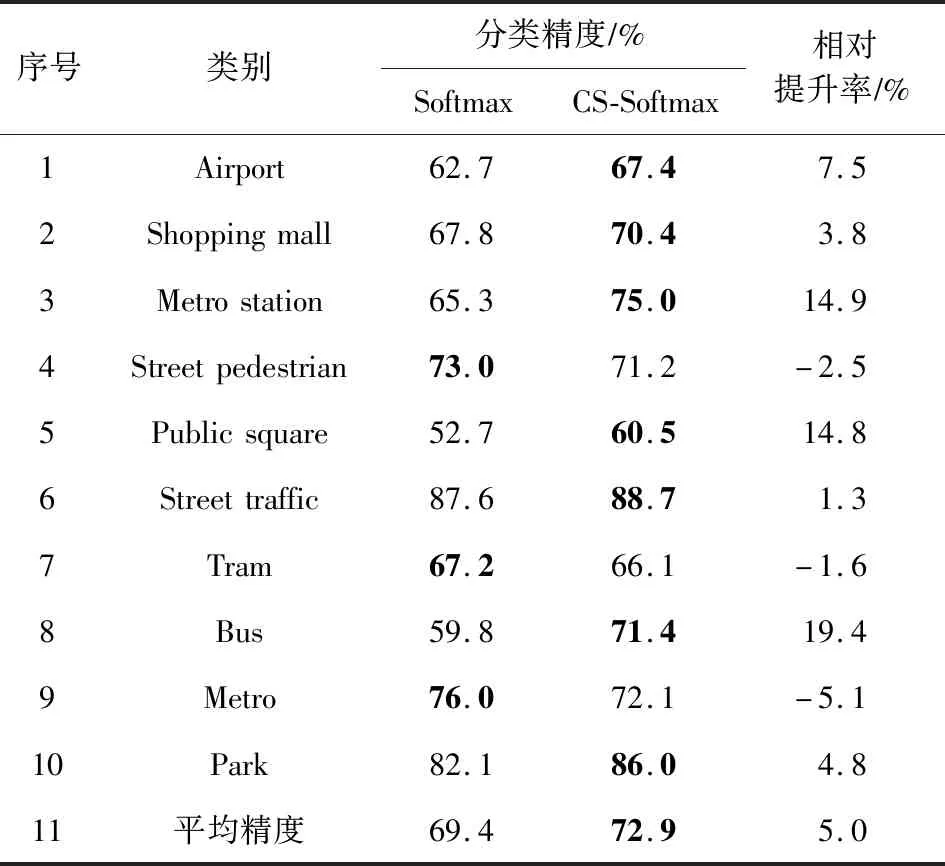
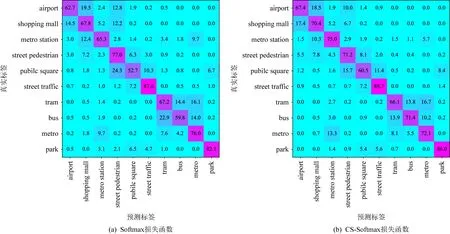
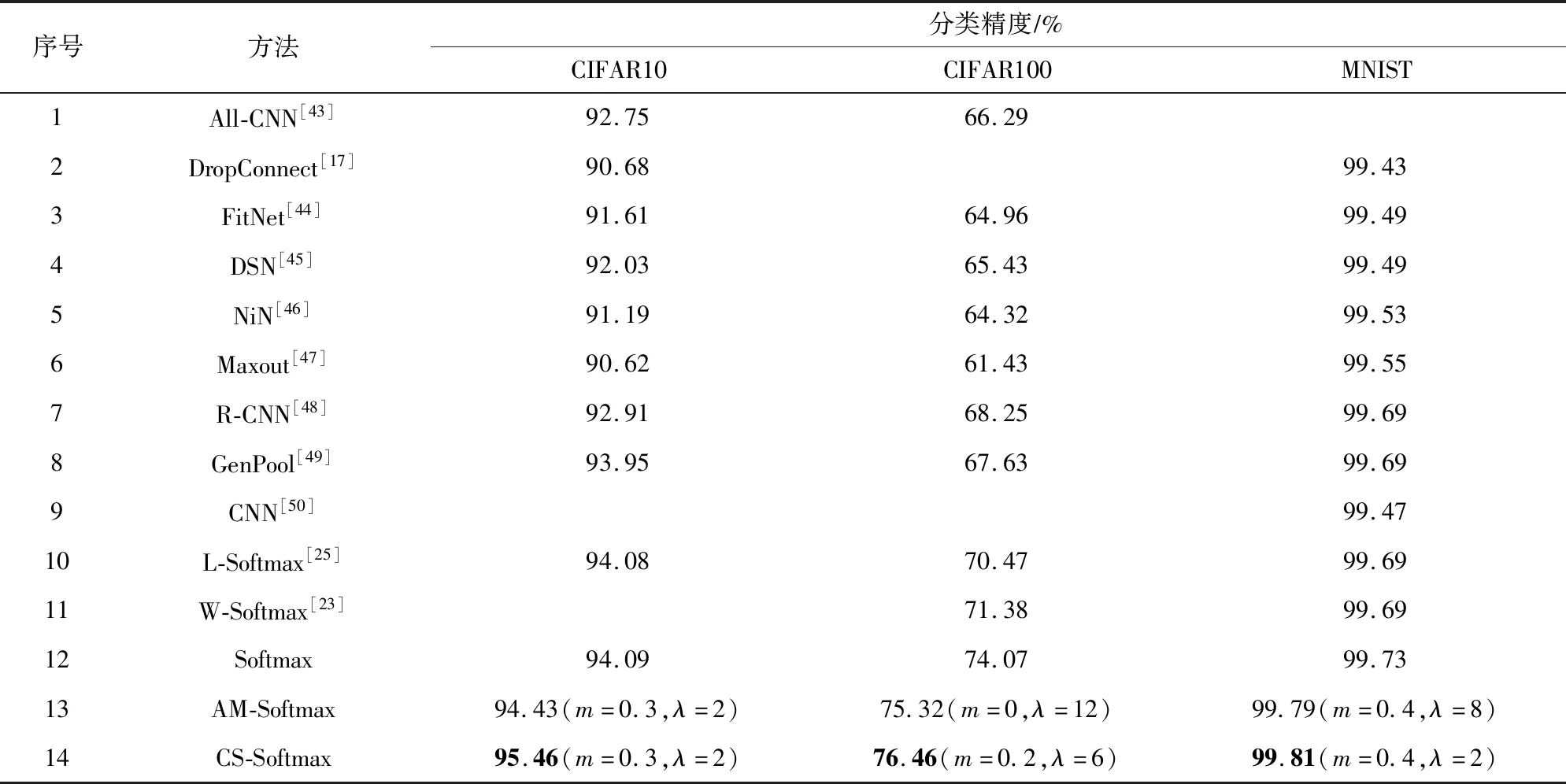
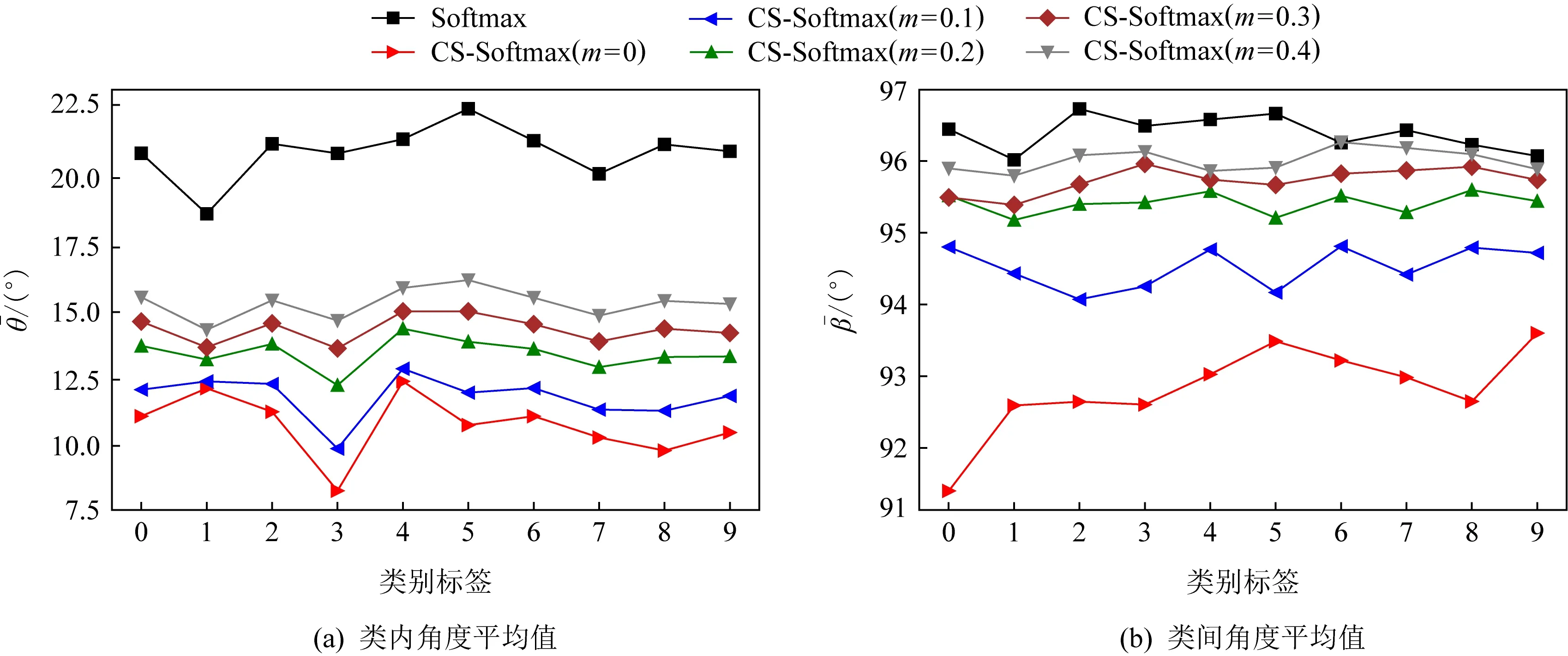
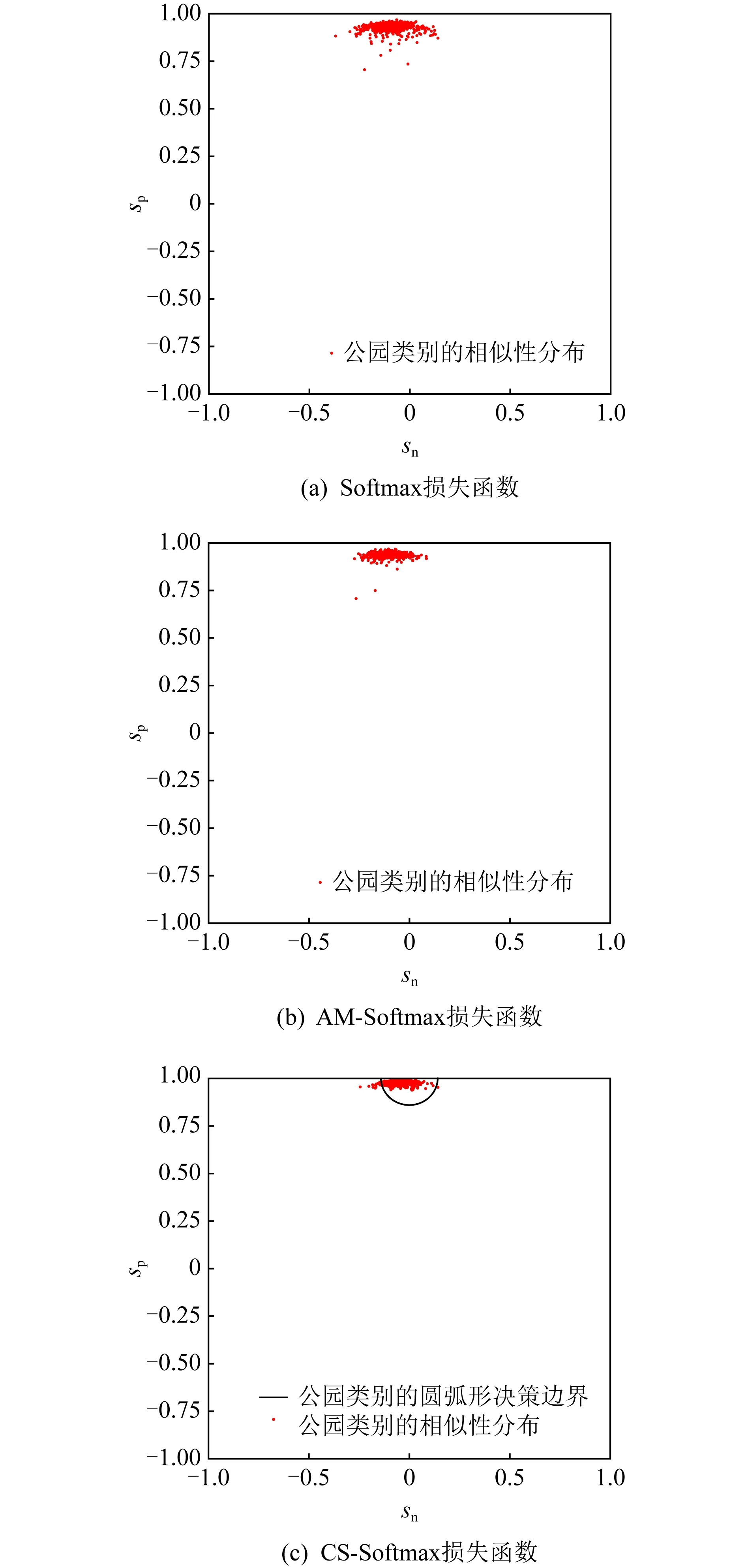
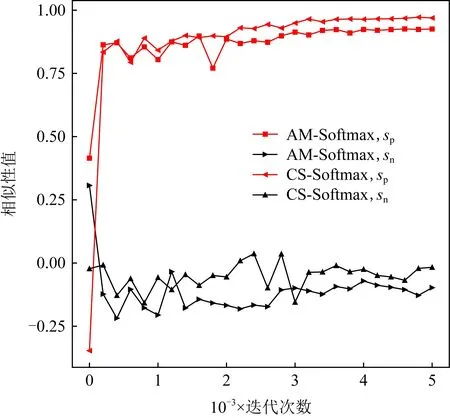
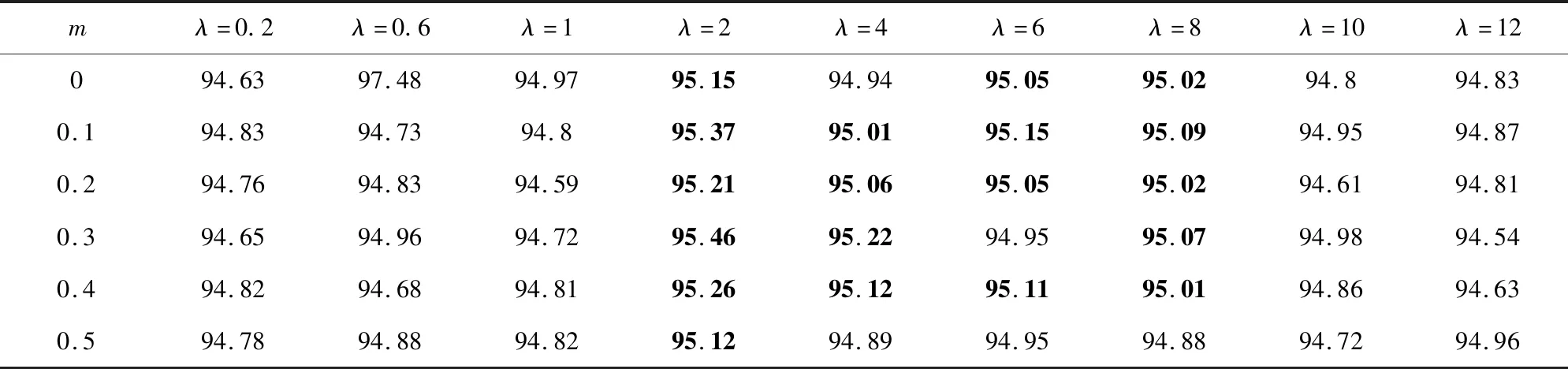
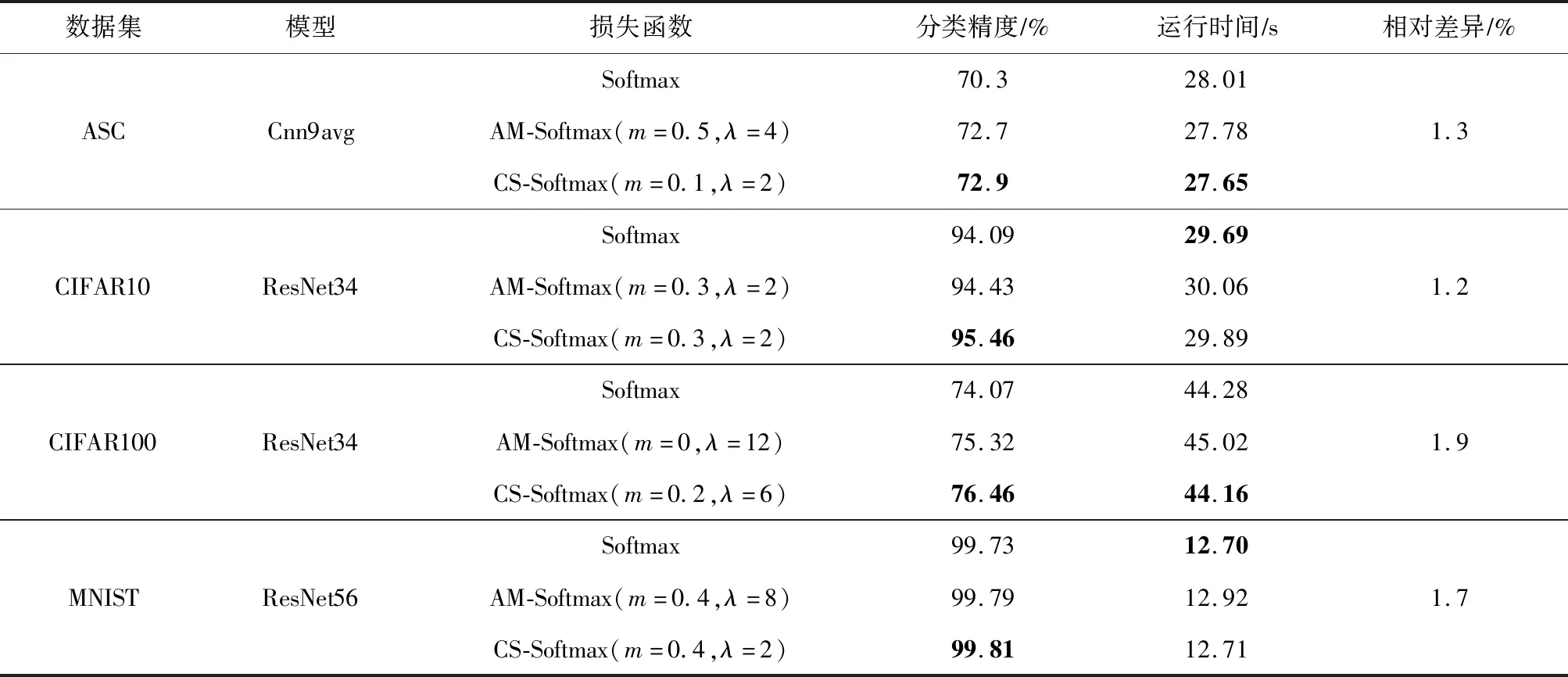
正相似性si反映同类样本间的相似性,因此越大越好.同理,负相似性sj应越小越好.因此,为有效区分正、负相似性,可分别设正相似性的训练目标op>si和负相似性的训练目标on (12) 这样,当si接近op、sj接近on时,相应的权重更新因子能够动态减小,优化过程更平缓. 将式(12)代入式(9),可以得到: (13) (14) (15) 因此,op=2-Δp,on=-Δn,Δp=1-Δn.不失一般性,可设Δn=m(0≤m≤1),则Δp=1-m,on=-m,op=1+m.此时,简化后的正、负相似性度量为 (16) CS -Softmax损失函数为 (17) 训练时,利用CS -Softmax损失函数分别最大化si、最小化sj.测试时,使用原始的余弦相似性向量S计算Softmax逻辑值进行预测.对比式(2)、式(17)可知,Softmax与CS -Softmax损失函数的唯一差别是用于Softmax函数计算的逻辑值不同:Softmax损失函数直接使用全连接层输出的内积作为逻辑值,而CS -Softmax损失函数使用的逻辑值是关于内积的二次多项式,并未增加计算复杂度.所以CS -Softmax与Softmax损失函数的时间复杂度属于同一个量级.同理,对比式(11)、式(17)可知,CS -Softmax与AM-Softmax损失函数的时间复杂度也属于同一个量级.因此使用CS -Softmax损失函数训练网络不会增加额外的时间成本.第3节的时间复杂度对比分析实验也验证了这一点. 将式(15)所得的参数代入式(14)可得类i与类j之间相似性区分的决策边界为 (18) 同理可得类j与类i之间相似性区分的决策边界为 (19) 图4绘出了CNNs分类框架中Softmax损失函数和CS -Softmax损失函数对应的二分类决策边界.可以看出,Softmax损失函数对应的决策边距是0,而在CS -Softmax损失函数中,2个类之间存在2个决策边界,间距与m相关.由式(18)、式(19)可以推出,在判定实例属于类i和类j的决策边界上,余弦相似性分别满足si-sj≥1-2m和si-sj≤-(1-2m).因此2个类的决策边界间距至少为2(1-2m),并且只要m≤0.5,2个类的决策边界就不会相交.对比图4(b)~(d)可以发现,当m由0.5变为0.1时,类i与类j之间的决策边距逐渐增加,即正负相似性之间的差值越来越大,这将使学习到的嵌入表示对应的正相似性不断接近1,负相似性不断接近0,即类内方差越来越小,类间方差越来越大,从而实现类内更加紧凑、类间更加远离.在测试阶段,使用原始余弦相似性向量S进行预测,2个类的决策边界是一致的,为si-sj=0.如果训练时类i的实例被正确分类,那么si-sj≥2(1-2m)>0,则在测试阶段,该实例也能至少以边距2(1-2m)被正确分类. Fig. 4 Decision boundaries of category i and j when the classification module outputs the cosine similarity图4 在分类模块输出余弦相似性的情况下类i和类j之间的决策边界 为了评估CS -Softmax损失函数的性能,选取典型的音频和图像数据集(声学场景分类(acoustic scene classification, ASC)[33]、MNIST[12]、CIFAR10/100[34])进行仿真实验.实验中,选用Softmax损失函数和AM-Softmax损失函数[27]作为对比方法.AM-Softmax损失函数集成了尺度因子和正相似性边距因子这2类参数,含义与CS-Softmax损失函数中的对应参数类似.为了公平对比,如果损失函数存在可调整的超参数,均选取获得最佳性能的参数组合.实验性能评估采用通用的分类精度评估标准[35].所有实验在配备NVIDIA 2080Ti GPU的工作站上实现. 实验中采用的音频和图像数据集详细信息如表1所示: Table 1 Typical Acoustic and Image Datasets表1 典型的音频和图像数据集 1) ASC.使用2019年声学场景和事件检测与分类竞赛中的ASC开发数据集进行实验.实验中,将每个实例数据转换为单通道,降采样至32 kHz,计算对数梅尔谱能量特征,特征形状为640×64,其中640是帧数,64是梅尔频率数.分别采用Cnn5avg,Cnn9avg,Cnn13avg,Cnn9max模型作为网络结构[36].在这4个网络结构中,采用相同的实验设置:激活函数为ReLU[14],批大小为32.所有特征采用训练集特征的均值和方差进行归一化处理.训练持续5 000次迭代,使用Adam优化器[37],初始学习率设置为0.001,每隔200次迭代,衰减为原来的0.9倍.网络中使用权重初始化[15]和批标准化[19]. 2) CIFAR10/100.实验中,2个数据集均采用ResNet34[18]作为网络结构.其中,CIFAR10采用随机水平翻转和不改变图像尺寸的随机裁剪增强训练样本.所有实例使用训练集的均值和方差进行归一化处理.CIFAR10训练持续6.4万次迭代,初始学习率设置为0.1,在第3.2万、4.8万次迭代时,依次衰减为0.01,0.001.批大小设置为128.CIFAR100训练持续200轮,初始学习率设置为0.1,在第60,120,160轮时依次衰减50%.2个任务的网络都使用SGD优化器[38].批大小设置为256. 3) MNIST.实验采用ResNet56[18]作为网络结构.所有实例使用训练集的均值和方差进行归一化处理.训练持续200轮,使用SGD优化器[38],初始学习率设置为0.1,在第100,150轮时依次衰减90%.批大小设置为256. 1) ASC的实验结果.表2给出了在不同网络结构上,CS-Softmax等损失函数的分类性能及对应超参数设置.其中每个网络结构中最好的结果用黑体表示,对应的参数设置在括号中说明.Softmax损失函数对应的结果来自文献[36].从表2可以看出,当采用Cnn13avg网络模型,m=0.5,λ=4时,CS -Softmax损失函数对应的精度为68.0%,比AM-Softmax损失函数高1.1%,比Softmax损失函数高6.6%.在所有对比的网络模型中,CS -Softmax损失函数性能均超过了其他损失函数. Table 2 Classification Accuracies of Three Loss Functions on Four Network Structures on ASC Dataset表2 在ASC数据集上3种损失函数在4种网络结构上的分类精度 表3综合对比了在ASC数据集上采用不同CNNs框架和损失函数的分类结果.所有方法均使用对数梅尔谱能量特征作为输入.其中,前3行均是单模型使用Softmax损失函数进行训练得到的分类精度,行2采用了注意力机制.行4是基于二值交叉熵损失函数,使用多层感知机对3个卷积神经网络进行融合训练对应的分类精度.最后3行是在Cnn9avg网络中,分别采用3种损失函数训练取得的分类结果.其中,Softmax损失函数的准确率是69.4%,这是我们使用文献[36]提供的框架获得的最好结果.虽然这个结果比原文中的准确率70.3%低,但是差别在1%之内,复现结果可信.从表3中可以看出,CS -Softmax损失函数将Cnn9avg网络结构对应的分类精度由69.4%提升至72.9%,性能优于其他分类方法. Table 3 Classification Accuracies of Different Schemes on ASC Dataset 表4进一步给出了使用CS -Softmax损失函数和Softmax损失函数训练Cnn9avg模型得到的ASC的详细分类精度.图5对比了2种损失函数的分类混淆矩阵.从图5(a)中可以看出,公共汽车(bus)误判为有轨电车(tram)、公共广场(public square)误判为街头道路(street pedestrian)的比例分别为22.9%,24.3%,说明这2对类别之间相似性较大,容易误判.由表4可知,采用CS -Softmax损失函数时,虽然有轨电车等3类场景的分类准确率出现小幅度下降,但公共汽车、公共广场的分类准确率大幅提升(幅度分别为19.4%,14.8%).公共汽车和有轨电车、公共广场和街头道路这2对相似场景的误分类比例显著降低.以上结果表明:利用CS -Softmax损失函数训练网络,原本相似类别之间的差异变大,整体分类性能得到提高. Table 4 Classification Accuracies of Two Loss Functions on ASC Dataset 2) CIFAR10/100,MNIST的实验结果.表5综合对比了在CIFAR10/100,MNIST数据集上不同分类方法的结果.前9行分别是使用Softmax损失函数训练不同的网络结构得到的分类精度.行10和行11是采用CNNs框架,分别使用L-Softmax[25]和W-Softmax[23]损失函数训练得到的分类精度.最后3行是以ResNet34或ResNet56为网络结构,分别使用3种损失函数训练取得的分类结果.可以看出,不论采用何种损失函数,ResNet34或ResNet56网络结构对应的分类精度都要优于其他网络结构的结果.同时,采用CS-Softmax损失函数的方法取得了最佳分类性能.与采用相同网络结构的Softmax损失函数方法相比,在CIFAR10/100,MNIST数据集上,分类精度分别提高了1.37%,2.39%,0.08%. Fig. 5 Confusion matrix of two loss functions on ASC dataset图5 在ASC数据集上2种损失函数的混淆矩阵 序号方法分类精度∕%CIFAR10CIFAR100MNIST1All-CNN[43]92.7566.292DropConnect[17]90.6899.433FitNet[44]91.6164.9699.494DSN[45]92.0365.4399.495NiN[46]91.1964.3299.536Maxout[47]90.6261.4399.557R-CNN[48]92.9168.2599.698GenPool[49]93.9567.6399.699CNN[50]99.4710L-Softmax[25]94.0870.4799.6911W-Softmax[23]71.3899.6912Softmax94.0974.0799.7313AM-Softmax94.43(m=0.3,λ=2)75.32(m=0,λ=12)99.79(m=0.4,λ=8)14CS-Softmax95.46(m=0.3,λ=2)76.46(m=0.2,λ=6)99.81(m=0.4,λ=2) 3.3.1 类内与类间平均角度 (20) (21) 图6(a)给出了嵌入表示和相应的分类器权重的夹角平均值.可以观察到Softmax损失函数对应的夹角平均值比不同参数设置下的CS-Softmax损失函数对应的夹角平均值都更大.由于更低的夹角平均值意味着类内嵌入表示更加紧凑,这说明CS-Softmax损失函数学习到的嵌入表示的类内紧凑性优于Softmax损失函数. 图6(b)给出了训练得到的各分类器权重之间的夹角平均值.可以看出,与Softmax损失函数对应的夹角相比,不同参数设置下的CS-Softmax损失函数对应的夹角都更加接近90°.向量之间的夹角越接近90°,意味着向量之间越不相似.这说明,CS-Softmax损失函数学习到的嵌入表示的类间相似性更小,类间可分离性优于利用Softmax损失函数学习得到的嵌入表示. Fig. 6 Comparison of the average angle values learned by Softmax and CS-Softmax loss functions on MNIST dataset图6 在MNIST数据集上Softmax和CS-Softmax损失函数学习到的平均角度值比较 3.3.2 收敛性能 本节在ASC数据集上,以Cnn9avg为网络结构,对比研究了CNNs采用CS-Softmax损失函数训练时的收敛状态及收敛过程.其中,正相似性sp为公园(park)实例的嵌入表示与同类别分类器权重的余弦相似性,负相似性sn为公园实例的嵌入表示与机场(airport)类别分类器权重的余弦相似性.AM-Softmax损失函数、CS-Softmax损失函数的超参数设为表2中采用Cnn9avg网络取得最高分类精度所对应的参数. 1) 收敛状态.图7展现了分别经过3种损失函数训练之后的余弦相似性分布图.对比发现,利用CS-Softmax损失函数学习得到的嵌入表示正相似性更加接近1,负相似性更加接近0,说明学习到的嵌入表示距离所属类别分类器权重更近,可以有效避免早停问题.同时,CS-Softmax损失函数学习到的嵌入表示在(sn,sp)二维平面中更加接近点(0,1),分布更为集中,收敛状态更加明确. Fig. 7 Comparison of positive and negative similarity distributions with Cnn9avg trained with three loss functions on ASC dataset图7 在ASC数据集上使用3种损失函数训练Cnn9avg网络对应的正负相似性分布比较 2) 收敛过程.图8对比了使用CS-Softmax损失函数和AM-Softmax损失函数进行训练时的正负相似性变化曲线图.由于在高维嵌入表示空间中,随机分布的嵌入表示倾向于相互远离[32,51],因此所有的正负相似性初值都比较小.从图8可以看出,在训练初始阶段,AM-Softmax损失函数对应的sp,sn变化速率基本相同,之后sp,sn逐渐接近优化目标1和0.而使用CS-Softmax损失函数时,初始阶段sp的变化速率要大于对应的sn,而且比AM-Softmax损失函数的sp更新速率还要大.由于sp的优化主导了训练过程,训练更加侧重于嵌入表示的聚类效果.在训练中后期,sp值依然增加,但优化较为平缓,和AM-Softmax损失函数相比,CS-Softmax损失函数训练得到的嵌入表示相似性更加接近于优化目标.这从另一个方面验证了CS-Softmax损失函数的性能. Fig. 8 Change curves of positive and negative similarity values during the training process图8 训练过程中正负相似性值变化曲线 3.3.3 超参数鲁棒性 本节通过在CIFAR10数据集上的仿真实验,探究了在不同超参数设置下,使用CS-Softmax损失函数训练ResNet34模型的性能表现.表6给出了不同参数设置下的分类精度,其中黑体数字为超过95%的分类精度.从表6可以看出,无论超参数m和λ在表中如何取值,CS-Softmax损失函数取得的分类精度均高于表5中Softmax损失函数取得的分类精度.结合CS-Softmax损失函数在本文各项任务中的性能表现,一般地,m的建议取值为0.1,0.2,0.3,0.4,λ的建议取值是2,4,6,8. 3.3.4 时间复杂度 本节在典型数据集上,通过对比使用3种损失函数训练相应模型对应的平均每轮时间消耗,分析了CS-Softmax损失函数的训练时间成本.在表7中,黑体数字表示各个模型对应的最短平均每轮耗时和最高分类精度,相应的参数设置标注在括号内.其中,时间栏为训练阶段每轮的平均耗时.相对差异为最长时间、最短时间之间差值除以最长时间得到的百分比.可以看出,在所有数据集上,使用CS-Softmax损失函数训练时的平均每轮耗时,与其他2种损失函数相当,差异在2%以内.这说明,与其他2种损失函数相比,使用CS-Softmax损失函数训练网络在有效提升分类精度的同时,没有增加对应的时间成本. Table 6 Classification Accuracies of ResNet34 Trained with CS-Softmax Loss Function on CIFAR10 Dataset with Different Hyperparameters Table 7 Comparison of the Time Cost of Training the Corresponding Models on Typical Datasets Using Three Loss Functions 本文从余弦相似性的角度出发,对全连接层做出了新的解释,并分析了基于余弦相似性的损失函数可以有效减轻使用Softmax损失函数训练时CNNs的早停问题.基于余弦相似性,提出了一种CS-Softmax损失函数.应用该方法,可以通过参数m调整决策边距,使学习到的嵌入表示类内更加紧凑、类间更加远离,判别性更强,并且优化过程可有效区分不同目标,收敛状态更加确定.在典型音频、图像分类数据集上的初步实验表明,该损失函数与Softmax,AM-Softmax损失函数的训练时间成本相当.与Softmax损失函数相比,CS-Softmax损失函数能够明显提升分类性能;与最先进的损失函数相比,CS-Softmax损失函数能够获得相当或更好的分类精度. 作者贡献声明:张强进行了论文相关问题的定义、理论分析、实验设计、编码测试、论文撰写等工作;杨吉斌提出了研究思路,给予了理论分析和论文写作的指导;张雄伟指导了实验方案的设计、论文结构的修改;曹铁勇进行了实验补充设计讨论及论文修改;郑昌艳进行了部分实验测试和整理工作.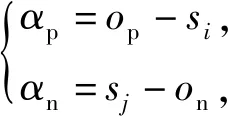
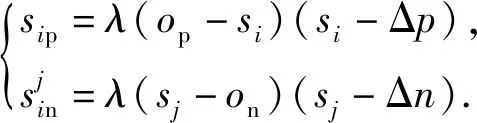
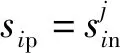
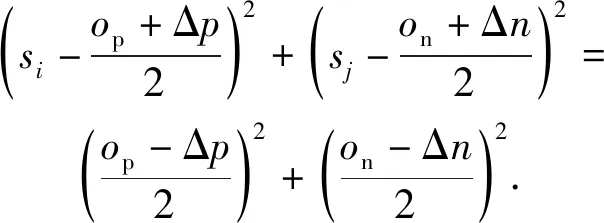
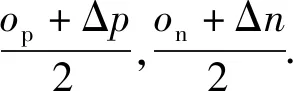
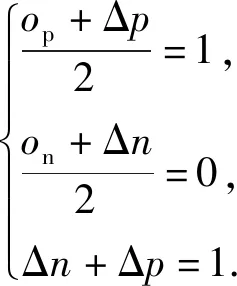
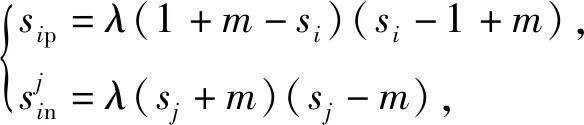
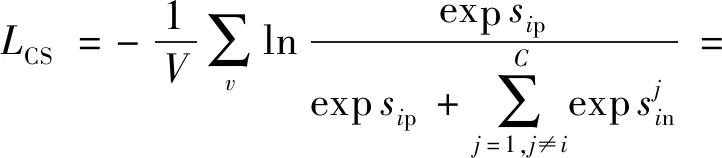
2.3 CS-Softmax损失函数的类别决策边界
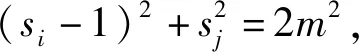
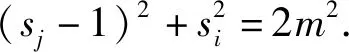
3 仿真实验和分析
3.1 数据集与实验设置
3.2 实验结果分析与讨论


3.3 CS-Softmax损失函数性能分析
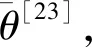
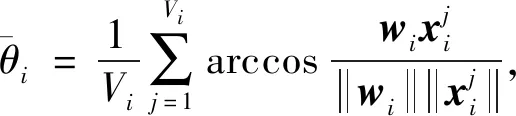
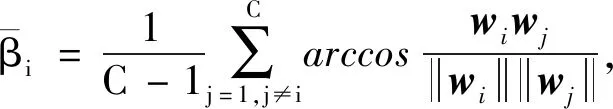
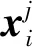
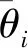
4 结 论

