固体火箭发动机喷管橡胶堵盖承压状态仿真方法研究①
张 猛,杨大望,杨 明,段佳倩,李修明
(上海航天动力技术研究所,上海 201109)
0 引言
堵盖是固体火箭发动机喷管的重要组成部分之一,对于喷管的使用寿命有重要的意义。堵盖通常采用粘接的方式固定在发动机喷管内型面上,在发动机存储、运输以及挂飞过程中起到密封防潮的作用,同时为发动机提供满足要求的点火压强。堵盖的材料主要有硬铝、纯铜等金属堵盖以及橡胶堵盖两类。陈佩风等通过试验方法,对堵盖老化性能开展研究,明确了其主要失效模式及其对喷管寿命产生的影响。王纪霞等也通过工艺等方面,就堵盖的安全性及其使用安全性对喷管乃至固体火箭的重要意义开展了相应研究。目前,也有很多学者对堵盖的作用及打开性能开展了研究,研究方法也逐渐成熟,但主要针对金属堵盖。而橡胶堵盖由橡胶和织物(夹布)两部分组成,其中橡胶是一种性能较为复杂的高分子聚合物,具有超弹性,且夹布与橡胶之间的相互作用也很难计算,目前对于橡胶堵盖的计算与校核尚无精确的方法。因此,有必要提出一种简单、快速、有效的计算方法,以提高橡胶堵盖的设计效率。
近年来,随着Abaqus、Ansys等有限元软件及相关理论的发展,有限元仿真技术的应用愈加广泛,同时随着对橡胶等超弹性材料研究的逐渐深入,学者们也提出了很多的模型,用来表征不同工况下的橡胶等超弹性材料的力学性能。在此基础上,本文提出一种基于Abaqus的橡胶堵盖仿真计算研究方法,采用常用的几种超弹性模型,对橡胶堵盖常用橡胶(5171橡胶)的性能进行研究,并对堵盖模型提出部分假设与简化,对某固体火箭发动机橡胶堵盖0.3 MPa的承压工况进行有限元仿真计算,最后通过试验,对该方法进行了验证。
1 堵盖材料性能研究
1.1 材料力学性能试验
对堵盖组成材料(5171橡胶及夹布单丝)分别开展常温拉伸试验,橡胶所用试件为照标准GB/T 528—2009中I型哑铃试件,形状及参数如图1所示。
试件测3组,试验曲线如图2所示。由图2可见,试验曲线呈现非线性,且3组试验数据相差较小。
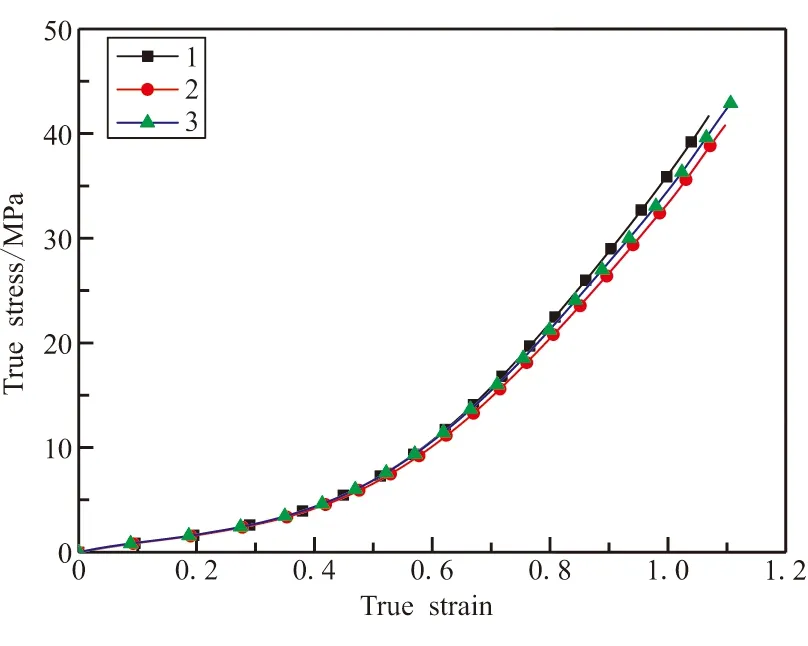
图2 橡胶真实应力-真实应变曲线Fig.2 True stress-strain curves of rubber

(a)Dumbbel rubber specimen
堵盖中除橡胶材料外,还有夹布作为增强体,其主要承载作用。因此,为提高仿真精度,获取夹布单丝材料性能,对其进行了拉伸试验,试验曲线如图3 所示,应力-应变仍呈非线性关系。
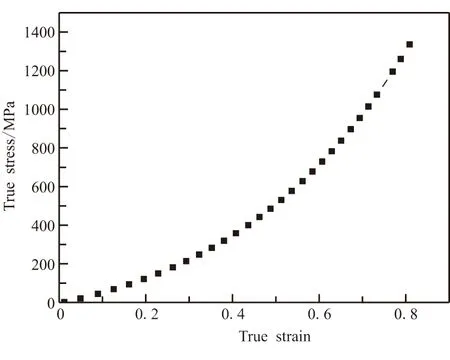
图3 夹布单丝真实应力-真实应变曲线Fig.3 True stress-strain curve of cloth thread
1.2 材料本构模型
橡胶作为一种高分子材料,其内部由大量分子链组成,如图4所示。当橡胶承受载荷作用时,其内部分子链发生蠕变,然后橡胶发生变形。因此,橡胶承受载荷作用时呈现超弹性。
图4 橡胶分子链Fig.4 Molecular chain of rubber
目前,有很多学者已对橡胶的超弹性进行了研究,并提出了大量的本构模型。较常用的有Yeoh、Ogden、Mooney-Rivlin、Neo-Hookean及Marlow等。其中,Yeoh、Ogden、Mooney-Rivlin、Neo-Hookean等模型的表达式分别为
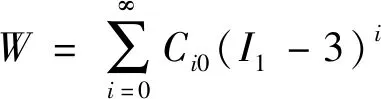
(1)
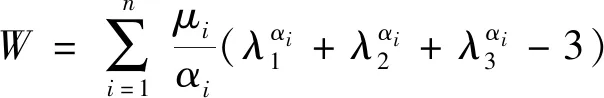
(2)
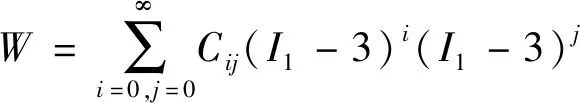
(3)
=(-3)
(4)
式中为应变能;为应变不变量;为拉伸比;、及均为模型参数,由试验数据拟合获得。
上述几种模型都是通过建立应变能与应变不变量或拉伸比之间的关系来表征橡胶材料在载荷作用下的响应。除上述几种模型外,Marlow模型是对应力与应变数据的积分来表征的,因此没有显式表达式。为提高计算精度,利用上述几种模型,分别对试验数据进行拟合,拟合情况见图5。通过拟合结果可知,选用Marlow模型,可更好地表征该橡胶的应力-应变行为。因此,选用该模型进行仿真计算。
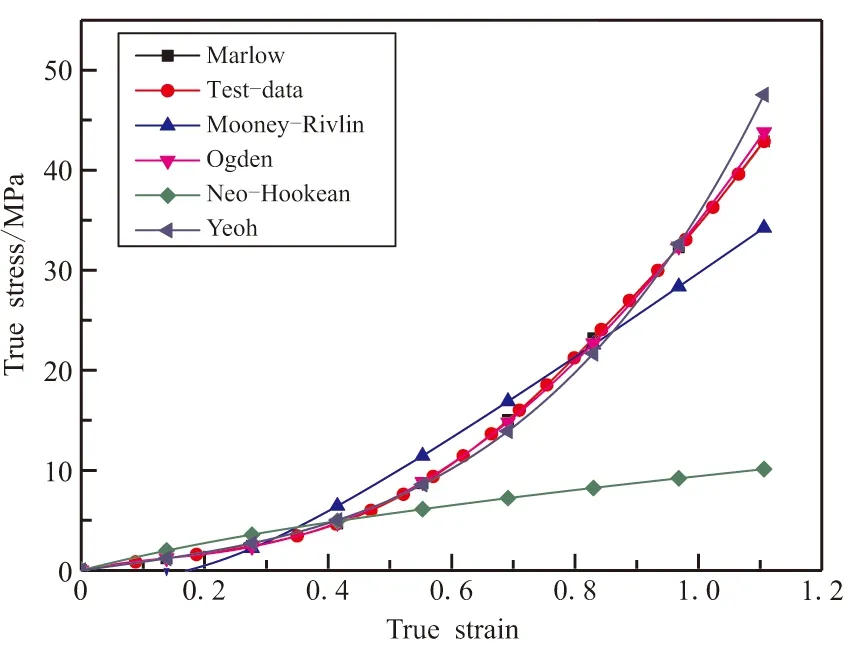
图5 各本构模型拟合情况Fig.5 Fitting of each constitutive model
堵盖中夹布起主要承载作用,由图3可知,其应力-应变亦呈现超弹性。因此,仍对其进行超弹性本构模型的拟合,如图6所示。由拟合结果可知,在丝线的整个承载过程中,采用Ogden本构模型,可更好地表征其应力-应变行为。因此,在本研究中,选取该模型对其力学行为进行表征,具体参数见表1。
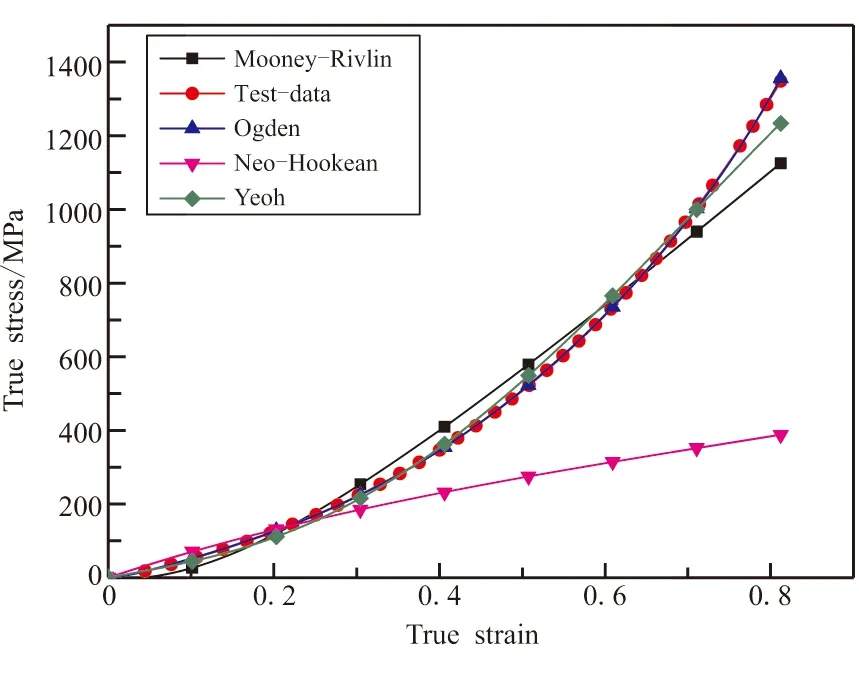
图6 夹布单丝各本构模型拟合情况Fig.6 Fitting of each constitutive model of silk with cloth

表1 Ogden本构模型参数Table 1 Parameters of ogden constitutive model
2 堵盖承压状态有限元仿真
2.1 有限元建模
某型号固体火箭发动机堵盖为一种典型的橡胶堵盖产品,采用Abaqus有限元计算软件,对其0.3 MPa设计承压状态进行仿真研究。由于橡胶堵盖是一种织物(夹布)增强橡胶复合结构,完全按照实物状态进行仿真建模较为困难。同时,根据姚远对编织布的试验研究发现,当编织布中的纱线被拉直后,编织布的力学行为与单根丝线的力学行为类似。因此,在仿真计算过程中,对原模型进行了简化:
(1)由于橡胶堵盖是对称结构,取1/2模型进行计算;
(2)将夹布简化为两层单向布,如图7所示。
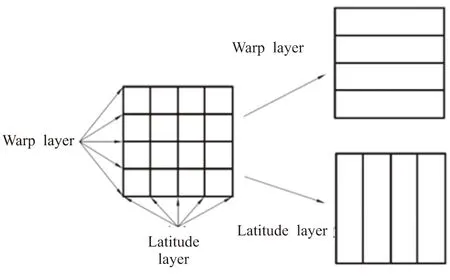
图7 夹布拆分示意图Fig.7 Schematic diagram of cloth splitting
除上述简化外,还提出以下假设:
(1)假设堵盖成型过程(硫化温度不高于150 ℃)对夹布(丝线)力学性能无影响;
(2)假设橡胶堵盖成型后丝线与附近橡胶完全粘附,承压时无相对位移;
(3)不考虑丝线之间摩擦力的影响。
基于上述简化与假设,建立有限元模型,如图8所示。建立模型后,进行有限元网格划分。其中,橡胶部分单元类型为C3D8H杂化单元,夹布用rebar单元,其具体分布角度及相关参数见表2。仿真计算时,rebar单元层通过“embeded element”命令嵌入到橡胶层之中。橡胶堵盖几何模型及网格划分情况见图9。

图9 网格划分示意图Fig.9 Mesh diagram of the nozzle closure
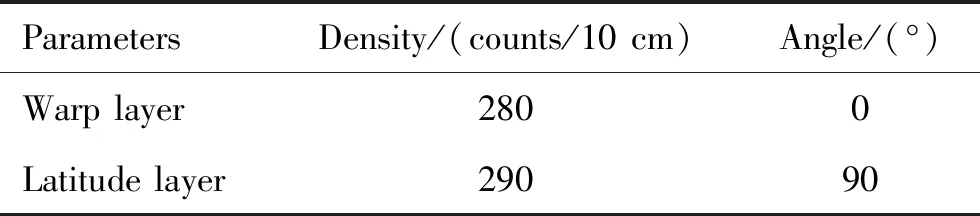
表2 夹布分布角度及相关参数Table 2 Distribution angle and related parameters of cloth
2.2 加载及边界条件
在0.3 MPa承压工况下,堵盖外圆与喉衬粘接,设置该外圆为固定边界,对称面处设为对称边界条件;内型面承受0.3 MPa均布压强,夹布层嵌入在橡胶层中。
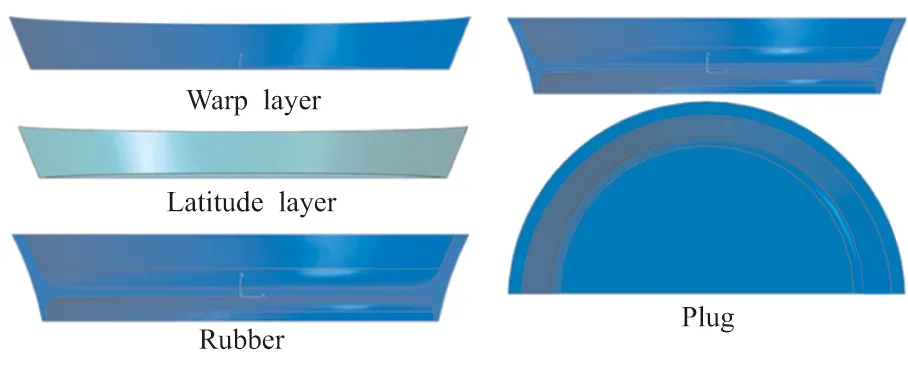
(a)Geometric model of the nozzle closure
2.3 仿真结果分析
利用上述有限元方法,对0.3 MPa承压状态的堵盖进行了仿真研究,仿真结果如图10所示。图10中,经线层和纬线层最大应力分别为70.82、70.93 MPa,远大于橡胶材料最大应力(4.76 MPa)。这是由于夹布材料轴向刚度远大于橡胶材料导致的,在该种状况下,夹布承担其中绝大部分载荷。
通过图10(a)、(b)可知,应力在丝线轴向方向从两端到中间逐渐增大,这是由材料的受力状态决定的。在垂直丝线轴向方向,从两侧到中间逐渐增大,是由于丝线只在轴向具备很高的强度,但其余方向没有承载力,且在此模型中,经、纬层丝线排布方向,相互垂直。因此,两层均呈现出载荷沿丝线轴向分布的现象,在某一层垂直丝线的力由另一层承载,此受力状态与织物受力状态基本一致,同时也表明当受压较大时,橡胶堵盖会从中间位置首先破坏,然后向四周逐渐扩展。
在0.3 MPa承压状态的力场分布如图10(c)所示。结果显示,该承压状态下,橡胶最大应力区域为内型面圆角位置,最大应力为4.76 MPa,远小于夹布层(经线层、纬线层)最大应力,这是由于其本身较软、强度较低导致的。因此,若发生橡胶撕裂等破坏,将会从受力最大(内型面圆角)的位置开始。
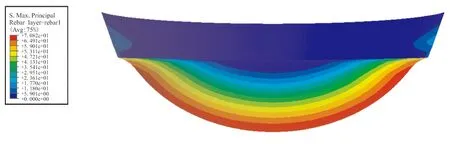
(a)Warp layer
图11为堵盖在0.3 MPa压强下位移场仿真结果。其中,两侧由于外端面与发动机结构粘接,外表面为固定端。因此,外表面位移为0。中间区域约束较少,靠材料自身性能抵抗变形。因此,其位移较大,且从四周向中心逐渐增大,堵盖中心处位移最大,为17.7 mm。
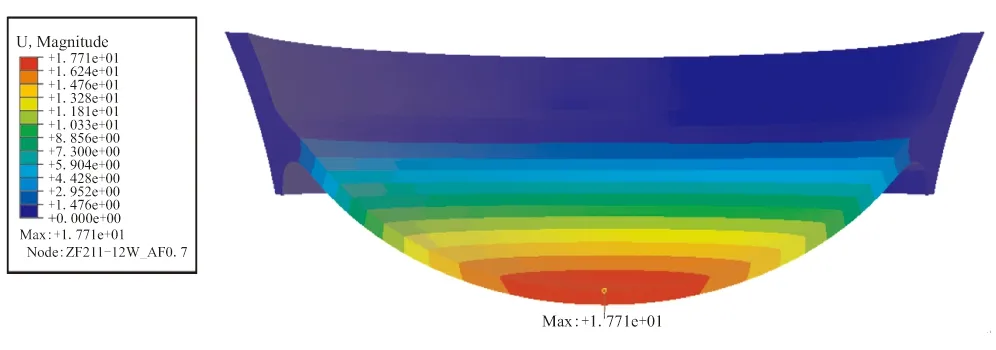
图11 0.3 MPa承压状态下堵盖位移场分布Fig.11 Displacment distribution of nozzle closure under 0.3 MPa pressure
3 试验验证
为了验证上述建模及仿真方法的有效性,本文对上述堵盖开展了0.3 MPa承压状态试验研究,受限于橡胶材料的应变测试手段不足,初步采用变形测试验证仿真结果,通过测量其中心点处的位移,以验证仿真方法的有效性。试验装置如图12所示,其中考虑到表的量程不足,初始状态时,表的探头与测量点之间距离10 mm(以标准量块确定)。所以,测量结果等于表上示数加10 mm,表显示8.313即为18.313 mm。

图12 堵盖承压试验及位移测量装置Fig.12 Pressure test and displacment measuring device for the nozzle closure
试验共进行3组,分别测量其中心点处位移分别为18.2、18.3、19.6 mm,取其平均值(18.7 mm)作为有效数据。通过数据对比可知,本文所提出的仿真方法计算所得同一位置处位移比试验低约5.3%(1 mm)。经分析,导致该误差的原因主要有:
(1)本文的仿真方法是基于2.1节所提出的假设的前提下进行的,而实际情况下,当堵盖承载时,织物丝线之间会产生相互作用,在该作用下,沿垂直丝线方向会具备一定的抗弯能力。
(2)在橡胶堵盖的成型过程中,丝线表面会涂胶并硫化,进而影响该承载力。
(3)通过对试验后的堵盖进行解剖发现,由于实际产品成型时,夹布在橡胶层中间的位置基本都会发生向下移动。在此情况下,相比于夹布完全居中时,夹布的受力会出现“延时”现象,最终会导致其位移出现偏大情况。
(4)此外,夹布还存在左右偏移情况,并未完全居中,在圆角位置出现了夹布较大的偏移接近凹陷的情况(图13),上述情况也会导致试验结果与仿真结果不一致。综合上述因素,导致堵盖在承压状态下所测量的数值出现偏大情况。

图13 试验后堵盖解剖情况Fig.13 Anatomy of the nozzle closure after the test
在上述各种影响因素的综合影响下,导致本文提出的仿真计算方法与试验对比结果产生了5.3%的误差(小于10%),认为本文提出的仿真模型与方法可用于橡胶堵盖承压状态仿真计算。
4 结论
通过橡胶堵盖承压状态仿真计算方法,研究获得了橡胶堵盖用橡胶及夹布材料在准静态拉伸载荷下的应力-应变的演化过程,得到了其相应本构模型。基于此,提出一种简化建模方法,对承压状态的受力状态进行仿真计算及试验验证。试验及仿真计算结果表明:
(1)橡胶堵盖用橡胶及夹布材料均呈现超弹特性,但对于不同材料及试验件,应根据其测试数据及应力-应变特征,选择相适用的本构模型进行表征。
(2)仿真结果与试验结果误差较小,说明编织布分离的仿真建模方法可用于指导固体火箭发动机用橡胶堵盖的设计、分析及优化,有效地避免了编织结构建模的复杂性,可有效地提高橡胶堵盖的设计效率。
(3)根据堵盖各组成结构的应力场的分布及最大应力的位置,确定了橡胶堵盖打开时的破坏模式,即从中间向四周扩展,且当堵盖设计不合理时,橡胶材料可能会从根部首先开裂,对堵盖的密封性能产生一定威胁。
(4)此建模方法为后续对橡胶堵盖的打开及橡胶堵盖破坏过程的演化规律研究奠定了坚实的基础。

