基于流动扩散互竟关系的基质吸附态瓦斯表观扩散系数实验室测定准确性分析
赵 伟,王 凯,李成武,鞠 杨,刘晨熙,魏诚敏,袁廷璐
(1.中国矿业大学(北京) 共伴生能源精准开采北京市重点实验室,北京 100083;2. 中国矿业大学(北京) 应急管理与安全工程学院,北京 100083;3. 中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083)
扩散系数是描述煤中瓦斯运移特性的关键参数,其对煤层气储量计算、瓦斯灾害危险评价以及温室气体排放估算等有着重要的意义。煤是由基质和裂隙组成的双重孔隙介质,在原始应力环境中瓦斯分别在2个系统中以扩散和流动2种形式运移。在基质中,扩散以表面扩散、诺森扩散、过渡扩散和菲克扩散为主,其通常在尺度较小的孔隙中发生,以吸附瓦斯形成的浓度梯度为主要驱动力进行传质;而裂隙尺度空间较大,传质行为较扩散更为连续、剧烈,根据雷诺数的大小,流动又可分为层流、过渡流和紊流。为了描述方便,原位煤层裂隙中的瓦斯流动可简单假设为符合达西方程的渗流(层流),其以游离瓦斯形成的压力梯度为主要驱动力进行运移。游离瓦斯和吸附瓦斯时刻处于动态平衡之中,两者难以区分。
扩散现象本质上是由分子化学势的不均而引起的,故而引起化学势分布不均的因素均可以引起扩散行为的变化。一般而言,影响扩散的因素可分为2类:一类决定了瓦斯的赋存状态,即扩散源浓度的大小,如压力、含量、温度和水分等因素;另一类则决定了瓦斯扩散路径的难易程度,如煤的孔隙结构、粒径和变质程度等因素。扩散是一种复杂的传质现象,因此扩散系数也存在较多分类。文献[1]中对扩散系数的分类有多种方法,以多孔介质复杂孔隙系统与单个均质孔道中瓦斯分子运移的差异性为分类依据,扩散系数可分为本质扩散系数、有效扩散系数和表观扩散系数3类。本质扩散系数为气体分子本身的扩散系数,与温度等影响分子动能的特性有关,而与扩散路径等外在因素无关。有效扩散系数是气体分子经过多孔介质蜿蜒曲折的孔道所产生的扩散系数,其与多孔介质的曲折度、孔隙率和孔长等孔隙性质有关。表观扩散系数则是大量分子在多孔介质中运移所产生的扩散系数,其不仅能反应单个分子的扩散特征,还从整体上考虑了大量分子与孔壁的相互作用以及分子与分子之间的相互作用。其不单单反应了扩散行为,也反应了流动对扩散的边界影响。一般而言,通过解吸曲线反演得出的扩散系数,其融合了流动和扩散2种典型的传质形式,其中又可细分为非线性紊流、线性层流(渗流)、菲克扩散、过渡扩散、诺森扩散以及表面扩散等多种传质形式,是一种表征宏观传质特征的表观扩散系数。
研究不同因素对煤中瓦斯扩散的影响机制时,常常通过改变常规解吸试验的某一自变量,得到表观扩散系数与其的关系曲线,进而进行分析。在实验室吸附瓦斯表观扩散系数测定方法中,通常以常规的解吸试验为基础,通过释放游离瓦斯,测算解吸瓦斯曲线,进而得到解吸分数曲线,从而推算基质中吸附态瓦斯的表观扩散系数。然而,在释放游离瓦斯过程中,由于损失时间难以把握,游离瓦斯的不同排放时间长短对解吸曲线及扩散模型拟合产生很大的影响,常会得到不同的表观扩散系数。另外,在现场测量钻屑解吸指标时,由于是煤屑第1 min的瓦斯解吸量,其与表观扩散系数存在一定的定量关系,也常因为钻屑收取过程中损失时间的差异,测出的存在较大误差。因此,有必要探究不同解吸损失时间下表观扩散系数的变化规律,来修正表观扩散系数测定的精确度。
笔者将游离瓦斯的排放时间定义为解吸损失时间,通过对游离瓦斯和吸附瓦斯的运移特征差异进行分析,构建引入游离瓦斯组分贡献的瓦斯全浓度表观扩散模型,进而分析损失时间对表观扩散系数测量准确性的影响,并基于自主研发的瓦斯解吸特性自动检测仪,试验模拟测算不同解吸损失时间下的瓦斯解吸曲线和扩散分数曲线形态,得到表观扩散系数有效值与损失时间的定量关系,从而指导精准化瓦斯表观扩散系数测定。
1 试 验
1.1 试验样品
试验煤样取自内蒙古鄂尔多斯煤田神东集团柳塔矿2煤层,属于中低变质程度烟煤,其相关物性参数见表1。

表1 煤样基本参数
1.2 解吸试验
本次解吸试验采用自主研发的瓦斯解吸特性自动监测仪(图1)。与常规通过量筒人工读数相比较,该设备具有自动化、连续化和精准化数据读取的优点。尤其对于解吸初期的解吸数据,避免了常规方法中由于短时间内大量游离瓦斯逸散,导致气泡大量生成,引起人工读数误差的问题(图2)。解吸试验在0.5,1,1.5 MPa的不同平衡压力条件下进行,得到0,1,5,10 min不同损失时间条件下的解吸曲线。具体试验步骤如下:① 首先将现场取得的煤样放入专用破碎机中破碎,之后用实验筛进行筛分。取得煤粒大小在60~80目(0.178~0.250 mm)的煤样。② 将试验煤样装入清洁的动态测压仪器中,进行真空脱气。③ 由于实验室安全要求,瓦斯以CO代替。脱气8 h左右后向煤样罐中充入CO,充至一定压力后关闭阀门,然后进行吸附平衡试验。④ 待吸附平衡后,连接解吸量自动监测仪,该仪器可每秒读取1次解吸数据。采用计算机监测不同解吸时间的解吸体积,得出解吸曲线。重复上述试验,测定不同压力下的解吸曲线。⑤ 通过Matlab编程语言,对解吸曲线进行扩散模型拟合并得出表观扩散系数。

图1 自动解吸测定装置
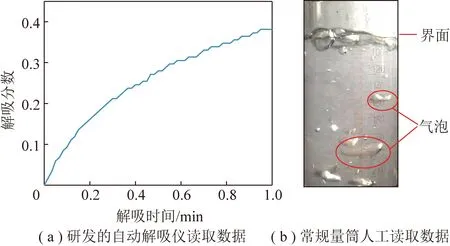
图2 不同测试方法解吸初期数据对比示意
2 结果与分析
2.1 不同损失时间条件下的瓦斯解吸特性
不同损失时间条件下的瓦斯解吸特性是分析其扩散特性变化的基础。为了避免逸散时间人工控制的误差,在试验时不同损失时间的解吸曲线通过截取特定时间段的解吸曲线形成。从图3的试验结果可以看出:和以往文献中的试验现象相似,平衡压力越大,则固定时间段内的瓦斯解吸量就越大,且瓦斯初期解吸速度越快;而随着时间推移,瓦斯解吸速度减少得也越快。而随着损失时间的增加,解吸曲线的形态会发生显著变化:曲线逐步远离轴,并靠近轴,初期“直线”解吸段的长度越来越短,瓦斯解吸速度减小的幅度越来越小。曲线形态的变化,意味着控制曲线的基本传质形式有所改变,有必要对其内部的主控传质形式进行研究。

图3 不同损失时间下的解吸曲线形态变化
2.2 不同损失时间条件下的瓦斯表观扩散系数


(1)
式中,为时刻的解吸量,mL;为极限解吸量,mL;/为解吸分数;为项数。
式(1)中等式左边时刻解吸量与极限解吸量的比值定义为解吸分数。在得到解吸曲线之后,采用渐进曲线法,依照曲线形态作解吸曲线的渐近线,取得极限解吸量,取时刻解吸量与之相除,最终得到该特定曲线的解吸分数。之后通过利用式(1)进行拟合,便可以得到不同损失时间条件下的表观扩散系数有效值。从图4和表2的拟合结果可以看出,试验煤样的表观扩散系数有效值在10~10s。而如果假设扩散距离为煤粒本身半径(0.1 mm左右),则求得的有效扩散系数在10~10m/s,和以往文献中试验测得的有效扩散系数数量级相近。而对于单孔模型的拟合度,会发现采用单孔模型拟合解吸分数曲线时拟合度不一。在损失时间为1 min时的拟合度最高,随着损失时间向两边偏离于1 min时,越偏离拟合度越差。这主要与单孔模型本身浓度恒定的假设有关。在解吸初期游离瓦斯的强烈流动影响了表观扩散系数有效值的大小,使得表观浓度波动过大;而在解吸后期,随着浓度急剧下降,且基质产生解吸收缩,孔隙结构发生了显著改变,这又与单孔模型的均质假设相悖,故形成了1 min时拟合度最高的结果。
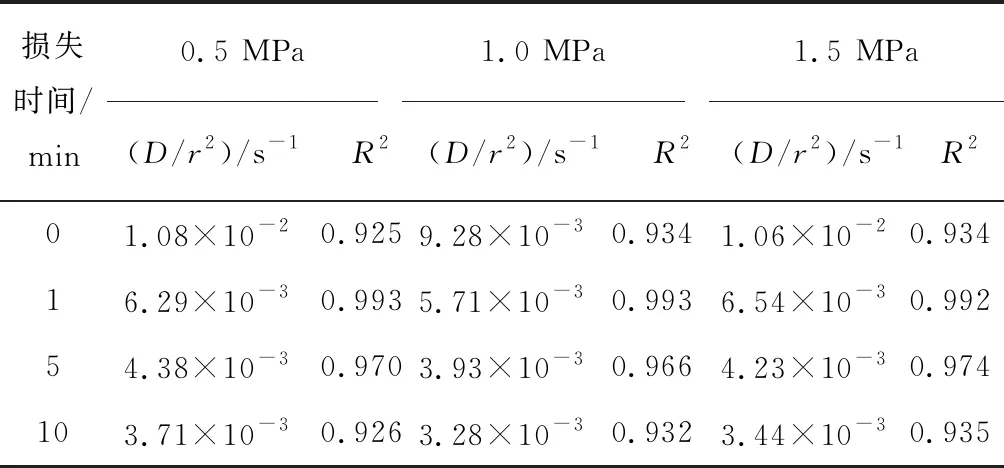
表2 表观扩散系数有效值拟合结果
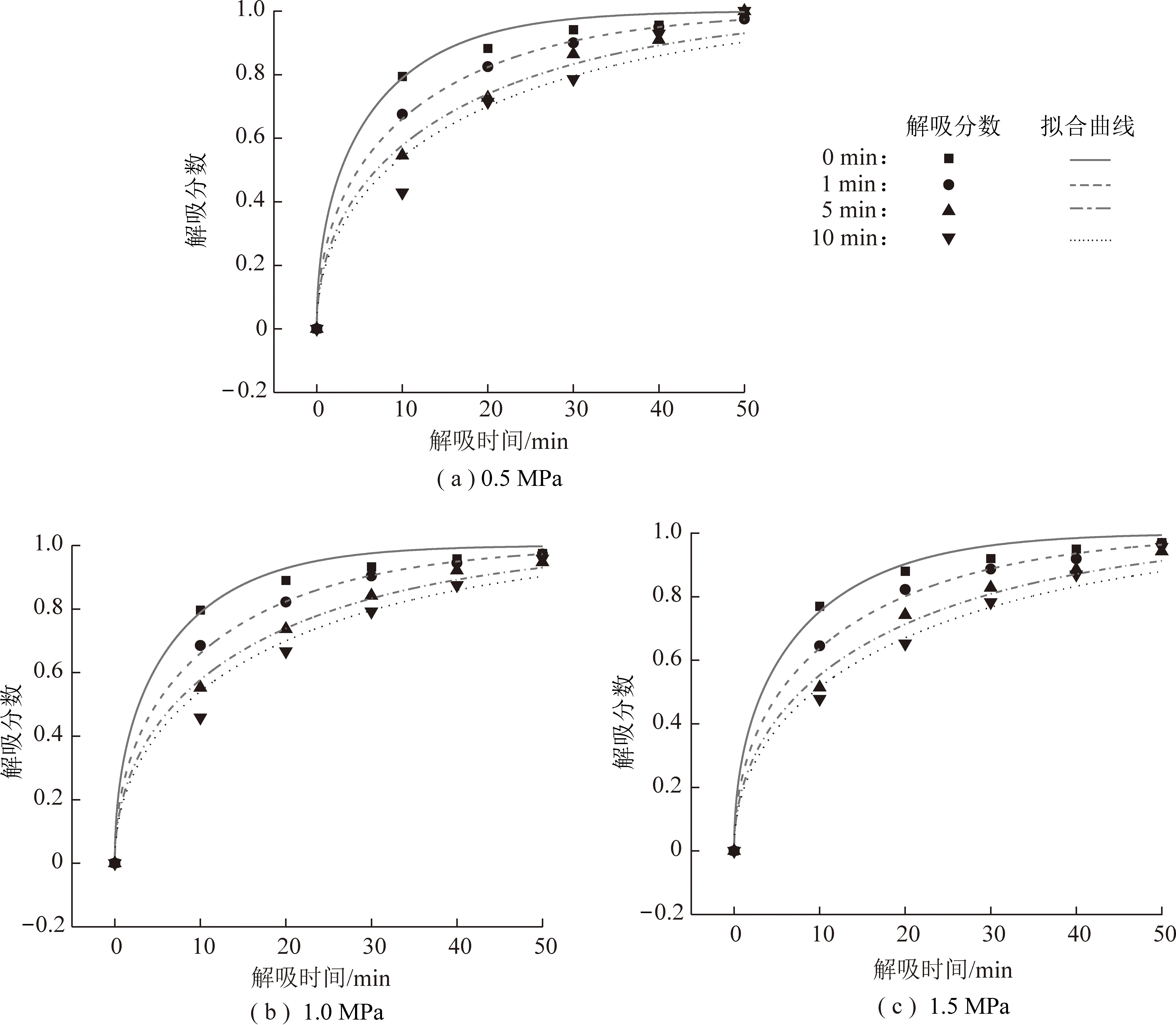
图4 单孔扩散模型拟合曲线
将拟合得到的表观扩散系数有效值与损失时间对应起来,形成如图5的关系曲线。煤样瓦斯表观扩散系数有效值随着损失时间的增加而逐渐降低。此种变化规律与以往文献中瞬态扩散系数的变化规律相似,其本质是由于初期瓦斯解吸时存在游离态瓦斯,游离态瓦斯高速逸散时,产生的随体流动加大了整体表观扩散系数有效值,导致试验瓦斯解吸量比实际煤样上吸附的瓦斯解吸量更大,形成了更为剧烈的传质效果。
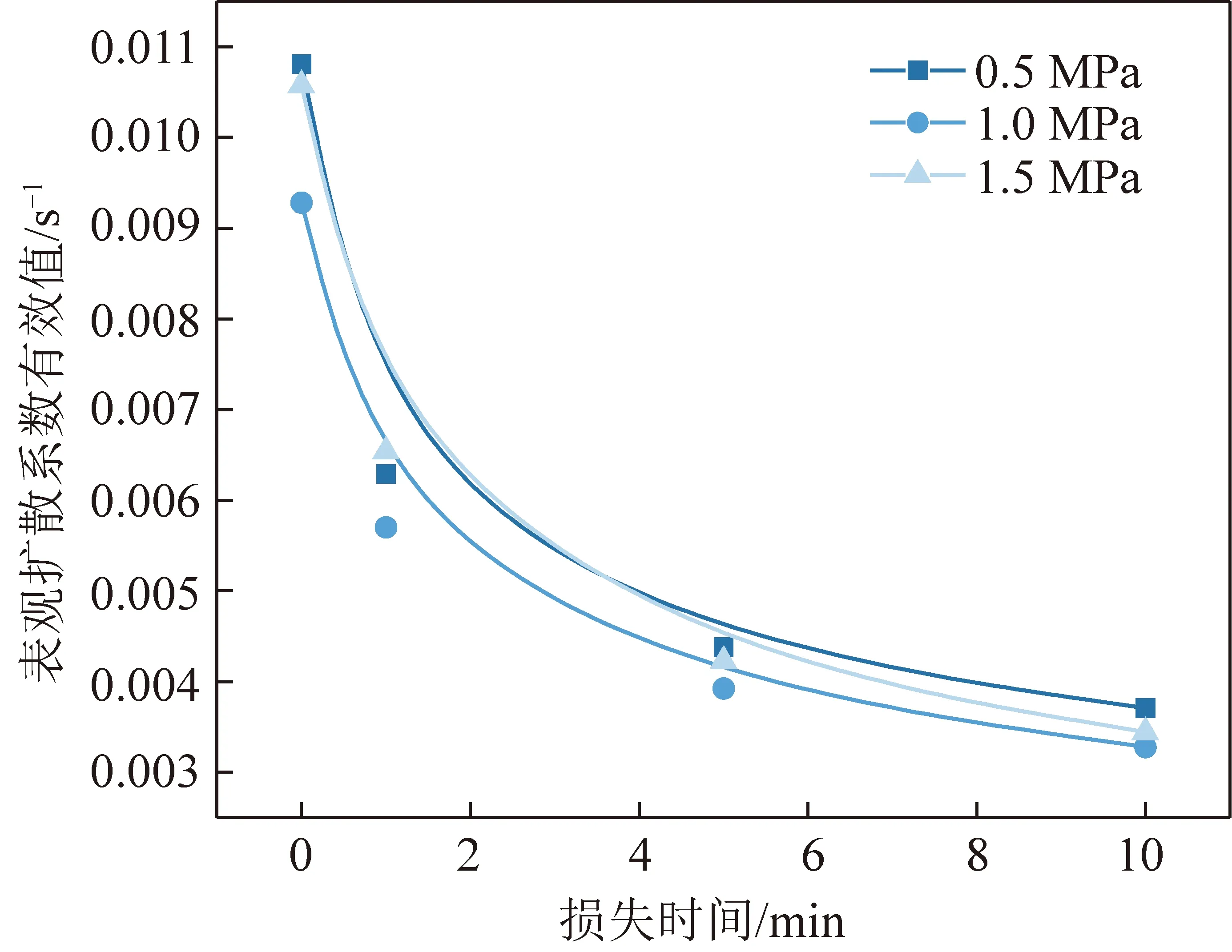
图5 不同损失时间下的表观扩散系数有效值变化
3 讨 论
3.1 类瞬态扩散衰减模型的不同损失时间下表观扩散系数衰减模型
参考瞬态扩散系数的建模思路,采用类伪一级动力学模型对不同平衡压力条件下不同损失时间的表观扩散系数有效值进行拟合(式(2))。伪一级动力学方程是在反应动力学基础上建立的,其以指数函数为特征,建立了反应时间和反应质量的关系,适合描述大多数动力衰减过程,包括气体吸附传质过程。LOSKUTOV等曾指出自扩散系数与衰减时间存在指数函数的关系,而自扩散系数与表观扩散系数在低压段可近似为等价。因此,参照上述思路可建立下述衰减关系:
=exp(-)+
(2)
式中,为不同时刻的表观扩散系数有效值,s;为最终时刻的表观扩散系数有效值,s;,为待定系数。
为了更好地表示损失时间对表观扩散系数有效值的影响,定义损失时间修正因子,其为每个损失时间下的表观扩散系数有效值与最终时刻的表观扩散系数有效值的比值,即
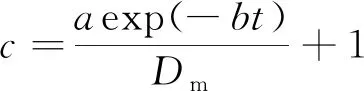
(3)
则不同损失时间的修正因子与最终时刻的表观扩散系数有效值的乘积即对应损失时间的表观扩散系数有效值,即
=
(4)
采用式(2)对图5中的数据进行拟合,并根据式(3),得出待定系数与修正因子(表3)。需要指出的是,由于选取点数量及测试方法的限制,使得各系数的变化规律不明显,这对解释待定系数的物理意义有所干扰,但仍能定性地说明一些问题。当=0时,初始表观扩散系数有效值为+1,则决定了表观扩散系数有效值的初始大小;而则决定了表观扩散系数有效值衰减的快慢。

表3 不同压力下最终时刻表观扩散系数有效值拟合结果
3.2 游离瓦斯流动与吸附瓦斯扩散的竞争关系
怎样厘定游离瓦斯在整个解吸过程中的比例是确定基质吸附态瓦斯表观扩散系数精准与否的关键,而怎样描述裂隙中的游离瓦斯流动与基质中的孔隙扩散则又是其中的重中之重。为了简化建模难度,煤中瓦斯解吸的过程可以假设为原有游离瓦斯先行流动解吸,之后吸附态瓦斯逐渐扩散形成新游离态瓦斯流的2个独立关联的过程,此种假设与渗透率模型中常见的双重孔隙介质假设相似。根据渗透率模型中常见的平板模型,可以假设裂隙中的游离瓦斯是在对于截面积为、长度为的平板孔隙中运移(图6),则根据零级动力学方程,有
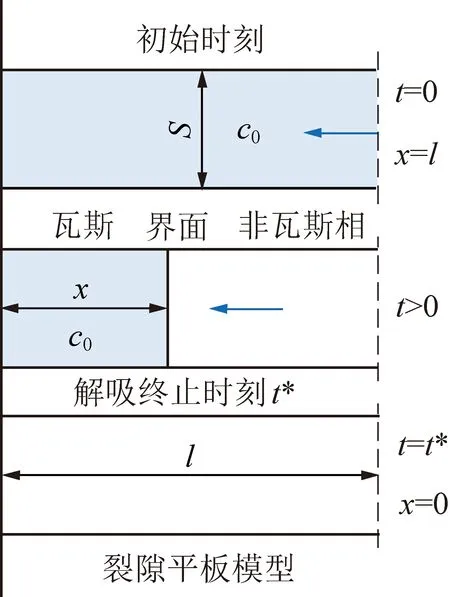
图6 游离瓦斯运移示意

(5)
式中,为时刻解吸出的瓦斯总质量,g;为零级动力学系数。
当解吸开始时,解吸面将从右向左运移,由于解吸速度快,可假设瓦斯相和非瓦斯相质量浓度在各自区域内均一且与时间无关。则对于任意时刻,扩散面运移至距出口处时,非瓦斯相中逸出的瓦斯总质量为
=(-)
(6)
式中,为瓦斯相中的质量浓度,g/mL。
将式(6)代入式(5),有
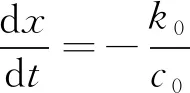
(7)
对于任意的时刻,积分可得
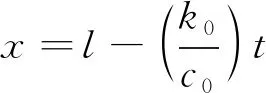
(8)
所以有

(9)
令=,则解吸分数为
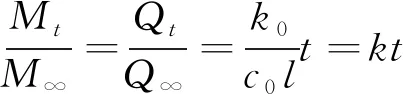
(10)
式中,为系数,=()。
上述推导表明,游离态瓦斯初期解吸速度快,其解吸质量可近似看成与时间呈线性关系。这与张向阳等关于煤样瓦斯解吸量随解吸时间变化关系的试验结果相符:不同压力下钻屑在开始解吸前的一段时间内解吸速度基本上趋势一致。此现象的出现可能是由于解吸初期游离瓦斯占主导地位,解吸速率在该时间段内保持不变。因此,笔者尝试将单孔扩散模型与游离瓦斯线性流动模型有机结合,形成引入游离瓦斯组分贡献的瓦斯全浓度表观扩散模型,即
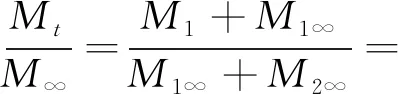
(11)
式中,为游离态瓦斯对宏观解吸的贡献;1-为吸附态瓦斯对宏观解吸的贡献;,为煤粒时刻解吸出的游离态瓦斯和吸附态瓦斯质量;,分别为煤粒最终解吸出的游离态瓦斯和吸附态瓦斯质量。
应当指出的是,式(11)的转换关系虽在形式上符合基质裂隙并联传质的关系,但RUCKENSTEIN等在采用相似方法推导双孔扩散模型时曾指出:在小孔扩散系数与大孔扩散系数比值极小的条件下,意味着此时大小孔2种系统的相互关联很小,则并联传质关系与串联传质关系的差异不大。因此,式(11)仍可用于描述裂隙(大孔系统)和基质(小孔系统)中瓦斯串联传质的关系。将式(1)和式(10)分别代入式(11),可得到
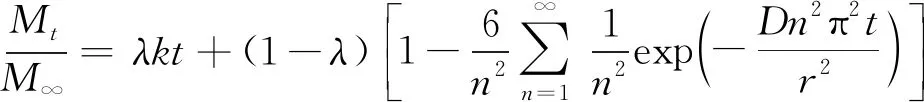
(12)
3.3 游离瓦斯流动与吸附瓦斯扩散在宏观解吸中的控制作用演化
式(12)可用于拟合解吸过程中游离瓦斯与吸附瓦斯共存阶段的瓦斯解吸特性。将之用于拟合图3中的解吸数据,可得到表4和图7的结果。
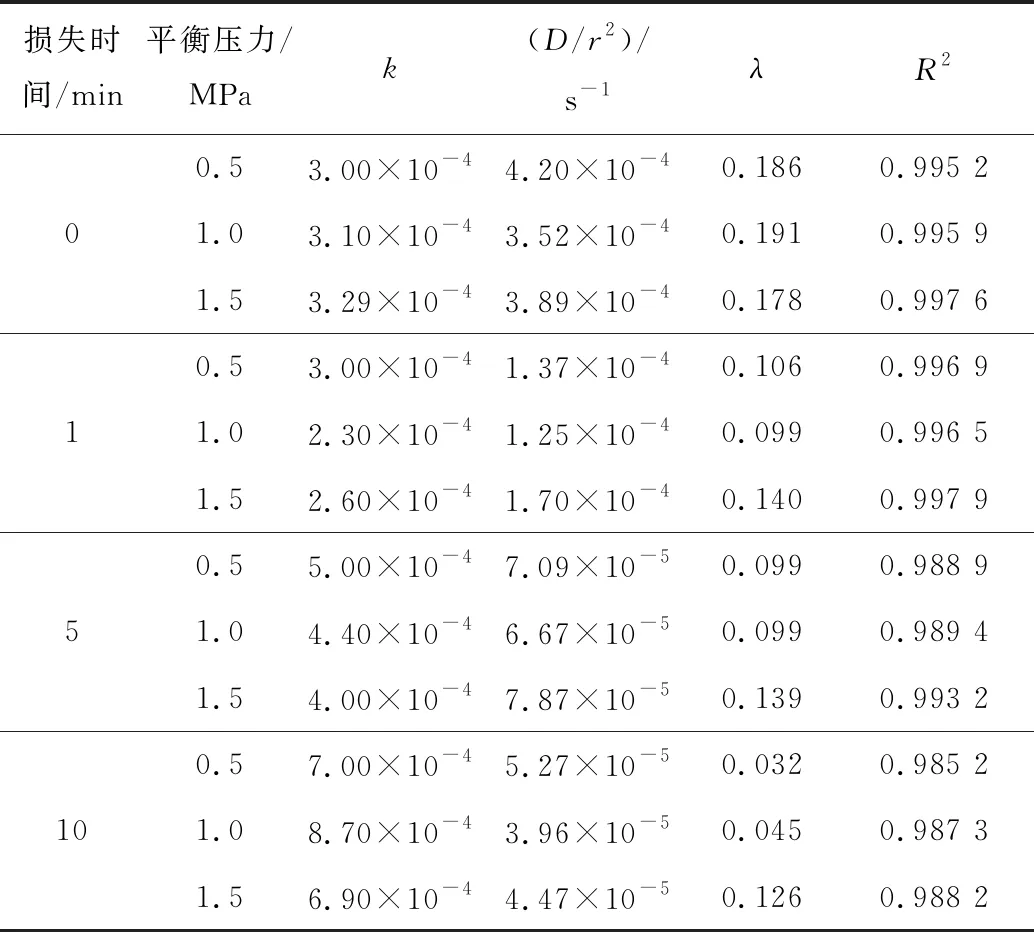
表4 式(12)对试验数据的拟合结果

图7 游离瓦斯与吸附瓦斯对宏观解吸贡献度变化
从图7表4中可以看出,游离瓦斯流动对宏观解吸的贡献在20%以下,这恰好与通常意义上游离瓦斯所占全部瓦斯的比例相似。另外,随着损失时间的逐步推移,游离瓦斯在宏观解吸中的贡献比例越来越小,且随着平衡压力的增加,降低幅度有所减小。当平衡压力为0.5 MPa时,贡献值从0.186降至0.032,降低了83%;当平衡压力为1 MPa时,贡献值从0.191降至0.045,降低了76%,降幅基本不变;当平衡压力为1.5 MPa时,贡献值从0.178降至0.126,降低了29%,降幅显著缩减。此种衰减规律与游离瓦斯含量以及吸附瓦斯含量随压力增高的变化规律有关。由于游离瓦斯含量与压力呈线性关系,而吸附瓦斯含量与压力呈Langmuir关系,因此两者与压力的关系存在3个演化阶段(图8):① 斜率关系突变点之前,吸附瓦斯含量要大于游离瓦斯含量,且吸附瓦斯含量增长速率也要大于游离瓦斯含量增长速率(>且′>′);② 斜率关系突变点之后、大小关系突变点之前,吸附瓦斯含量要大于游离瓦斯含量,但吸附瓦斯含量增长速率小于游离瓦斯含量增长速率(>且′<′);③ 大小关系突变点之后,吸附瓦斯含量要小于游离瓦斯含量,此时成为负吸附现象(<)。试验结果中,0.5 MPa和1 MPa下的游离瓦斯贡献降幅相似,说明斜率关系突变点在0.5~1.0 MPa附近,而之后在1.5 MPa时游离瓦斯贡献降幅明显缩减,说明游离瓦斯含量较多且逸散更为持久,使得相同损失时间条件下逸散出的游离瓦斯量占总游离瓦斯量的比例缩小,正好处于阶段②之后。

和朗格缪尔常数;游离瓦斯体积;P,P0—目标瓦斯压力和标况气压;T,T0—目标温度和标况温度
3.4 K1及损失量有效测算时间区间判定

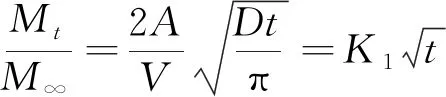
(13)
式中,为煤样的外部表面积;为煤样的总体积。
将式(2)代入式(13),可得

(14)
对比式(13)和式(14),可得
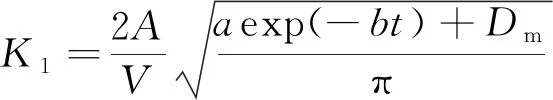
(15)

3.5 瓦斯损失量推算的高拟合度模型

对于式(12)而言,在短时间内的扩散过程内,无论扩散介质形状如何,扩散分数和扩散时间的平方根都具有很好的线性关系。对于单孔扩散模型而言,当解吸时间小于600 s时,即10 min以内的数据,有如下简化关系:

(16)
式(16)可用于拟合短时间内的扩散曲线,适合推导和瓦斯损失量。而根据RITGER和PEPPAS的研究成果,存在以下的简化关系:
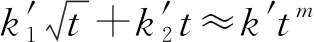
(17)
式中,′和′为任意的比例系数;′为新生成的比例系数;为新生成的指数。
将式(17)的系数进行变换,令′=(1-),′=,则有
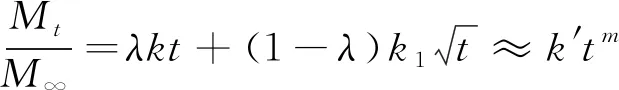
(18)

图9为平衡压力为1.5 MPa的解吸曲线,其可看作多个损失时间条件下解吸曲线的叠加集合。而λ的演化规律间接反映了主控角色随时间变化的特征。λ越大,游离态瓦斯对宏观解吸的贡献越大,主控作用越强,线性段就越大。

图9 新模型对前10 min解吸数据的拟合结果示例(平衡压力为1.5 MPa)

4 结 论
(1)瓦斯解吸过程分为游离瓦斯流动主控阶段、过渡阶段和基质吸附瓦斯扩散主控阶段。其中瓦斯曲线在游离瓦斯流动主控阶段和基质吸附瓦斯扩散主控阶段分别符合线性和单孔扩散模型规律。
(2)随着损失时间的加长,游离瓦斯流动对宏观解吸的作用减弱,瓦斯表观扩散系数有效值逐渐降低,并稳定在10~10s数量级。



