基于TFA-DC到时拾取的双震相微震震源定位方法

贾宝新，李 峰

(辽宁工程技术大学 土木工程学院，辽宁 阜新 123000)

随着深部矿产资源开采的快速发展，针对深部区域开采环境的安全性研究日益深入。由于蕴含巨大的地应力与构造应力，深部区域的矿产资源在开采的同时会伴随着一些诸如冲击地压、采空区垮落、岩爆、巷道片帮冒顶等环境与安全隐患。

为了监测与预防这些安全隐患，如今矿产资源开采过程中普遍采用微震监测技术对灾害源进行监测定位，其中微震源定位方法是微震监测的核心内容，也是提高灾害预测精确度的关键。提高微震源定位方法的定位精度一直是微震监测技术研究的重点与难点。

微震定位方法主要是利用检波器收集到的微震信号进行微震波初至到时拾取，并将其与各检波器空间坐标一同代入优化算法中，从而反演出微震事件发生位置及时刻。因P波波速高于其他震相，所以当P波到达检波器时，其微震信号波形不易被干扰，进而有助于其初至时刻的精确拾取，故如今国内外学者主要是通过拾取P波初至到时来进行反演定位或者基于P波初至到时对震源定位精度进行相关研究。如王辉等提出的基于单纯形-最短路径射线追踪的微震震源混合定位算法；李楠等提出的基于L1范数统计的单纯形定位方法；王云宏等针对传统定位方法过度依赖走时精度问题所提出的改进定位目标函数的差分进化微震定位方法；姜天琪等提出的基于网格搜索-牛顿迭代法的微震震源定位算法；贾宝新等提出的小尺度下基于高密度台阵和粒子群算法的微震源定位方法；LI等通过研究传感器阵列的空间布局与放置方向提出的可提高定位精度的传感器网络优化原则；JENNIFER等通过优化台站空间布局提出的改进多阵列震源反演定位方法；SOLEDAD等利用方位角优化结合模拟退火与粒子群算法提出的改进全局搜索算法。在此基础上，也有对双震相震源反演定位进行研究的，如TIAN等利用P波、S波初至到时时差提出的实时更新速度模型的微震定位事件交叉双差反演方法；王志刚通过研究不同台阵分布对应的不同双曲面场提出的双波定位原理。

以上研究成果在一定程度上提高了震源定位的精确度并阐明了双震相定位的作用，但依然存在着一些问题：由于其他震相的干扰导致S波难以识取到时的问题；P波单震相与S波单震相在震源定位方面的区别与联系没有阐明的问题；单独使用S波到时的震源定位效果不明的问题。

针对以上问题，笔者利用基于时频分析的下山比较法(Time-Frequency Analysis-Downhill Comparison Method，TFA-DC方法)对微震事件信号进行处理，将其所能拾取到的P波精确到时与S波峰值代入整合波速后的双震相目标函数中，并使用粒子群算法进行目标函数最小值搜索，以此提出了同时使用P波精确到时与S波峰值到时的双震相微震定位方法——基于TFA-DC到时拾取的双震相定位方法(TFA-DC-double seismic phases location method，TD-DL方法)。

1 微震定位基本原理

目前，微震源反演定位广泛使用基于走时残差理论的震源定位方法。理论计算走时与实际观测到时的差即走时残差，利用计算走时残差的不同方法，可构造出不同的微震定位目标函数。对应震相应选取相应的目标函数，笔者选取分别应用于单震相定位与双震相定位的2种目标函数。

1.1 单震相目标函数

现有微震定位方法通常采用P波单震相进行到时拾取及震源反演定位。与其他震相相比，P波震相初至响应特征明显，更利于精确拾取到时，所以其定位精度也较高。笔者采用理论计算走时与实际观测到时差值的数学期望作为发震时刻的估计值，从而得到P波单震相的走时残差计算公式：

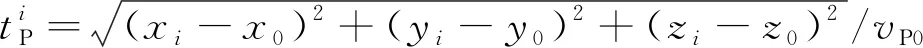
(1)

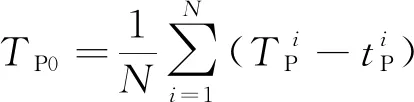
(2)

(3)

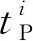
同理可得S波单震相的走时残差计算公式：

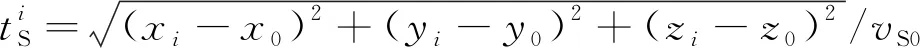
(4)

(5)

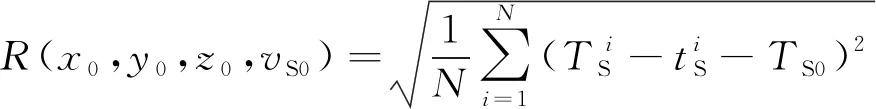
(6)

1.2 双震相目标函数

单一微震事件通常同时包含P波、S波、面波、反射波等多种震相信息，而除P波外的其他震相因重叠、干扰等问题，通常难以用于定位计算。相关研究表明，对于提高震源定位精度而言，同时使用2种震相的目标函数定位精度要高于只使用单一震相的目标函数。

故此笔者引入同时使用P波单震相与S波单震相的双震相目标函数，并对其中双震相的波速进行整合，其目标函数如下：

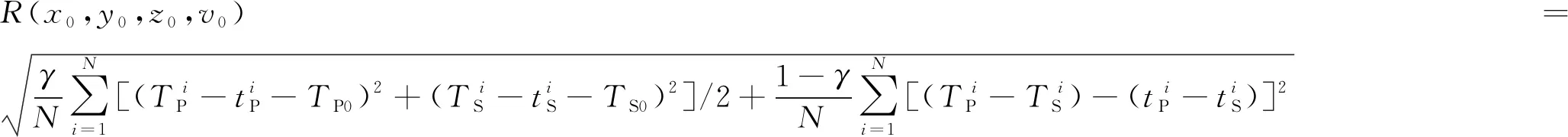
(7)

式中，(,,,)为双震相的走时残差；为震相传播速度，m/s；为均衡系数，取值为0～1。

因为P波、S波波速未知且时刻发生变化，该变化在传播过程中的变化幅度也不相同，所以独立使用2种波速代入计算后很可能导致算法无法收敛。对于定位精度而言，因波速结构的不确定性，同时代入2种单震相的平均波速进行定位反演计算会使定位精度降低。鉴于以上问题，笔者将P波与S波的平均波速设为相同值——震相传播速度，并与所求震源空间坐标，，一同代入粒子群算法中计算。一则可以避免预先测速，达到实时监测的效果；二则可以降低波速结构对定位精度的影响，使得目标函数尽可能趋于最小值；三则可以提高目标函数的收敛性，因为不同发震条件下，岩土体破裂程度不同，从而使挤压产生的P波与剪切产生的S波的波速均非恒定值，而在小尺度微震监测下，P波与S波的传播距离短，其速度变化量较小，故单次微震事件中P波与S波的波速比值可视为常数，即震相传播速度可表征为二者的统一传播速度。

改进双震相目标函数的作用原理是根据已有检波器坐标及双震相到时形成含有4个自变量的方程。在定义域内，利用全局搜索算法对目标函数最小值进行搜索，最小值对应的4个自变量数值即为所求震源反演坐标及其对应的震相传播速度。

1.3 P波和S波到时联合拾取方法

(1)TFA-DC方法简介。TFA-DC方法是一种可同时获取微震信号P波精确到时与S波峰值到时的到时拾取方法。该方法首先通过分析原始信号的语谱图与功率密度谱图获取背景噪声的位置和规律以及P波、S波初至前后微震信号的频率、振幅、能量变化。然后根据相关算法进行第1次带通滤波，过滤掉规律且功率大于P波、S波信号的高、低频背景噪声，使功率密度谱图中S波的主频清晰显现。

随后以S波主频为圆点，规定滤波范围为半径进行第2次带通滤波，使信号图像更加平滑且适宜迭代比较。由于此半径的选择会涵盖P波以及S波的主频范围，并且P波波速要大于S波，所以滤波后波形中P波精确到时所对应的P波初至波形以及S波峰值到时所对应的全信号振幅波形均可清晰显现，且在大多数情况下不会产生干扰或遮盖。

最后通过将全子波振幅的数学期望设置为阈值，并遵循P波和S波功率大小、到达先后、波形重叠三大关系对滤波后信号进行下山比较以此获得P波精确到时，以及P波震相右侧第1个波峰所代表的S波峰值到时。

(2)TFA-DC方法的有效性证明。现利用连续小波变换理论(Continuous Wavelet Transform，CWT)，并以图5所示模型试验信号为例，对TFA-DC方法所拾取的P波精确到时与S波峰值到时加以说明，原始微震信号及尺度如图1所示。

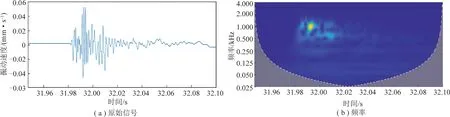
图1 原始微震信号及尺度

排除500 Hz以下的规律且全程持续的背景噪声，通过图1中信号图与尺度图对应分析可知，该微震信号能量变化主要可分为4个过程：31.983～31.992 s为第1次能量突变，因其最早到达，故可视为由P波到达所引起的振动响应；31.992～31.999 s为第2次能量突变，因其能量大于P波并且仅次于P波到达，故可视为S波到达所引起的振动响应；31.999～32.005，32.005～32.019 s分别为第3，4次能量突变，因其到达晚于P波与S波，故可判断为反射波、面波等其余震相。

综上可证明TFA-DC方法所拾取2种到时分别为的微震信号的P波精确到时与S波峰值到时。

(3)到时拾取特点。因带通滤波对突变信号有一定的平滑作用，信号突变处会产生子波振幅递增或递减的平滑过渡现象，以此导致TFA-DC方法中P波精确到时拾取实则早于其真实到达时刻；因检波器所采集的S波信号自到达至达到峰值需要一定的时间过程，并且有时会叠加其他震相于其上，故S波峰值到时实则晚于其真实到达时刻。所以单独使用上述P波或S波单震相到时数据进行震源反演定位，可能会造成定位结果相较真实震源有一定的偏移。

1.4 粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)是一种常用的广域随机搜索算法，其核心思想是共享各个子个体所历经的目标函数值信息，使得全部子个体利用所有已知的目标函数值信息进行最优化的定向移动，直到某个子个体找到目标函数的全局最优解。其速度和位置进化方程如下：

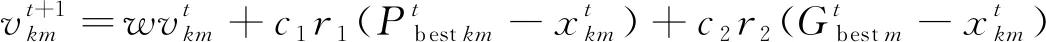
(8)

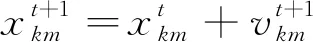
(9)

选定目标函数并导入相关到时及检波器空间坐标信息后，使用粒子群算法进行目标函数最小值搜索。通过迭代搜索所得的目标函数最小值所对应的自变量数值即所求震源的空间坐标。

1.5 TD-DL方法

笔者提出的TD-DL方法是包括一整套微震定位解决方案的新型定位方法，其中包含可同时拾取P波精确到时与S波峰值到时的TFA-DC双震相到时联合拾取方法、整合波速后的双震相目标函数、粒子群全局搜索算法，以上方法相结合便构成了可自动拾取到时并定位计算的TD-DL方法。

2 模型试验

利用超高频多通道构造活动监测仪对摆锤撞击产生的微震信号进行处理分析，以此探究单震相定位方法与TD-DL方法在震源反演定位方面的区别与联系，并对TD-DL方法的原理及实际震源定位效果进行验证。

2.1 模型建立

本试验模型长为2.3 m、宽为1 m、高为1.3 m，采用石英砂、石膏、石灰、水混合后分层堆砌而成，其质量配比约为6∶3∶1∶2。22个检波器在模型脱模后钻孔嵌入墙体，检波器三维空间坐标见表1。

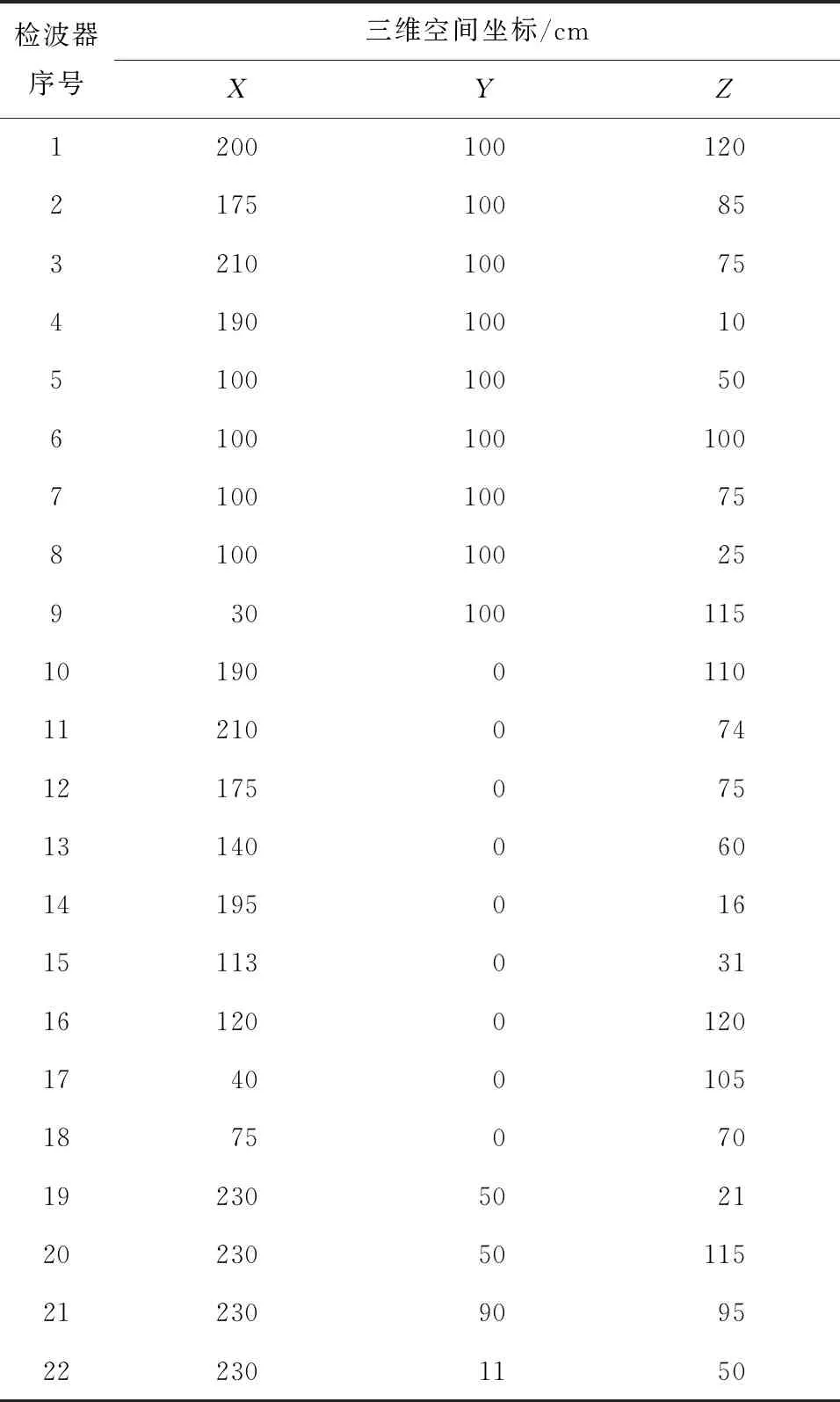
表1 各检波器三维空间坐标

图2中黑色球体为单分向微震检波器，其周围数字为检波器序号；黑色立方体为撞击位置，箭头指向黑色立方体的字母为震源序号。10～18号检波器按规定位置设置在模型的=0面，此面记作面；19～22号检波器按规定位置设置在模型的=230 cm面，此面记作面；1～9号检波器按规定位置设置在模型的=100 cm面，此面记作面。

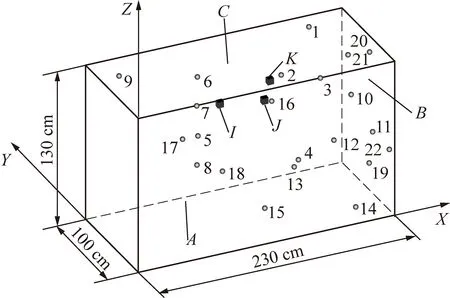
图2 试验布局

2.2 监测设备

本试验采用采样频率为100 kHz、可监测频带宽度为0～50 kHz的超高频多通道构造活动监测仪(Antenna-Ⅲ)记录单摆撞击模型表面产生的微震信号，设备参数见表2，超高频多通道构造活动监测仪各组成部分如图3所示。

表2 超高频多通道构造活动监测仪设备参数

图3 超高频多通道构造活动监测仪

2.3 试验过程

本试验采用球体定长单摆撞击模型指定位置，连接钢球的连接线采用长为30 cm的棉质线，撞击球体采用半径为1 cm的钢球。模型制作好后带模具养护7 d，以防开裂。卸下模具后，保持开窗通风且每天至少5 h日照。30 d后检查时，已可确保模型完全干透。因制作材料本身的脆性，钢球撞击模型表面时可使表面下陷0.3 cm左右，所以此过程可以保证模型受挤压破坏产生P波，也可保证模型挤压破坏区同时也受剪切破坏，从而产生S波。

(1)撞击位置。试验设计撞击位置共3个，分别命名为“震源”、“震源”、“震源”，其三维空间坐标见表3。

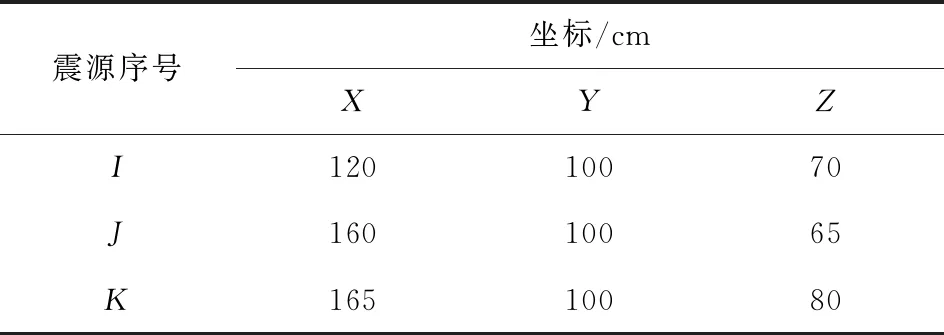
表3 各震源三维空间坐标

(2)撞击方式。在试验准备阶段将3个撞击位置用记号笔做好标记，试验时先将钢球自然悬挂并刚好接触模型表面的指定撞击位置。随后将钢球拉至垂直于模型表面5 cm后放手，使之自由下落并撞击指定位置，表3中的3个位置各撞击10次，试验现场照片如图4所示。

图4 试验现场

(3)数据收集。准备好钢球和连接线并将其安排在指定位置后，开启超高频多通道构造活动监测仪并对其进行测试，完毕后进行撞击试验，完成后将所得试验数据保存至硬盘指定位置。

2.4 预先波速分析

通过真实震源位置与P波精确到时、S波峰值到时正演P波、S波的平均波速，结果显示：P波波速为5 600～7 400 m/s，S波波速为5 100～6 800 m/s，震相传播速度为5 100～7 400 m/s。震相传播速度的变化范围涵盖了P波、S波2种单震相波速的变化范围，说明震相传播速度可以很好的表征2种震相的传播。P波平均波速大于S波平均波速，并且P波波速的变化范围略大于S波波速，说明本试验模型的密实度较高，波速变化规律也与岩石中传播相近。

3 单双震相定位分析

通过对模型试验所得微震信号进行处理并获取到时数据后，利用单、双震相目标函数以及粒子群算法获取3种到时组合的反演定位结果。最后通过3种到时组合所得震源反演坐标与定位误差的对比分析，对TD-DL方法的有效性进行验证。

3.1 到时拾取

利用TFA-DC方法处理共得到震源、震源、震源的各10组到时数据，每组到时数据包含P波精确到时22个、S波峰值到时22个，最后一共得到3处震源的1 320个到时数据。TFA-DC方法拾取双震相到时如图5所示(对应原始信号如图1所示)。图5中S波信号振幅约为P波的6倍，而图1中该比值为3倍，这是由于TFA-DC方法对原始信号进行了连续2次带通滤波，故此信号中P波与S波的信号振幅与特征会较原始信号中的略有不同，但此区别并不会影响到时的拾取，该过程产生的光滑信号反而更有利于TFA-DC方法中下山比较法的执行，使其中迭代比较子波振幅的过程容错率更高。根据1.3.3节所述并对比图1与图5可知，TFA-DC方法所得双震相到时中P波精确到时略早于真实到时，而S波峰值到时略晚于真实到时。故以下着重分析在利用上述到时的前提下，单、双震相定位结果之间的联系与区别。

图5 双震相到时拾取示意

3.2 单、双震相定位结果分析

模型试验定位结果分析的目的是找到P波精确到时与S波峰值到时单独或联合使用时，所得定位结果之间的区别与联系。为方便分析叙述，下述内容只对定位结果的轴与轴坐标进行分析，轴坐标同理，不再赘述。

..震源定位结果

使用P波、S波单震相反演定位计算时，将到时数据与检波器空间坐标数据分别应用于式(3)与式(6)，可得二者的定位结果。TD-DL方法需要将双震相到时与检波器空间坐标数据同时应用于式(7)，可得其定位结果。上述反演定位计算结果如图6所示。

图6 震源I，J，K反演定位结果

..定位结果图像分析

据图6可知，3种到时组合的定位结果大体可描述为：以TD-DL方法定位结果为中心，P波、S波单震相定位结果以相近的距离分布于相反方向的两侧。

相较真实震源而言，TD-DL方法定位结果表现为围绕或邻近于真实震源的四周，而P波、S波单震相的定位结果与真实震源之间呈方向相反但距离同步变化的趋势。

..TDDL方法原理分析

据1.3.3节可知，TFA-DC方法所拾取的P波精确到时较真实到时略早，而所拾取的S波峰值到时较真实到时略晚。这就导致通过二者所得的定位结果会以相反的方向偏移真实震源。通过模型试验证明，二者相对于真实震源所偏移的距离大致相同，可见其到时误差也大致相同。若到时误差完全相同，因目标函数中2种震相所占权重相同，故TD-DL方法定位结果应与真实震源一起分布于2种单震相定位结果的中间位置。但由于二者拾取过程不同，加之现场其余震相的干扰，导致其到时误差不完全相同。在此情况下，得益于增加了S波到时的约束信息，TD-DL方法提高了对检波器坐标、双震相到时等已知信息的统合能力，减小了到时误差不同的影响。通常对于不同的传播路径，每个传感器接收的S波信号自到达至峰值的上升时间是不一样的。各检波器中S波到时误差的不同会因误差叠加效应而增加其定位误差，从而使得单独使用S波峰值到时的定位精度要低于单独使用P波精确到时的定位精度，但目标函数求最小值的过程会使TD-DL方法定位结果趋于2种单震相到时误差更小的一方，使其定位结果可以在一定程度上偏向真实震源，从而提高了定位精度。

综上所述，在使用TFA-DC方法拾取P波、S波单震相到时的基础上，TD-DL方法可在一定程度上抵消P波、S波单震相计算所得的定位误差，并使定位结果趋于2种单震相定位精度高的一方，从而达到提高震源反演定位精度的效果。

3.3 单、双震相定位误差分析

对震源、震源、震源的各10组到时数据进行反演定位计算，共处理得到P波、S波单震相以及TD-DL方法定位结果各30个。现将以上各定位结果距真实震源的距离作为定位误差，并将定位误差按照震源、震源、震源分组作图，所得结果如图7所示。

自图7可知，TD-DL方法定位精度与稳定性要高于P波、S波单震相定位。定位精度可用定位误差平均值表示，定位稳定性可用定位误差标准差表示，各震相在不同震源下的定位精度与稳定性见表4。

图7 震源I，J，K反演定位误差

由表4可知，震源下TD-DL方法定位误差平均值分别为P波、S波的23.0%和18.0%；震源下TD-DL方法定位误差平均值分别为P波、S波的24.6% 和18.8%；震源下TD-DL方法定位误差平均值分别为P波、S波的24.5%和20.1%。震源下TD-DL方法定位误差标准值分别为P波、S波的50.4% 和32.8%；震源下TD-DL方法定位误差标准值分别为P波、S波的42.6%和44.5%；震源下TD-DL方法定位误差标准值分别为P波、S波的67.7% 和35.4%。

表4 各震相在不同震源下的定位效果分析

由此可见，同时使用P波精确到时与S波峰值到时的TD-DL方法的定位精确度与稳定性要优于P波、S波单震相定位方法。

3.4 检波器布置对定位精度的影响

为了探究检波器布置对定位精度的影响，首先将定位误差分别在各坐标轴上做投影，获得各轴的轴向定位误差，随后通过作图分析二者之间的对应关系。

..轴向定位误差

轴向定位误差见表5，其中轴向定位误差为此震源下对应震相的定位结果与真实震源的之间的距离在对应坐标轴上的投影的平均值。

表5 各震相在不同震源下的轴向定位误差

..检波器布置与定位精度的关系

以定位精度最高的TD-DL方法所得的定位结果为例说明检波器布置与定位精度的关系，其他方法所得结论相同，以下不再赘述。

由图2可知，10～18号检波器位于模型面，19～22号检波器位于模型面，1～9号检波器位于模型面。已知在模型面上轴坐标固定等于0，所以此面的检波器对于轴坐标没有变化范围，即此面对于轴与轴是自由面。同理可知模型面为轴与轴的自由面，模型面为轴与轴的自由面。

故轴上坐标可变的检波器为1～18号，共18个；轴上坐标可变的检波器为19～22号，共4个；轴上坐标可变的检波器为1～22号，共22个。各坐标轴上的平均定位误差与对应坐标轴上坐标可变检波器数量之间的关系如图8所示。

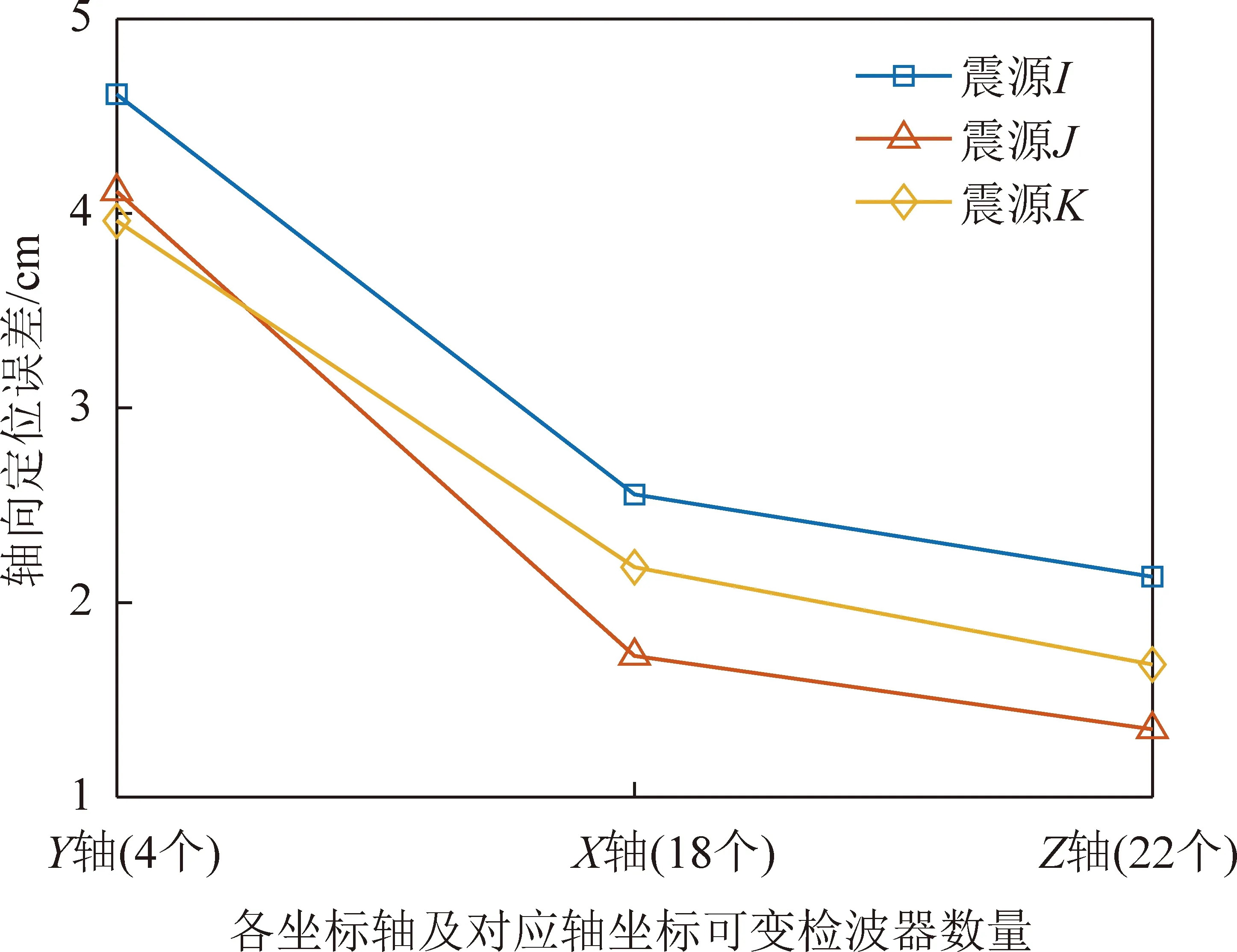
图8 轴向定位误差与对应轴坐标可变检波器数量的关系

根据相关理论，检波器空间密度越高，则震源反演定位误差越小，而对于垂直于各坐标轴的面而言，通常将检波器布置于此类面上相较于布置于监测范围内部来的容易，故此若找到此类面上检波器布置个数与定位误差之间的关系，便可优化检波器空间布置并减小人力物力浪费。

由图8可知，各坐标轴上坐标可变检波器的数量与定位结果在相应坐标轴上的误差呈负相关关系。换言之，高精度定位对检波器空间高密度布置的要求可简化为检波器在各轴对应自由面上的高密度布置，或者说在一定监测范围内，某一坐标轴上坐标可变的检波器越多，定位结果在此轴上的表现便越为精准。

4 工程验证

为了进一步证实TD-DL方法在震源反演定位方面的优越性和可靠性，选取某矿微震监测工程中的矿震信号进行到时拾取及反演定位计算，并通过与P波、S波单震相的定位计算结果进行比较，以此对TD-DL方法进行验证。

4.1 到时拾取

选取不同时期发生的3次矿震所产生的微震信号，并将其分别命名为KZ-1，KZ-2，KZ-3。使用TFA-DC方法对以上3组微震信号进行到时拾取，滤波处理后所得到时拾取如图9所示，所得P波精确到时与S波峰值到时数据见表6。

图9 矿震信号到时拾取示意

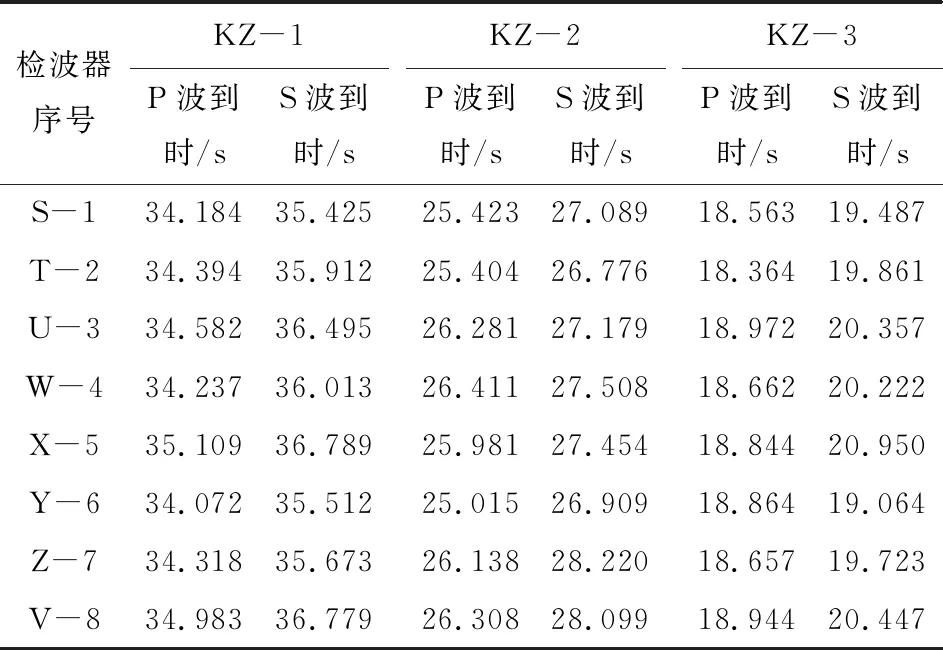
表6 矿震信号P波与S波到时数据

4.2 检波器布置

矿山微震监测工程检波器布置在地表以下2 m深处，仅用于二维监测，即监测震源位置的轴与轴坐标，故检波器的坐标变化范围主要分布在轴与轴，其坐标见表7。

表7 矿山各检波器三维空间坐标

4.3 定位结果分析

为增加双震相到时的约束信息，提高定位算法的收敛性与定位精度，在计算时除检波器轴、轴坐标外同时导入轴坐标协同定位，定位结果只采用轴、轴坐标。虽检波器轴坐标变化范围远小于轴与轴，但由于轴坐标的加入，算法可以增加收敛容错率并减小收敛后的目标函数值。由此说明加入了轴坐标后，可达到提高定位精度的效果。导入检波器坐标及到时数据后，利用粒子群算法进行反演定位计算，其结果见表8，各震源真实坐标见表9。

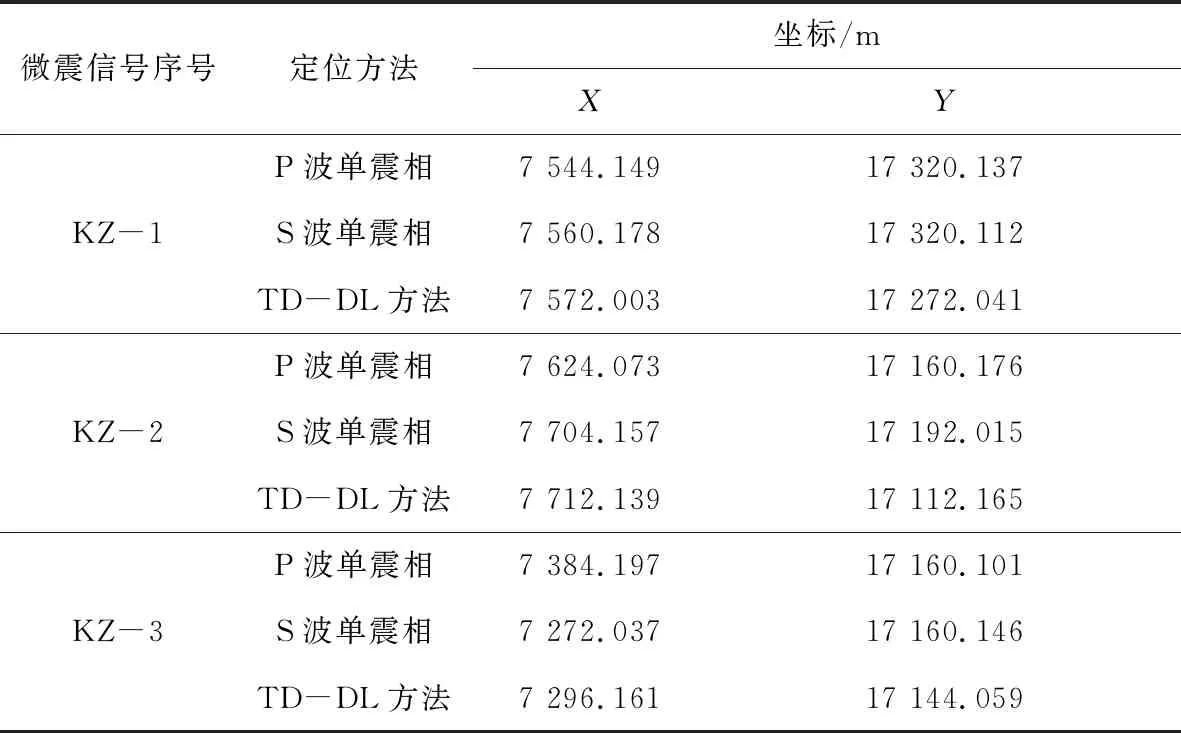
表8 矿震信号各震相定位结果

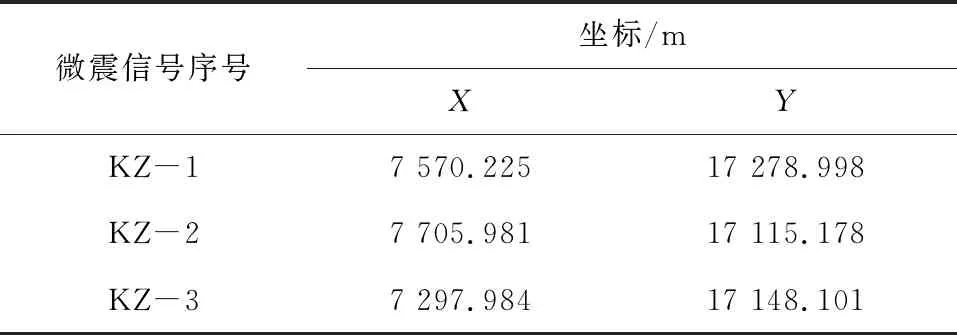
表9 矿震各震源真实坐标

将上述反演定位结果距离真实震源的距离定义为定位误差，各震相的定位误差见表10。由表10可知，在震源KZ-1下，TD-DL方法定位误差分别为P波、S波单震相的14.8%和17.1%；在震源KZ-2下，TD-DL方法定位误差分别为P波、S波单震相的7.3% 和8.9%；在震源KZ-3下，TD-DL方法定位误差分别为P波、S波单震相定位误差的5.2%和15.9%。

表10 矿震信号各震相定位结果分析

由此可见，TD-DL方法对比P波、S波单震相定位方法，在工程现场数据处理方面更为精准且稳定，说明该方法是一种有效的震源反演定位方法。

5 结 论

(1)TD-DL方法由于S波到时约束信息的增加以及目标函数的最小值趋向作用，提高了对检波器坐标、双震相到时等已知信息的统合能力，减小了2种单震相到时误差不同的影响，并使其定位结果趋于2种单震相定位结果较真实震源误差更小的一方。故在TFA-DC方法拾取P波、S波单震相到时的基础上，TD-DL方法可在一定程度上抵消P波、S波单震相计算所得的定位误差，从而达到提高震源反演定位精度的效果。

(2)TD-DL方法的定位精确度与稳定性要优于P波、S波单震相定位方法。模型试验下，TD-DL方法定位误差平均值分别为P波、S波单震相定位的23.9%和18.9%；TD-DL方法定位误差标准差分别为P波、S波的50.9%和36.9%。工程数据下，TD-DL方法定位误差平均值分别为P波、S波单震相定位的8.1%和12.6%。

(3)各坐标轴上坐标可变检波器的数量与定位结果在相应坐标轴上的误差呈负相关关系。高精度定位对检波器空间高密度布置的要求可简化为检波器在各轴对应自由面上高密度的布置，即在一定监测范围内，某一坐标轴上坐标可变的检波器越多，定位结果在此轴上的表现便越为精准。