韧性视角下科技型中小企业创新风险防范研究

赵伟 吴松强 吴琨

[摘要]针对科技型中小企业日益增加的创新风险与竞争压力，构建了政府、投资者和科技型中小企业三方利益主体的行为决策演化博弈模型，利用Vensim软件进行模拟仿真，研究和分析了各主体策略抉择的影响因素与演化稳定性。研究发现：当投资者信息识别支出小于投资收益与额外收益之和，且政府支出小于政府的基本收益、额外收益与间接损失之和时，稳定策略为政府采用补贴策略、投资者采用投资策略、科技型中小企业采用培育韧性策略;积极的补贴策略、充足的投资资金以及企业主动的韧性培育策略能更好地帮助科技型中小企业应对创新风险;政府补贴与投资资金存在效用界限，合理的补贴和投资力度能有效抑制科技型中小企业因逐利而产生的冒险冲动行为，促使科技型中小企业采用培育韧性策略。

[关键词]科技型中小企业;政府补贴;风险投资;企业韧性

一、 引言

党的十八届五中全会提出：必须把创新摆在国家发展全局的核心位置，不断推进理论创新、制度创新、科技创新、文化创新等各方面创新1。科技型中小企业作为科技创新的主体，在新的政策引领下，其数量急剧增加，据天眼查数据显示，全国小微企业已达8000万家，占企业总数的70%左右，提供了国家80%以上的就业、70%以上的发明专利、60%以上的GDP和50%以上的税收2。科技型中小企业的快速发展推动了我国现代化经济体系建设，促使我国科学技术不断前进，科技型中小企业已逐渐成为引领中国经济增长的新主体[1]。

然而对科技型中小企业而言，创新即意味着高风险与高投入。创新的高风险性、正外部性等特征，使得企业在创新投入方面往往束手束脚，在经营过程中也大多是“重生产、轻创新”[2]。复杂的外部环境和资产规模小、偿债能力弱等因素也使得科技型中小企业在创新过程中更易出现不确定性，普遍存在融资难、融资贵等问题[3]。新冠疫情的到来更是加剧了科技型中小企业所面临的创新风险，给企业带来了灾难性的打击。据相关数据不完全统计，仅2020年，全国有超过300万家企业注销倒闭，其中超过90%以上为中小型企业。然而，同处在VUCA环境中，为何有些企业能够化险为夷，而有些企业却难以幸免于难，“韧性”是导致出现这两种结果的关键因素[4]。科技型中小企业在创新过程中，当面临技术壁垒、资金困境或其他影响因素干扰时，企业会显现出适应、恢复、重生的本能，这种本能即为企业韧性。它可以通过对危机的识别、应对和恢复，帮助企业成功应对环境不确定性带来的危机与挑战[5]。

创新作为科技型中小企业发展进步的动力源泉，是企业保持竞争优势的先决条件。然而，很多科技型中小企业目前才刚刚起步，初始资金无法支撑创新所需资源，因此政府补贴和投资资金是科技型中小企业创新发展的重要资金来源。目前，国内外学者对政府补贴和投资资金如何促进科技型中小企业创新风险防范进行了研究，但均未达成一致结论。大多数学者认为风险投资对企业技术创新具有促进作用，投资资金数量影响着科技型中小企业创新风险防范的选择[6]。但是，有学者却发现风险投资对企业技术创新产出无显著影响，在企业快速发展时期，对企业创新甚至产生了抑制作用[7]。因外部影响因素的差异，政府补贴对于企业创新风险防范是否具有正向促进作用仍存在异议。就企业属性而言，政府补贴对中小型民营企业、高风险企业创新具有正向促进作用，而对私人性质企业却具有反向的抑制作用[8]。

通过梳理相关文献发现，大多数文章将政府、投资者视作演化博弈过程中一个变量，很少有学者将其作为一方利益主体，然而政府、投资者和企业之间也存在着博弈行为，并以利益最大化为根本目标[9]。此外也尚未有文章从韧性视角来研究科技型中小企业创新风险防控。鉴于此，本文借助演化博弈和系统动力学理论，构建政府、投资者和科技型中小企业三方利益主体的有限理性行为决策演化博弈模型，分析各参与主体的策略稳定性，通过构建系统动力学模型，研究不同参数数值变化对演化路径的影响，验证中小企业可以通过提高企业韧性，来提高企业创新风险防御力，为科技型中小企业创新风险防范研究提供新的研究思路。

二、 理论分析

1. 政府补贴与企业创新风险

创新有助于企业提升市场竞争力。但科技型中小企业因固定资产规模小、偿债能力弱等因素，在创新活動过程中，常常面临着资金短缺、企业创新效益溢出等问题[10]，即科技型中小企业创新成果在上市后被迅速复制，在不承担创新成本与创新风险的情形下，抄袭者同创新企业一起分享超额利润，从而使得企业因资金回笼不足而无法进行新一轮的创新活动。政府补贴可以缓解以上问题，从资源角度出发，政府补贴直接增加了科技型中小企业创新活动资金，降低了企业因创新投入不足而导致的创新风险。从社会角度出发，政府对科技型中小企业进行补贴，即向外界传达了一种讯息，政府支持该企业创新活动，对该企业创新能力给予了肯定[11]。这种信号可以使得金融机构放宽企业融资约束，帮助企业聚集创新资源，增强企业创新活力。

2. 风险投资与企业创新风险

风险投资作为一种主要投资初创企业的权益投资，被投资企业往往拥有高潜力和高风险。首先，投资机构不顾企业的高风险性并对其进行投资，以期通过协助被投资企业发展，从而获得超额的利润收益，而获得高收益方式之一就是推动企业创新，因此投资机构十分支持企业创新活动。其次，科技型中小企业因起步晚、资产少、风险高等特性，使得传统金融机构无法承担企业的高风险而为企业贷款，但风险投资机构可以利用投资入股、阶段投资、介入管理层参与公司经营管理等方式降低投资风险，从而对科技型中小企业进行投资，使得企业可以进行更多的创新活动，提高企业技术水平[12]。最后，拥有庞大关系网络、丰富专业知识和管理经验的风险投资机构，对科技型中小企业进行投资后，通过技术交流与指导，可以进一步提升企业的经营水平、业务水平和决策水平，通过整合企业创新资源，提高企业创新成功概率[13]。

3. 企业韧性与企业创新风险

韧性源自逆境，企业层面的韧性提升有助于科技型中小企业成功应对环境不确定性和突发事件带来的危机与挑战，帮助企业降低损失、恢复平稳甚至推动企业向前发展[5]。在科技型中小企业经营发展过程中，各种突发事件会改变企业生存环境，破坏企业工作秩序。此时，相较于韧性强度较低的企业，高韧性强度的科技型中小企业在面对突发事件时，能够依据环境变化调整相应的企业策略。企业韧性的提升能够有效提高企业危机识别能力，使得企业更好地应对外部环境变化带来的创新风险，增强企业风险防范能力[14]。此外，科技型中小企业的创新活动能够营造良好的员工工作氛围，提高企业工作效率，降低新环境下企业功能失调的可能性，进而提高科技型中小企业适应力。

三、 模型假设与构建

1. 基本假设

本文借助演化博弈模型来分析政府、投资者与科技型中小企业三方利益主体间的行为冲突和策略选择，做出如下假设：

假设一：政府为参与者1，投资者为参与者2，科技型中小企业为参与者3，三方参与主体均为有限理性的，策略选择随着时间的不断推移，最终稳定在最优策略。

假设二：参与博弈的三方行为主体均有两种策略选择，政府可以采用补贴与不补贴策略，投资者可以采用投资策略也可以采用不投资策略，科技型中小企业可以采用培育企业韧性与不培育企业韧性两种策略。

假设三：政府采用补贴策略的概率为[a 0≤a≤1]，采用不补贴策略的概率为[1-a];投资者采用投资策略的概率为[b 0≤b≤1]，采用不投资策略的概率为[1-b];科技型中小企业采用培育企业韧性策略的概率为[c 0≤c≤1]，采用不培育企业韧性策略的概率为[1-c]。

假设四：[I]为投资者投资资金，[i]为投资者投资收益率，投资者投资收益为[Ii];投资者在进行投资时需对科技型中小企业进行信息识别与评估，[Cb]为投资者信息识别的支出成本;[Ra]为政府采用补贴策略时，政府从企业经营过程中得到的基本收益;[Ca]为政府采用补贴策略时，政府的支出成本，包括财政贴息、税收返还、相关激勵政策等投入资金;[Rc]为科技型中小企业采用培育韧性策略时，企业在经营过程中得到的基本收益;[Cc]为科技型中小企业采用培育韧性时，企业的各项支出成本，包括企业经营的管理投入、韧性培育投入、运营投入等，且[Rc≥Cc]。

假设五：[Ka]为政府采用补贴策略且科技型中小企业采用培育韧性策略时，政府从企业经营过程中得到的额外收益;[Kb]为投资者采用投资策略且科技型中小企业采用培育韧性策略时，投资者从企业经营过程中得到的额外收益;[Kc1]为科技型中小企业采用培育韧性策略且政府采用补贴策略时，科技型中小企业在经营过程中获取得额外收益;[Kc2]为科技型中小企业采用培育韧性策略且投资者采用投资策略时，科技型中小企业在经营过程中获取得额外收益;[Wc1]为政府采用补贴策略时给科技型中小企业带来的间接收益;[Wc2]为投资者采用投资策略时给科技型中小企业带来的间接收益，例如政府补贴与投资者投资使得企业信心高涨。

假设六：[La]为政府采用不补贴策略但科技型中小企业采用培育韧性策略给政府带来的间接损失;[Lc]为科技型中小企业采用培育韧性策略但政府采用不补贴策略给企业带来的间接损失，例如积极性不足、项目宣传力度减小等。从长远来看，由于政府部门的不作为导致科技型中小企业支出成本远大于企业经营获得的基本收益，即[Cc+Lc>Rc]。

2. 模型构建

根据上述假设，政府、投资者与科技型中小企业三方利益主体演化博弈收益矩阵如表1所示。

四、 模型分析

1. 演化博弈均衡点

政府采用补贴策略与不补贴策略时的期望收益[Ma]、[M（1-a）]及平均收益[Ma]分别为：

[Ma=bc（Ra-Ca+Ka）+b（1-c）（-Ca）+（1-b）c（Ra-Ca+Ka）+（1-b）（1-c）（-Ca）]  （1）

[M（1-a）=bc（-La）+（1-b）c（-La）]  （2）

[Ma=aMa+（1-a）M（1-a）] （3）

投资者采用投资策略与不投资策略时的期望收益[Mb]、[M（1-b）]及平均收益[Mb]分别为：

[Mb=ac（Ii-Cb+Kb）+a（1-c）（-I-Cb）+（1-a）c（Ii-Cb+Kb）+（1-a）（1-c）（-I-Cb）] （4）

[M（1-b）=0]  （5）

[Mb=bMb+（1-b）M（1-b）] （6）

科技型中小企业采用培育韧性与不培育韧性策略时期望收益[Mc]、[M（1-c）]及平均收益[Mc]分别为：

[Mc=ab（Rc-Cc+Kc1+Kc2+Wc1+Wc2）+a（1-b）（Rc-Cc+Kc1+Wc1）+（1-a）b（Rc-Cc+Kc2+Wc2-Lc）+（1-a）（1-b）（Rc-Cc-Lc）]  （7）

[M（1-c）=ab（Wc1+Wc2）+a（1-b）Wc1+（1-a）bWc2]  （8）

[Mc=cMc+（1-c）M（1-c）] （9）

通过上述计算可得政府、投资者和科技型中小企业三方利益主体行为演化博弈模型的复制动态方程为：

[F（a）=da/dt=a（Ma-Ma）=a（1-a）[c（Ra+Ka+La）-Ca]]  （10）

[F（b）=db/dt=b（Mb-Mb）=b（1-b）[c（Ii+Kb+I）-I-Cb]] （11）

[F（c）=dc/dt=c（Mc-Mc）=c（1-c）[aKc1+bKc2+（a-1）Lc+Rc-Cc]] （12）

當[F（a）=0]、[F（b）=0]、[F（c）=0]时，可得到8个纯策略系统均衡点，即[E1（0，0，0）]、[E2（0，0，1）]、[E3（0，1，0）]、[E4（1，0，0）]、[E5（1，1，0）]、[E6（1，0，1）]、[E7（0，1，1）]、[E8（1，1，1）];除此之外，系统也可能存在两个纯策略均衡点，即[E9（0，Cc+Lc-RcKc2，CaRa+Ka+La）]、[E10（1，Cc-Rc-Kc1Kc2，CaRa+Ka+La）]，其中[E9]需满足条件为[0<Cc+Lc-RcKc2<1]、[0<CaRa+Ka+La<1]，[E10]需满足条件为[0<Cc-Rc-Kc1Kc2<1]、[0<CaRa+Ka+La<1]。

证明：当[a=0或a=1]、[b=0或b=1]、[c=0或c=1]时，因为[F（a）=0]、[F（b）=0]、[F（c）=0]恒成立，所以，[E1（0，0，0）]、[E2（0，0，1）]、[E3（0，1，0）]、[E4（1，0，0）]、[E5（1，1，0）]、[E6（1，0，1）]、[E7（0，1，1）]、[E8（1，1，1）]均是系统的均衡点;当[a=0]、[0<b<1]、[0<c<1]时，若[c（Ra+Ka+La）-Ca=0]、[aKc1+bKc2+（a-1）Lc+Rc-Cc=0]时，即[F（a）=0]、[F（b）=0]、[F（c）=0]成立，若满足[0<Cc+Lc-RcKc2<1]、[0<CaRa+Ka+La<1]，则[E9（0，Cc+Lc-RcKc2，CaRa+Ka+La）]为系统的均衡点;同理可得[E10（1，Cc-Rc-Kc1Kc2，CaRa+Ka+La）]也为系统的均衡点之一。

2. 均衡点的稳定性分析

根据李雅普诺夫稳定性理论，当雅克比矩阵特征值均为负时，所求均衡点为渐进稳定点[15]。利用雅克比矩阵对各均衡点稳定性进行分析，研究表明，中间均衡点不是渐进稳定点，所以E9、E10两均衡点不是稳定点。系统的雅克比矩阵为：

[J=J11J12J13J21J22J23J31J32J33=∂F（a）/∂a∂F（a）/∂b∂F（a）/∂c∂F（b）/∂a∂F（b）/∂b∂F（b）/∂c∂F（c）/∂a∂F（c）/∂b∂F（c）/∂c]

[∂F（a）/∂a=（1-2a）[c（Ra+Ka+La）-Ca]]

[∂F（a）/∂b=0]

[∂F（a）/∂c=a（1-a）（Ra+Ka+La）]

[∂F（b）/∂a=0]

[∂F（b）/∂b=（1-2b）[c（Ii+Kb+I）-I-Cb]]

[∂F（b）/∂c=b（1-b）（Ii+Kb+I）]

[∂F（c）/∂a=c（1-c）（Kc1+Lc）]

[∂F（c）/∂b=c（1-c）Kc2]

[∂F（c）/∂c=（1-2c）[aKc1+bKc2+（a-1）Lc+Rc-Cc]]

根据表2所求特征值探究均衡点的渐进稳定性。以均衡点[E1（0，0，0）]为例，[E1]雅可比矩阵特征值分别为[λ1=-Ca]、[λ2=-I-Cb]、[λ3=Rc-Lc-Cc]，若满足[-Ca<0]、[-I-Cb<0]、[Rc-Lc-Cc<0]，则均衡点[E1（0，0，0）]为渐进稳定点（ESS），同理可以得到均衡点[E2—E8]的渐进稳定性。根据假设条件和实际情况对表2特征值进行判断可得，均衡点[E1]的特征值均小于零，[E2]、[E3]、[E4]、[E5]、[E7]均有非负特征值，即均衡点[E1]为本文渐进稳定点（ESS），点[E2]、[E3]、[E4]、[E5]、[E7]不能为本文渐进稳定点。

若[E6]为本文的渐进稳定点（ESS），则[Ca-Ka-La-Ra<0]且[Ii-Cb+Kb<0]，即投资者信息识别支出成本大于投资者的投资收益与额外收益之和，且政府采用补贴策略时政府的支出成本小于政府采用补贴策略时政府的基本收益、额外收益与间接损失之和，此时，政府采用补贴策略，科技型中小企业采用培育策略，而投资者采用不投资策略;若[E8]为本文的渐进稳定点（ESS），则[Ca-Ka-La-Ra<0]且[Ii-Cb+Kb>0]，即投资者信息识别支出成本小于投资者的投资收益与额外收益之和，且政府采用补贴策略时政府的支出成本小于政府采用补贴策略时政府的基本收益、额外收益与间接损失之和，此时，政府采用补贴策略，投资者采用投资策略，科技型中小企业采用培育策略。

五、 基于演化博弈的系统动力学模型仿真分析

1. 系统动力学模型构建

系统动力学是以系统内部各要素之间的因果反馈为基础，通过计算机模拟仿真技术，对系统动态行为演变进行定性和定量研究的应用学科。系统动力学方法所涉及的动态演变、因果关系、系统反馈等特征有助于研究分析系统内各主体行为决策动态变化过程，而且也可以通过调整参数探究仿真过程趋势变化。因此本文借助Vensim软件，构建了政府、投资者和科技型中小企业三方利益主体行为决策的系统动力学模型，该模型包括3个流位变量、3个流率变量、6个辅助变量、15个常量，如图1所示。

2. 模型检验

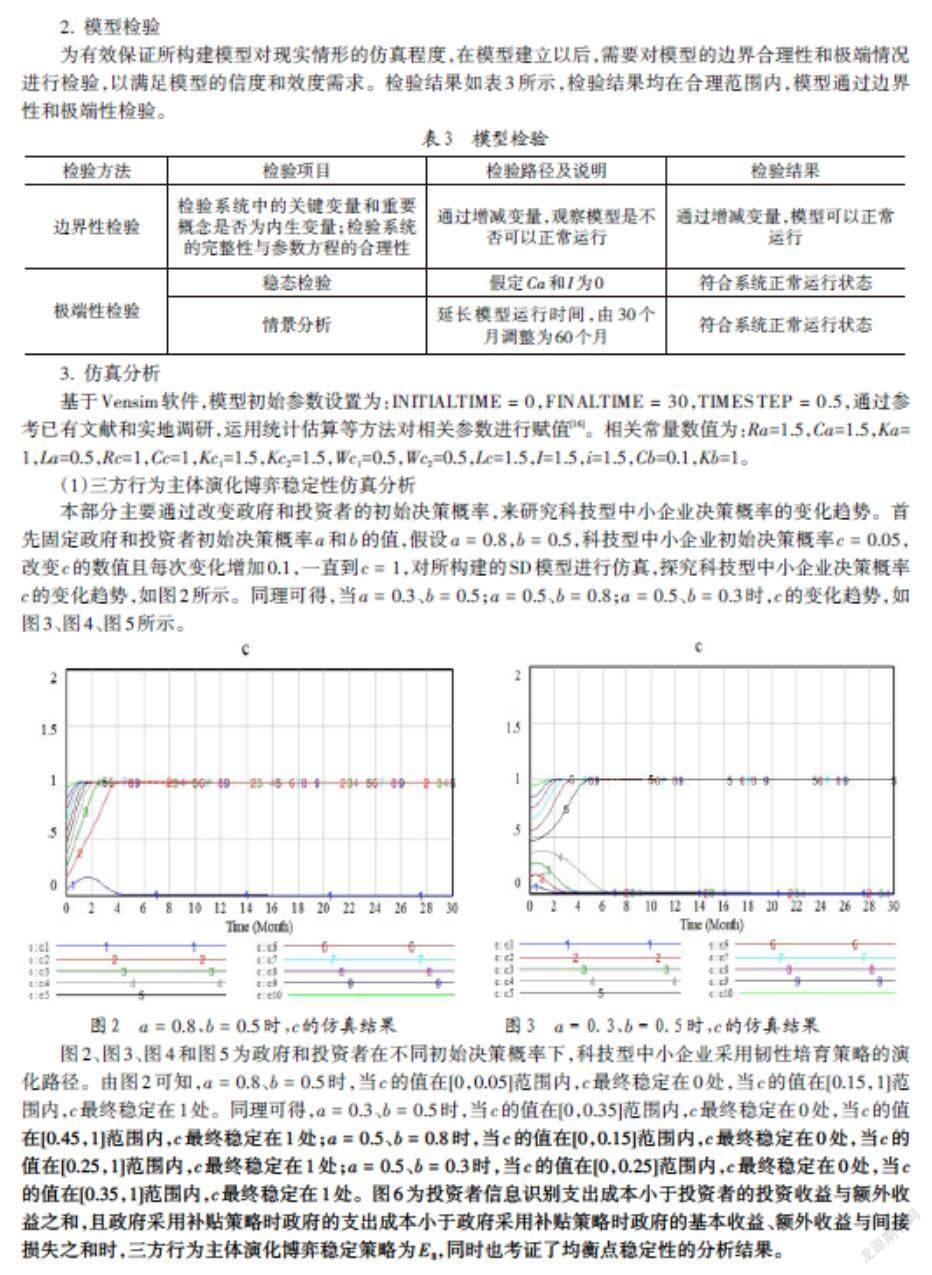
为有效保证所构建模型对现实情形的仿真程度，在模型建立以后，需要对模型的边界合理性和极端情况进行检验，以满足模型的信度和效度需求。检验结果如表3所示，检验结果均在合理范围内，模型通过边界性和极端性检验。

3. 仿真分析

基于Vensim软件，模型初始参数设置为：[INITIALTIME=0]，[FINALTIME=30]，[TIMESTEP=0.5]，通过参考已有文献和实地调研，运用统计估算等方法对相关参数进行赋值[16]。相关常量数值为：Ra=1.5，Ca=1.5，Ka=1，La=0.5，Rc=1，Cc=1，Kc1=1.5，Kc2=1.5，Wc1=0.5，Wc2=0.5，Lc=1.5，I=1.5，i=1.5，Cb=0.1，Kb=1。

（1）三方行为主体演化博弈稳定性仿真分析

本部分主要通过改变政府和投资者的初始决策概率，来研究科技型中小企业决策概率的变化趋势。首先固定政府和投资者初始决策概率[a]和[b]的值，假设[a=0.8]，[b=0.5]，科技型中小企业初始决策概率[c=0.05]，改变[c]的数值且每次变化增加0.1，一直到[c=1]，对所构建的SD模型进行仿真，探究科技型中小企业决策概率[c]的变化趋势，如图2所示。同理可得，当[a=0.3]、[b=0.5];[a=0.5]、[b=0.8];[a=0.5]、[b=0.3]时，[c]的变化趋势，如图3、图4、图5所示。

图2、图3、图4和图5为政府和投资者在不同初始决策概率下，科技型中小企业采用韧性培育策略的演化路径。由图2可知，[a=0.8]、[b=0.5]时，当[c]的值在[0，0.05]范围内，[c]最终稳定在0处，当[c]的值在[0.15，1]范围内，[c]最終稳定在1处。同理可得，[a=0.3]、[b=0.5]时，当[c]的值在[0，0.35]范围内，[c]最终稳定在0处，当[c]的值在[0.45，1]范围内，[c]最终稳定在1处;[a=0.5]、[b=0.8]时，当[c]的值在[0，0.15]范围内，[c]最终稳定在0处，当[c]的值在[0.25，1]范围内，[c]最终稳定在1处;[a=0.5]、[b=0.3]时，当[c]的值在[0，0.25]范围内，[c]最终稳定在0处，当[c]的值在[0.35，1]范围内，[c]最终稳定在1处。图6为投资者信息识别支出成本小于投资者的投资收益与额外收益之和，且政府采用补贴策略时政府的支出成本小于政府采用补贴策略时政府的基本收益、额外收益与间接损失之和时，三方行为主体演化博弈稳定策略为[E8]，同时也考证了均衡点稳定性的分析结果。

综上，政府和投资者初始决策概率越大，科技型中小企业越倾向于采用培育韧性策略。不同的初始决策概率使得科技型中小企业韧性培育策略的收敛路径有所不同，政府和投资者的初始决策概率越大，曲线收敛速度越快，即科技型中小企业决策越倾向于采用培育韧性策略。

（2）政府支出成本[Ca]对科技型中小企业决策概率的影响

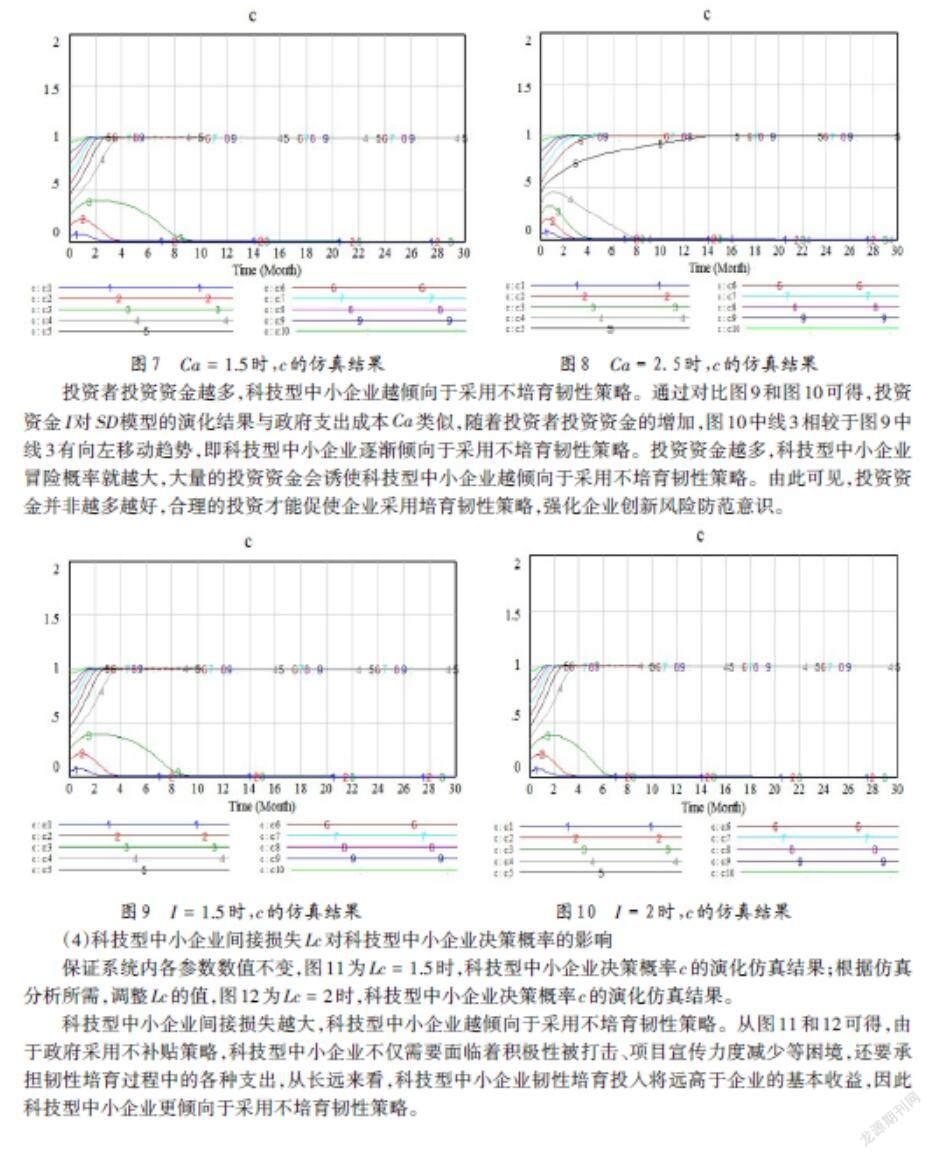
保证系统内各参数数值不变，图7为[Ca=1.5]时，科技型中小企业决策概率[c]的演化仿真结果;根据仿真分析所需，调整[Ca]的值，图8为[Ca=2.5]时，科技型中小企业决策概率[c]的演化仿真结果。

政府支出成本越高，科技型中小企业越倾向于采用不培育韧性策略。即随着政府加大对企业各项补贴的支出，政府财政压力逐渐增大，在收益变化较小的情形下，政府最终会采用不补贴策略。通过对比图7和图8可得，随着政府补贴的不断加大，科技型中小企业在初始阶段虽然可以得到大量补贴支持以应对企业经营过程中的各种创新风险，但过多的政府补贴会导致科技型中小企业滋生惰性，甚至为了满足补贴条件，以低质量产品应对政府政策，使得政府无法使用企业创新成果，最终双方归于不补贴、不培育的演化结果。

（3）投资者投资资金[I]对科技型中小企业决策概率的影响

保证系统内各参数数值不变，图9为[I=1.5]时，科技型中小企业决策概率[c]的演化仿真结果;根据仿真分析所需，调整[I]的值，图10为[I=2]时，科技型中小企业决策概率[c]的演化仿真结果。

投资者投资资金越多，科技型中小企业越倾向于采用不培育韧性策略。通过对比图9和图10可得，投资资金I对SD模型的演化结果与政府支出成本[Ca]类似，随着投资者投资资金的增加，图10中线3相较于图9中线3有向左移动趋势，即科技型中小企业逐渐倾向于采用不培育韧性策略。投资资金越多，科技型中小企业冒险概率就越大，大量的投资资金会诱使科技型中小企业越倾向于采用不培育韧性策略。由此可见，投资资金并非越多越好，合理的投资才能促使企业采用培育韧性策略，强化企业创新风险防范意识。<E：＼2022-1＼图片＼企业-3-5.png>

（4）科技型中小企业间接损失[Lc]对科技型中小企业决策概率的影响

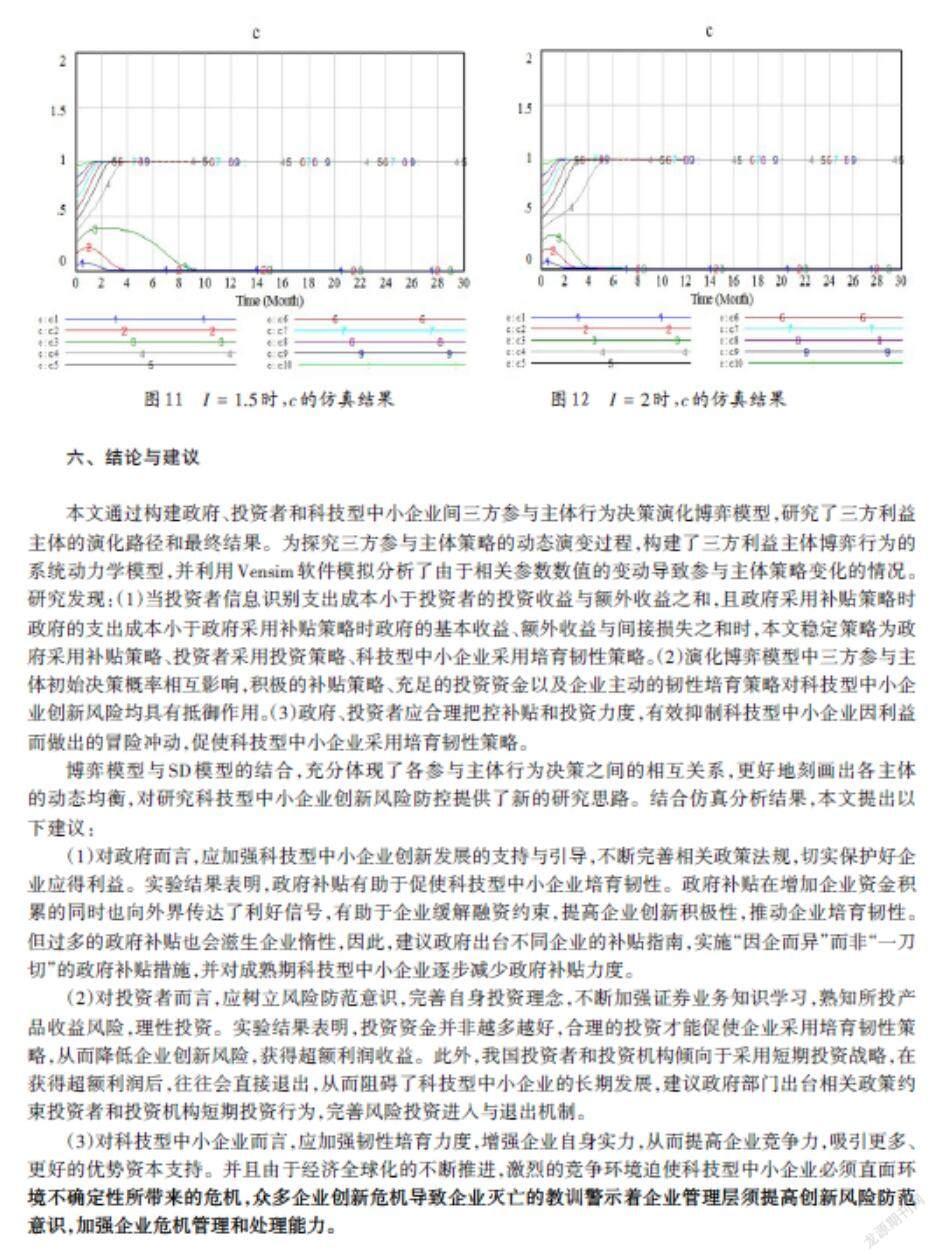
保证系统内各参数数值不变，图11为[Lc=1.5]时，科技型中小企业决策概率[c]的演化仿真结果;根据仿真分析所需，调整[Lc]的值，图12为[Lc=2]时，科技型中小企业决策概率[c]的演化仿真结果。

科技型中小企业间接损失越大，科技型中小企业越倾向于采用不培育韧性策略。从图11和12可得，由于政府采用不补贴策略，科技型中小企业不仅需要面临着积极性被打击、项目宣传力度减少等困境，还要承担韧性培育过程中的各种支出，从长远来看，科技型中小企业韧性培育投入将远高于企业的基本收益，因此科技型中小企业更倾向于采用不培育韧性策略。

z

六、 结论与建议

本文通过构建政府、投资者和科技型中小企业间三方参与主体行为决策演化博弈模型，研究了三方利益主体的演化路径和最终结果。为探究三方参与主体策略的动态演变过程，构建了三方利益主体博弈行为的系统动力学模型，并利用Vensim软件模拟分析了由于相关参数数值的变动导致参与主体策略变化的情况。研究发现：（1）当投资者信息识别支出成本小于投资者的投资收益与额外收益之和，且政府采用补贴策略时政府的支出成本小于政府采用补贴策略时政府的基本收益、额外收益与间接损失之和时，本文稳定策略为政府采用补贴策略、投资者采用投资策略、科技型中小企业采用培育韧性策略。（2）演化博弈模型中三方参与主体初始决策概率相互影响，积极的补贴策略、充足的投资资金以及企业主动的韧性培育策略对科技型中小企业创新风险均具有抵御作用。（3）政府、投资者应合理把控补贴和投资力度，有效抑制科技型中小企业因利益而做出的冒险冲动，促使科技型中小企业采用培育韧性策略。

博弈模型与SD模型的结合，充分体现了各参与主体行为决策之间的相互关系，更好地刻画出各主体的动态均衡，对研究科技型中小企业创新风险防控提供了新的研究思路。结合仿真分析结果，本文提出以下建议：

（1）对政府而言，应加强科技型中小企业创新发展的支持与引导，不断完善相关政策法规，切实保护好企业应得利益。实验结果表明，政府补贴有助于促使科技型中小企业培育韧性。政府补贴在增加企业资金积累的同时也向外界传达了利好信号，有助于企业缓解融资约束，提高企业创新积极性，推动企业培育韧性。但过多的政府补贴也会滋生企业惰性，因此，建议政府出台不同企业的补贴指南，实施“因企而异”而非“一刀切”的政府补贴措施，并对成熟期科技型中小企业逐步减少政府补贴力度。

（2）对投资者而言，应树立风险防范意识，完善自身投资理念，不断加强证券业务知识学习，熟知所投产品收益风险，理性投资。实验结果表明，投资资金并非越多越好，合理的投资才能促使企业采用培育韧性策略，从而降低企业创新风险，获得超额利润收益。此外，我国投资者和投资机构倾向于采用短期投资战略，在获得超额利润后，往往会直接退出，从而阻碍了科技型中小企业的长期发展，建议政府部门出台相关政策约束投资者和投资机构短期投资行为，完善风险投资进入与退出机制。

（3）对科技型中小企业而言，应加强韧性培育力度，增强企业自身实力，从而提高企业竞争力，吸引更多、更好的优势资本支持。并且由于经济全球化的不断推进，激烈的竞争环境迫使科技型中小企业必须直面环境不确定性所带来的危机，众多企业创新危机导致企业灭亡的教训警示着企业管理层须提高创新风险防范意识，加强企业危机管理和处理能力。

参考文献：

[1] 刘志坚.金融科技报告——行业发展与法律前沿[M].北京：法律出版社，2017.

[2] 许玲玲.高新技术企业认定、政治关联与民营企业技术创新[J].管理评论，2017，29（9）：84-94.

[3] 陈红川.高新技术企业技术创新风险管理决策研究[J].经济管理，2008（16）：91-96.

[4] Ishak A W， Williams E A. A Dynamic Model of Organizational Resilience： Adaptive and Anchored Approaches[J].Corporate Communications：An International Journal，2018，23（4）：00-00.

[5] 张公一，张畅，刘晚晴.化危为安：组织韧性研究述评与展望[J].经济管理，2020，42（10）：192-208.

[6] 吉云.风险投资进入能提升创业型企业的创新绩效吗？[J].科学学与科学技术管理，2021，42（5）.

[7] 夏清华，乐毅.风险投资促进了中国企业的技术创新吗？[J].科研管理，2021，42（7）：189-199.

[8] 苟燕楠，董静.风险投资进入时机对企业技术创新的影响研究[J].中国软科学，2013（3）.

[9] 朱庆华，窦一杰.基于政府补贴分析的绿色供应链管理博弈模型[J].管理科学学报，2011，14（6）：86-95.

[10] 卢现祥，李磊.企业创新影响因素及其作用机制： 述评与展望[J].经济学家，2021（7）：55-62.

[11] 王刚刚，谢富纪，贾友.R&D补贴政策激励机制的重新审视——基于外部融资激励机制的考察[J].中国工业经济，2017（2）：60-78.

[12] 夏清华，乐毅.风险投资促进了中国企业的技术创新吗？[J].科研管理，2021，42（7）：189-199.

[13] Keuschnigg C， Nielsen S B. Start-ups， Venture Capitalists， and the Capital Gains Tax[J].Journal of Public Economics，2002，88（5）：1011-1042.

[14] 张振刚，姚聪，余传鹏.管理创新实施对中小企业成长的“双刃剑”作用[J].科学学研究，2018，36（7）： 1325-1333.

[15] 田應东，杨文胜，王亚萌，等.电子优惠券营销市场参与主体决策行为演化博弈研究[J].软科学， 2020，34（8）：123-132.

[16] 张莉，杨栩，柯丽丽.政府扶持中小企业科技创新的动态演化博弈及仿真分析[J].科技管理研究， 2017，37（12）：15-23.

基金项目：国家社会科学基金一般项目“集成电路产业集群韧性测度、影响因素与提升路径研究”（项目编号：21BJY020）。

作者简介：赵伟（1995-），男，南京工业大学经济与管理学院硕士研究生，研究方向为企业战略管理;吴松强（1975-），男，南京工业大学经济与管理学院副院长、教授、硕士生导师，研究方向为产业创新与制造业转型升级;吴琨（1970-），女，南京工业大学经济与管理学院教授、硕士生导师，研究方向为企业战略管理。

（收稿日期：2021-11-08  责任编辑：殷 俊）