隐含波动率反演的改进高斯牛顿法

袁敬岚，江嘉华，何佳滨，邓小毛

摘要：隐含波动率是将市场期权价格代入Black-Scholes方程等期权定价模型反推得到的波动率结果，它反映投资者对未来一段时间内标的资产价格的波动程度的预期。牛顿迭代法、二分法等经典算法计算隐含波动率时，在部分数据上无法收敛．因此该文基于高斯牛顿法，提出一种隐含波动率的改进算法，利用L曲线法进行正则化参数选取及最小残差准则确定最优下降步长．使用上证50ETF期权数据的实验结果表明，本文提出的改进算法在数据集上可全部收敛，且可反演得到合理的隐含波动率。

关键词：隐含波动率；Black-Scholes 方程；高斯牛顿法；L曲线法

中图分类号：65F22， 68T05      文献标识码：A

文章编号：1009-3044（2022）33-0104-04

1 引言

金融衍生物是投资者用以风险管理的工具，期权就属于种类众多的金融衍生物中的一种．期权的发行者和持有者都希望以公平合理的价格进行交易，这就是期权定价问题．关于现代期权定价问题的研究，最早于1900年法国数学家Louis Bachelier在其博士论文《投资理论 （The Theory of Speculation）》中，从随机过程理论的角度研究资产价格，假设股票价格变化过程是一个布朗运动，首次提出了欧式看涨期权的定价公式．在Bachelier之后，期权定价理论开始蓬勃发展。1973年，Fischer Black和Myron Scholes建立了著名的Black-Scholes期权定价模型[1]，这一模型具有重大的意义。几乎在同时Robert Merton也发现了同样的公式并发表，同时做了推广应用的相关研究。

期权定价反问题也是期权领域的重要课题，其中一个为对隐含波动率的反演[2]。隐含波动率可以反映市场对标的资产包括股票、大宗商品、债券、货币等价格波动的预期，包含了未来波动率的信息。通过编制隐含波动率指数、隐含波动率曲面等方法可以与实际波动率比较，从而可制定基于波动率的风险溢酬的相关交易策略[3]。将市场期权价格等条件代入期权定价模型后可反推出隐含波动率，但是由于期权定价模型的复杂性，隐含波动率的计算通常不存在解析解。隐含波动率的计算方法主要分为近似解和数值解两类。在近似解方面，通过将正态分布进行泰勒展开，并做二阶近似可求解得到Corrado-Miller公式及其改进公式[4]；在数值解方面，从数值逼近的角度，若基于泰勒展开式可算得隐含波动率的无穷级数形式，通过计算系数得到其近似解[5]；此外基于Dirac Delta示性函数可得到隐含波动率的积分逼近形式，然后使用数值积分得到隐含波动率的渐进解[6] 。从最优化的角度，可以将Black-Scholes公式转化为一个最小二乘目标函数，然后使用牛顿法和二分法等最优化方法迭代求解，得到该优化问题所对应的隐含波动率[7] 。值得注意的是，经典牛顿法及二分法应用于实际期权数据时，常出现收敛较慢或者对部分数据无法收敛的情况，难以得到合理的结果。为此本文将基于Black-Scholes模型研究隐含波动率改进的计算方法。

本文选择上证50ETF期权数据作为实验数据计算隐含波动率。2015年，上证50ETF期权经过证监会批准后，在上海交易所上市，这是我国第一只ETF期权[8]。上证50ETF期权同时也是除铜期权外目前在我国上市交易的两种欧式期权之一。自从上证50ETF期权推出以来，受到投资者踊跃参与，一直有着良好的发展态势，对我国的衍生品市场乃至金融业都有积极的影响。我国的期权市场与国外期权市场相比起步较晚，现在仍处于萌芽阶段，随着我国期权市场不断完善成熟，可预见期权市场将有着可观的发展空间。因此对期权隐含波动率的研究不仅有学术价值，也具有现实意义。

2 Black-Scholes期权定价模型

在无税收、红利和交易成本，市场无卖空限制、交易连续进行、贴现率与无风险利率相等等假设下，欧式期权价格[Vt]满足如下Black-Scholes方程：

[∂Vt∂t+rSt∂Vt∂St+12σ2St2∂2Vt∂St2-rVt=0] （1）

其中[St]和[K]分别为股票价格和期权执行价，[r]为连续复利的无风险利率，[σ]为隐含波动率。[T]为期权有效期限，[t]为期权期限内某一时间，则[T-t]为期权剩余有效时间。边界条件为：

[hST=ST-K+，看涨期权K-ST+，看跌期权]  （2）

在风险中性的条件下，不难解得欧式看涨期权的定价公式为[9]：

[C=SNd1-Ke-rT-tNd2]   （3）

歐式看跌期权的定价公式为：

[C=Ke-rT-tN-d2-SN-d1] （4）

其中：

[d1=lnSK+r+σ22T-tσT-t]，

[d2=lnSK+r-σ22T-tσT-t]，

且[Nd1、Nd2]都是服从标准正态分布的变量的概率分布函数。

3 改进的高斯牛顿迭代法

由于Black-Scholes公式的复杂性，隐含波动率[σ]不存在解析解，一般可以通过如牛顿迭代法、二分法等数值方法求出隐含波动率的近似解。下面以欧式看涨期权为例，简要说明牛顿迭代法的计算步骤。首先构造最小化目标函数[fσ;S，K，r，T，t]，它表示期权定价模型中的理论价格[Cσ]与实际期权市场价格[C]的差，简记为：

[fσ=Cσ-C=SNd1-Ke-rT-tNd2-C] （5）

则牛顿迭代法表达式为：

[σk+1=σk-fσkf'σk] （6）

令[τ=T-t]，不难推得[fσ]，即Vega值如下：

[fσ=∂Cσ∂σ=S∂Nd1∂d1∂d1∂σ-Ke-rτ∂Nd2∂d2∂d2∂σ =SN'd1τ12]

（7）

此外Matlab软件的Finance工具箱中也集成了基于Black-Scholes公式求解隐含波动率的函数BLSIMPV， 该函数使用其优化工具箱中fzero函数进行目标函数寻优。fzero函数使用了二分、割线和反二次插值等数值方法的组合。

牛顿法收敛速度快，但在计算隐含波动率时存在某些数据无法收敛的问题。因此本文在高斯牛顿法的基础上提出改进算法。设[σ=σ1，σ2，…，σnT]为未知参数向量，其分量[σi]表示第[i]（[i=1，2，…，n]）个日期对应的隐含波动率；基于Black-Scholes公式的理论期权价格为[Cσ=Cσ1，Cσ2，…，CσnT]，实际期权价格为[C=C1，C2，…，CnT]。高斯牛顿法基于最小二乘法建立目标函数，且由于隐含波动率的求解是病态反问题，需加入正则化项来提高解的适定性。为了便于计算，选择L2正则化项，则目标函数可表示为：

[Fσ=C-Cσ22+ασ22]      （8）

[其中α]为正则化参数。目标函数的解为：

[argminσi≥0Fσ]                              （9）

高斯牛顿迭代法的基本原理为首先对目标函数进行线性化近似处理。为此，假设[Cσ]可近似为[σ]的线性函数，则可表示为：

[Cσ≈Cσ0+J0Δσ]               （10）

其中，[σ0]是[σ]的n维初值向量；[Δσ=Δσ1，Δσ2，…，ΔσnT]是[σ]的修正方向向量；[J0]是n[×]n的雅可比矩阵，可使用式（7）求得。令线性误差方程为：

[VΔσ=Cσ-C=Cσ0+J0Δσ-C] （11）

取[VΔσ]的二范数后得到：

[VΔσTVΔσ=Cσ0+J0Δσ-CTCσ0+J0Δσ-C]

（12）

则线性近似下的目标函数可转化为：

F[Δσ=VΔσTVΔσ+αΔσTΔσ] （13）

进一步，令F[Δσ]关于[Δσ]的一阶偏导为0。

[∂FΔσ∂Δσ=2JT0VΔσ+2αΔσ=0n×1] （14）

可推得正则化后的解为：

[Δσ=JT0J0+αI-1JT0C-Cσ0]      （15）

由此构建高斯牛顿法的迭代公式为：对于[k=0，1，…，n]。

[σk+1=σk+λkΔσkΔσk=JTkJk+αI-1JTkC-Cσk]        （16）

[Jk]是第[k]步迭代的雅可比矩阵。

该迭代格式中有两个需要确定的参数，即为正则化参数<E：＼2022知网文件＼33＼7xs202233＼Image＼image57.png>和迭代步长<E：＼2022知网文件＼33＼7xs202233＼Image＼image58.png>。首先，正则化参数的选取会影響解的精度，过大则解不准确，过小则数值不稳定。正则化参数可以通过先验选取或者后验选取。先验选取依赖精确解的先验信息，但在实际应用中精确解的先验信息往往难以获得。后验选取的方法有很多，常用的方法有广义交叉验证（GCV）、L曲线法等[10-11]。L曲线法可用于线性最小二乘泛函中正则化参数的选取。它的基本思路是通过构造最小二乘残差范数与L2范数正则化项的变化曲线，通过找出曲线上曲率达到最大值的点，得到其对应的正则化参数[11]。由于高斯牛顿法已对目标函数进行了线性化处理，故可采用L曲线法确定正则化参数。由于高斯牛顿法对初值的依赖性较强，在首先使用L曲线法取得正则化参数[α]之后，使用（15）计算[Δσ]后可得到一个改进的初值[σ0]如下：

[σ0=σ0+Δσ]                         （17）

其次，在迭代过程中，步长[λk]也会对迭代结果产生影响。如果步长过小，则需要的迭代次数会增加，从而降低收敛速度；如果步长过大，则迭代结果会快速变化，容易导致无法收敛。本文使用最小残差步长准则确定迭代步长[12]。记第[k+1]次迭代的残差[rk+1]为：

[rk+1=Cσk+1-C]

[≈Cσk+Jkσk+1-σk-C]                           （18）

把高斯牛顿法计算的[σk+1]表达式代入（3.14）式，得到如下形式：

示为杀出，长对

[ rk+1=Cσk-C-Jkσk+Jkσk+λkJTkJk+αI-1JTkC-Cσk]

[=rk-λkJkJTkJk+αI-1JTkrk][≜rk-λkBkrk]     （19）

其中记[Bk≜JkJTkJk+αI-1JTk]。对第[k+1]次迭代，要使残差最小，即：

[argmin  Rλk=rk+122]                   （20）

对[Rλk]关于[λk]求导，并令其为零，有：

[  R'λk=2rTk+1⋅r'k+1λk]                   [ =2rk-λkBkrkT-Bkrk]  [=-2rkTBkrk+2λkBkrk22=0]                                  （21）

最后化簡可得到步长[λk]。 表达式为：

[λk=rkTBkrkBkrk22]                     （22）

综上所述，基于改进高斯牛顿法的隐含波动率计算方法具体步骤如下：

Step1： 给定隐含波动率初值[σ0]，对期权定价公式在[σ0]处做线性化处理；

Step2： 利用L曲线法确定正则化参数[α]，并用（17）式更新隐含波动率初值[σ0]；

对于 [k=1，…n，]和[σk]，给定误差限[ε]，

Step3： 使用（7）式计算[Jk]，根据最小残差步长准则（22）式得到步长[λk]，使用（16）式更新得到[σk+1]；

Step4： 若满足[σk-σk-12]<[ε]，则停止迭代，输出隐含波动率的求解结果；否则回到Step3，直至收敛准则被满足。

4 实证分析

平值期权的执行价格等于或最接近于市场期权价格。由于在平值附近的期权交易更加活跃，相比实值期权和虚值期权更能反映市场的真实情况，故本文选取的样本包含四个50ETF期权平值看涨期权合约，分别是2016年7月28日至2017年3月22日、2017年3月23日至2017年6月28日、2017年6月29日至2017年9月27日、2017年9月28日至2017年12月27日共347个交易日的期权收盘价[C]、标的资产价格[S]、执行价格[K]、期权合约剩余期限[τ]（计算时除以年交易日数进行年化处理），无风险利率[r]选择2017年所有中债国债1年期利率的均值0.0330。数据来源为Wind数据库，为便于展示，时间按日期顺序排列并从1至347进行编号，下列所有图的时间轴均以日期编号代替具体日期。

下面将使用50ETF期权数据进行隐含波动率反演。由于从实际期权数据中反演的隐含波动率没有真解，故主要对比计算期权价格与实际期权价格的误差。高斯牛顿法的初值在所有日期均设为[σn=0.3，]误差准则选取为[σk-σk-12<ε]，其中误差限选取为[ε=10-5]。 用L曲线法算得的最优的正则化参数为[α=0.1091]，见图1。

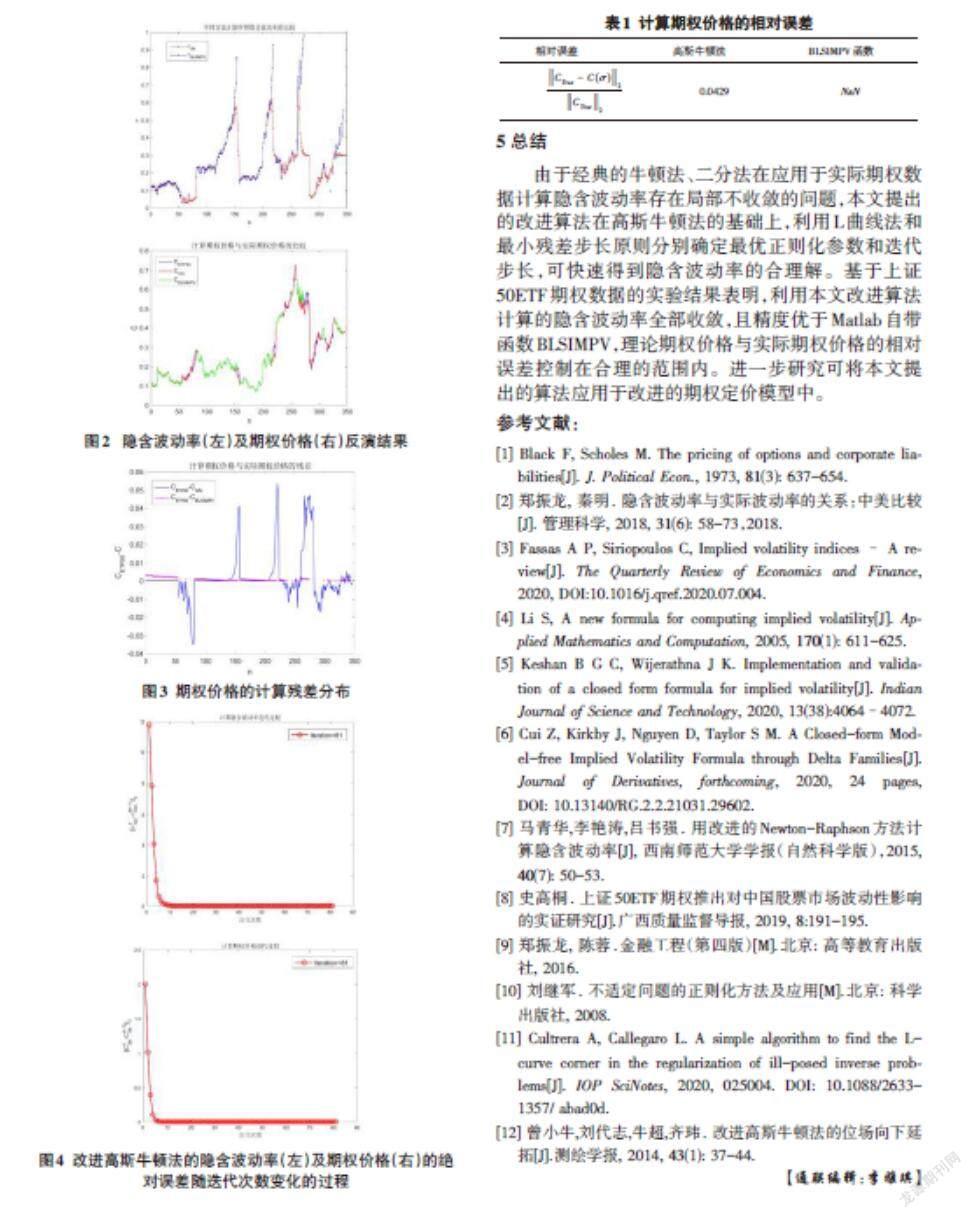
使用改进高斯牛顿法和Maltab软件中BLSIMPV函数算得的隐含波动率及期权价格的比较结果见图2-图4，期权价格相对误差见表1。由图2及表1可看出，改进高斯牛顿法对该数据集的所有数据均可收敛，计算期权价格与实际期权价格较为接近，其满足[Cσ-C<0.02]的数据点为311个，占比为[311347=89.63%] ；而BLSIMPV函数的计算结果中有98个数据无法收敛，显示结果为NaN，反演失败率为[98347=28.24%]。图3的计算残差分布显示，在BLSIMPV函数能收敛的点处，改进的高斯牛顿法的计算残差多位于零轴附近，比BLSIMPV函数的残差更小；在BLSIMPV函数无法收敛的数据点处，这些点多位于每两个期权数据的分界点附近，改进的高斯牛顿法均能收敛，且计算残差保持在合理的范围。图4中改进高斯牛顿法迭代过程显示其相邻两次迭代的绝对误差能快速下降，达到收敛准则的迭代次数为81次。由此知本文提出的计算方法对实际期权数据的隐含波动率反演更加有效，数值更加稳定。

5 总结

由于经典的牛顿法、二分法在应用于实际期权数据计算隐含波动率存在局部不收敛的问题，本文提出的改进算法在高斯牛顿法的基础上，利用L曲线法和最小残差步长原则分别确定最优正则化参数和迭代步长，可快速得到隐含波动率的合理解。基于上证50ETF期权数据的实验结果表明，利用本文改进算法计算的隐含波动率全部收敛，且精度优于Matlab自带函数BLSIMPV，理论期权价格与实际期权价格的相对误差控制在合理的范围内。进一步研究可将本文提出的算法应用于改进的期权定价模型中。

参考文献：

[1] Black F， Scholes M. The pricing of options and corporate liabilities[J]. J. Political Econ.， 1973， 81（3）： 637-654.

[2] 郑振龙， 秦明. 隐含波动率与实际波动率的关系：中美比较[J]. 管理科学， 2018， 31（6）： 58-73，2018.

[3] Fassas A P， Siriopoulos C， Implied volatility indices – A review[J]. The Quarterly Review of Economics and Finance， 2020， DOI：10.1016/j.qref.2020.07.004.

[4] Li S， A new formula for computing implied volatility[J]. Applied Mathematics and Computation， 2005， 170（1）： 611-625.

[5] Keshan B G C， Wijerathna J K. Implementation and validation of a closed form formula for implied volatility[J]. Indian Journal of Science and Technology， 2020， 13（38）：4064–4072.

[6] Cui Z， Kirkby J， Nguyen D， Taylor S M. A Closed-form Model-free Implied Volatility Formula through Delta Families[J]. Journal of Derivatives， forthcoming， 2020， 24 pages， DOI： 10.13140/RG.2.2.21031.29602.

[7] 马青华，李艳涛，吕书强. 用改进的Newton-Raphson方法计算隐含波动率[J]， 西南师范大学学报（自然科学版），2015， 40（7）： 50-53.

[8] 史高桐. 上证50ETF期权推出对中国股票市场波动性影响的实证研究[J].广西质量监督导报， 2019， 8：191-195.

[9] 郑振龙， 陈蓉.金融工程（第四版）[M].北京： 高等教育出版社， 2016.

[10] 刘继军. 不适定问题的正则化方法及应用[M].北京： 科学出版社， 2008.

[11] Cultrera A， Callegaro L. A simple algorithm to find the L-curve corner in the regularization of ill-posed inverse problems[J]. IOP SciNotes， 2020， 025004. DOI： 10.1088/2633-1357/ abad0d.

[12] 曾小牛，刘代志，牛超，齐玮. 改进高斯牛顿法的位场向下延拓[J].测绘学报， 2014， 43（1）： 37-44.

【通联编辑：李雅琪】