基于物元可拓模型的黄河兰州段突发水污染安全评价
崔文祥, 靳春玲, 贡 力, 刘晶晶, 苏 旸
(兰州交通大学 土木工程学院, 兰州 730070)
突发水污染指水体因固定污染源或移动污染源排放的污染物的介入,而引起水质变化,影响水的有效利用,危害人体健康或破坏生态环境的现象。近年来,伴随着经济快速增长,中国突发水污染事件频发。据统计,2014—2019年全国共发生突发环境事件1 900余起,其中生态环境部直接调度、指导处置的突发环境事件434起,水污染事件占60%左右[1]。2016年陕西省汉中市发生交通事故,30 t柴油泄漏流入嘉陵江支流,对该水源地居民饮水安全问题造成重大安全隐患;2017年汉中锌业铜矿违法加工并排放废水,导致嘉陵江广元段水质受到污染,铊浓度严重超标,对水源地水质安全造成了巨大影响[2]。因此建立科学、合理、有效的突发水污染评价指标体系及评价方法,对提高水环境风险应对能力、保障水生态环境安全具有重大意义。
针对突发水污染事件风险评价方面的研究,国内外专家、学者已取得了一定成果。国际上关于突发水污染风险评价的研究始于对海上溢油事故后果的定性评价,Canelas[3]首次对溢油事故风险状况进行了定性分析;Rebelo等[4]为向决策者评估污染风险提供技术支撑,提出了一种多准则概念模型;Fuhrer等[5]对因泄漏事故而存在于水体中的有毒化学物苯乙烯进行分析评价;国内的相关研究起始于2005年松花江重大突发水污染事件,如龙岩等[6]采用数据包络分析对突发水污染应急调控措施进行了探讨;练继建等[7]利用层次分析法构建了指标体系,对区域风险进行了分级;靳春玲等[8]通过研究流域突发水污染事故的特点及发生机理,从风险源、控制机制和风险受体出发,构建指标体系并进行黄河兰州段流域突发水污染风险评价;许静等[9]对流域突发水污染事件研发了一套快速模拟与预警系统;贡力等[10]引入ERG需求模型,构建幸福河评价指标体系,开展对幸福河(黄河兰州段)等级的定量评价。
总结前人研究发现,专家学者针对突发水污染的研究主要集中于风险识别和预警等方面,而对风险评价方面研究较少;传统的权重确定方法是将两种具有主观性和客观性的赋权方法组合,但过于主观或客观的方法在确定组合权重时并不能有效地避免误差产生。因此本文在明确界定突发水污染概念的基础上,运用压力—状态—响应(pressure-state-response, PRS)模型构建突发水污染风险评价指标体系,通过灰色关联分析法(grey relational analysis, GRA)和主成分分析法(principle component analysis, PCA)组合确定各指标权重,克服了主客观组合赋权法会产生误差的缺点,最后引入物元可拓模型,以黄河兰州段2014—2019年为例,分析得出其对应风险等级。对黄河兰州段的突发水污染安全等级划分,以期为黄河其他流域段全及国其他流域突发水污染风险的评价提供参考。
1 研究区概况及数据来源
黄河兰州段位于黄河上游,西起永靖县境内的刘家峡水库,东至景泰县的五佛寺,全长358 km。黄河从兰州市穿城而过,是兰州人民生活用水和工农业用水的重要水源,且城市人口密集、工矿产业众多导致了黄河水体脆弱性较强,其水质状况、水生态安全状况对兰州居民的健康及环境安全有着直接且重大影响。因此,对黄河兰州段进行突发水污染事故风险评价是必须且必要的。
本文在对黄河兰州段调研的基础上,通过查阅《中国水资源公报(2014—2019)》《甘肃省水资源公报(2014—2019)》《甘肃省统计年鉴(2014—2019)》《兰州市环境状况公报(2014—2019)》《兰州市统计年鉴(2014—2019)》及相关科研文献等方式获取数据资料。
2 研究方法
2.1 利用PSR模型构建指标体系
PSR模型[11]是20世纪80,90年代经济合作与发展组织(OECD)和联合国环境规划署(UNEP)提出,该模型针对:“压力—状态—响应”这一因果逻辑关系,反映了人类与社会之间的相互作用关系,可广泛应用于环境问题的相关研究[12-13]。如图1所示,通过对黄河兰州段的自然地理环境和社会经济状况调研,在遵循科学性、整体性、代表性、数据可获得性等指标体系构建原则基础上,从压力层、状态层、响应层3个层级综合确定指标体系,最终选取了人均水资源量、工业产值万元用水量、水质类别、城市人口密度、污水处理率、流域管理制度等16个相关指标构建了黄河兰州段突发水污染风险评价指标体系[14-15]。
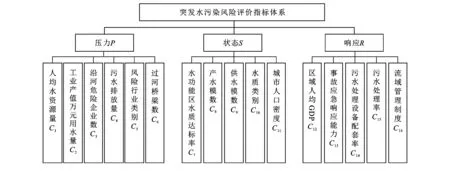
图1 黄河兰州段突发水污染安全评价指标体系
2.2 指标体系等级划分
根据《突发环境事件信息报告办法》《全国环境统计公报》《国家突发环境事件预案》以及相关文献资料[16-17],将突发水污染安全评价等级划分为4个等级,具体为:特别重大(Ⅰ级)、重大(Ⅱ级)、较大(Ⅲ级)、一般(Ⅳ级),各指标等级划分标准见表1。
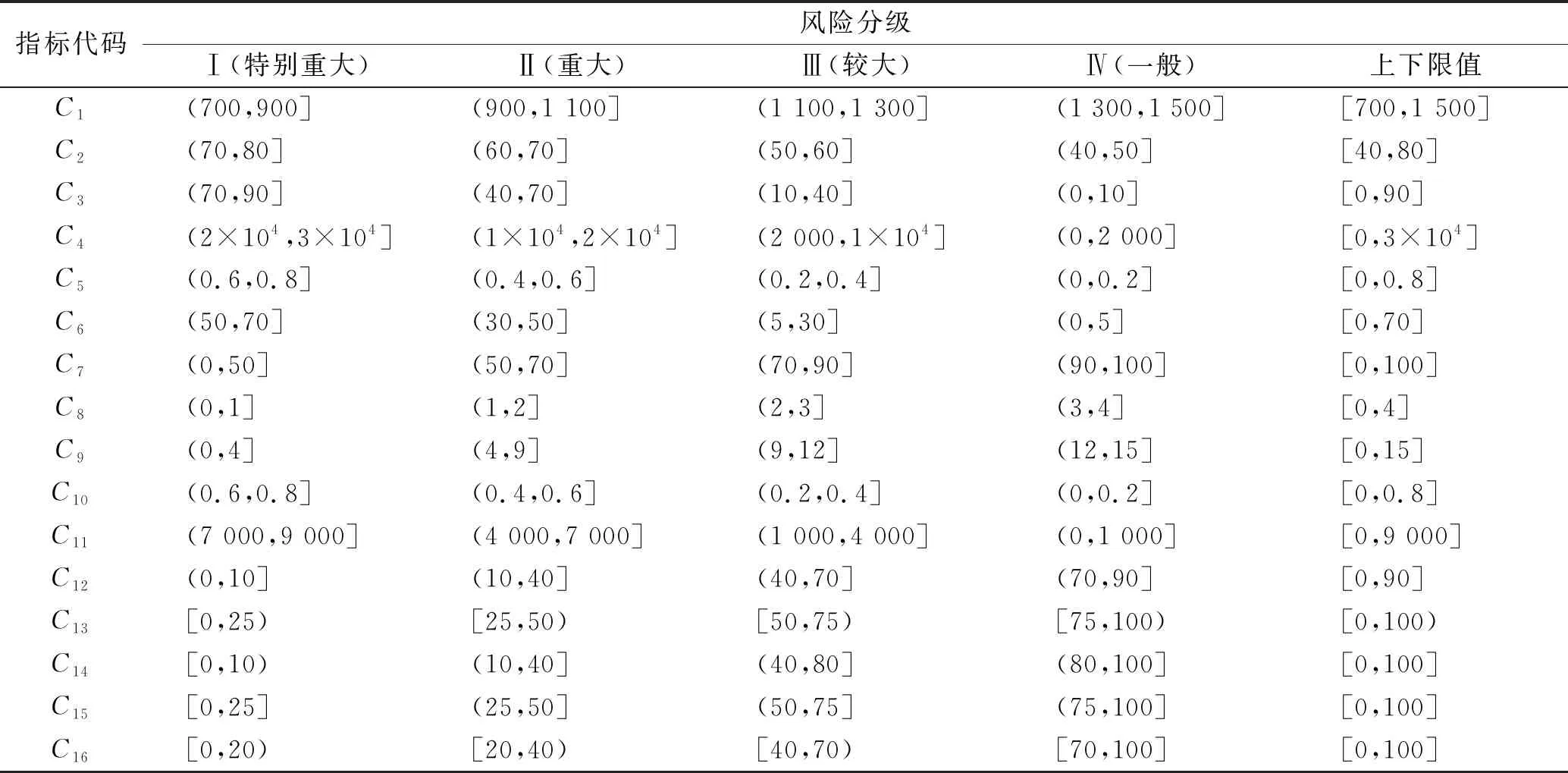
表1 黄河兰州段突发水污染安全评价指标体系划分
2.3 灰色关联分析法
灰色关联分析法(GRA)是基于邓聚龙教授提出的灰色理论基础上优化得到的一种多因素数据统计分析方法[18]。其根据序列对应指标之间变化趋势的相似性来判断序列的关联度,其具体步骤如下:
2.3.1 确定分析数列
①参考数列:反映各指标标准值的数据序列。
Y=Y(k)(k=1,2,…,n)
(1)
②比较数列:由各样本指标实际数据组成的数据序列。
Xi=Xi(k)(k=1,2,…,n;i=1,2,…,m)
(2)
2.3.2 变量归一化 为避免不同量纲带来的计算不便,需对指标数据进行规范化处理。
式中:k表示指标个数;i表示样本个数。
2.3.3 计算关联系数
ξik=
式中:ρ为分辨系数,表示两个数据序列在某个具体时刻关联度的大小。一般情况其值越小分辨力越佳,取值介于0到1较为合适,一般取值为0.5。
2.3.4 计算权重
2.4 主成分分析法确定权重
主成分分析法(PCA)是常用的线性降维数据处理方法,其主要思想是将原始数据中有一定相关性的变量重新组合成一组新的相互无关的综合变量来替代原始变量[19]。设该方法确定出的权重为W2,具体计算步骤如下:
(1) 假设存在m个待评对象,对每个待评对象有n个评价指标,组成一个m×n的数据分析矩阵Z。
式中:Zij为第i个待评对象的第j个指标,i=1,2,…,m;j=1,2,…,n。
(2) 对分析矩阵进行标准化处理并计算其相关系数矩阵R,通过解方程|λL-R|=0(L为特征向量矩阵),求出R的特征值及特征向量,其中特征向量为:λ1>λ2>…>λm,其对应的特征向量为:l1>l2>…>ln。
2.5 组合权重的确定
通过上述两种方法分别得到权重W1,W2。运用矩估计理论对以上两种权重结果进行组合赋权,既可以保持灰色关联分析法对指标客观描述的特点,同时可利用主成分分析法修正其对指标特点描述不强的缺陷[20]。
组合权重为:
W=αW1+βW2
(8)
式中:0≤W≤1,α+β=1。
又由于组合权重分别由上述两种的权重求得,则可计算出其对应的权重期望值为:
则有:
则α,β的表达式可写为:
根据公式(9)—(11)可得α=0.512 6,β=0.487 4,将系数和W1,W2代入公式(8)可得组合权重,具体为:W=0.512 6W1+0.487 4W2。
2.6 物元可拓模型
物元模型由20世纪80年代中国学者蔡文提出的可拓理论发展而来,其优于解决不相容的复杂问题,可从定性和定量两个角度进行分析,适合多因子评价[21-23]。突发水污染问题可以看做一个不相容问题,根据物元分析法构建突发水污染安全评价模型,具体步骤如下:
2.6.1 确定经典域、节域和评价物元 该理论以3个基本量组成一个有序组R=(N,C,V)来表征待评对象特征,其中N代表待评对象名称,C为对象指标值,V为指标等级划分区间。其中经典域表示为Rj:
式中:Rj为经典域,是由Nj,Cj,Vij组成的物元;Nj表示突发水污染安全等级的第j个等级,即为特别重大(Ⅰ级)、重大(Ⅱ级)、较大(Ⅲ级)、一般(Ⅳ级);Cj表示第j个等级Nj的特征,即指标因素;Vij表示第i个指标第j个分级取值范围,aij,bij分别表示各等级取值的上限值和下限值。
节域表示为RP:
式中:RP为节域,aij,bij分别表示各等级下指标的全部取值范围的上限值和下限值。
待测对象可以组成物元R:
式中:Vi为指标对应的实测值。
2.6.2 关联函数的计算 物元可拓的关联函数的值域为(-∞,+∞),极大地扩大了研究范围,可得到更多的分异信息;在等级确定上结合某些客观标准先对评价指标的经典域进行区间界定,之后通过各指标的关联函数计算得到其对应状态,最后利用模型集成得到所有指标的综合水平,提高了等级判定的客观性和科学性。
关联度K可以表示为:

式中:|Vji|=bij-aij。Kj(vi)代表各指标关联度。ρ(vi,Vji);ρ(vi,Vji)分别代表vi与有限区间Vji,Vpi的距离。
2.6.3 等级判断 综合关联度计算公式为:
式中:Kj(q)代表综合关联度;Wi为指标权重。
3 结果与分析
3.1 权重计算
参考相关科研文献及查阅2014—2019年公报年鉴,获取了16个突发水污染安全评价指标2014—2019年的详实数据,采用Matlab编程计算GRA权重W1,采用SPSS 22.0软件计算PCA权重W2,利用GRA-PCA组合赋权法确定各指标综合权重,具体结果见表2。
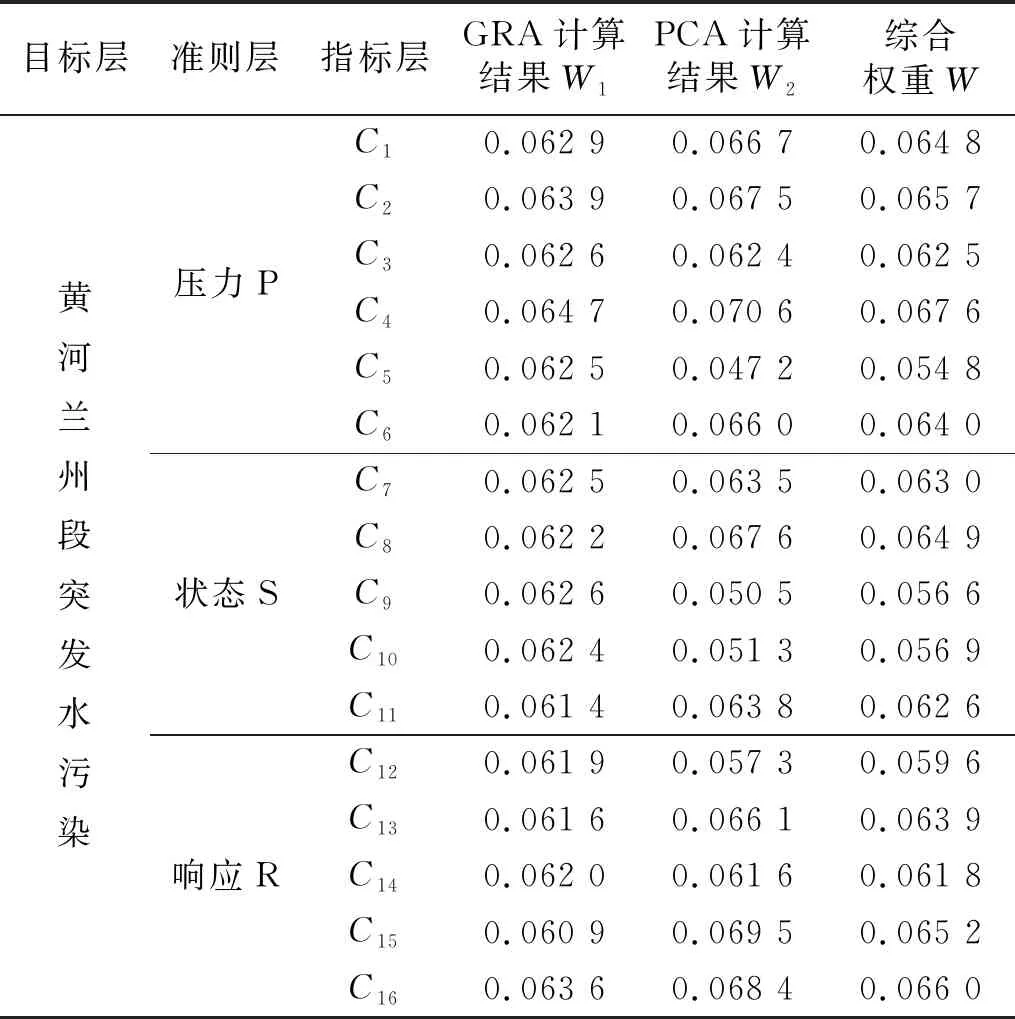
表2 黄河兰州段突发水污染安全评价指标体系及权重
3.2 模型评价过程
基于得到的权重计算结果,将其代入到物元可拓模型计算,步骤如下。
3.2.1 计算各指标关联度 将各指标2014—2019年对应数据代入物元可拓模型中计算,其中物元可拓模型通过Matlab编程实现,通过计算可得2014—2019年各指标对应的关联度,计算结果见表3。以2014年C1指标(人均水资源量)举例展示模型计算过程,将指标C1对应2014年数据v1=891代入式(12)—(16),可得该指标对应各评价等级的关联度分别为:k1(v1)=0.045,k2(v2)=-0.045,k3(v3)=-0.523,k4(v4)=-0.682,从而判定该指标安全等级为Ⅰ级,即属于“特别重大”水平。同理可得到其他指标对应关联度,鉴于篇幅所限,文中只列举了2014年各指标对应关联度,表3中列出了2014—2019年指标关联度确定的安全等级。
3.2.2 计算综合关联度 将得到的各项指标对应各等级的关联度(表3)与其对应的权重(表2)输入式(17)求出所有指标的综合关联度(表4),分别为k1(N2014)=-0.333,k2(N2014)=-0.112,k3(N2014)=0.126,k4(N2014)=-0.412。由此可判定2014年黄河兰州段突发水污染安全等级为Ⅱ级,即“重大”级别。同样的方法求得黄河兰州段2015—2019年突发水污染安全等级。
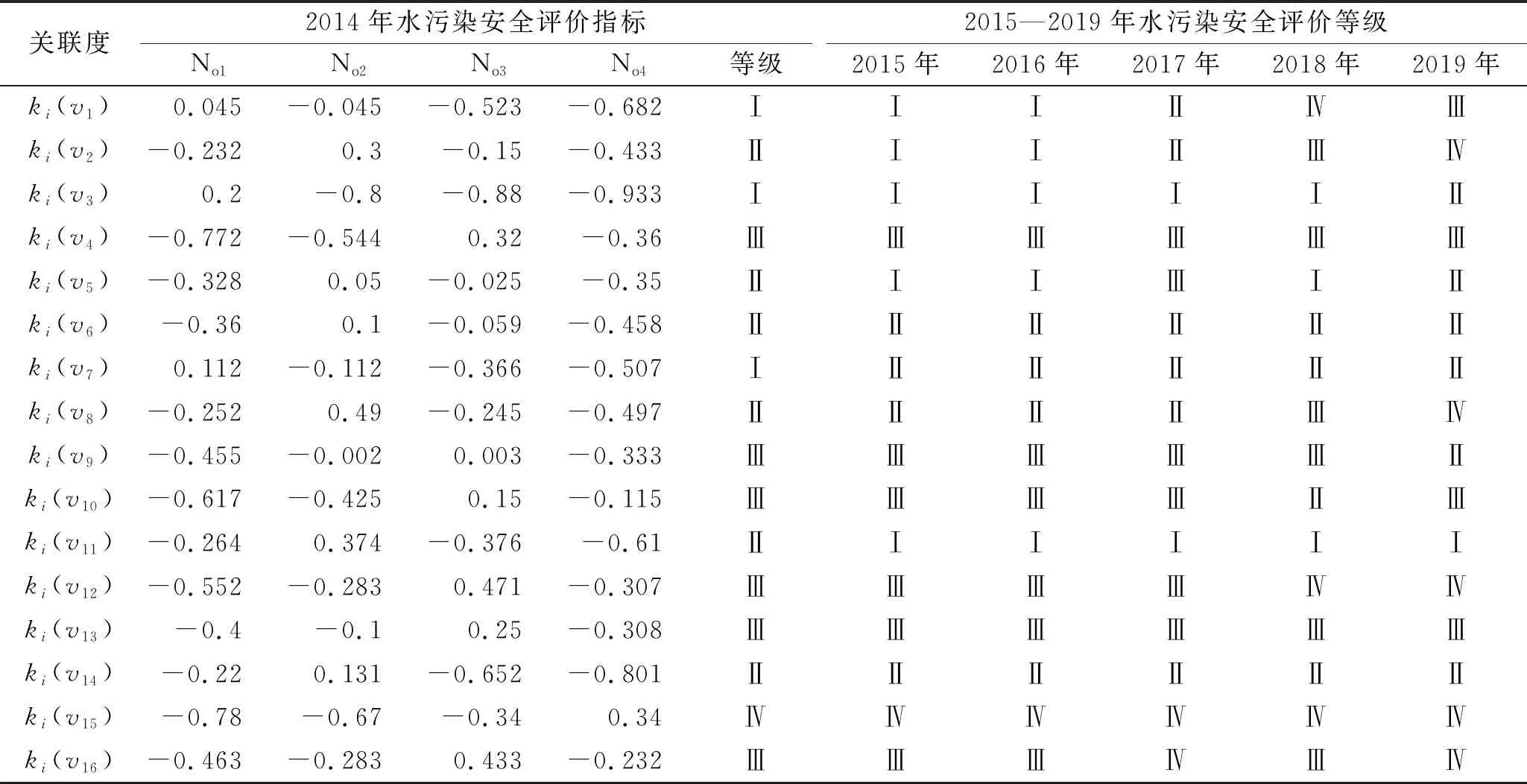
表3 黄河兰州段2014-2019年突发水污染安全评价指标关联度
由表4中可以看出,黄河兰州段突发水污染安全评价等级2014年为Ⅱ级(重大危险),2015,2017,2018年为Ⅲ级(较大危险),2016年为Ⅰ级(特别重大危险),2019年为Ⅳ级(一般危险);从时间顺序上来看,黄河兰州段突发水污染安全评价等级由Ⅱ级(重大危险)上升到Ⅳ级(一般危险),对应危险程度在逐年降低;对上表中得到的关联度确定的安全等级进行分析,可以看出,C4(污水排放量)、C13(事故应急响应能力)、C15(污水处理率)等指标对于当前年份安全等级的影响程度较大,而这些指标对应的安全等级多为Ⅲ级(较大危险)、Ⅳ级(一般危险),属于“良性”指标,从这些指标的实际意义出发可以反映出近年来关于黄河兰州段突发水污染状况在逐年改善;从上述分析可见,做好对污染源的排放质量的控制、加强对流域水安全相关制度的完善等措施对减少突发水污染影响具有非常显著的效果。2016年安全评价等级为Ⅰ级,2015,2017年均为Ⅲ级,但k1(N2016)=-0.241与k3(N2015)=-0.24非常相近,分析造成该年份安全评价等级与其他年份产生较大差异的原因是其他相关指标的片面性造成的,总体来看黄河兰州段突发水污染危险程度在逐年降低,水安全状况在逐年变好。
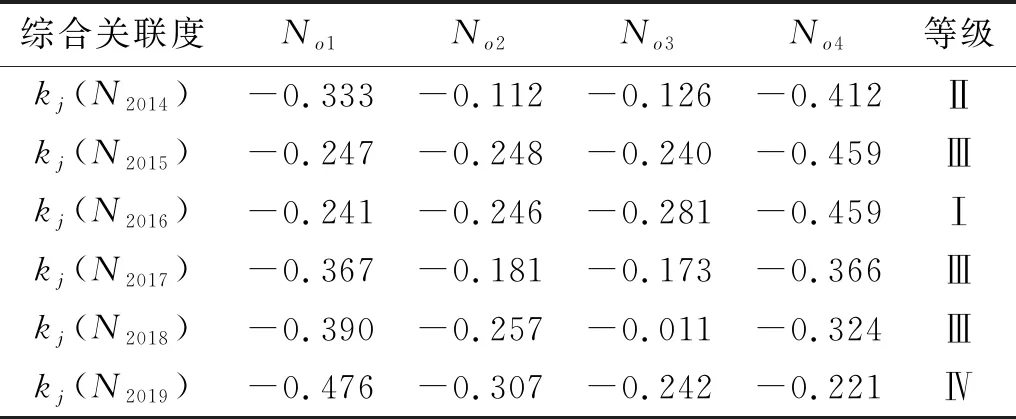
表4 黄河兰州段2014-2019年突发水污染安全等级对比
据滕汶瑾[25]在《筑牢生态安全屏障推动黄河兰州段生态保护和高质量发展》及王云祥[26]在《巧做山水文章筑牢生态屏障》中指出,截止2020年上半年,黄河兰州段干支流水质保持优良、出境水质评价稳定达到Ⅱ类、辖区内水质达标率及全市县级以上饮用水水源地水质达标率均为100%,以上报道也能对本研究结果的可靠性和准确性进行佐证。
4 结 论
(1) 为保证对黄河兰州段突发水污染安全评价的全面性、客观性、准确性,本文利用PSR模型建立评价指标体系,通过GRA-PCA组合赋权法确定各指标综合权重,考虑到突发水污染安全评价是一个复杂定性多指标评价,引入物元可拓模型建立黄河兰州段突发水污染安全评价模型,实现对黄河兰州段突发水污染安全的定量评价。
(2) 通过GRA-PCA组合赋权法确定各指标权重,利用物元可拓模型构建黄河兰州段突发水污染安全评价等级模型,计算得到黄河兰州段2014—2019年的突发水污染安全评价等级由Ⅱ级(较大危险)向Ⅳ级(一般危险)跃升,评价结果与近年来黄河兰州段突发水污染治理效果基本一致,这表明该模型对黄河兰州段突发水污染安全等级评价的结果合理可靠。
(3) 限于资料收集不够充分,本文只针对了黄河兰州段进行了模型的应用评价。研究表明,黄河兰州段突发水污染安全的评价结果是非常贴合实际的。鉴于本文研究实例隶属黄河流域范围,因此该模型可扩展应用于黄河其他流域段突发水污染评价,亦可为全国其他流域突发水污染风险的评价提供借鉴。

