兰勃特投影向高斯投影转换程序编制及难点分析

胡圣武 鞠全泰 张其华

(河南理工大学 测绘与国土信息工程学院 河南 焦作 454000)

0 引言

兰勃特(Lambert) 投影包括等角圆锥投影和等积方位投影,本文研究的兰勃特投影是指等角圆锥投影。兰勃特投影与高斯投影在我国应用非常广泛,我国规定大于等于1∶50万地图均采用高斯投影,据对高斯地图投影变形分析和地图精度的要求,我国规定比例尺大于和等于1∶100 000地图采用3°带投影,比例尺小于和等于1∶25 000地图采用6°带投影;而小于等于1∶100地图,大多采用等角圆锥投影即兰勃特投影[1-2]。由于二者均是我国地图投影的主要方式,因此,在实际应用中两者之间坐标的相互转换是常见问题[3-5]。

目前国内关于兰勃特投影和高斯投影的转换问题,主要分为数值法和解析法两种方法,其中解析法是地图投影转换的主流方法,它又分为正解析法和反解析法。

反解析法就是通过中间过渡的方法,反解大地经纬度坐标(B,L),在带入到新地图投影公式中求解其平面坐标的方法,即(x,y)→(B,L)→(X,Y)。对于以极坐标形式的投影,如圆锥投影,还需要以极坐标作为中间过渡。即(x,y)→(ρ,δ)→(B,L)→(X,Y)的方式进行转换[6]。这种转化方式不受区域范围的限制,在转换过程中,理论上不会存在精度损失。缺点就是计算过程复杂,计算量大。依赖于使用计算机进行数据计算[7]。

正解析法就是在复变函数理论的基础上,将某一点的两种投影的平面坐标作级数展开。通过计算机求解多项式的系数,从而得到两种等角投影平面坐标间的直接转换公式。正解析法的优点是不需要任何中间变量,可实现兰勃特投影向高斯投影平面坐标间的转换。不足之处则是转换的精度受转换的方式和展开的阶数有关,也受到转换区域大小的限制,转换区域越大精度越低[8-9]。

本文主要利用反解析法,即利用大地经纬度作为过渡,先将兰勃特投影平面坐标以极坐标的形式表示,再将其转换为大地经纬度坐标,最后再将大地经纬度坐标代入高斯正算公式转换为高斯平面坐标进而转换为通用坐标,并通过编程实现二者的转换,并分析了程序编制中的难点问题。

1 基本理论

1.1 兰勃特投影

兰勃特等角圆锥投影是J.H.兰勃特于1772年所创,根据其与旋转椭球面的交线个数不同,将其分为兰勃特切圆锥投影和兰勃特割圆锥投影[9-10]。圆锥面与旋转椭球的交线成为标准纬线。

兰勃特投影的坐标及变形计算一般公式为

(1)

式中,ρ为纬线投影半径;ρs为最低纬度的投影半径;B为纬度;ΔL是地球椭球面上两条经线的夹角;δ是两条经线夹角在平面上的投影;β是小于1的常数,在同一兰勃特投影中β是不变的,但在不同的兰勃特投影中β是变化的;m,n为经纬线长度比;a,b为极值长度比;ω为最大角度变形值;M是子午圈曲率半径;(x,y)是平面坐标。

1.2 高斯投影

在高斯投影的投影平面上,中央子午线和赤道的投影都是直线。在确定投影带之后,以任意带的中央经线的投影作为X轴,Y轴则是赤道在高斯投影面内的投影,交点O为坐标原点,如图1所示。高斯-克吕格投影的直角坐标公式为

图1 高斯投影示意图

(2)

式中,s为由赤道至纬度B的经线弧长;η=e2cosB;N为卯酉圈半径。特别要注意的是式中的L是经过中心化的经度值,不是原经度值。

1.3 两种投影转换实现过程

兰勃特投影向高斯投影转换流程如图2所示。

图2 兰勃特投影向高斯投影转换图

2 兰勃特投影向高斯投影转换的难点问题

2.1 如何从兰勃特投影的平面坐标(x,y)求其大地经纬度。

已知(x,y)求解大地坐标经纬度(B,L),其公式为

(3)

式中,ρ0为中心纬度的投影半径;l为经差;q为等量纬度;Δq为等量纬度差;ΔB为纬度差;b1,b2,b3,b4,b5与纬度有关的系数。从式(3)中不能求出纬度B。采用等量纬度反解大地纬度的方法来求解大地纬度B。

要想求解大地纬度B,首先要引入等量纬度q,即

(4)

把子午圈曲率半径M和卯酉圈曲率半径N带入式(4)可得

(5)

经过简单的数学变换可得等量纬度与大地纬度的关系式为

(6)

显然,当B=0°时,q=0。

如果令e1=0,则地球椭球体变为球体,椭球面大地纬度B变为球面纬度φ,则有

(7)

将上式积分上下限分别为B和B0,经过二次计算就可求得B和B0的等量为纬度q和q0。就可以得到由大地纬度计算等量纬度差Δq的公式。为方便实际计算,并不是采用式(7),而是直接采用大地纬度差ΔB来计算等量纬度差Δq的级数展开式[11-12]为

(8)

经过泰勒级数展开式(8)并设

(9)

则可得

(10)

逐次求导,可得

(11)

则可得

(12)

式中,

(13)

该方法可以简化ρ的计算,使之更容易被计算机实现。可得

(14)

2.2 在高斯正算公式中L的确定

知道了圆锥投影地图上每点的(B,L),则可按式(2)求出平面坐标。不过在代入公式之前要解决L的值的问题。在高斯正算中,每个点有两种坐标,即3°度带和6°度带。因此,要先求出每个带的中央经度。

3°度带带号n与相应的中央子午线经度L0的关系为

(15)

6°度带每带的中央经线度L0和代号n为

(16)

式中,[ ]表示商取整;L为某地点的经度。

根据式(15)和式(16)求出相应的中央经度L0,则式(2)中L为

(17)

根据式(2)求出的平面坐标,x坐标一定是正值,y坐标有正有负,这样的坐标称为自然坐标值。为了避免坐标出现负值,把y坐标进行了处理,即加上500 km再加上带号。这样的坐标称之为通用坐标。

3 利用C#实现兰勃特投影向高斯投影转换

3.1 兰勃特投影反算

其流程图如图3所示。

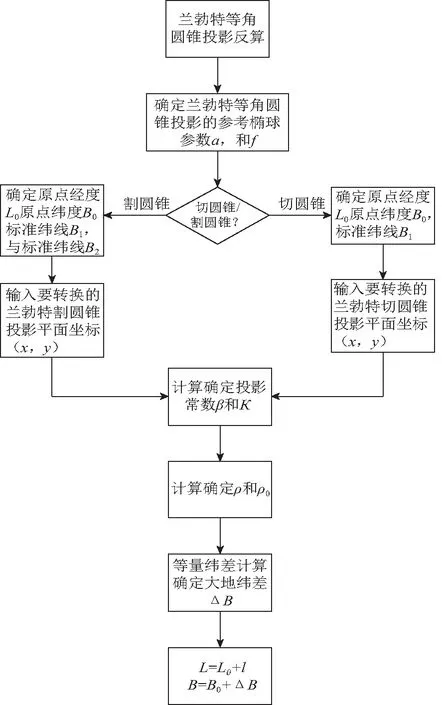
图3 兰勃特投影反算流程图

3.2 高斯投影正算

其流程图如图4所示。

图4 高斯投影正算流程图

3.3 程序界面

程序编写过程中,考虑到兰勃特切圆锥还是割圆锥的情况,通过单选框来让用户确认。程序默认了一些投影椭球参数,也给定了自定义椭球参数的选项,以便用户在不同参考椭球中都可以使用该程序进行坐标转换工作,如图5所示。

图5 测量程序界面

4 工程实例

在河南省区图中,取原点经度L0=113°30′,原点纬度B0=35°。由我国各省所选的两条标准纬线表可知,B1=32°30′,B2=35°30′。其兰勃特平面坐标为(3 021 513.241 9,978 993.339 4)参考椭球为1975国际椭球。通过本程序算得该点在3°带和6°带的坐标,如图6和图7所示。

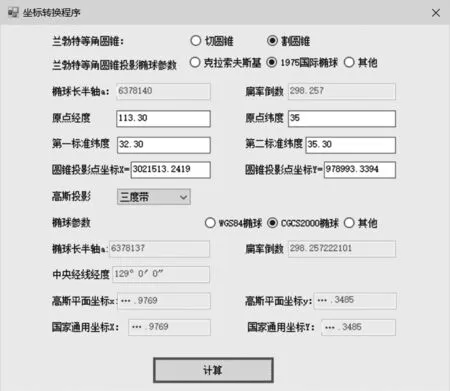
图6 三度带成果图

图7 六度带成果图

5 结束语

本文对兰勃特投影向高斯投影坐标转换进行了系统的理论分析和公式推导。本文应用C#语言编写出视窗体(WinForm)程序,可通过计算机进行两种投影的单点计算。在确定Lambert投影的投影方式(切圆锥还是割圆锥),及投影参数(原点经度和标准纬线纬度),通过计算即可求解得到该点在高斯投影当中的坐标和通用坐标。程序给出了3°带和6°带的选项,通过自主选择,可直接求得不同投影带之间的坐标。

程序编制的过程中,只给出了单点间的两种投影之间的转换,没有给出批量点的转换程序。