基于网络层加权的多层复杂网络社区检测算法

邰昌鸿，刘向阳

(河海大学 理学院，江苏 南京 211100)

0 引 言

多层网络是由多个图(称为层)组成的网络，这些图共享同一组节点，但它们的边不同。多层网络中的边缘被分为层内边和层间边。多层网络社区检测的研究方法主要可分为三大类：展平方法，将多层的信息折叠成单一层，再使用传统的单层算法检测社区。聚合方法，发现每一层中的社区，然后通过某种聚合机制将它们合并。直接方法，通过优化一些质量评估标准而不进行扁平化处理来直接检测多层网络上的社区结构[1]。

其中基于展平方法的代表算法MCD-Berlingerio[2]，设计了一个用于查找和表征多维社区的框架，该框架基于从多维网络到一维网络的映射，并基于现有的一维社区发现算法对其的应用，还可以恢复原来存在的多维社区结构；基于聚合方法的代表算法PMM[3]，主要可以分为两步：第一步是提取每层网络的模块度矩阵的特征向量并获得级联的向量，然后采用PCA(principal component analysis)得到一个较低维的嵌入，捕获网络所有维度(层)上的主模式；第二步是对所有节点的低维嵌入表示执行k-means算法，以找出离散的社区划分；基于直接方法的代表算法Gen Louvain(GL)[4]，使用多层切片模块扩展了经典的Louvain方法，因此每个节点层元组都分别分配给一个社区；多层局部社区检测算法ML-LCD[5]，在全局信息未知的情况下，通过优化局部社区函数(即内部链接密度和外部链接密度比)标识特定节点所在的社区，然后通过将特定层的贡献值与链接密度比进行线性组合将局部社区函数扩展到多层网络[6]。

但上述关于多层复杂网络全局或局部社区检测的算法，均忽略了复杂网络层与层之间的重要性差异，在真实的多层复杂网络中的节点往往并不是均匀分布在每一层中，而是往往存在多数层上包含较少的节点，而少数层却包含更多的节点的情况，例如航空网络中的昂贵航线与廉价航线的分布。因此当移除少数节点所在层时对网络结构的影响有限，但当多数节点层被移除时，就可能会造成网络的崩溃，这说明复杂网络层之间存在重要性差异；同时局部社区检测算法的效果多依赖于选取种子节点时其所处社区位置的好坏，当其位于社区核心时划分效果较好，反之则较差；为避免种子节点的随机性造成划分结果差距较大，该文提出一种新的局部社区检测算法MWLCD，对多层复杂网络层的重要性展开分析，定义了基于层内活跃节点占比及不同层包含重要节点占比两种层加权方案，并基于层加权引入局部密度在随机获取的种子节点确定其所在社区的核心节点，从而完成了多层模块度值更高且更加稳定的社区划分。

1 多层网络与社区检测ML-LCD算法

1.1 多层网络

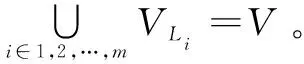
EL={(u,Li),(v,Lj)|u,v∈V∧Li,Lj∈L∧i=j}∪{(v,Li),(v,Lj)|u,v∈V∧Li,Lj∈L∧i≠j}

(1)

1.2 ML-LCD算法

Interdonato等人提出了第一种多层网络上的局部社区发现算法ML-LCD(multi-layer local community detection)[5]，并定义了多层局部社区检测问题。复杂网络图中的局部社区检测问题是指对特定于查询节点且依赖于有关网络结构的有限信息的社区的识别。局部社区检测算法通常实现某种策略，该策略在每个步骤考虑来自三个集合之一的节点，即：正在构建的社区(用种子节点初始化)节点集B、作为社区中节点的邻居但不属于该社区的外壳节点集S以及网络的未探索部分节点集[5]。ML-LCD算法定义了三层算法框架，分别是基于层加权的ML-LCD-lwsim和基于层内相似度的ML-LCD-wlsim以及层间相似度的ML-LCD-clsim。其中ML-LCD算法中的ML-LCD-wlsim和ML-LCD-clsim在性能上均低于ML-LCD-lwsim。

需要注意的是，虽然ML-LCD算法的第一层函数框架提到了层加权的概念，但该算法依然采用层均等权重划分的方式对网络层加权，即认为所有网络层重要性相同，或者需要预先设置权重值对特定网络加权，这与真实的网络的拓扑特征并不相符，也无法适用于大型网络的权重值衡量。

2 基于网络层加权的多层局部社区检测算法

2.1 MWLCD算法

基于ML-LCD算法第一层函数框架的层加权概念，该文提出了一种基于层加权的多层网络社区检测算法MWLCD。MWLCD算法量化了多层复杂网络的层权重值，并引入局部密度算法在随机获取的种子节点周围确定社区的核心节点，基于核心节点完成了模块度更高且更稳定的局部社区划分。该文的主要任务是如何量化网络层的权重值和确定核心节点，并基于核心节点选择外壳集S中的最佳节点来添加到要识别的社区中。社区C的外壳集定义为：

S={v∈VC|∃((u,Li),(v,Lj))∈

EL∧u∈C}

(2)

社区C的边界集定义为：

B={u∈C|∃((u,Li),(v,Lj))∈EL∧v∈S}

(3)

其中，Li与Lj可以为不同层，即B包含了耦合边的边界节点。

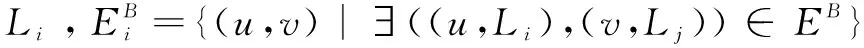
ML-LCD算法考虑要添加到正在构建的社区的候选节点与到社区内外部的节点链接的密度比作为惩罚函数[4,8-9]。在这项工作中，该文采用上述一般方法。

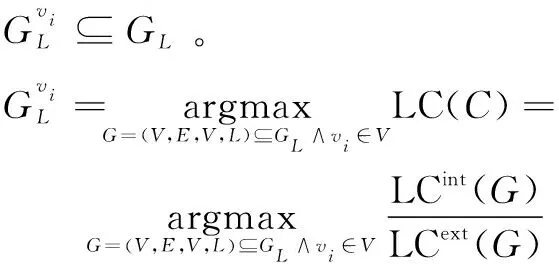
(4)

其中，LCint(G)是与G内节点之间的链路密度成正比的函数，LCext(G)是与G内节点与G外节点之间的链路密度成正比的函数。

给定GL=(VL,EL,V,L)和局部社区C，基于网络层加权的局部社区内部函数被定义为：

基于网络层加权的局部社区外部函数定义为：

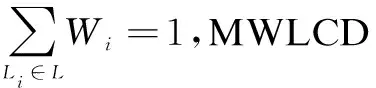
2.2 层加权

该文引入真实复杂网络层的重要性差异，通过量化和归一化处理，获得复杂网络各层的权重值。选取了两种加权方案结合的方法来适应不同拓扑结构的多层复杂网络。

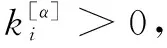
(7)

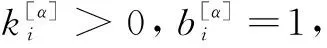
定义权重W1为：

(8)

(9)

第二种加权方案基于局部密度算法[11]。衡量不同网络层包含重要节点的占比。衡量该比值需要计算节点在每一层中的局部密度与偏移量，节点局部密度定义如下：

(10)

其中，dc为截断距离，是可变参数，实验中取所有节点之间距离的前2%，dij是节点之间的距离。

节点偏移量定义如下：

(11)

即对于非局部密度最大的点，计算δi值，主要分两步，找到所有局部密度比节点i高的节点；在这些点中找到距离节点i最近的节点j，节点i和j的距离就是δi的值。对于局部密度最大点，δi实际上是该点和其他所有节点距离值的最大值。

权重W2定义为：

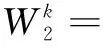
(12)

(13)

即计算每层中前n个局部密度值与偏移量乘积值最大的节点之和在所有层中的比值，再计算方差衡量层与层之间比值的波动情况，当方差超过设置的波动阈值s2(W2)=0.5时则表明层与层之间的波动值较大，此时应加大第二加权方案比重，否则加大第一加权方案比重。依据波动值变化对网络层加权的影响，该文设置了一个超参数k=0.999用于结合第一种加权方案与第二种加权方案，其定义如下：

W=kW1+(1-k)W2

(14)

其中，W代表层的综合权重，W1代表第一加权方案权重，W2代表第二加权方案权重，超参数将两种加权方案按方差波动变化是否超过阈值决定如何分配其占比。

2.3 核心节点计算

基于2.1节获取的网络层权重为节点多层链接加权，该文通过引入局部密度获取随机种子节点v0所在社区的核心节点集{vi|i=1&i=2}。具体工作如下：

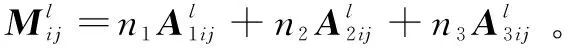
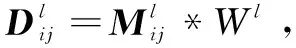
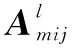
Step5:为防止搜索的核心节点位于不同社区造成两社区合并，该文将核心节点限制在彼此δ阶邻域范围内，并在实验中将核心节点数目取1至2个。

Step6:确定核心节点后，该文将外壳集中节点按到核心节点距离从小到大排序，按距离大小选择社区候选节点。

在第3章中将详细分析在不同的种子节点邻域内搜索核心节点的划分结果。

2.4 MWLCD算法步骤

MWLCD算法在局部社区划分初始阶段为网络层设置权重，并基于网络层加权获取任意选取的节点周围的社区核心节点，并依据社区核心节点获得局部社区划分。MWLCD算法步骤如下：

算法：基于网络层加权的多层复杂网络局部社区检测(MWLCD)算法。

输入：多层网络图GL=(VL,EL,V,L)(可以是局部图)及随机节点v0

输出：基于核心节点划分的社区集合

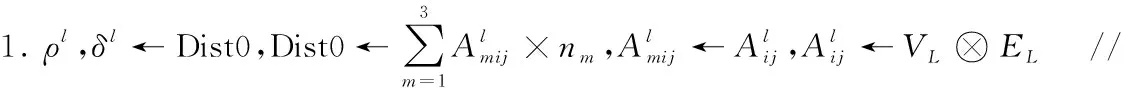
3.ifs2(W1)>0.5:k=0.999 else:k=0.001

4.W←k*W1+(1-k)*W2

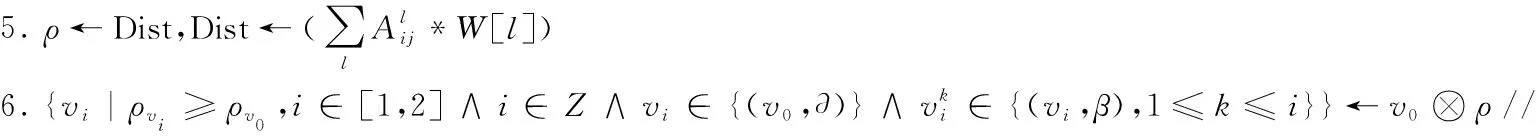
7.S←{v|(v,vi)∈El∀l∈L∧min(Dist(v,vi))},C←B,B←{vi}

8.currLCint←LCint(C),currLCext←LCext(C) //使用公式(5)及公式(6)

9.currLC=currLCint/currLCext

10.Repeat

11.S←S{v*},v*←argmaxv∈SLC(C∪{v})//找到使LC(C)值最大的候选节点v*

12.B←B{u∈B|v*∈N(u)Λ/∃(u,v):v∈S}

13.if LC(C∪{v*})>currLC∧LCint(C∪{v*})>currLCint←LCint(C)

14.N-C←N(v*)C,C←C∪{v*}

15.ifN-C≠φ

16.S←S∪N-C,B←B∪{v*}

17.B←B∪{u∈CB|N(u)⊆S}

18.currLC=currLCint/currLCext,currLCint←LCint(C),currLCext←LCext(C)

19.else

20.currLCext←LCext(C)

21.直到LC(C)值不再增大为止

22.returnC

步骤1～步骤6为MWLCD算法初始化阶段，其中步骤1～步骤4用于量化多层网络层权重值以及采用超参数结合了两种不同的加权方法，以适应拓扑结构不同的多层复杂网络。步骤5引入局部密度算法计算节点综合加权局部密度ρ并随着数据集的更新而更新，步骤6则在随机获得种子节点v0后，依据下文第3章中对于选取种子节点不同邻域范围∂内计算社区核心节点获取的社区划分结果进行分析，确定邻域范围并用于计算核心节点集{vi}。步骤7确定并随社区划分更新边界集B和外壳集S，步骤8～步骤13为社区划分过程，步骤14～步骤19为算法划分结果的评估过程,当社区划分结果最优时输出社区C。

3 实验结果和分析

3.1 数据集

该文使用了4个真实世界的多层网络数据集，即AUCS(节点数：61，边数：620，层数：5，2016年)[12]，Airlines(节点数：417，边数：3 588，层数：37，2013年)[13]，Remote Sensing(节点数：642，边数：4 341，层数：5，2016年)[12]和Reality Mining(节点数：88，边数：355，层数：3，2016年)[14-15]。

3.2 评价函数

对于社区划分效果的评价是局部社区检测极其重要的部分，在此处完成所有节点的社区划分后，该文将采用经典的多层社区检测算法GL算法中提出的关于社区划分质量评估的多层模块度函数，用于对文中算法完成划分的社区质量进行评估。

多层模块化质量函数[4]定义如下：

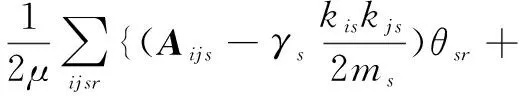
θijCjsr}θ(gis,gjr)

(15)

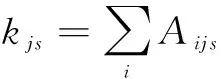
3.3 参数∂的分析

在实验的初始化部分，通过实验选取可变参数n的取值为数据集节点数目的5%，在使用层加权获得节点多层综合加权局部密度之后，随机获得种子节点并依据局部密度确定其所在社区的社区核心节点，在此处设置从种子节点∂阶邻域范围内搜寻核心节点。图1展现了4个数据集在种子节点不同邻域范围内找到的核心节点最终划分结果模块值对比，为使邻域足够大该文分别选取种子节点3阶、5阶、7阶邻域与全局范围内的运行50次实验结果作为对比。

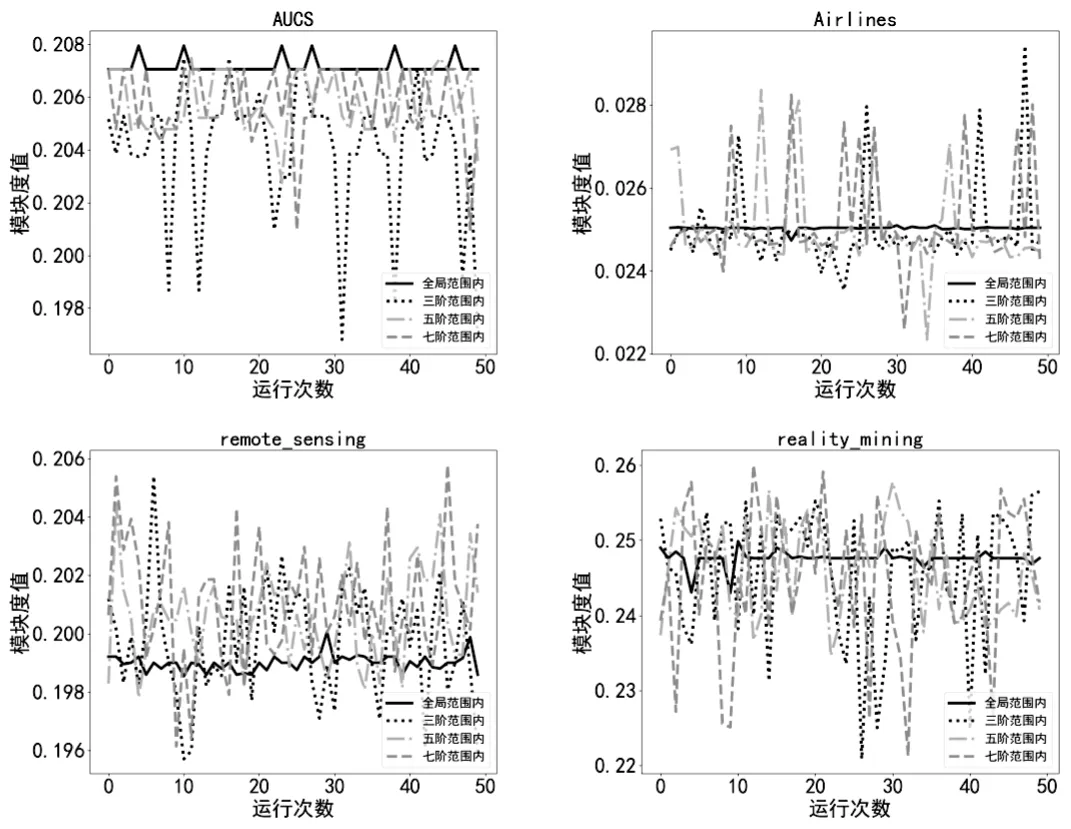
图1 数据集在不同邻域参数∂下运行50次的模块值

由图1所示，选取种子节点∂=3阶以上邻域范围内确定社区核心节点并基于此划分的社区结果接近甚至高于全局社区划分结果，数据集越大效果越明显。实验结果说明了局部社区检测将全局社区检测从一个全局优化问题转化为局部优化问题取得了接近甚至更好的社区划分效果。实验发现当选取邻域超过三阶后，社区划分结果趋于一致，因此在初始化阶段选取种子节点三阶邻域范围内的局部密度最大的两个或者一个节点作为核心节点，并设置核心节点存在于彼此的β=3的邻域范围内，以防止小社区合并的情况出现。

3.4 社区划分评估

关于局部社区检测的评估，对MWLCD算法和ML-LCD算法的性能结果进行了相对较大次数的(平均50次)运行，以减少由于它们的非确定性行为造成的偏差。表1为MWLCD算法与ML-LCD算法进行社区划分结果的平均值对比。

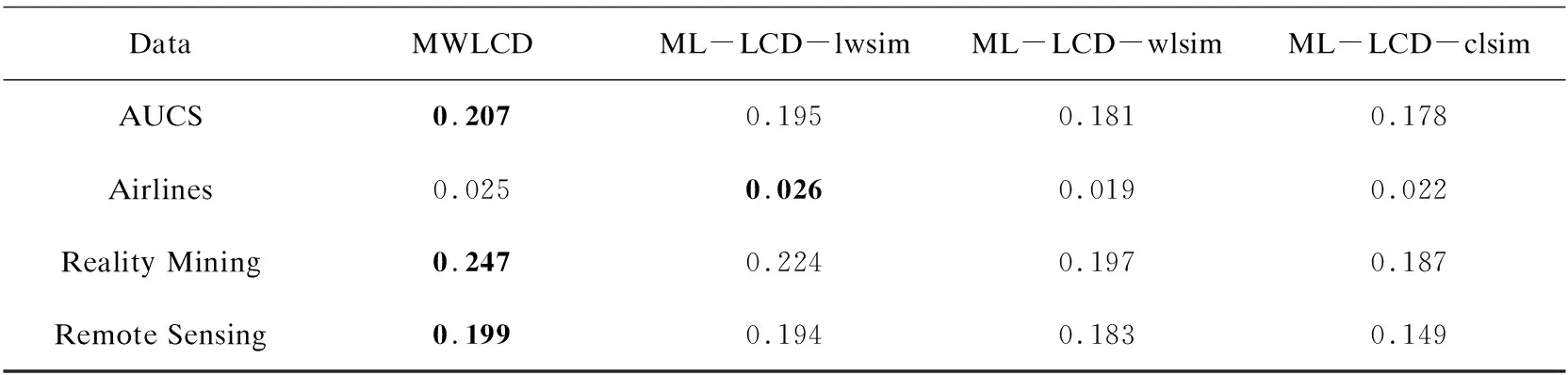
表1 MWLCD与ML-LCD算法运行50次模块度均值

如表1所示，MWLCD算法划分的社区多层模块度值平均值更高，其中黑体值表示最大的模块度均值。

多层局部社区划分往往依赖于种子节点的选取，但该文通过搜索核心节点减少了由于种子节点选取不同导致社区划分结果波动较大的情况，对MWLCD算法和ML-LCD算法的50次运行结果进行了可视化比较。

具体如图2所示。

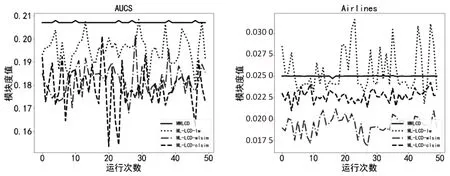
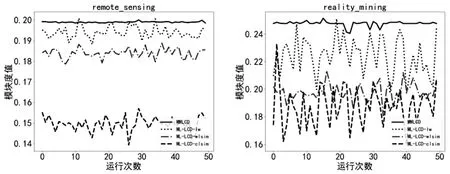
图2 MWLCD与ML-LCD算法运行50次模块度值

图2显示，针对不同的数据集，MWLCD算法除在Airlines数据集中的表现略低于ML-LCD算法，在其他数据集上MWLCD算法均呈现了稳定高效的划分结果。

4 结束语

该文基于网络层加权并引入局部密度算法，构建了一个由随机种子节点确定社区核心节点的多层社交网络局部社区检测算法(MWLCD)。避免了网络规模增大导致的获取全局信息困难的问题，同时在局部社区检测方面获得了更好的社区划分结果。使用4个真实的多层网络数据集对MWLCD算法进行了广泛的实验，MWLCD算法表现出了更高的多层模块性的社区与更强的鲁棒性。未来的研究方向将集中于多层复杂网络中节点在层间相互作用所展现的层相关性等领域。