水库多目标调度优化决策的后悔-灰靶-最大熵模型

邹强　饶光辉　张先平　洪兴骏　李荣波

摘要：针对水库多目标调度方案决策评价问题，引入后悔理论、灰靶理论和最大熵理论并加以综合集成，构建了基于后悔理论-灰靶理论-最大熵理论的水库多目标调度优化决策模型（RT-GT-MET）。首先基于后悔理论来考虑决策者的后悔规避心理和风险偏好态度，构造了基于正负理想点的欣喜-后悔值函数;其次，结合灰靶理论确定正负靶心，利用正负靶心距的空间投影距离建立了综合靶心距函数;然后，引入最大熵理论降低决策过程的不确定性，搭建了集结综合靶心距最小和权重熵值最大的非线性优化模型;最后，结合主客观评价指标权重控制域进行全局优化求解，依据最优综合靶心距实现方案集的决策排序。两个实例应用研究结果验证了所提出模型的合理适用性，表明该模型可以提升水库多目标调度决策的简便性、科学性和造用性，可为水库多目标调度决策提供一种有效的新思路。

关键词：水库调度; 多目标决策; 后悔理论; 灰靶理论; 最大熵理论; 优化求解

中图法分类号： TV697.1

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.02.030

0引 言

水库调度通常承担诸如防洪、供水、生态、发电、航运、应急等多重任务，且多个调度目标之间往往相互影响、相互制约，统筹协调好水库多目标调度、确定满足各方要求的最佳方案是充分发挥水库综合利用效益的关键所在。然而，由于水库多目标调度方案涉及的可行方案非劣性、数据信息的模糊性、决策者认知的主观性、决策者的心理行为态度、评价过程的不确定性等各方面因素，导致决策者难以科学合理地进行多目标、多属性、多层次的复杂决策，水库调度多目标决策理论与方法一直是水库调度领域的重点关注及难点问题。

传统的水库多目标调度决策优选评价方法较多，有灰色关联分析[1]、vague集[2]、TOPSIS[3]、集对分析[4]等，均得到了有益的尝试和发展，推动了水库多目标调度的科学化决策。近年来，该问题仍然受到众多学者的关注，一些新的理论与方法也不断引入应用，例如前景理论[5]、灰靶理论[6]、VIKOR法[7]等，但研究对比发现：前景理论中效用价值函数和前景权重函数的控制参数较多，计算方案前景值的过程也较为复杂;灰靶理论計算过程中需考虑决策者心理因素对决策结果的影响，其适应性研究还有待加强[8];VIKOR模型在权重确定方面忽视了专家主观经验和客观数据分布的复杂性，如何充分有效利用方案集评价信息值得深入研究[9]。特别地，后悔理论与前述的前景理论类似，也是一种考虑决策者心理行为的决策理论，在放弃独立性公理前提下，将后悔和欣喜两种心理感觉纳入决策的偏好关系，相比前景理论具有计算过程简便、控制参数更少等优势，引起了一些学者的热烈关注，已成功应用到城市应急[8]、供应商选择[10]、区域农业抗旱能力[11]等决策研究领域。

为合理反映复杂决策过程中决策者的心理因素，有效处理优化决策涵盖的优化模型建立、模型参数优化、指标权重确定、方案决策排序等难点问题，本文尝试将后悔理论、灰靶理论进行耦合并应用到水库多目标调度决策优选问题中，定义了符合人们思维方式和后悔规避的欣喜-后悔值函数以及综合靶心距函数，以有效描述符合决策者心理行为的最优决策过程;同时，为有效挖掘利用方案集评价的主客观信息，增加对评价指标权重携带信息的利用水平，应用最大熵理论来处理各种不确定性[12]。最终，构建了基于后悔理论-灰靶理论-最大熵理论的水库多目标调度优化决策模型（RT-GT-MET），并结合智能优化方法进行高效求解。通过两个水库多目标调度决策实例，验证了所提模型的合理有效性，提升了水库多目标调度决策的简便性、科学性和适用性，为水库多目标调度决策提供了一种新途径。

2水库多目标调度方案优化决策RT-GT-MET计算流程

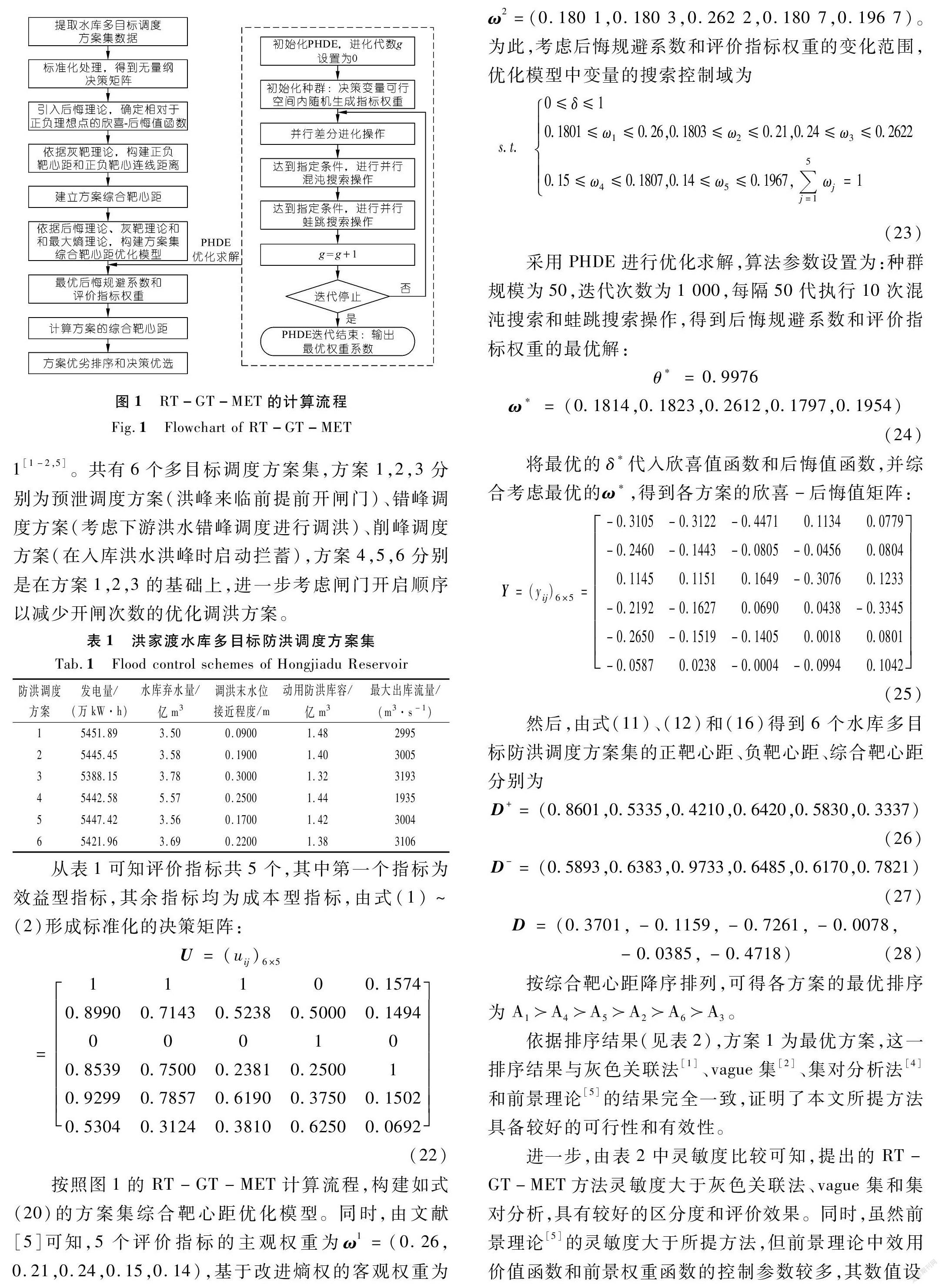
首先，建立特征值决策矩阵及标准化决策矩阵;其次，引入后悔理论构建欣喜-后悔值函数;接着，依据灰靶理论构建各方案的综合靶心距;然后，结合最大熵原理和优化思路构建综合靶心距优化求解模型，并结合PHDE进行后悔规避系数和评价指标权重的决策编码和优化搜索，获得最优的后悔规避系数δ*和价指标权重ω*;最后，依据综合靶心距进行方案排序和决策优选，并比较提出方法与其他方法的决策结果。RT-GT-MET的计算流程如图1所示。

3实例研究

3.1水库多目标防洪调度方案优化决策评价

以乌江流域洪家渡水库的多目标防洪调度决策问题为实例，来分析RT-GT-MET的合理可行性。以洪家渡水库坝址百年一遇的设计洪水过程线为典型来水开展分析，水库多目标防洪调度方案集见表1[1-2，5]。共有6个多目标调度方案集，方案1，2，3分别为预泄调度方案（洪峰来临前提前开闸门）、错峰调度方案（考虑下游洪水错峰调度进行调洪）、削峰调度方案（在入库洪水洪峰时启动拦蓄），方案4，5，6分别是在方案1，2，3的基础上，进一步考虑闸门开启顺序以减少开闸次数的优化调洪方案。

3.2水库群多目标蓄水调度方案优化决策评价

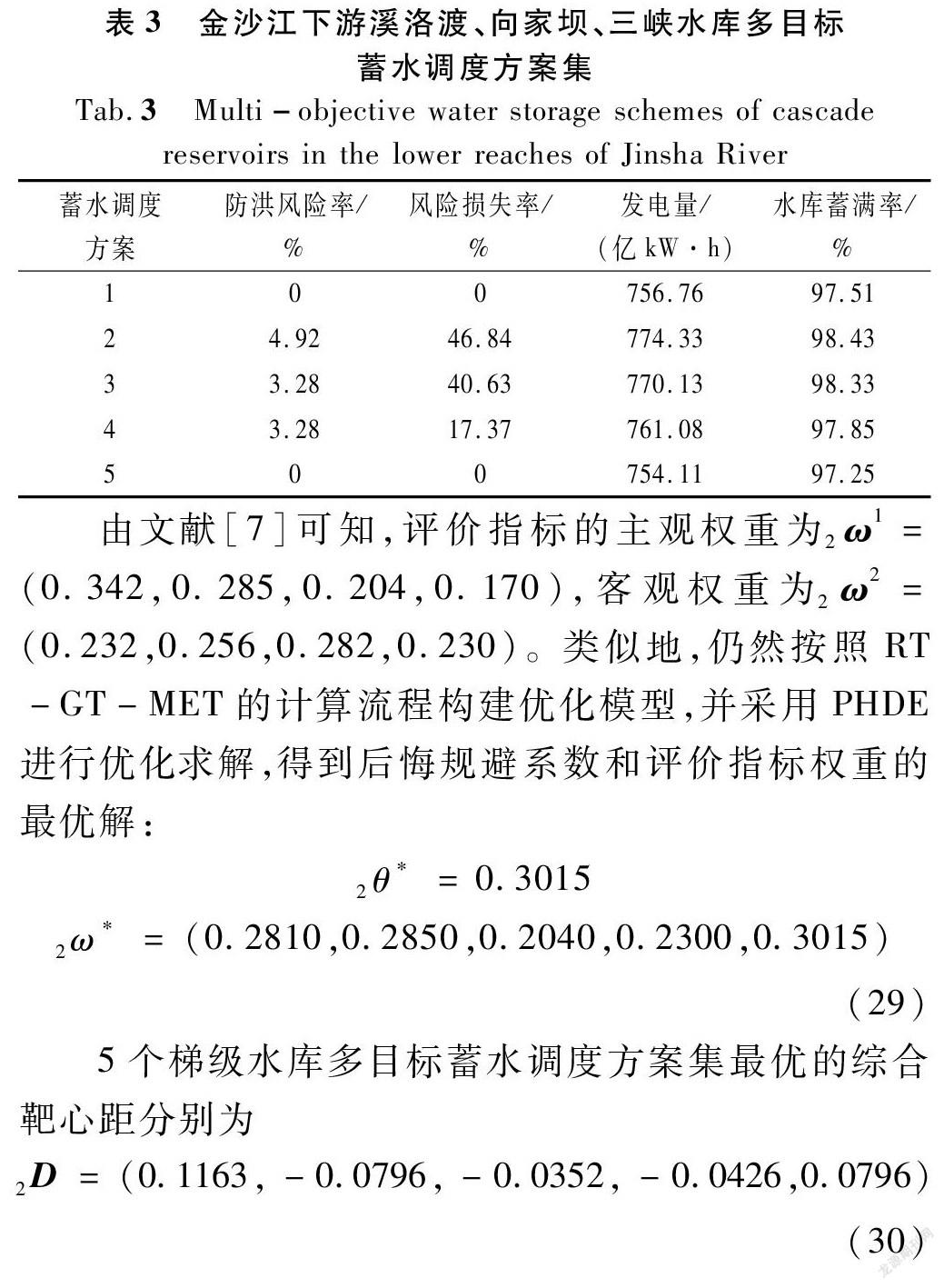
本文还将RT-GT-MET应用到金沙江下游梯级溪洛渡、向家坝、三峡水库多目标蓄水调度方案决策优化问题[7，16]，评价样本集见表3。可见，梯级水库群多目标蓄水调度方案集为5个，评价指标为4个，其中防洪风险率和风险损失率为成本型指标，后两个指标为效益型指标，各指标依据溪洛渡、向家坝、三峡梯级水库1950～2010年共61 a的8月20日至12月31日日均径流实施多目标蓄水调度取长系列平均值得到，梯级水库多目标蓄水调度模型和方案集评价指标计算方法可直接参考文献[16]。限于篇幅，以下直接给出5个方案集及方案决策优选结果。

由文献[7]可知，评价指标的主观权重为2ω1=（0.342，0.285，0.204，0.170），客观权重为2ω2=（0.232，0.256，0.282，0.230）。类似地，仍然按照RT-GT-MET的计算流程构建优化模型，并采用PHDE进行优化求解，得到后悔规避系数和评价指标权重的最优解：

2θ*=0.3015

2ω*=（0.2810，0.2850，0.2040，0.2300，0.3015）（29）

5个梯级水库多目标蓄水调度方案集最优的综合靶心距分别为

2D=（0.1163，-0.0796，-0.0352，-0.0426，0.0796）（30）

按照综合靶心距降序排列，各方案排序为A1A5A3A4A2。依据排序结果，方案1为最优方案，这一最优方案优选结果与MDIP-VIKOR[7]、投影寻踪方法[16]一致，在不降低防洪标准前提下，提高梯级水库综合效益，可为梯级水库群汛末蓄水调度提供科学的决策支持。

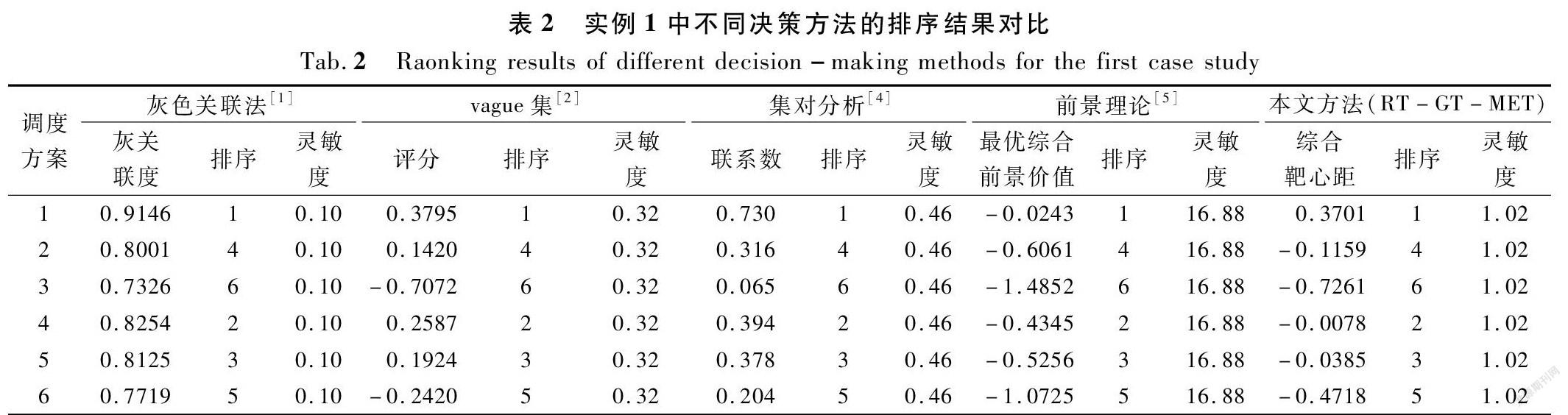
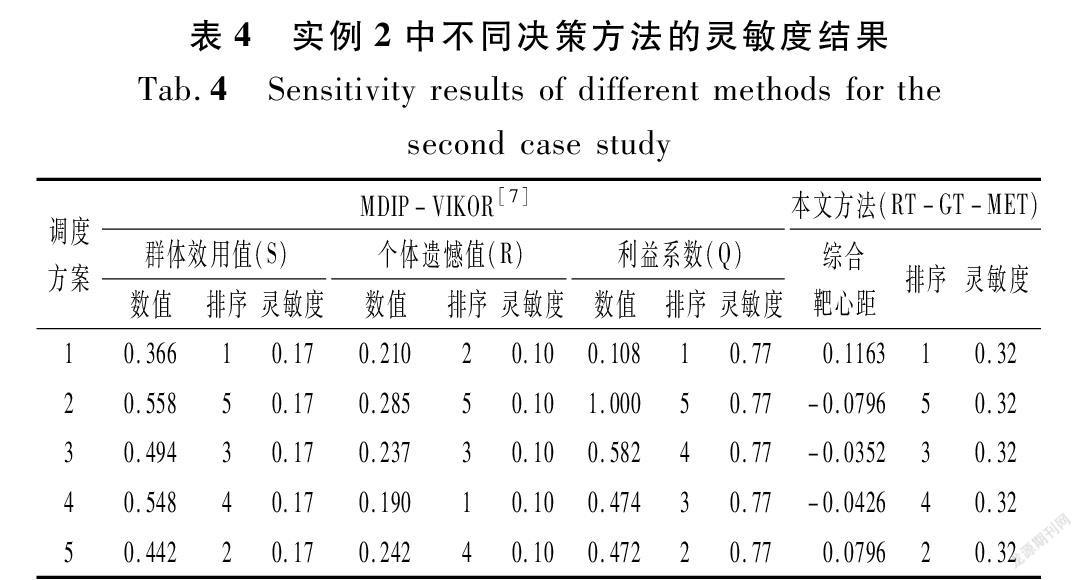
进一步，由表4中灵敏度比较可知，提出的RT-GT-MET方法灵敏度与MDIP-VIKOR灵敏度平均值相当，但后者采用群体效用值、个体遗憾值和利益系数3种决策值进行优选，且排序不尽一样，不易快速进行方案集决策优选，尚需深入进一步有效利用方案集评价信息[9]。而投影寻踪方法尚未考虑评价指标的主观权重，进而导致难以获得指标主客观组合权重，且选取密度窗宽依赖人工经验，尚需进一步融合其他相关理论进行完善以促进其推广应用[17]。

4结 论

在水库多目标调度方案决策优选问题中，方案排序抉择不可避免地需要对理想预期进行估计和憧憬，导致决策结果往往受决策者风险态度影响。为了在灰靶决策过程中充分考虑心理行为因素、避免前景理论中控制参数过多且具有人为主观性的缺陷，本次引入后悔理论这一行为决策理论来解决水库多目标调度方案决策问题，其计算原理简单，控制参数仅有一个，且可有效反映决策者的欣喜和后悔态度;同时，为减少评价过程的不确定性，采用最大熵理论来充分挖掘方案集的评价信息。在以上基础上，提出了基于后悔理论-灰靶理论-最大熵理论的水库多目标调度优化决策模型（RT-GT-MET），构建了综合靶心距最小的非线性优化模型，并结合智能优化算法实现后悔規避系数和指标权重的高效求解，最终以综合靶心距对方案进行优劣排序，为水库多目标防洪、蓄水等各类调度方案决策评价提供了一种新途径。

当然，研究发现，评价指标权重对于排序结果具有较大影响，如何有效挖掘指标权重信息、分析指标权重的模糊不确定性对决策影响，是下一步需要重点攻关的研究内容。

参考文献：

[1]马志鹏，陈守伦，李晓英.多目标水库洪水调度方案的灰色优选[J].三峡大学学报（自然科学版），2007，29（4）：289-291.

[2]李英海，周建中.基于改进熵权和Vague集的多目标防洪调度决策方法[J].水电能源科学，2010，28（6）：32-35.

[3]武新宇，范祥莉，程春田，等.基于灰色关联度与理想点法的梯级水电站多目标优化调度方法[J].水利学报，2012，43（4）：422-428.

[4]卢有麟，陈金松，祁进，等.基于改进熵权和集对分析的水库多目标防洪调度决策方法研究[J].水电能源科学，2015，33（1）：43-46.

[5]邹强，张利升，李文俊.基于累积前景理论和最大熵理论的水库多目标防洪调度决策方法[J].水电能源科学，2018，36（1）：57-60，56.

[6]李安强，李荣波，何小聪.基于灰靶理论的水库调度方案决策模型及其应用[J].人民长江，2018，49（13）：90-94.

[7]李荣波，李安强，游中琼，等.基于MDIP-VIKOR的水库多目标调度方案评价模型[J].人民长江，2019，50（5）：191-195.

[8]郭三党，刘思峰，方志耕.基于后悔理论的多目标灰靶决策方法[J].控制与决策，2015，30（9）：1635-1640.

[9]郑玉婷，王丽萍，谢宇韬，等.改进的VIKOR决策模型在大隆水库汛期水位动态控制中的应用[J].水电能源科学，2020，38（6）：38-41.

[10]郭三党，李晔，陈晓燕.基于后悔理论的多时点风险灰靶决策方法[J].数学的实践与认识，2018，48（21）：1-8.

[11]罗党，王付冰.区域农业抗旱能力风险评估中的混合灰靶决策方法[J].华北水利水电大学学报（自然科学版），2018，39（6）：66-71.

[12]邹强，周建中，周超，等.基于最大熵原理和属性区间识别理论的洪水灾害风险分析[J].水科学进展，2012，23（3）：323-334.

[13]BELL D E.Regret in decision making under uncertain[J].Operations Research，1982，30（5）：961-981.

[14]LOOMES G，SUGDEN R.Regret theory：an alternative theory of rational choice under uncertainty[J].Economic Journal，1982，92（368）：805-824.

[15]邹强，鲁军，周超，等.基于并行混合差分进化算法的梯级水库群优化调度研究[J].水力发电学报，2017，36（6）：57-68.

[16]周研来，郭生练，陈进.溪洛渡-向家坝-三峡梯级水库联合蓄水方案与多目标决策研究[J].水利学报，2015，46（10）：1135-1144.

[17]廖力，邹强，何耀耀，等.基于模糊投影寻踪聚类的洪灾评估模型[J].系统工程理论与实践，2015，35（9）：2422-2432.

（编辑：刘 媛）