卡洛特水电站埋藏式压力钢管联合受力研究

汪碧飞　李月伟　孔剑　胡剑杰

摘要：考虑钢管与围岩联合承载，采用有限元对钢管、回填混凝土与围岩组成的联合承载体进行了非线性的计算分析，将有限元计算结果与规范计算结果进行了对比，比较了内水压力、围岩与钢管缝隙等因素对钢管受力特性及围岩分担率的影响。研究表明：不同的内水压力下，围岩分担率不同，一般随内水压力的增加而减小。缝隙影响围岩的分担率，缝隙越小，围岩分担的内水压力就越大;当缝隙超过一定值时，钢管接近明管的受力状态。回填混凝土采用弹塑性断裂本构模型的实体单元模拟能较好地反映材料的力学性能，宜采用该方法对埋藏式压力钢管进行受力分析与工程设计。

关键词：埋藏式压力钢管; 联合承载; 三维有限元模型; 围岩分担率

中图法分类号： TV732.41

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.02.023

0引 言

埋藏式钢管在水利水电工程、石油化工等领域的应用越来越普遍。已有许多学者对埋藏式岔管的结构特性、岔管与围岩的联合承载机理进行了深入研究[1-5]。丁柳旭等[3]通过建立围岩、回填混凝土及钢管的三维有限元模型，得到了岔管的应力与岔管关键点的围岩分担率，但没有考虑岔管外回填混凝土的塑性性质。田静等[6]将岔管周围的回填混凝土与围岩简化为施加在管壁外侧的弹簧，并对岔管进行有限元分析，获得了岔管的一些受力特性。燕乔等[7]采用D-P模型，分析了岔管、回填混凝土及围岩的联合承载特点，其结论是岔管周围的绝大部分混凝土都已屈服，表明混凝土超过了抗拉强度出现开裂，混凝土一旦开裂后，承载力不再增加，内部应力会进行调整，因此钢衬应力可能大于计算值，但没有对混凝土的开裂特性进行分析。陈莉静等[8]在线弹性条件下，将钢管与混凝土之间的缝隙定義为不密实接触层，根据变形协调条件，推导了钢管、接触层、混凝土层及围岩等各层的变形解析解，从而计算出了围岩分担率，其研究模型假定条件较多，解析过程推导复杂。汪碧飞等[9]分析了混凝土采用不同本构模型、围岩弹性模量等因素对钢管受力特性及围岩分担率的影响，研究表明回填混凝土采用弹塑性断裂本构模型能较好地模拟埋藏式压力钢管的受力。

本文建立了钢管、回填混凝土及围岩的有限元模型，其中，回填混凝土与围岩采用两种不同的单元模拟。通过3种方法对埋藏式钢管进行计算分析：

① 按SL/T 281-2020《水利水电工程压力钢管设计规范》[10]推荐公式计算;

② 利用ANSYS有限元分析，回填混凝土与围岩采用实体单元模拟，并考虑回填混凝土的弹塑性断裂特性;

③ 利用ANSYS有限元分析，回填混凝土与围岩简化为弹簧单元模拟。

并比较了3种分析方法下内水压力、钢管与围岩之间缝隙等因素对钢管受力特性及围岩分担率的影响，可为埋藏式钢管或埋藏式钢岔管的设计提供依据。

1工程概况与计算方法

1.1工程概况

卡洛特水电站采用岸边引水式地面厂房，布置在右岸，引水隧洞位于河湾地块中部吉拉姆河 Ⅱ 级阶地，地形较完整，地面高程485～460 m，两侧高，中间低，上游侧斜坡地形坡度12°～22°，下游侧地形总体平坦，坡度5°左右，局部达15°。覆盖层主要为残坡积（Qedl）黏土夹碎石，（Q2-3all+pl）砂壤土、砂砾卵石层，厚约1～13 m，下伏基岩由N1dh组及N1na组弱风化～微风化泥质粉砂岩与粉砂质泥岩互层及砂岩组成，岩层走向N5°E～N10°E，倾向SEE，倾角9°～10°，完整性总体较好，砂岩一般为较软岩，泥质粉砂岩与粉砂质泥岩一般为软岩，泥质粉砂岩、粉砂质泥岩强度低，具失水干裂、遇水崩解的特性。岩体以Ⅲ、Ⅳ类为主，局部V类。水库正常蓄水位461.00 m，引水隧洞钢管由上弯段、斜直段、下弯段、锥管段和下平段组成，钢管直径9.6 m，在下弯段后经锥管段直径缩减为7.9m，钢管埋设较深，可按埋藏式压力钢管进行设计，选取直径9.6 m的钢管计算分析，最大设计水头116.5m，钢管材质Q345R。

1.2规范计算

根据SL/T 281-2020《水利水电工程压力钢管设计规范》[10]，当缝隙Δ<σφr/E′时，钢管环向应力按式（1）计算，管壁厚度按式（2）计算;当缝隙Δ≥σφr/E′时，不考虑围岩分担率，按锅炉公式计算环向应力。

σθ=pr+1000K0Δt+1000K0r/E′（1）

t=pr[σ]φ+1000K0Δ[σ]φ-rE′（2）

式中：K0为围岩单位抗力系数;E′=E/（1-v2），E为钢材弹性模量;p为内水压力;φ为焊缝系数，r为钢管半径。

1.3实体单元

利用ANSYS有限元程序计算，假定开挖后地应力全部释放，忽略地应力对钢管的影响。围岩、回填混凝土与钢管为各向同性材料[11]，围岩与钢管采用线弹性模型，回填混凝土采用弹塑性断裂模型[9]。采用SOLID65单元模拟[12]回填混凝土的开裂、压碎等力学现象，可使用的本构关系有等强硬化模型（Multilinear isotropic hardening）、随动硬化模型（Multilinear kinematic hardening）和Drucker-Prager（D-P）模型，本文使用等强硬化模型定义混凝土的硬化法则。SOLID65单元采用William-Warnke五参数模型的破坏准则[13-14]，TB（concr）参数用来定义混凝土开裂与压碎，TB（miso）参数用来定义混凝土的应力应变关系。取混凝土的单轴抗拉强度与单轴抗压强度分别为3 MPa与30 MPa，裂缝张开传递系数与闭合传递系数分别为0.5与0.95。

围岩与回填混凝土有限元网格共节点，围岩采用实体单元SOLID185模拟，钢管采用壳单元SHELL181模拟，钢管与回填混凝土之间设置面-面接触单元，采用库仑摩擦模型模拟回填混凝土与钢管之间的相互作用，接触面间的相互作用包括法向作用与切向作用，当缝隙闭合时传递法向压力，缝隙张开时不传力，钢管与回填混凝土的接触面可以相对滑动，钢管与回填混凝土的摩擦系数为0.4，钢管与回填混凝土之间摩擦力最大值不超过0.2 MPa[15]。材料力学参数见表1。有限元模型外轮廓为六面体，沿钢管轴向长90 m，钢管中心线至顶面与侧面的垂直距离均为30 m，固定围岩底面，对称约束六面体剩下的5个面。埋藏式钢管有限元模型见图1。

1.4弹簧单元

将回填混凝土与围岩简化为整体，假定回填混凝土与围岩对钢管为法向弹性约束作用，法向弹性约束作用类似为弹性连杆，用ANSYS软件中点对点接触单元CONTAC178模拟钢管与围岩的联合承载机理，回填混凝土与围岩简化为具有一定刚度的弹簧单元CONTAC178，钢管采用壳单元SHELL181模拟，弹簧单元的刚度根据围岩的力学性能与钢管有限元网格大小确定。点对点接触弹簧单元由I、J两个节点组成，I节点位于管壳表面，J节点位于管壳外法线上一定距离处，该距离表示钢管与围岩之间的缝隙值（见图2）。

围岩弹性抗力系数和弹性模量之间的换算关系根据喀列尔金公式计算：

K=E（1+v）R0（3）

式中：K为围岩弹性抗力系数，E为围岩弹性模量，v为围岩的泊松比，R0为洞室半径。

围岩单位弹性抗力系数是指洞室半径为100 cm时的抗力系数值：

K0=K×R0100=E（1+v）×100（4）

弹簧的压缩刚度与拉伸刚度取值如下：

（1） 当弹簧单元处于压缩状态时，弹簧刚度系数为：

k=K0×An（5）

式中：A为管壁面积，n为有限元模型管壁的节点个数。

（2） 当弹簧单元处于拉伸状态时，弹簧刚度系数为零。

2计算结果对比

分析了3种计算方法下内水压力、钢管与回填混凝土之间的缝隙对钢管受力特性及围岩分担率的影响。围岩分担率定义为：计算明钢管、埋藏式钢管在内水压力作用下钢管的环向膜应力的均值，埋藏式钢管应力与明钢管应力的差值除以明钢管应力即为围岩分担率。

2.1内水压力的影响

埋藏式钢管的允许应力σ=0.67σs=0.67×325=217.8 MPa;取围岩弹性模量1.25 GPa，按弹性理论计算，围岩单位抗力系数为10 MPa/cm;σφr/E′=4.39 mm，規范[10]建议的缝隙值3.0×10-4r～5.5×10-4r，取钢管与回填混凝土之间的缝隙Δ=5.5×10-4r=2.64 mm，满足Δ<σφr/E′，可按公式（1）与公式（2）计算钢管环向应力与钢管壁厚。

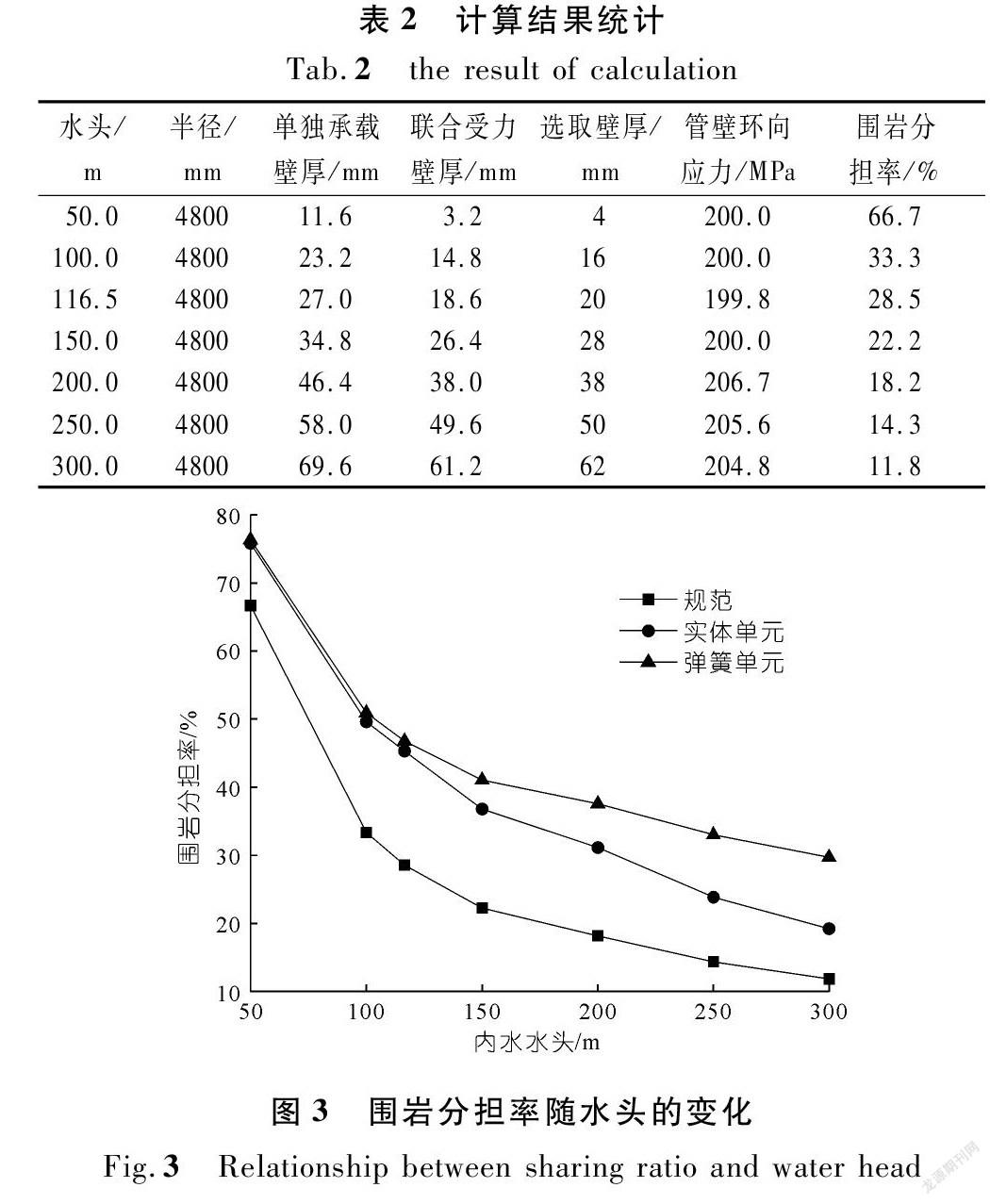
规范计算的结果见表2，根据构造要求，钢管最小壁厚为16 mm，为方便进行比较分析，水头50 m时钢管壁厚按实际计算值取4 mm，在不同水头下，有限元模型中管壁的厚度与表2中的“选取壁厚”一致，水头与围岩分担率的曲线关系见图3。由计算结果得知：① 规范计算的围岩分担率最低，围岩采用弹簧单元计算的围岩分担率最高，围岩采用实体单元计算的围岩分担率介于两者之间。② 围岩分担率一般随内水压力的增加而减小，因为钢材一旦选定，其允许应力及对应的钢管径向变形就一定，相应的围岩抗力（或反力）也就一定，无论内水压力增加多少，围岩承担的内水压力绝对值都是一样的，使得承载比随内压不断降低。③ 内压低于50 m水头时，3种方法计算的围岩分担率接近;100～200 m水头时，围岩采用实体单元和弹簧单元计算的围岩分担率接近，与规范计算结果相差较大，内压越大，弹簧单元计算的围岩分担率与实体单元的结果相差越大;水头300 m时，规范、实体单元及弹簧单元计算的围岩分担率分别为11.8%，19.2%及29.7%。④ 规范方法与围岩简化为弹簧单元的有限元法计算时假设的边界条件较多，计算结果存在一定的偏差，而回填混凝土采用弹塑性断裂本构模型的实体单元模拟能较好地反映材料的力学性能，特别是当内压较高，回填混凝土进入塑性、出现裂纹时，该方法适应性更好。

2.2缝隙的影响

由于钢管与回填混凝土冷缩、施工等原因，钢管与回填混凝土之间存在初始缝隙，缝隙影响内水压力的分配。内水压力作用下，当钢管的变形充满缝隙时，钢管与回填混凝土接触，回填混凝土与围岩开始对钢管产生径向约束，共同承受内水压力。内压116.5 m水头，壁厚20 mm，取不同的缝隙值计算，分析缝隙值变化对钢管应力与变形的影响，缝隙分别取0，3×10-4r，5.5×10-4r，8×10-4r，12×10-4r，16×10-4r。

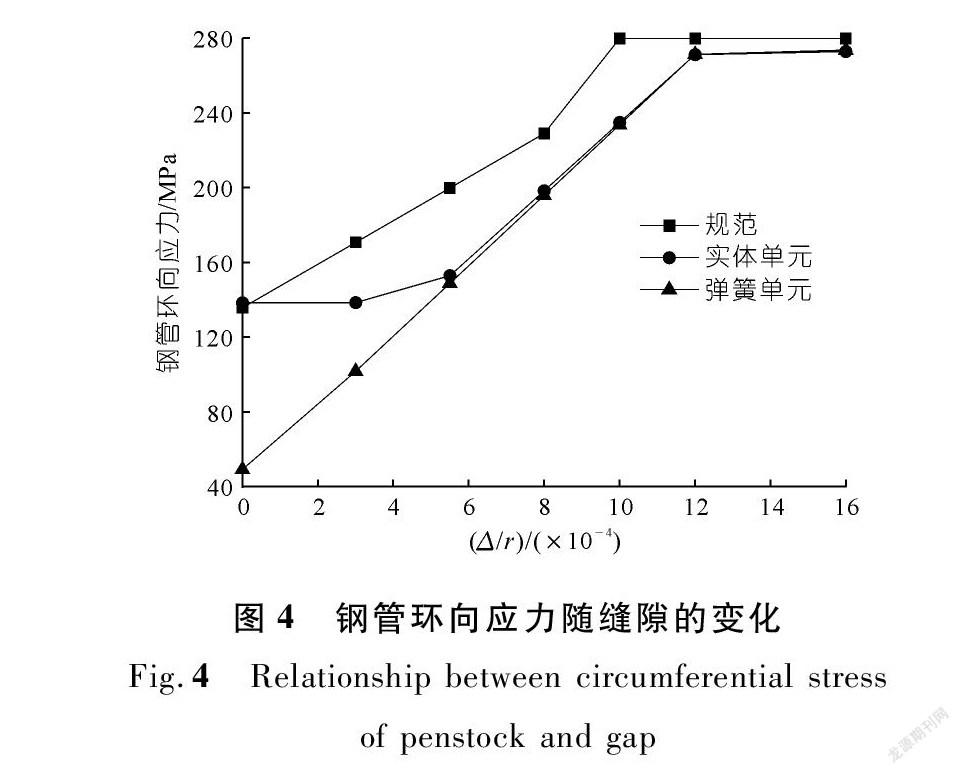
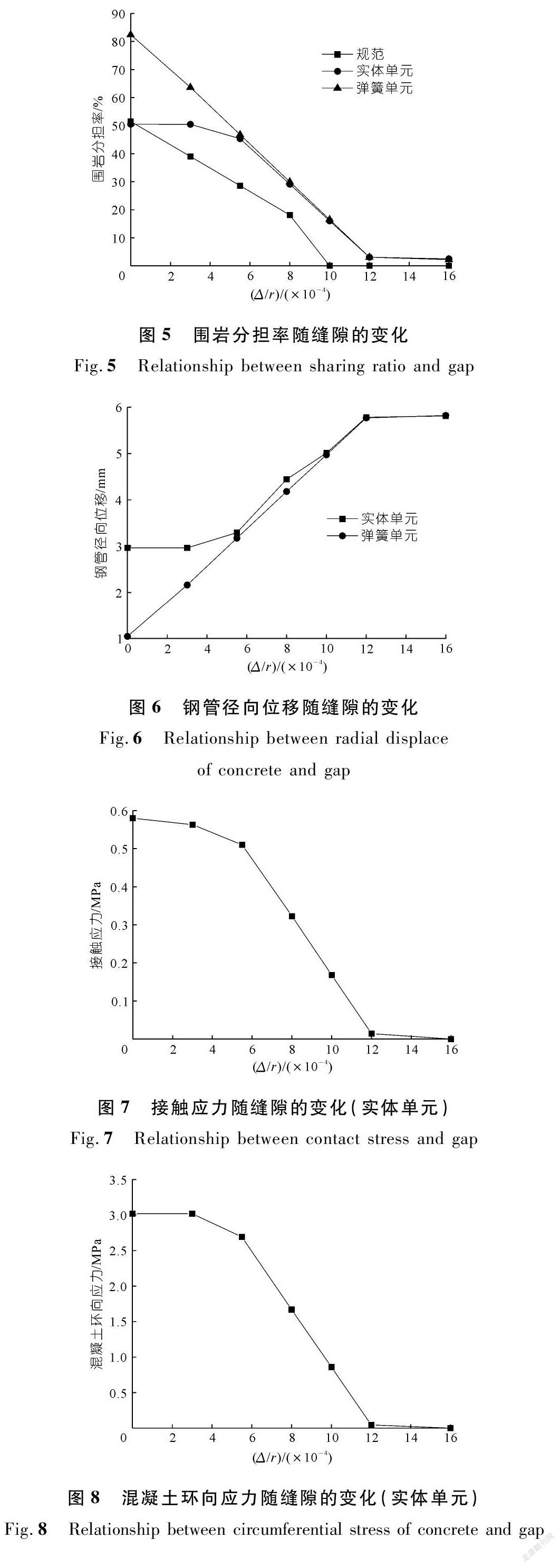
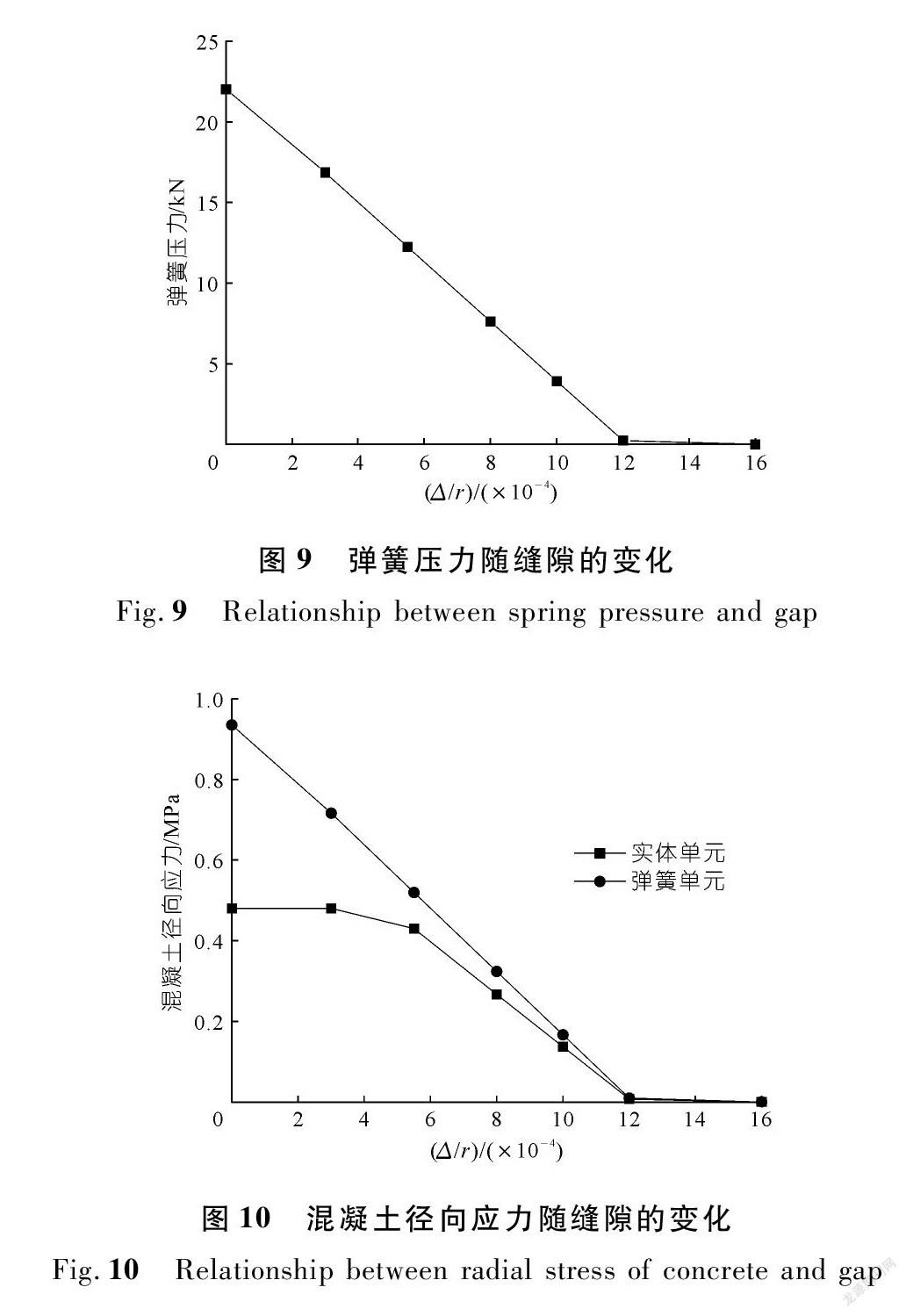
钢管环向应力、围岩分担率、钢管径向位移、接触应力（实体单元）、混凝土环向应力（实体单元）、弹簧压力、混凝土径向应力分别见图4～10。由计算结果得知：① 规范计算的围岩分担率最低，当缝隙超过5.5×10-4r后，围岩采用实体单元与弹簧单元计算围岩分担率非常接近。这是由于缝隙值较大时，回填混凝土收到的水压力较小，回填混凝土还没有进入塑性状态，因此实体单元与弹簧单元结果较为接近。② 钢管的环向应力与径向位移随缝隙的增加而增加。围岩分担率、接触应力、混凝土环向应力、弹簧压力及混凝土径向应力随缝隙的增加而减小。③ 缝隙在0～8×10-4r范围时，围岩分担率较高;当缝隙超过8×10-4r后，围岩分担率下降明显;当缝隙超过12×10-4r后，钢管受力接近明管受力状态。因此，应加强回填混凝土的浇筑质量，尽量减少初始缝隙，充分发挥围岩的对钢管的径向约束，使初始缝隙在8×10-4r以内。④ 围岩采用弹簧单元计算得到单根弹簧的压力，通过单根弹簧所对应的管壁面积换算出管壁受到的围岩等效压应力，即混凝土的径向压应力。图10比较了实体单元与弹簧单元下回填混凝土的径向压应力，相比实体单元，采用弹簧单元时回填混凝土的径向压应力更大，相应的围岩分担率更高。

3结 论

通过3种方法对埋藏式压力钢管的计算分析，得到如下结论：

（1） 不同的内水压力下，围岩分担率不同，一般随内水压力的增加而减小。

（2） 缝隙影响围岩的分担率，缝隙越小，钢管受到围岩的约束越大，围岩分担的内水压力就越大。当缝隙超过一定值时，钢管接近明管的受力状态，应加强混凝土浇筑质量，进行灌浆以减小缝隙。

（3） 规范方法简单明了，应用方便，但由于该方法基于弹性理论推导，假定的计算边界条件较多，计算结果偏于安全。回填混凝土与围岩采用弹簧单元模拟，弹簧刚度由围岩弹性模量、回填混凝土的弹性模量及有限元网格大小确定，是一种材料线弹性假设，无法全面反映材料的力学性能，适应于内压较低的埋藏式钢管，当内压较高时，计算结果与规范方法相差较大，该方法的优点是建立模型、划分单元方便，计算易收敛。回填混凝土与围岩采用实体单元、回填混凝土采用弹塑性断裂本构模型的有限元法能较好的反映材料的力学性能，计算结果较为合理，特别是当内压较高，回填混凝土进入塑性、出现裂纹时，该方法适应性更好。但对于体型复杂的埋藏式岔管建模工作量大，计算不易收敛，对有限元網格要求较高，需精细划分网格。

参考文献：

[1]伍鹤皋，石长征，苏凯.埋藏式月牙肋钢岔结构特性研究[J].水利学报，2008，39（4）：460-465.

[2]李旻，伍鹤皋.埋藏式钢岔管与围岩联合承载有限元分析[J].武汉大学学报（工学版），2004，37（1）：23-26.

[3]丁柳旭，伍鹤皋，龚玉峰.地下埋藏式钢岔管承载机理研究[J].水利学报，2003，34（4）：119-123.

[4]汪碧飞，李勇泉，陈美娟，等.埋藏式月牙肋岔管内压分担比研究[J].长江科学院院报，2021，38（6）：123-127.

[5]符志远.压力钢管联合受力多层环模型及算法[J].人民长江，1995，26（5）：1-9.

[6]田静，楚万强，许性永，等.埋藏式月牙肋钢岔管结构三维有限元分析[J].水电能源科学，2011，29（5）：86-88.

[7]燕乔.地下埋藏式钢岔管结构三维有限元分析[J].水力发电，2003，29（6）：29-32.

[8]陈莉静，李宁，韩信.考虑不密实接触地下埋管联合受力分析[J].西北农林科技大学学报（自然科学版），2005，33（6）：113-116.

[9]汪碧飞，李勇泉，陈美娟，等.埋藏式钢管与围岩联合承载研究[J].水电能源科学，2021，39（1）：115-118.

[10]中华人民共和国水利部.水利水电工程压力钢管设计规范：SL/T 281-2020[S].北京：中国水利水电出版社，2020.

[11]陈明祥.弹塑性力学[M].北京：科学出版社，2007.

[12]陆新征，江见鲸.ANSYS Solid65 单元分析混凝土组合构件复杂应力[J].建筑结构，2003，33（6）：22-24.

[13]张建华，苏凯，伍鹤皋.钢筋混凝土岔管结构分析与配筋优化[J].人民长江，2009，40（24）：12-15.

[14]马文亮，李晓芬，陈卫星.龙开口电站钢衬钢筋混凝土坝后背管非线性分析[J].人民长江，2012，43（15）：7-10.

[15]方诗圣，丁仕洪.钢围堰封底混凝土与桩基钢护筒间的粘结力研究[J].合肥工业大学学报（自然科学版），2009，32（2）：241-244.

（编辑：黄文晋）