南海东部地区古近系测压资料流度校正与渗透率升尺度转换模型

石 磊，冯 进，刘道理，管 耀，李晓东，孙建孟，潘卫国

（1.中海石油（中国）有限公司深圳分公司南海东部石油研究院，广东深圳 518000；2.中国石油大学（华东）地球科学与技术学院，山东青岛 266580）

电缆地层测试技术在海上油气田应用广泛，在替代钻杆地层测试（DST）节省成本等方面正发挥着越来越重要的作用［1-2］。与传统试油分析和常规岩心分析相比，电缆地层测试优势更为明显，不仅能够准确得到任意深度地层的压力资料进而表征地层流体渗流特征，且作业时间短，更为经济。但是，由于电缆地层测试的压力预测试抽吸体积小、波及范围小，测量结果只能反映地层冲洗带泥浆滤液的渗流特性，所以测压流度不可避免地受泥浆侵入所造成的储层污染的影响。马建国等介绍了电缆地层测试确定储层参数的方法，包括污染系数等储层损害性参数的确定方法［3］；蔡军等给出储层污染综合指数以及由流度和综合指标交会图给出的储层污染程度判别标准图版［4］。但这些方法未从测压质量入手进行系统评估，具有一定局限性。鹿克峰等均提出利用岩心相渗实验建立相关关系，将低渗透气藏电缆地层测试流度转换为气相渗透率的方法［5-6］；高永德等利用球形流流度建立视径向流流度计算方法，然后通过区域相渗资料、流体黏度将视径向流流度转换为有效渗透率［7］。以上方法转换后的渗透率仍为离散的单点渗透率，未充分利用测井获得的连续渗透率曲线进行升尺度转换研究，难以实现与DST渗透率的精确对比。

为此，以南海东部地区古近系低渗透储层为主要研究对象，通过对测压资料质量定量评价、流度归一化、储层污染校正、渗透率升尺度转换等处理，显著改善了电缆地层测试渗透率与DST 渗透率评价精度。

1 测压资料质量定量评价及流度计算

1.1 古近系测压资料质量评价方法的改进

测压资料质量一般包含有效点、致密点、干点、超压和坐封失败点等多种类型［8］。由于不同仪器对测压资料质量评价标准不同，导致现场对储层物性认识存在歧义。为了统一认识，重新对测压资料质量进行定量评价，通过敏感性分析，最终采用压力恢复三参数建立综合评价标准：①压力稳定性参数，即压力恢复最后60 s 压力数据的线性回归线斜率。②压力测量稳定性参数，即压力恢复最后60 s压力数据在线性回归线附近的离散度。③温度稳定性参数，即压力恢复最后60 s 温度数据的线性回归线斜率［9］。引入基于上述参数的测压质量评价分数，其表达式为：

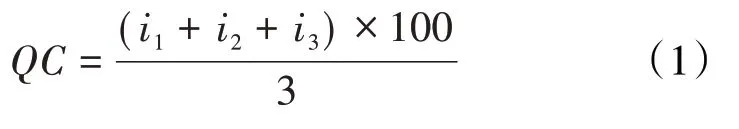
如果压力稳定性参数小于阈值，则i1=1，反之，i1=0；如果压力测量稳定性参数小于阈值，则i2=1，反之，i2=0；如果温度稳定性参数小于阈值，则i3=1，反之，i3=0。电缆地层测试测压资料质量评价分数越高，代表测压资料质量越好，流度测量结果更可靠。剔除低质量评价分数（QC≤33）流度资料点后，能有效提升流度与岩心渗透率的相关关系。

考虑到研究区不同储层类型物性差异较大，采用同一质量评价参数阈值会造成测压资料质量的误判。统计研究区古近系储层物性数据，岩心渗透率为1 mD 左右，资料点流度主要为1 mD/（mPa·s）。选取研究区163 个有效测压点数据，按储层类型分别确定这3个质量评价参数的阈值，结果参见表1。

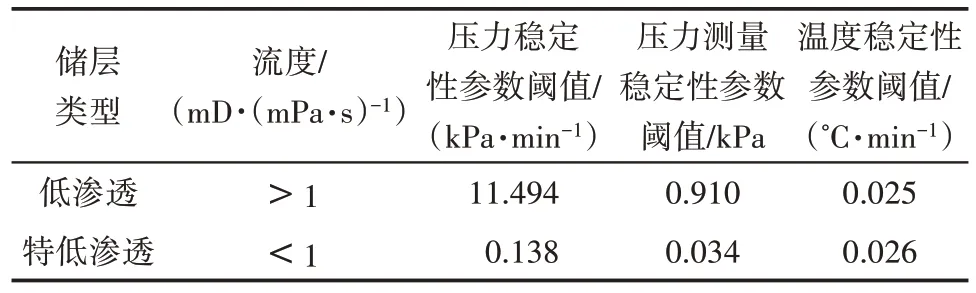
表1 测压数据质量评价参数阈值Table1 Thresholds of quality evaluation parameters of pressure data

1.2 测压资料流度归一化处理

研究靶区电缆地层测试仪器主要有斯伦贝谢的MDT 和贝克休斯的RCI 等。不同仪器流度计算方法不同，造成测压流度存在较大差异，对渗透率计算造成显著影响［10］。流度计算方法主要包括2种：①压降稳态法是基于球形渗流方程稳定解的方法［11］。②面积积分法是一种改进的压降稳态法［12］。

西江-24 井主要目的层为古近系文昌组砂岩，埋藏较深，为4 043.5～4 481.8 m，岩性主要为细砂岩及中砂岩，孔隙度为10%～15%，渗透率为0.5～47.3 mD，相近孔隙度对应的渗透率差异较大，储层非均质性较强，现场物性识别主要依赖地层压力测试［13-14］。该井在目的层分别进行了RCI测压作业和MDT测压作业，RCI测压点流度由压降稳态法得出，MDT 测压点流度由面积积分法得出。从图1a 中可以看出，RCI 流度和MDT 流度在相同埋深下分布不一致，且RCI 流度普遍比MDT 流度大一个数量级。在实际测试过程中，低渗透储层的流动压力不稳定，压降稳态法计算的流度结果存在不确定性，而面积积分法可以通过数学方法对未出现稳态流的压力进行校正，计算得到更准确的流度［15］。

基于上述认识，统一采用面积积分法处理西江-24 井的MDT 和RCI 的测压资料，从图1b 可以看出，RCI 流度和MDT 流度在相同埋深下分布较一致，消除了不同仪器流度计算方法对流度结果的影响。

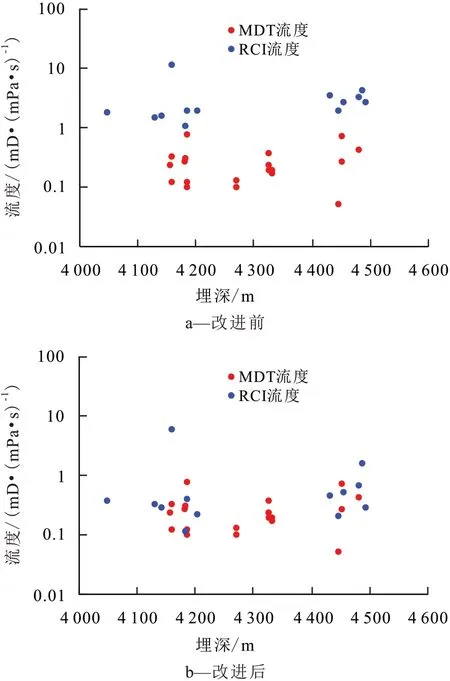
图1 西江-24井流度计算方法改进前后流度分布对比Fig.1 Comparison of mobility distribution before and after improvement of mobility calculation method in Well Xijiang-24

2 储层污染识别

2.1 岩心条件下储层污染评价

测量岩心渗透率前，需对岩心样品进行适当的洗油洗盐等操作，实验测量的岩心渗透率就基本等于不受地层污染影响的绝对渗透率，而流度反映的是冲洗带的水相渗透率，两者之间存在相态差异［16］。相比绝对渗透率，水相渗透率不仅反映了岩心本身的属性，而且反映了水在岩石中的分布以及他们之间的相互作用［17］。通过区域资料确定储层泥浆滤液的黏度、水相渗透率与绝对渗透率的转换关系后，将流度转换为绝对渗透率，即测压渗透率，从而消除流度与岩心渗透率的相态差异。

统计研究区测压点对应的岩心实验数据，建立测压渗透率与岩心渗透率的关系（图2），同一深度测压渗透率和对应的岩心渗透率相差数倍甚至百倍，原因在于储层污染［18-20］。受泥浆滤液污染的影响，流度测量值变小，从而计算的测压渗透率会明显偏小，导致测压渗透率与对应的岩心渗透率存在较大差异。为此，结合岩心、测压与测试资料开展近井带储层污染评价研究，建立流度校正模型，提高测压资料评价储层精度。

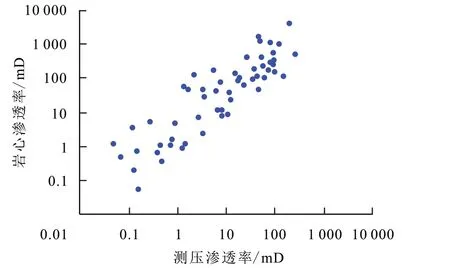
图2 测压渗透率与岩心渗透率的关系Fig.2 Relationship between pressure measurement permeability and core permeability

储层没有受到污染时，岩心渗透率与对应的测压渗透率相等，岩心渗透率与测压渗透率比值即为1；当岩心渗透率与测压渗透率比越大，表明流度测量值受污染影响较大，即岩心渗透率与测压渗透率比越大表明储层污染越严重。据此可以定量评价储层受污染的程度，定义岩心渗透率与测压渗透率比为表征储层污染的污染指数，其表达式为：

依据污染指数计算结果，对储层污染程度进行定量划分：当污染指数小于2 时，定义为轻度污染；当污染指数为2～7时，定义为中度污染；当污染指数大于7 时，定义为重度污染。统计出不同污染程度的岩心渗透率与测压渗透率的关系，建立测压渗透率校正到岩心渗透率的污染校正公式（图3）。重度污染、中度污染、轻度污染的校正计算式分别为：

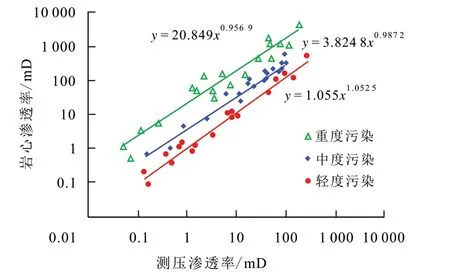
图3 储层污染划分及校正Fig.3 Reservoir pollution partition and correction

2.2 无岩心条件下储层污染识别

针对在无岩心条件下，测压流度测量值受储层污染影响而校正难的问题，采用贝叶斯判别法识别储层污染程度。由于泥浆污染会导致近井带地层压力变化，压力预测试反映近井带地层，所以测压时的压力变化会携带泥浆污染信息，可用泥浆压力、地层压力、预测试体积等测压参数来评价储层污染程度［21-22］。

贝叶斯判别法认为空间中有G个互相独立的总体，均服从多元正态分布，且协方差相同。利用已经确定的变量数据，考虑先验概率，建立每个总体的判别函数，计算待判别样本属于每个总体的条件概率，条件概率最大的总体即为该样本所属的类别［23］。基于储层污染程度，通过贝叶斯判别法，由泥浆压力、地层压力、预测试体积等测压参数建立了储层污染程度的贝叶斯判别函数。基于岩心条件下测压点的储层污染划分数据，储层污染判别结果（表2）显示，贝叶斯判别函数对84.8%的分组验证分类数据进行了正确判别，对82.9%的交叉验证分类数据进行了正确判别，表明建立的贝叶斯判别函数较准确。重度污染、中度污染、轻度污染的贝叶斯判别函数表达式分别为：

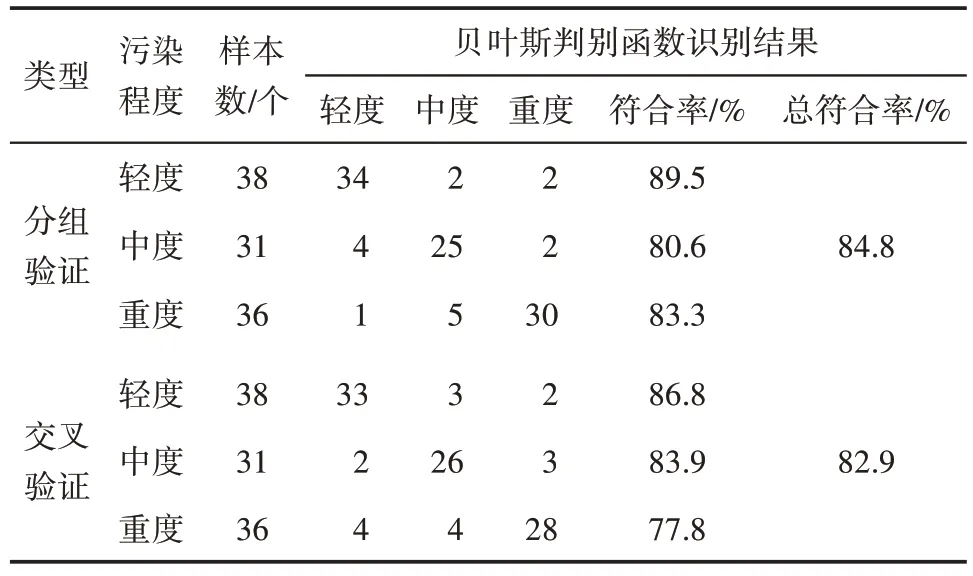
表2 储层污染判别结果Table2 Judgment results of reservoir pollution

实际运用中，通过测压资料得到测压参数，将测压参数代入贝叶斯判别函数中，可得到每一种污染程度的判别函数值，判别函数值最大者所归属类即为测压处的储层污染程度，然后采用相应的校正公式对测压渗透率进行校正，获得测压校正渗透率。

3 渗透率升尺度转换

不同来源的渗透率在表征尺度、相态方面存在差异，在数值上有所不同。岩心渗透率和测井计算的渗透率均反映的是绝对渗透率，只能反映冲洗带地层的渗透性；DST 测试得到的渗透率为油相渗透率，能反映数百米内原状地层的渗透性［24-25］。因此，需对电缆地层测试资料获得的渗透率进行渗透率升尺度转换研究［26-28］。具体步骤包括：①在DST 测试层段内，利用测压校正渗透率、岩心渗透率对测井渗透率进行刻度，此时测井渗透率为小尺度的绝对渗透率；再根据岩心分析得到的绝对渗透率与最大油相渗透率的转换关系，将测井渗透率转换为测井最大油相渗透率，完成测井渗透率的相态转换。②剔除DST 层段中非储层段对渗透率跨尺度转换的影响，对测井最大油相渗透率进行厚度加权平均，得到测井最大油相渗透率均值。③建立最大油相渗透率均值与实测DST 测试渗透率的转换关系，得到升尺度渗透率。由岩心渗透率与最大油相渗透率的关系（图4）可知，两者相关性较好，其转换模型为：

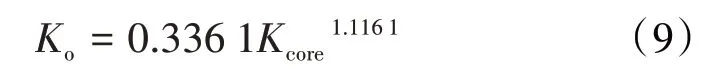
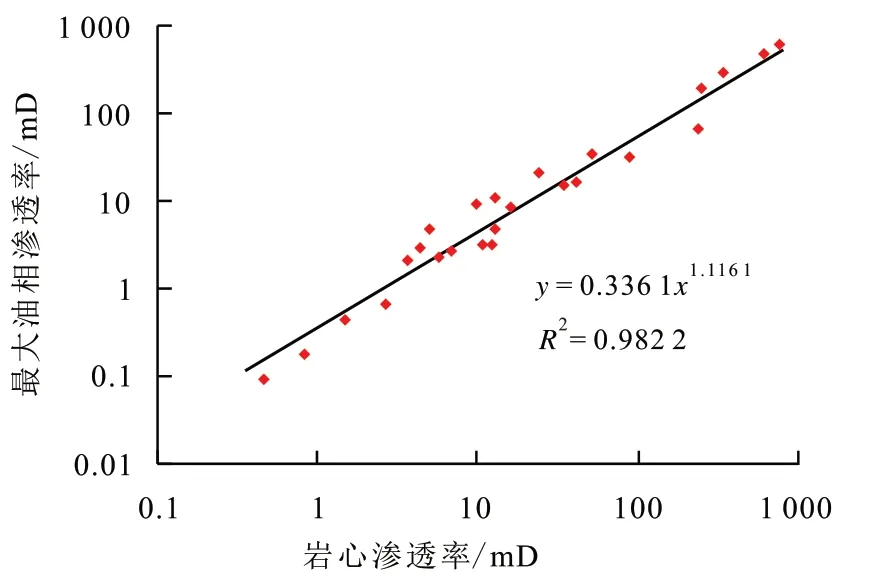
图4 岩心渗透率与最大油相渗透率关系Fig.4 Relationship between core permeability and maximum oil-phase permeability

由最大油相渗透率均值与DST 测试渗透率的关系（图5）可以看出，两者呈较好的幂函数关系，其转换模型为：

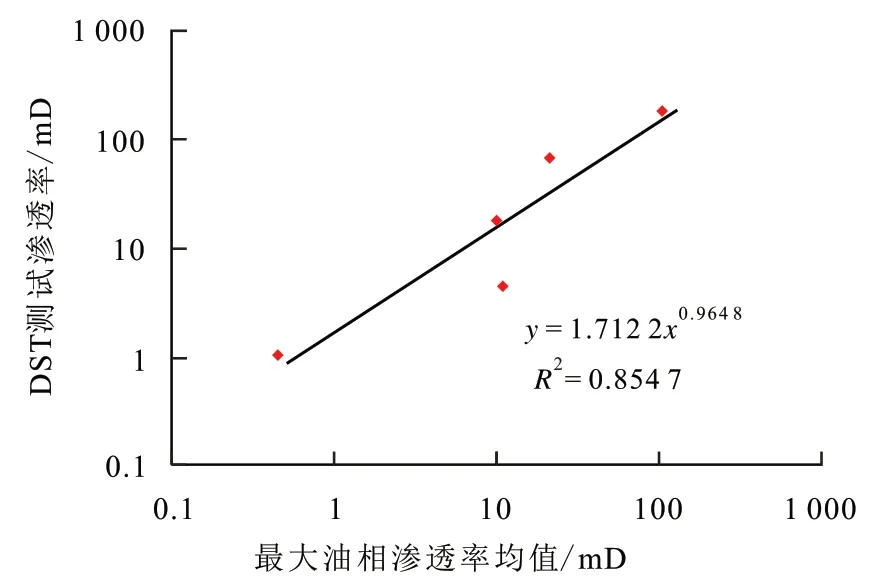
图5 最大油相渗透率均值与DST测试渗透率关系Fig.5 Relationship between maximum oil-phase permeability and DST permeability

4 应用效果

根据建立的测压资料质量评价方法和流度校正方法，对陆丰-14 井电缆地层测试数据进行了质量评价与流度校正（图6）。从图6可以看出，流度与经岩心渗透率标定的测井渗透率差距较大，在经过流度污染程度判别和污染校正后，测压校正渗透率与经岩心渗透率标定的测井渗透率较吻合。另外，测压点测压资料质量较差时，其流度受储层污染程度的影响也偏大。

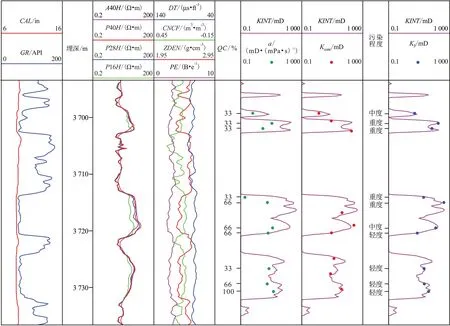
图6 陆丰-14井测压资料处理成果Fig.6 Results of pressure data processing of Well Lufeng-14

基于渗透率升尺度转换研究，利用污染校正后的测压渗透率，对已进行DST 测试的4 口井进行升尺度渗透率计算，由表3可以看出，升尺度渗透率较测井渗透率均值更接近DST 测试渗透率，相对误差在30%以内，达到行业精度要求。

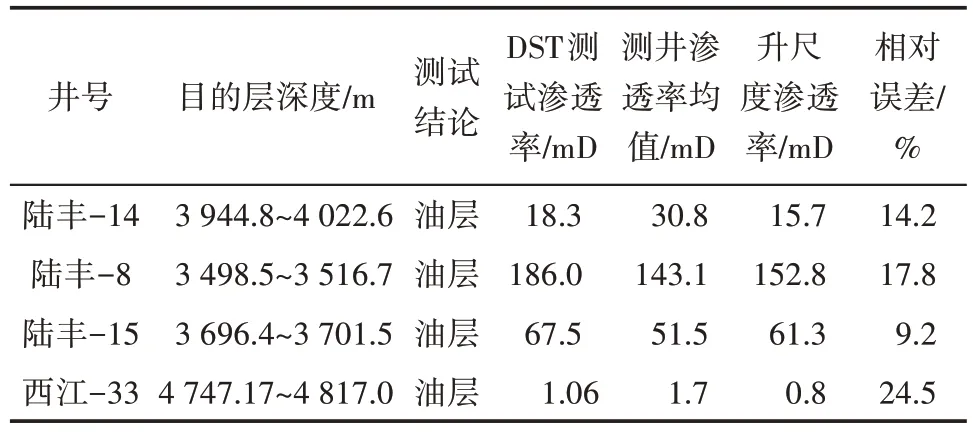
表3 升尺度渗透率计算结果Table3 Calculation results of upscaling permeability

5 结论

通过对南海东部古近系40 余口井的实际测压资料处理和系统分析研究认为：①对测压资料再处理，采用压力恢复三参数建立了测压评价质量分数，改进了测压资料的质量评价方法；分析不同仪器测压流度存在的差异，通过统一采用面积积分法计算流度消除了差异。②依据岩心资料划分了储层污染程度，建立了污染校正公式，无岩心条件下，通过测压参数利用贝叶斯判别法进行流度污染识别与校正，测压渗透率经校正后与经岩心渗透率标定的测井渗透率吻合程度显著提高。③利用电缆地层测试获得的测压校正渗透率和岩心相渗资料，以测井连续渗透率为桥梁，建立渗透率升尺度转换模型，获得的升尺度渗透率能代表储层较大范围内的渗流能力，与DST 测试渗透率更接近，相对误差在30%以内。

符号解释

a——流度，mD/（mPa·s）；

A40H——高频衰减深探测电阻率，Ω·m；

b——预测试泵速，cm3/s；

c——泥浆压力，kPa；

CAL——井径，in；

CNCF——补偿中子，cm3/cm3；

d——地层压力，kPa；

DT——声波时差，μs/ft；

e——预测试体积，cm3；

G——互相独立的样本数，个；

GR——自然伽马，API；

i1，i2，i3——测压资料质量评价的判定值；

I——污染指数；

KINT——测井渗透率，mD；

Kcore——岩心渗透率，mD；

KM——测压渗透率，mD；

KJ——测压校正渗透率，mD；

Ko——最大油相渗透率，mD；

KDST——DST测试渗透率，mD；

Komean——最大油相渗透率均值，mD；

P16H——高频相移浅探测电阻率，Ω·m；

P28H——高频相移中探测电阻率，Ω·m；

P40H——高频相移深探测电阻率，Ω·m；

PE——光电吸收截面指数，B/e；

QC——电缆地层测试测压质量评价分数；

Y1，Y2，Y3——重度污染、中度污染和轻度污染的贝叶斯判别函数；

ZDEN——地层密度，g/cm3。