长水国际机场红土动力特性室内试验研究

刘奇，符必昌，杨奚，张梅梅

(昆明理工大学国土资源工程学院，昆明 650093)

1 引言

昆明长水国际机场及岩溶洼地等区域地壳表层发育着大量的红土，其最大厚度可达20 m。红土是该区域内主要的土地资源，同时也是各类工程建设的建筑地基。现代气候条件下，红土化作用加速进行，红土裂化不断加剧，使其工程性质不断恶化。在现代气候及大规模工程活动下加剧裂化的不良工程地质问题，使昆明长水国际机场建筑物的红土地基及红土边坡存在重大安全隐患。如果已裂化红土再遭遇强烈地震，势必造成更加严重的红土土坡失稳及地基变形破坏等灾难性后果[1-4]。因此，开展昆明长水国际机场的红土动力特性的研究就显得十分重要和紧迫，该研究成果对该地区的实际工程应用具有重大指导意义。

目前，一些学者通过动三轴试验对红土动力特性进行了试验和研究并取得了相应的成果。字晓雷[5]通过动三轴试验,研究了围压对红粘土动变形特性的影响。利用双曲线模型对应力-应变关系曲线进行分析,得到了不同围压下的最大动弹性模量、最大剪切模量和阻尼比。徐鹏[6]采用SDT-20型电脑控制电液伺服双向土动三轴试验机,对饱和红土试样施加了不同的应力路径,模拟横波和纵波在不同相位差下耦合的情况,分析不同应力路径下饱和红土的动变形和动强度特性。得出随着径向循环应力幅值的变化,不同应力路径下动应变发展速度不同,应力路径斜率越大动应变发展越缓慢。骆俊晖等[7]对海口红土进行动三轴试验研究了4种因素,即固结围压、超固结比、动剪应力比、振次,对海口红土动力特性,分析了各种现象规律产生的原因，获得在一定破坏准则下的动强度。由于形成红土的条件特殊，红土种类多样，不同气候条件以及地质环境的差异使得不同地区的红土表现出的物理力学特性差别较大，从而导致相关的红土研究结果通用性不强。因此对该地区重塑红土动力特性进行研究对于指导该地区的工程经济建设以及抗震设计具有实际意义。本文将通过逐级加载的动变形试验[8-9]，研究不同固结条件对昆明长水国际机场动应力-应变关系曲线、动弹性模量以及阻尼比产生的影响。

2 实验概述

2.1 试验原理与试验土样

此次试验采用TAJ-20型土动三轴试验装置进行动三轴试验，动三轴试验是指将一定密度的圆柱体试样在轴对称应力条件下进行固结，固结完成后在不排水或排水条件下施加一定频率的循环荷载进行振动试验[10]。动三轴试验分为动变形试验和动强度试验[10]，本文主要针对动变形试验进行研究，动变形试验能确定剪切模量和阻尼比，用以计算在小变形条件下土体在一定范围内所引起的位移、速度、加速度或应力随时间的变化。

试验土样取自昆明长水国际机场红土，该区域碳酸盐岩地层(D3z、C1、C2、P1)广泛发育有岩溶。根据现场调查，该区域岩溶之上基本都覆盖有红土，研究区主要分布褐红色红土，边缘存在少量褐黄色、棕黄色红土，本文采集褐红色红土作为研究对象。昆明长水国际机场红土基本物理力学性质见表1。

表1 昆明长水国际机场红土基本物理力学性质表

2.2 试样制备及试验方案

2.2.1 试样制备

将试验用土风干碾碎后过2 mm孔径筛，测出土的最优含水率进行配土，使土样的含水率达到最优含水率之后将土搅拌均匀密封保存；按照试验的最大干密度和最优含水率来确定每层试样土质量；在制样时采用击实法制备重塑土样，根据《土工试验方法标准》[11]分5层锤击，每层土的质量相同，为了保证不出现明显的分层，还需在每层锤击完成后进行刮毛，最后制作成规格为直径39.1 mm、高度80 mm的圆柱体试样。之后将试样进行真空抽气饱和。

2.2.2 试验方案

土体所处外部环境以及其自身所具有的性质是影响土动力特性的两个重要因素。通过土的动变形试验能够得出土体应力-应变关系、动模量、阻尼比等相关结果，根据所得结果可进一步研究试验土样的动变形特性。在控制好试样含水率和质量的前提下以1Hz正弦波来研究固结围压、固结比两个因素对重塑试验土样动应力-应变关系曲线变化规律、动模量变化规律以及阻尼比特性的影响。对固结完成的试样逐级递增施加动荷载，每级加载振次为10次，对试验过程中的动应力以及动应变进行记录。详细试验方案见表2。

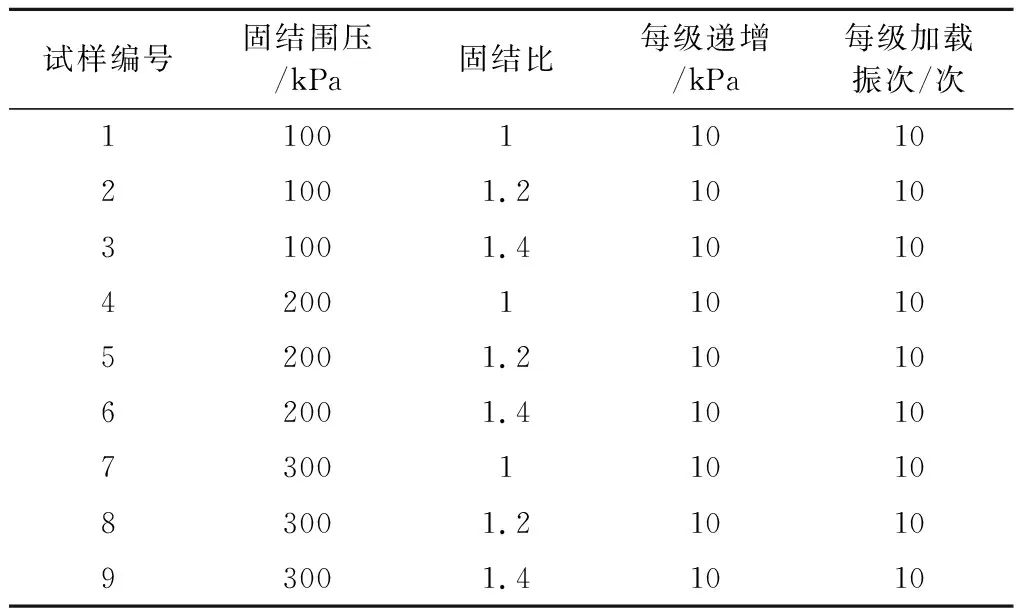
表2 红土固结不排水动变形试验方案

3 变形试验结果与分析

3.1 固结围压对动应力-动应变曲线的影响

由于固结围压的作用会使得土颗粒之间的排列状态等发生改变进而影响土的动应力和应变之间的关系。通过对试样进行相同固结比不同固结围压条件下的动变形试验，并选用较为稳定的每级荷载的第8个循环加载周期的试验数据进行处理，得出了昆明长水国际机场红土在不同固结围压下的骨干曲线，如图1。

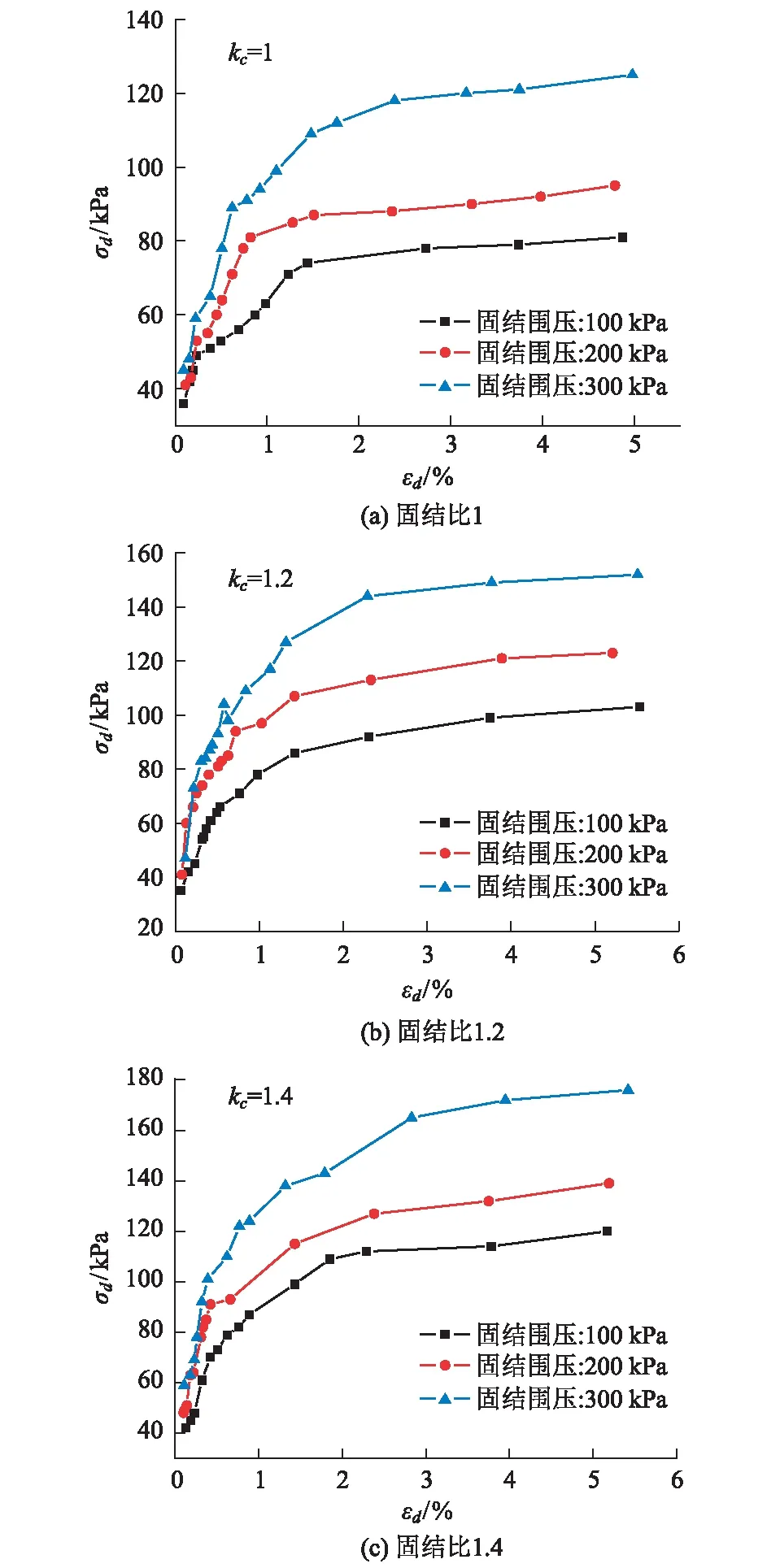
图1 不同固结围压下动应力-动应变曲线

由图1可以看出，动应力σd处在不同固结围压条件下时，会因为动应变εd的增大而呈现非线性增长的特点，且在不同固结比相同固结围压试验条件下每条曲线具有相似的变化趋势。当土体处在加载初始阶段时，动应力σd增长速度很快，但动应变εd则变化缓慢，在图1上反映为曲线具有相对较大的斜率，表明土体在加载初期，发生的动变形较小，土样仍然处于弹性变形阶段，土体结构未发生破坏，随着试验的持续进行，动应力值σd增长速度由起初的很快逐渐减缓，但是动应变值εd变化幅度则由小变大，导致曲线斜率小，这表明此时土体已经开始出现塑性变形，土体颗粒间排列开始错动，随着试验继续进行，土体颗粒之间形成的轻微错动逐渐扩大，土体破坏。进一步对比分析还可以看出，固结比一定，随着围压的增大，达到相同动应变水平时，所需要的动应力也越大，这是因为围压越大，土体横向受到约束作用越强，因而相同动应力条件下，轴向变形就会越小。此外，每条骨干曲线都存在应变转折点，应变转折点的存在正好说明土体此时正处于由弹性阶段向破坏阶段转变的过渡阶段。

3.2 固结比对动应力-动应变曲线的影响

固结比对土的动应力-应变曲线影响也很大。通过进行不同固结比条件下的动变形试验得到试验数据。对试验数据进行处理得到不同固结比条件下昆明长水国际机场红土的动应力-应变曲线，如图2。

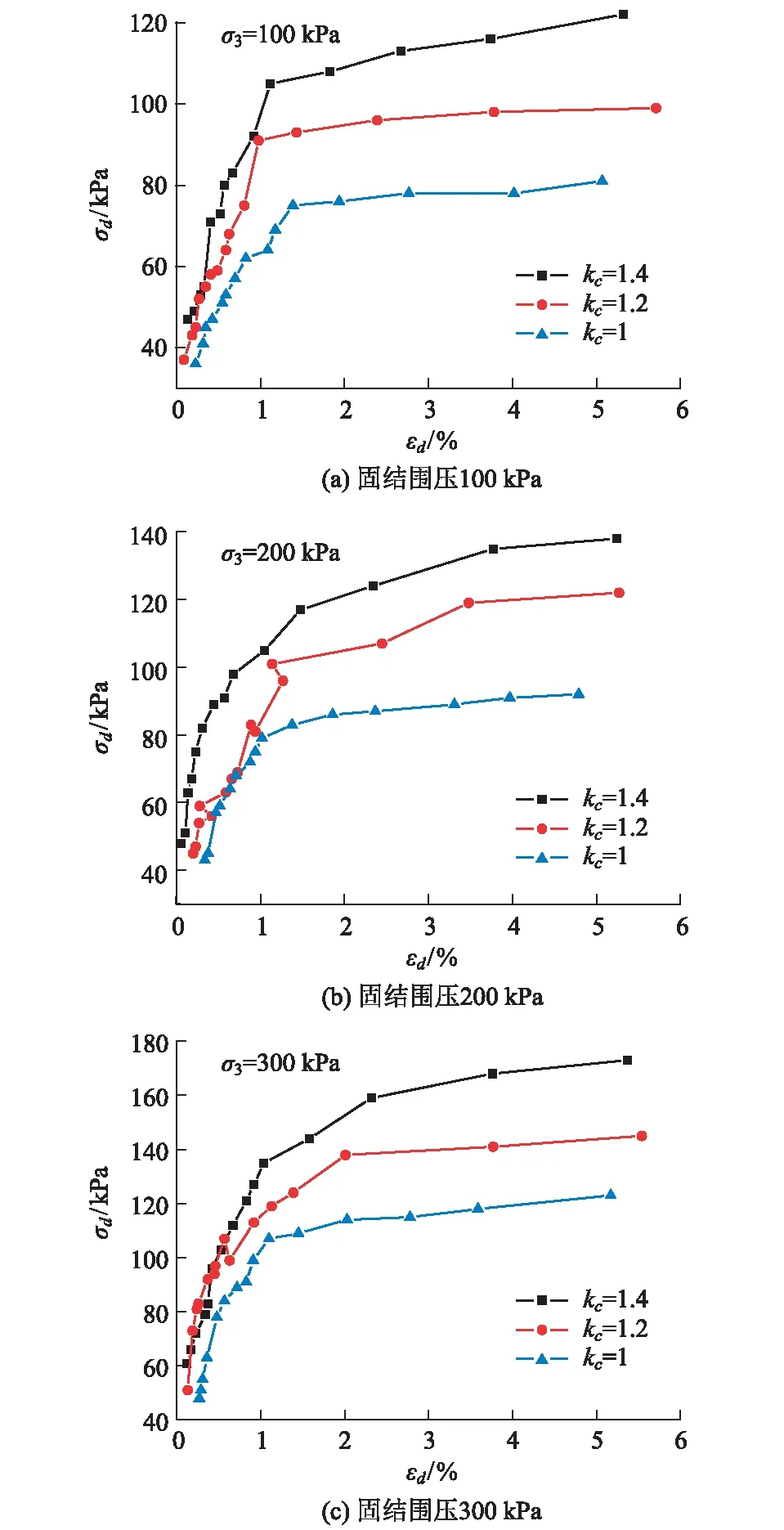
图2 不同固结比下动应力-动应变曲线

由图2可以看出，各固结比下的动应力σd随动应变εd的增大而非线性增长，且曲线的基本形态与不同围压条件下σd～εd曲线的基本形态一致。固结比对σd～εd曲线的影响与固结围压对σd～εd曲线的影响具有相同的影响特征，当固结围压相同时，固结比越大，骨干曲线距离σd轴越近。这是由于在固结围压一定的条件下，越大的固结比意味着具有越大的轴向固结应力，由此产生压密作用使得土颗粒间的相互连接越紧密，土体越不容易变形，达到相同变形所需动应力也越大。

3.3 Hardin-Drnevich模型及参数

根据前文试验结果可以看出，昆明长水国际机场红土的动应力-应变骨干曲线非线性特征明显，且基本呈双曲线型，选用目前在相关相面应用最广的Hardin-Drnevich双曲线模型进行拟合，即：

(1)

式中,σd为动应力；εd为动应变；a和b是试验参数。

由于试验条件不同，使得式(1)中参数a、b也就不同，进而导致了每条双曲线之间存在有差别。

由动弹性模量Ed的定义可知：Ed=σd/εd

(2)

若将式(1)带入式(2)并对等式两边同时求倒数可以得到：

1/Ed=a+bεd

(3)

根据式(3)可知，土体动弹性模量的倒数与动应变之间呈现线性关系。当动应变无限趋近于0时，可得到最大动弹性模量Edmax为参数a的倒数，而当动应变无限趋近于无穷时，则可得到最大动应力σdmax为参数b的倒数。

作出固结比为1，昆明长水国际机场红土在100 kPa、200 kPa、300 kPa下的1/Ed曲线以及固结围压100 kPa，固结比1、1.2、1.4条件下的1/Ed曲线，分别如图3、图4。并对1/Ed～εd关系进行拟合，结果见表3。

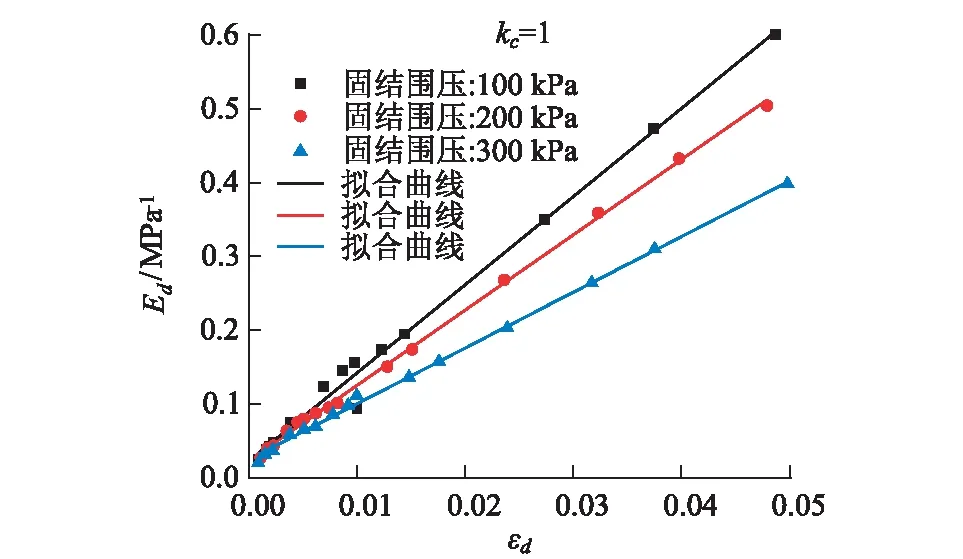
图3 不同固结围压条件下的1/Ed～εd曲线

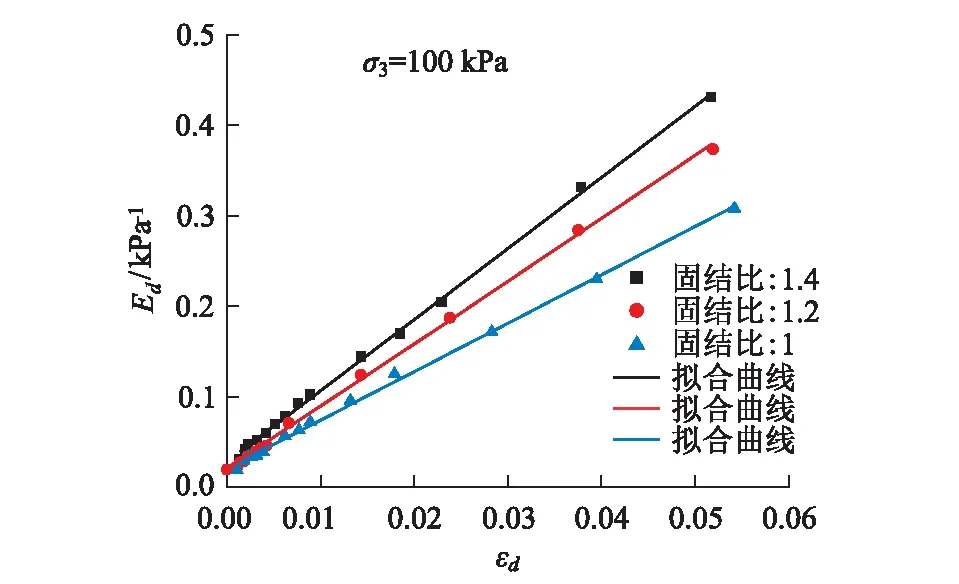
图4 不同固结比条件下的1/Ed～εd曲线

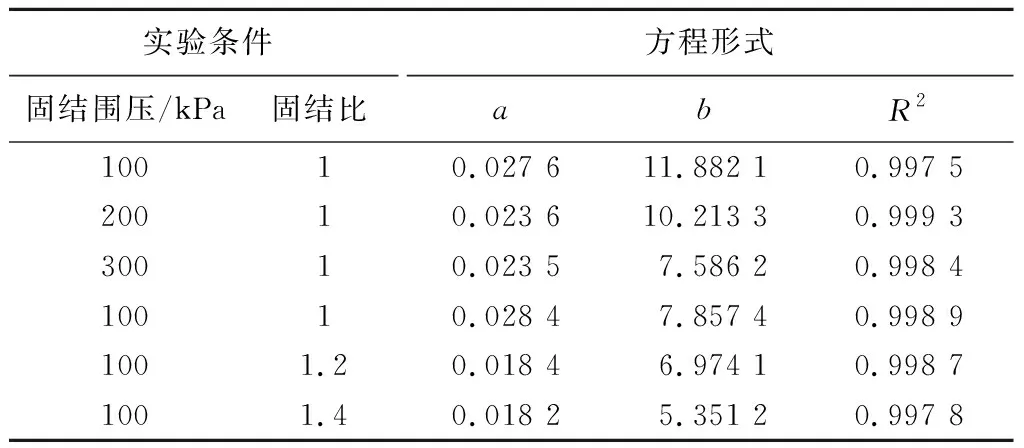
表3 不同试验条件下土体双曲线模型参数

由图3可以看出1/Ed与εd之间呈线性增加的趋势。在动应变相同情况下，固结围压越大，1/Ed越小，表明Ed越大，这是由于围压越大，土体横向变形受到约束作用越强，使得土体要产生变形就得消耗更多能量，土体也就越不容易变形。

由图4可以看出,随着εd的增大，1/Ed同样大致呈线性增大。跟图3类似，相同动应变条件下，随着固结比的增大，1/Ed反而在减小，动弹性模量Ed越大，原因是因为加大的固结比使得轴向固结应力随之加大，对土体起到压密作用，使土颗粒之间结合得越紧密，从而使得土体抵抗弹性变形和破坏的能力增强，土体也就越不容易变形。

由表3可以看出在相同固结比条件下，固结围压越大，参数a越小，参数b也越小，但参数a变化幅度很小。R2均大于0.99；同样在相同固结围压条件下，固结比越大，参数a越小，参数b也越小。R2同样均大于0.99，可以得知对图中曲线进行线性拟合是完全可行的，试样用红土的动应力-应变关系曲线符合Hardin-Drnevich双曲线模型。

3.4 试验红土动模量分析

动弹性模量是与土体变形特性相关的重要基本参数，其变化可以反映出土体在动力作用下变形的发展规律，因此研究土的动弹性模量对研究土体变形特性具有重要意义。土体处在循环加载初期时，仍然具有很大的刚度，因此动应变变化很慢，可认为土体正处于弹性变形阶段，此时土体的动弹性模量被称为最大动弹性模量。由Edmax=1/a,σdmax=1/b,在控制固结比为1不变的条件下，根据表3可得围压100 kPa、200 kPa、300 kPa时的Edmax和σdmax，如表4。

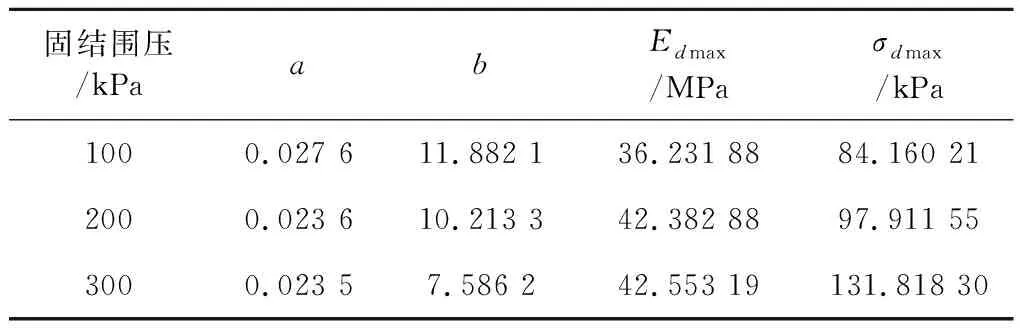
表4 最大动弹性模量和最大动应力

由表4可以看出在固结比一定的条件下最大动弹性模量和最大动应力均增大，但由于最大动弹性模量很难通过动三轴试验直接得出，可通过Janbu在1963年提出了围压σ3c或平均应力σm=(σ1c+2σ3c)/3与动模量Ed表现为增量关系，但此关系使用范围有限，主要适用于Kc=1且σ3c=σm时，依据Janbu的研究，就能确定在满足前提的情况下的每一个σ3c所对应的最大动弹性模量，表示为式(4)：

(4)

式中，Edmax为最大动弹性模量；k为拟合直线的纵截距，n为拟合直线的斜率;Pa为为标准大气压数值(101.325 kPa)。

本文采用式(4)回归方程对昆明长水国际机场红土在Kc=1条件下的最大动弹性模量Edmax进行拟合处理，拟合结果为：k=340.68，n=0.316 1，根据结果可以得到Edmax～σ3c关系如图5。由图5可知在相同固结比条件下Edmax～σ3c呈线性增长关系，在围压100 kPa时Edmax接近于34 MPa，围压200 kPa时Edmax接近于43 MPa，围压100 kPa时Edmax接近于48MPa，这与经过动三轴试验并通过Edmax=1/a计算结果相近且R2为0.989 32，说明拟合情况较好。

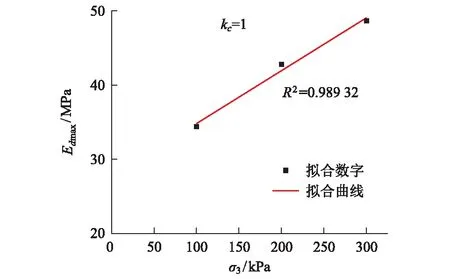
图5 不同围压条件下Edmax～σ3c关系图

3.5 试验红土阻尼比分析

阻尼比是由于循环加载过程中土颗粒之间的相互摩擦、挤压等作用使土体能量不断耗散而产生的。在土动力学中[12]，将实际阻尼系数和临界阻尼系数的比值称为阻尼比，它是反映土体在动荷载作用下，一个周期内损耗的能量与作用的总能量的比，是土动力学的一个重要指标，同时也是进行动力反应分析时必不可少的参数。在计算阻尼比时，可根据式(5)进行计算。

(5)

式中，λ为阻尼比;ΔW近似为滞回圈的面积;W近似为三角形OAA′的面积，如图6所示。

图6 滞回圈与阻尼比

3.6 固结围压对阻尼比的影响

在频率1 Hz、固结比=1、含水率36%不变的情况下，通过控制不同的固结围压进行动变形试验，得到试验数据。对试验数据进行处理，得到不同围压条件下昆明长水国际机场红土的λ～γd散点图，如图7。

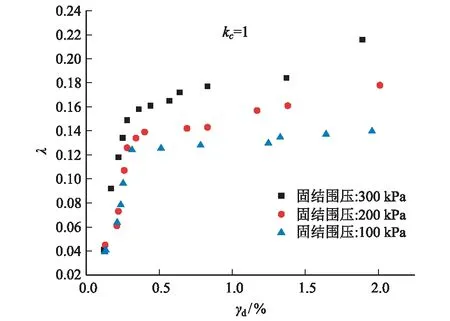
图7 不同固结围压条件下的λ～γd散点图

由图7可以看出，不同固结围压条件下λ～γd散点呈非线性增长，在初始γd很小的阶段，不同固结围压条件下的λ增长变化基本一致，且增幅较大，增长速率较快，持续到γd大约为0.32%时，开始放缓，此时固结围压为100 kPa、200 kPa、300 kPa时的λ分别为0.123、0.133、0.158，散点出现这种趋势的原因是由于：当在加载初期时，γd累积较小，此时试样土颗粒之间未充分接触，摩擦力较小，发生位移所消耗的能量较小，λ也就相对较小，土体的累积变形小，而使得内部结构相对稳定。之后土体被迅速压密，土颗粒间摩擦力突然增大，发生位移所消耗的能量迅速增多，阻尼比变大。随着加载次数和级数的增大，动应力累计水平增大，土体自身累计变形较大，造成土颗粒结构逐渐破坏。此时，土颗粒间的摩擦力虽然仍在增大，但由于土颗粒间结构的逐渐破坏，使得增大放缓，表现出来消耗的能量耗散速度减缓，因此阻尼比随动剪应变的增大而增大的速率变平缓。在将不同固结围压下的λ～γd散点图进行比较，可以看出，固结围压越大，其阻尼比也越大，作用相同过程所消耗的能量也越大。

3.7 固结比对阻尼比的影响

在频率1 Hz、固结围压100 kPa、含水率36%不变的情况下，通过控制不同的固结比进行动变形试验，得到试验数据。对试验数据进行处理，得到不同固结比条件下昆明长水国际机场红土的λ～γd散点图，如图8。

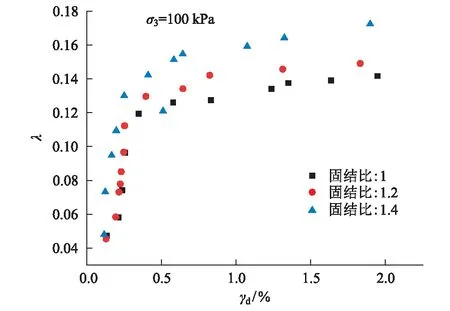
图8 不同固结比条件下的λ～γd散点图

由图8可以看出，不同固结比条件下λ～γd散点呈非线性增长，趋势基本与不同固结围压下的散点趋势一致。大约在γd为0.375%时，散点斜率开始减小，此时固结比为1、1.2、1.4的λ分别为0.126、0.121、0.142，此后3条散点之间的间距(λ差值)近似维持在0.1左右。观察可知，当其他条件一定时，在达到相同γd时，固结比越大，λ也越大。这是因为在固结围压一定的条件下，固结比越大，初始偏应力也就越大，土颗粒间的相互连接也越紧密，就使得土颗粒之间连接变松散所需耗散的能量越大，即阻尼比越大。

由图7及图8可以看到，在达到相同γd时，不同固结围压条件下的λ值比不同固结比条件下的λ值偏大，且在散点曲线斜率开始减小后，不同围压条件下散点曲线之间的间距大于不同固结比条件下散点曲线之间的间距，由此可知，固结围压对λ～γd的影响比固结比大。

4 结论

通过对昆明长水国际机场红土动变形特性的研究得出下列结论：

(1) 在动力荷载作用下，可将红土的动应力-应变的发展分为3个阶段：分别为近似弹性变形阶段，塑性变形阶段，土体产生破坏阶段。动应力-应变骨干曲线明显呈非线性变化，控制其他条件不变，固结围压和固结比对骨干曲线的影响均相同，均是在固结围压或固结比越大，试样达到相同动应变时所需要的动应力越大。

(2) 在相同的应变条件下，红土的动弹性模量随着固结围压增大而增大；随着动弹性应变的不断增大而不断减小。

(3) 在相同的应变水平下，阻尼比会随着固结围压和固结比的增大而增大。且不同围压条件下散点曲线之间的间距大于不同固结比条件下散点曲线之间的间距，得出固结围压对阻尼比的影响比固结比大。