煤岩裂隙高位注浆浆液扩散规律

戚绪尧，王 涛，陈良舟

(1.中国矿业大学 煤矿瓦斯与火灾防治教育部重点实验室，江苏 徐州 221116；2.中国矿业大学 安全工程学院，江苏 徐州 221116)

煤炭在相当长时间内仍是我国能源结构的主要部分。深部煤炭资源开采及老旧采区复采是拓展煤炭资源、保障煤炭供应的有效途径。随着大规模高强度的回采和深部开采活动的进行，巷道顶板或再生顶板中顶部煤岩体在采动应力或冲击地压下易破裂产生裂隙，随着裂隙的进一步扩展，易发生裂隙漏风及顶板失稳等风险，从而引发诸如顶板或再生顶板垮落、再生顶板遗煤自燃、高冒区遗煤自燃等重大安全问题。

钻孔注浆是封堵裂隙和加固煤岩体的主要手段之一，浆液在裂隙通道内的流动特性是注浆施工设计的重要参考指标。由于裂隙注浆属于强隐蔽性的过程，煤矿井下难以实时监测浆液的流体力学参数，现场注浆设计一般依据注浆理论。但注浆理论的发展滞后于现场需求，特别是针对上覆煤岩裂隙的高位注浆，由于应力消失后煤岩裂隙的扩散逐步停止，此时的煤岩裂隙属于有界的裂隙空间。现有注浆理论难以适用于有限裂隙空间内的高位注浆，导致现场注浆设计大多凭经验设计，具有较大的盲目性，因此开展煤岩裂隙高位注浆模型研究具有重要的工程意义。

国内外学者主要从理论模型、模型实验和数值模拟方面对裂隙岩体内注浆浆液流动规律进行了大量研究。在理论模型方面，由于裂隙网络分布的复杂性，解析解主要集中于单裂隙的通道流和径向流中。基于润滑近似的假设，部分学者推导了不同流变特性流体在单裂隙中的流动解析解，如LI等推导了变密度聚合物浆液在平面裂缝中的径向瞬态流动的解析式；MAJIDI等推导了屈服幂律流体在平板裂隙间的径向流动理论解，并通过数学简化，给出了近似解析式；ZOU等分析了Bingham流体径向流动解析式，并从力平衡的角度推导了塞流区合理的表达式；MOHAMED等系统地推导了非线性牛顿流体在恒压、恒流量和恒能量3种工况下的平板裂隙通道流和径向流的解析式；王东亮等基于不同流体的本构方程及运动方程，推导了不同流型浆液的扩散方程。HU等建立了幂律流体在倾斜管状裂隙中扩散的解析式，并分析了裂隙倾角等因素对浆液扩散距离的影响；裴启涛等建立了恒速率注浆条件下反映浆液黏度时空变化的倾斜裂隙注浆扩散模型。李术才等建立了单一平板优势劈裂注浆扩散模型，推导了考虑浆液流变特征的优势劈裂注浆扩散控制方程。上述研究成果在一定程度上推动了注浆理论发展，但未考虑有限裂隙空间中裂隙边界对浆液流动状态的影响，限制了在煤岩体裂隙高位注浆施工设计中的应用。

模型试验和数值模拟广泛应用于理论模型验证以及探究复杂流动。模型实验中数据的获取依赖于传感器的铺设，对复杂裂隙流动模型实验难以获取全局的流体力学参数。与模型实验的局限性相比，数值模拟只需给出合理的本构模型、边界条件和计算参数便可得到更精确的全局解，因此数值模拟逐渐成为探究裂隙注浆规律的重要手段。

综上，现有裂隙注浆研究主要侧重于无限延伸单裂隙内流动的解析解和裂隙网络中的数值解，对高位注浆和裂隙侧壁对浆液流动影响研究较少。笔者在分析高位注浆工艺和浆液流变特性的基础上，建立了任意倾角下有限边界裂隙注浆扩散数学模型，然后通过对数学模型进行数值计算探究了不同裂隙倾角和注浆速率下裂隙高位注浆中浆液的扩散形态、流量及压力场变化规律。基于数值计算结果，建立了浆液高位流动数学模型，给出了恒定注浆速率工况下的解析解，并对解析解的合理性进行了验证，以期为煤矿井下煤岩裂隙灾害治理过程中高位注浆工艺设计提供一定的理论参考。

1 煤岩裂隙高位注浆理论

1.1 注浆工艺

裂隙注浆工艺主要包括恒定流量注浆、恒定压力注浆及恒定能量注浆，不同的注浆工艺对浆液在裂隙流动过程中流动规律影响显著。井下通过注浆管将浆液泵送至裂隙煤岩体内部对裂隙空间进行填充，而顶部的煤岩裂隙体属于易碎结构，在承受较大钻孔压力和注浆压力时易发生垮塌。为避免过大的初始注浆压力破坏煤岩裂隙结构，针对高位注浆时宜采用恒定流量注浆工艺。在恒定流量注浆工艺下，注浆压力将会随着浆液的扩散距离逐步增加，直至达到高位煤岩所能承受的最大压力。因此，本文的模型推导和数值建模均采用恒定的注浆速率边界条件。

1.2 浆液流变方程

井下煤岩裂隙的注浆介质以非牛顿流体为主，包括凝胶、泡沫、黄泥浆、水泥等及其几种介质的混合物。由于非牛顿流体的流变性能在裂隙渗流过程中的变化是非线性的，为有效控制注浆介质的流动范围，通常在注浆设计时通过改变注浆介质内材料的配比来调整介质的整体流变特性。本文以满足Bingham流变模型的浆液作为研究对象，其流变模型可描述为

(1)

式中，为剪切应力，Pa；为屈服应力，Pa；为黏度，Pa·s；为流速，m/s；为垂直流体流动方向。

1.3 浆液流动方程

基于Bingham流体流变特性，以倾斜有限边界的光滑平板裂隙为研究对象，则浆液在裂隙中流动的物理系统如图1所示(其中，为裂隙开度，m；为塞流区高度的一半，m；为注浆孔半径，m；为注浆孔出口压力，Pa；为裂隙倾角，(°))。

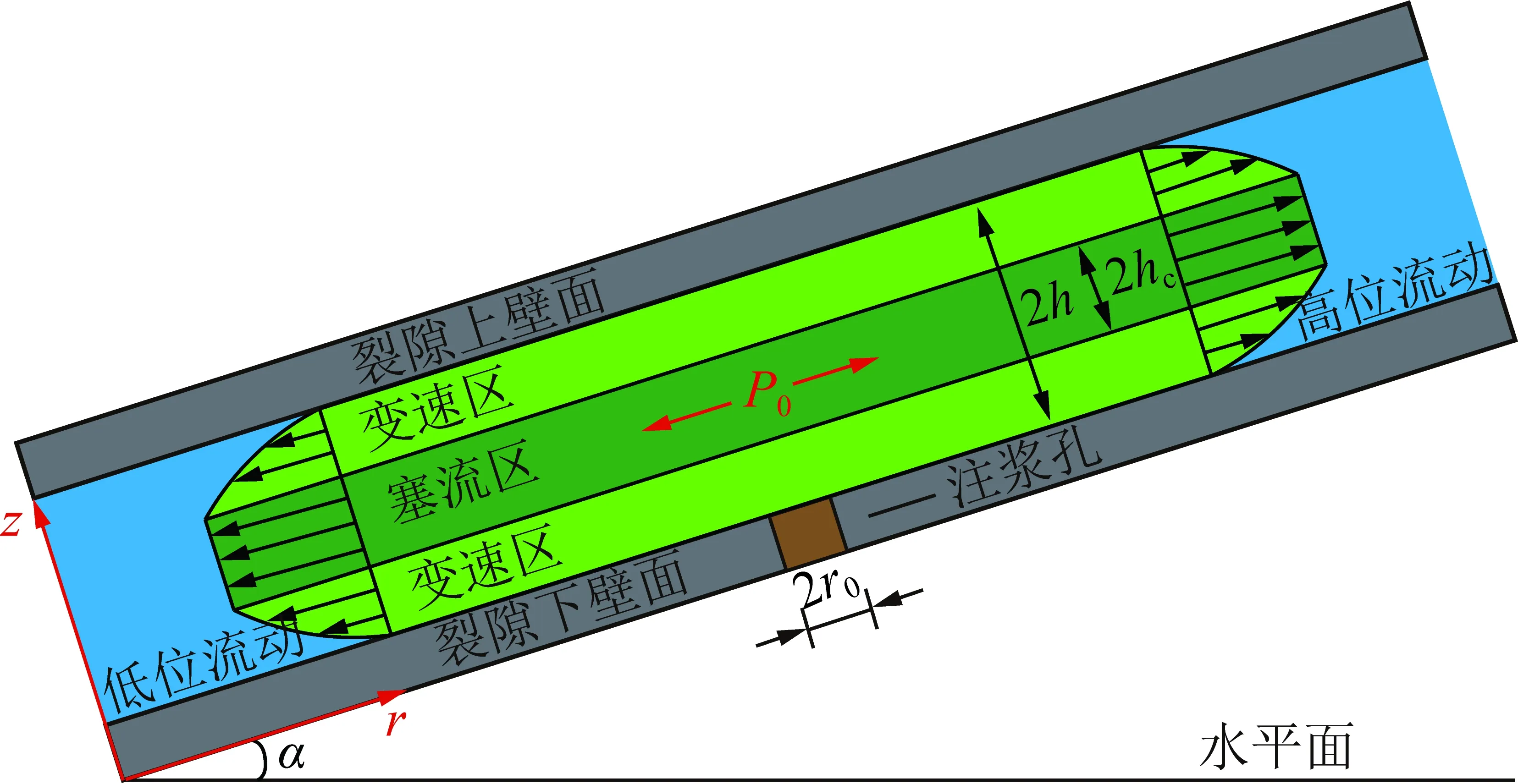
图1 浆液在倾斜裂隙内流动示意Fig.1 Illustration of slurry flow in inclined fracture

由图1可知，浆液自注浆管流出进入裂隙空间后沿裂隙扩展方向径向流动，由于裂隙存在倾角，浆液流动方向可分为克服重力方向沿裂隙壁面向上的高位流动和趋于重力方向沿裂隙壁面向下的低位流动。为描述上述物理系统，在建立数学模型前，做出以下基本假设：① 裂隙形态不随注浆过程变化；② 浆液在裂隙壁面上满足无滑移条件；③ 浆液视为各向同性的均质不可压缩流体，满足连续介质假设描述；④ 浆液的流动只发生在裂隙空间内。

满足连续介质假设的流体在流动过程中可由连续性方程和动量方程描述。基于润滑近似，考虑浆液自注浆管流出后沿裂隙通道径向流动，在柱坐标系下裂隙空间内浆液所满足的控制方程可简化为

(2)

式中，为压力，Pa；为剪切应力，Pa；为高位流动扩散距离，m；为低位流动扩散距离，m；为重力加速度，m/s；为流动密度。

控制方程的边界条件有

(3)

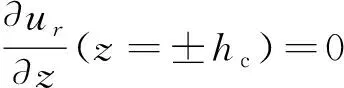
(4)

(=)=,(=)=

(5)

式中，为轴方向上的流速，m/s；为浆液最终扩散距离，m；为浆液扩散锋面前端压力，Pa。

基于平板单裂隙注浆扩散常规解法，结合塞流区高度的半经验公式，分别对式(2)中高位流动和低位流动表达式进行多次积分，可得高位流动和低位流动流量为

(6)

式中，为高位流动流量，m/s；为浆液高位流动扩散锋面弧长；为低位流动流量，m/s；为浆液低位流动扩散锋面弧长。

浆液扩散过程中注浆总流量为

=+

(7)

其中，为注浆总流量，m/s。由此可分别得出高位流动和低位流动过程的压降为

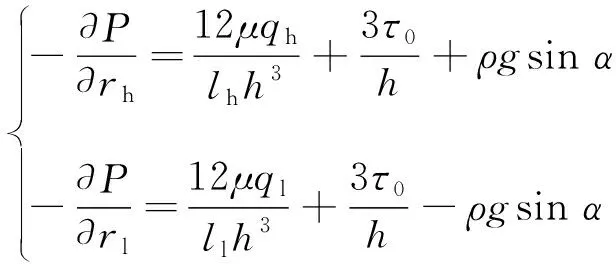
(8)

2 裂隙高位注浆数值模拟

2.1 数值模型建立

由式(8)可知，浆液流动方程中包含浆液不同流动方向上的压降和扩散锋面弧长2类未知项，因此难以得出基于上述基本假设下的解析解。为探究浆液在高位裂隙空间内的流动规律，采用数值模拟对上文中的控制方程进行数值求解。在上述基本假设前提下，建立有限边界裂隙高位注浆数值模型，其几何模型及局部网格如图2所示。

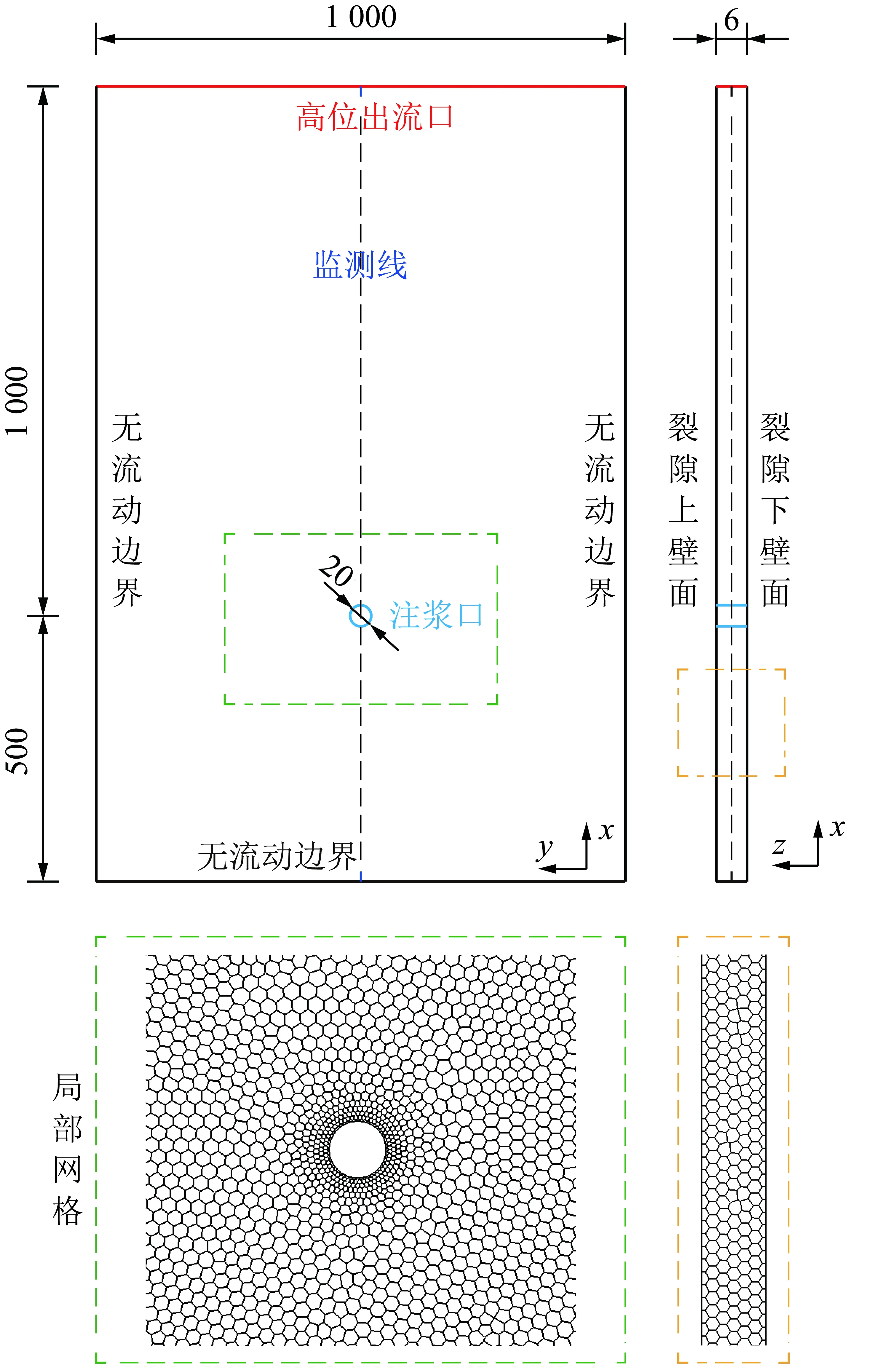
图2 几何模型及局部网格Fig.2 Geometric model and local grid

由图2可知，数值模型中注浆孔为入流口，设置为速度入口边界，注浆速率设定为0.05，0.10，0.20 m/s三种工况。高位出流口为出口，设置为压力出口边界，出口压力为0。其余面均设置为壁面，且满足壁面无滑移条件。浆液的物性参数设置需介于井下常用注浆介质物性参数的合理范围内，为不失一般性，数值模型中浆液的密度设为1 300 kg/m，塑性黏度设为5 Pa·s，屈服应力设为5 Pa。通过改变数值模型中不同坐标方向的重力加速度分量实现不同倾斜角度下的流动模拟，分别设置15°，30°，45°，60°，75°五个倾斜角度的计算工况。同时，为定量对比流域内关键位置流体力学参数变化规律，在模型中设有监测线。注浆是浆液对裂隙空间内原生介质(空气、水等)驱替的过程，本模型中的原生介质为空气，初始时刻裂隙内空气体积分数为1。为捕捉浆液在裂隙中扩散锋面的变化规律，使用VOF模型计算气液交界面。使用ANSYS FLIENT 15.0软件进行数值计算，压力-速度耦合项使用PISO算法，空间离散化中压力项采用PRESTO!算法，动量项采用二阶迎风格式，体积分数项采用CICSAM算法，时间步长设置为0.01 s。数值模型采用多面体网格进行离散，为避免网格数量对结果造成的误差，进行了网格无关性验证。以倾角30°、注浆速率0.10 m/s计算工况下注浆50 s和100 s时的压差作为检验指标，通过改变面网格尺寸及裂隙开度方向上的网格层数设置5组计算网格，计算结果如图3所示。由图3可知，当网格数量超过30万后，压力值的增速放缓，且随着网格数量的增加相对误差大幅下降。综合考虑计算效率和误差，选取第3组网格进行数值计算，该套网格的网格数量为305 188。

图3 网格无关性验证Fig.3 Grid independence verification

2.2 模拟结果及分析

2.2.1 扩散形态分析

分别以注浆速率为0.1 m/s和倾角为30°的计算工况为例，分析倾角和注浆速率对浆液在裂隙空间内扩散规律的影响。取裂隙开度中心(=0.003 m)的计算结果作为参考结果，数值模拟注浆过程中浆液的扩散形态如图4所示。

图4 数值模拟注浆扩散形态Fig.4 Numerical simulation of grouting diffusion pattern

由图4可知，以与注浆口中心水平对齐的黄色虚线为界，虚线上方的流动为高位流动，虚线下方的流动为低位流动。根据高位流动和低位流动扩散锋面的变化规律，可将浆液在裂隙内的流动过程划分为3个阶段：自由扩散阶段、过渡阶段和受限堆积阶段。在自由扩散阶段，浆液整体扩散形态呈圆形，受重力作用影响，低位流动趋势大于高位流动，整体扩散形态的圆心随流动时间的延长逐渐下移转变为椭圆形，直至低位流动的扩散锋面前端与裂隙底部接触时停止。在过渡阶段，受裂隙底部壁面支撑作用，浆液整体扩散形态逐渐由椭圆形转变为“n”形。该阶段内低位流动在底部壁面的支撑作用下向两侧壁面扩散，同时高位流动锋面逐渐延展，弧度逐渐变大，形状由半圆形向矩形过渡。在受限堆积阶段，底部空间均被填充，低位流动已经结束，在底部和两侧壁面的限制下，浆液流动以高位流动为主，整体扩散形态由“n”形转变为类矩形。在此过程中，高位流动的扩散锋面已经稳定不再随扩散的距离而改变。

由图4(a)可知，在任意倾角下，浆液的扩散形态演变规律相同，倾角大小对自由扩散阶段和过渡阶段影响较大，对受限堆积阶段影响较小。倾角越大，浆液完成自由扩散阶段和过渡阶段的时间越短。这是因为越大的裂隙倾角使浆液在低位流动时所分配的重力分量越大，浆液的扩散以低位流动为主，浆液率先完成底部区域充填。在底部区域填充完毕后，浆液以高位流动为主，该阶段内浆液流动趋于稳定，锋面与形态不再发生变化。图4(a)中相同注浆时间下浆液在倾角60°和75°时的扩散形态基本一致，这是因为倾角增大到一定程度后，重力分量的增幅开始减缓，低位流动趋势逐渐达到阈值，对高位流动的影响也逐渐减小。由此可得出，裂隙倾角对浆液扩散形态的影响程度随着裂隙倾角的增大先增强后减弱。

由图4(b)可知，注浆速率对浆液流动阶段的转变速度具有显著影响，注浆速率越大，完成流动阶段转变的时间间隔越小。在注浆初期，不同注浆速率下的浆液均处于自由扩散阶段。但随着注浆时间的延长，注浆速率大的浆液率先完成过渡阶段并进入受限堆积阶段。由此可得出，注浆速率对浆液扩散形态的影响程度随着注浆时间的延长逐步加强。

取浆液体积分数大于0.5的区域作为浆液扩散区域，以浆液扩散锋面最前沿处的距离作为浆液的扩散距离，监测线上不同工况下高位流动的扩散距离随时间变化曲线如图5所示。

图5 高位流动扩散距离变化曲线Fig.5 Variation curves of high-position flow diffusion distance

由图5可知，整体上浆液高位扩散距离随着注浆时间的延长逐步增加，在不同倾角和注浆速率下，浆液高位扩散距离的增速不同。注浆速率0.05 m/s时，注浆64 s后浆液在15°，30°，45°，60°，75°裂隙中高位扩散平均流速分别为0.003 00，0.002 26，0.001 73，0.001 42，0.001 27 m/s；注浆128 s后，浆液在15°，30°，45°，60°，75°裂隙中高位扩散平均流速分别为0.000 959，0.000 587，0.004 33，0.000 371，0.000 309 m/s；注浆192 s后，浆液在15°，30°，45°，60°，75°裂隙中高位扩散平均流速分别为0.000 80，0.000 77，0.000 99 ，0.001 14，0.001 27 m/s。表明在相同流动阶段内，随着裂隙倾角的增大，浆液高位流动扩散增速逐渐降低，但增速下降幅度随着倾角的增大逐渐减小，尤其是在受限堆积阶段，裂隙倾角的差异对高位扩散距离增速的影响程度显著低于自由扩散阶段和过渡阶段，这与扩散锋面受重力分量变化影响的规律一致。由此可得，裂隙倾角对高位扩散距离的影响程度随着流动阶段的演化逐渐减小。

裂隙倾角30°时，在0.05，0.10，0.20 m/s工况下，注浆32 s后浆液平均流速分别为0.003 6 ，0.004 7，0.008 8 m/s；注浆64 s后分别为0.000 55，0.002 20，0.003 50 m/s；注浆96 s后分别为0.000 93，0.001 40，0.009 90 m/s。表明在相同注浆时刻注浆速率对高位扩散增速的影响随着注浆速率的增大而增加。在不同注浆时刻注浆速率对高位扩散距离增速的影响程度，随着注浆时间的延长先增加后减小，但当浆液进入受限堆积阶段后，注浆速率变化对高位扩散距离增速开始逐步增大。由此可得，注浆流速对高位扩散距离的影响程度随着流动阶段的演化逐渐增大。

2.2.2 流量分析

根据数值模型中注浆口的几何特征，在恒定注浆速率下，理论上一定时间内从注浆口流入裂隙空间内的总体积等于在该注浆时间段内浆液在裂隙空间内填充体积，即

==2π=+

(9)

式中，为从注浆口注入裂隙空间总体积，m；为注浆时间，s；为高位流动的体积，m；为低位流动的体积，m；为注浆速率。

为定量分析高位流动和低位流动在不同流动阶段的流量分配规律，定义高位流动的分流系数为

(10)

分流系数表征在任意时刻注入裂隙空间的浆液中高位流动流量占比，不同工况下分流系数随流动时间的变化曲线如图6所示。

由图6可知，浆液整体分流系数随注浆时间的延长迅速减小，当减小到最低点后开始迅速增大直至分流系数达到1后保持不变。结合浆液不同的流动阶段分析可知，在自由扩散阶段，浆液受重力分量影响高低位不均衡扩散，此阶段内低位流动占据优势，浆液率先充填底部空间，表现为分流系数逐渐减小。当低位扩散距离到达裂隙底部时，低位扩散趋势达到最大值，对应分流系数达到最小值，此后低位流动开始向四周蔓延进入过渡阶段，此阶段开始低位流动逐渐消失，表现为分流系数开始逐步增大，表明该阶段高位流动趋势开始增强。当低位空间被填充完毕后，浆液进人入高位堆积阶段，此时低位流动已结束，表现为分流系数迅速增大直至达到峰值1，并保持峰值不变，表明在高位堆积阶段只存在高位流动，此阶段内注浆管所注入的浆液体积均为高位流动增加的体积。

图6 分流系数变化曲线Fig.6 Variation curves of shunt coefficient

0.10 m/s工况时，在倾角15°裂隙内，分流系数在注浆88 s后达到最小值0.337，176 s后达到最大值1；在倾角30°的裂隙内，分流系数在注浆64 s后达到最小值0.219，136 s后达到最大值1；在倾角45°裂隙内，分流系数在注浆56 s后达到最小值0.144，128 s后达到最大值1；在倾角60°裂隙内，分流系数在注浆48 s后达到最小值0.101，120 s后达到最大值1；在倾角75°裂隙内，分流系数在注浆46 s后达到最小值0.083，118 s后达到最大值1。可知裂隙倾角越大，分流系数的最小值越小，达到最小值和最大值的时间越短，表明过大的裂隙倾角加大了高位流量的损耗，并加快了流动阶段的转变。

裂隙倾角30°工况下，0.05 m/s注浆速率时，分流系数在注浆96 s后到达最小值0.123，256 s后达到最大值1；0.20 m/s注浆速率时，分流系数在注浆40 s后到达最小值0.312，88 s后达到最大值1。 由此可知，注浆速率越大，分流系数的最小值越大，达到最小值和最大值的时间越短，表明过大的注浆速率减缓了高位流量的损耗，并加快了流动阶段的转变。

..压力场分析

以监测线上压力值时空变化结果作为浆液流动方向上压力场变化的参考结果，倾角15°，75°工况下监测线处压力场分布如图7所示。

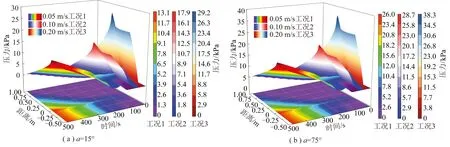
图7 监测线处压力场分布曲面Fig.7 Pressure field distribution surface at monitoring line

由图7可知，整体上监测线处压力值随着流动时间的延长而逐渐增大，在监测线不同距离处压力的增幅有所差异。注浆口处压力值最大，并随着注浆时间的延长向四周衰减，由于出口边界设置为零压出口，因此在浆液未覆盖区域相对压力始终为0。而低位扩散区域受底部支撑作用导致浆液堆积，因此低位区域压力值随注浆时间延长逐渐增大。分析图7中不同倾角的工况可知，裂隙倾角的增加加大了扩散相同距离所需的注浆压力，注浆压力随倾角的增长呈非线性变化，在初期自由扩散阶段注浆压力随裂隙倾角的变化不明显，而在高位堆积阶段的增幅产生较大差异。同时，过大的裂隙倾角也加大了裂隙底部区域的压力值，裂隙倾角越大，底部区域压力值增幅越大。分析图7中不同注浆速率工况可知，注浆速率显著改变了曲面幅度，即注浆速率越大，相同扩散距离处的压力值也越大。

将注浆口处压力视为注浆压力，不同工况下注浆压力随时间变化规律如图8所示。

图8 注浆压力变化曲线Fig.8 Variation curves of grouting pressure

由图8可知，整体上注浆压力随注浆时间的延长而缓慢增加，但不同流动阶段的变化趋势不同。在自由扩散阶段和过渡阶段的注浆压力增幅较小，整体波动不大。当浆液进入受限堆积阶段后，注浆压力开始发生突变，压力值迅速增大。同时，不同裂隙倾角和注浆速率对不同阶段的注浆压力影响不同，注浆速率和裂隙倾角的增大均会导致注浆压力增加，但倾角大小在自由扩散阶段和过渡阶段对注浆压力的影响程度较小，在浆液进入受限堆积阶段后产生明显差异，这与倾角对高位扩散距离的影响规律不同。注浆速率对初始注浆压力影响较大，且同样在浆液进入受限堆积阶段后发生突变。

3 浆液高位流动数学模型

3.1 模型求解

通过数值模拟，可得出浆液在倾斜裂隙空间内浆液扩散锋面的变化规律，以及流动方向上的压力场和流量分配规律，但数值模型建模过程复杂，计算结果难以反映物理量之间的量化关系。由煤岩裂隙结构性质和高位注浆工艺可知，注浆管难以向上伸入高位裂隙深部区域，因此浆液在倾斜裂隙内的低位流动空间有限。为此，以高位流动为研究对象，建立注浆浆液高位流动数学模型，探究浆液向高位裂隙深部流动过程中各流体力学参数变化规律对高位注浆施工设计具有重要意义。由图4可知，浆液在不同流动阶段中高位流动的扩散形态不同，其转变规律如图9所示(红色区域表示高位流动扩散区域，其中，为等效圆半径；′为高位流动扩散距离；为裂隙两侧壁面宽度，m；，，分别为扩散阶段、临界阶段、堆积阶段等效圆心与扩散锋面对应的等效圆心角)。

由图9可知，裂隙倾角为0时，浆液的理想扩散形态为以注浆口为圆心的圆形；而裂隙倾角不为0时，浆液扩散形态在重力影响下发生改变，但高位流动扩散封面始终保持为弧形。在自由扩散阶段(图9(a))，低位流动趋势大于高位流动，该阶段的高位流动扩散锋面为圆弧，圆弧所对应的等效圆心为，则其扩散形态可视为以为圆心的圆弧和弦围成的弓形。浆液进入受限堆积阶段(图9(c))后低位流动消失，浆液的扩散受两侧壁面的限制向上堆积，该阶段的高位流动扩散锋面为圆弧，圆弧所对应的等效圆心为，则其扩散形态可视为以为圆心的圆形与两侧壁面以及与注浆口中心平齐的围成的区域。

在浆液流动阶段的转变中，等效圆的半径受侧壁的影响在过渡阶段内存在临界状态(图9(b))，此时等效圆心与注浆口距离为0，即注浆口()与受限堆积阶段的等效圆心重合，此时等效圆半径与高位流动扩散距离′相等，该临界状态可视为高位流动扩散形态开始受侧壁面间距离影响的最初状态。为此，以临界状态为界将高位流动过程划分为临界状态之前的扩散阶段和临界状态后的堆积阶段。

图9 不同流动阶段高位流动扩散形态转变规律Fig.9 Transition law of high-position flow diffusion form in different flow stages

根据三角形的构成条件，临界状态下满足

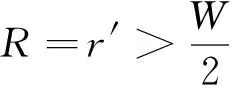
(11)

可将高位流动距离小于侧壁距离一半的高位流动划分为扩散阶段，大于侧壁距离一半的高位流动划分为堆积阶段。基于此定义，在扩散阶段内浆液高位流动扩散面积(m)为

(12)

等效圆心与注浆口距离为

(13)

根据半角公式，有

(14)

联立式(12)～(14)可得

(15)

求解式(15)，取其正根可得

(16)

则高位流动扩散阶段扩散锋面弧长为

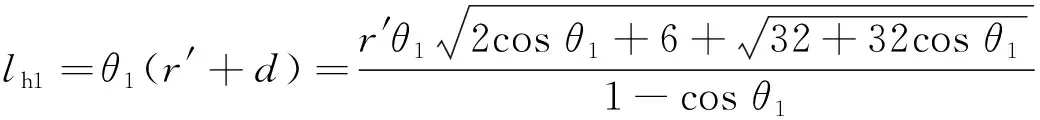
(17)

在高位流动的堆积阶段，浆液受两侧壁面限制，其扩散面积(m)为

(18)

等效圆心与注浆口距离为

(19)

根据半角公式，有

(20)

联立式(18)～(20)可得

(21)

高位流动堆积阶段扩散锋面弧长为

(22)

根据质量守恒定律，任意时间内高位流动的注入量等于该时间内高位扩散覆盖的总体积，即

=

(23)

式中，为高位流动面积，m。

联立式(6)与式(21)，(23)可分别得出高位流动扩散阶段和堆积阶段的流量为

(24)

结合扩散锋面弧长表达式可知，决定高位流量与扩散锋面弧长中的等效圆心角为未知变量，其影响因素与流动状态转变的影响因素有关。为此，针对本文建立的物理模型，选取注浆速率、注浆时间、裂隙倾角作为反演变量，结合数值模型中高位扩散面积计算结果，对式(24)中扩散阶段和堆积阶段的等效圆心角进行反演，反演结果为

(25)

高位扩散阶段、高位堆积阶段的等效圆心角反演相关系数分别为0.984，0.992，说明等效圆心角的变化与注浆速率、裂隙倾角和注浆时间具有良好的相关关系，精度能够满足模型计算需求。由此，联立式(8)，(17)，(25)并进行分离变量积分，代入式(5)可得浆液高位流动扩散阶段注浆压差Δ为

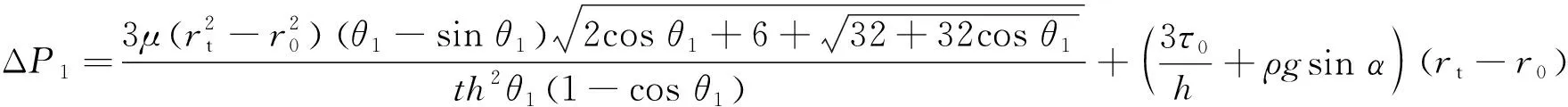
(26)

联立式(8),(22),(25)并进行分离变量积分，代入式(5)可得浆液高位流动堆积阶段注浆压差Δ为

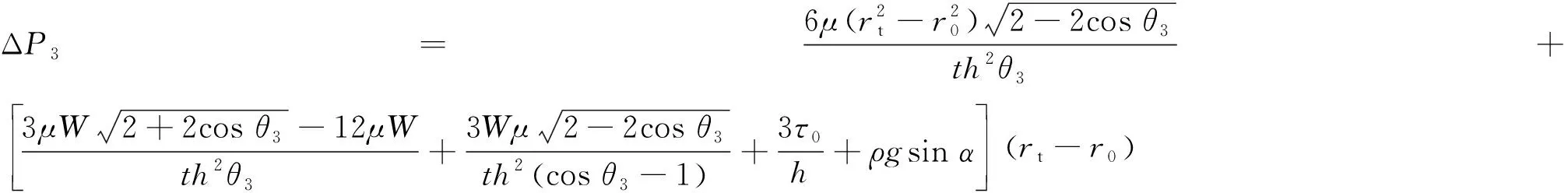
(27)

3.2 模型验证

为验证浆液高位流动扩散阶段和堆积阶段数学模型的有效性，取不同计算工况下375个样本，以注浆压力作为对比指标，将数学模型与数值模型计算结果进行对比。扩散阶段与堆积阶段数值模型与数学模型计算结果相对误差如图10所示。

图10 数值模拟与数学模型相对误差Fig.10 Relative error between numerical simulation and mathematical model

由图10(a)可知，扩散阶段数学模型与数值模型计算结果的最小误差为0.14%，最大误差为25.07%，最小误差出现在注浆速率0.20 m/s、倾角75°计算工况的过渡阶段，最大误差出现在注浆速率0.05 m/s、倾角75°计算工况的自由扩散阶段。注浆速率0.05，0.10，0.20 m/s时，相对误差分别为0.30%～25.07%，0.18 %～19.63%，0.14%～13.28%。注浆速率0.10， 0.2 m/s工况时数学模型与数值模型相对误差在所有流动阶段内均低于20%，而注浆速率0.05 m/s工况仅在自由扩散中期误差超过20%，表明扩散阶段数学模型在工程误差允许范围内具有一定合理性。

由图10(b)可知，堆积阶段数学模型与数值模型计算结果的最小误差为0.071%，出现在注浆速率0.10 m/s、倾角60°计算工况的自由扩散阶段；最大误差为6.62%，出现在注浆速率0.20 m/s、倾角15°计算工况的自由扩散阶段。注浆速率0.05，0.10，0.20 m/s工况内，相对误差分别为0.18%～2.49%，0.071%～2.26%，0.24%～6.62%。堆积阶段所有工况数学模型与数值模型相对误差均低于20%，表明堆积阶段数学模型在工程误差允许范围内具有一定的合理性。

综上，经过与数值模型计算结果对比得出，高位流动数学模型中相对误差低于20%样本占比为97%，相对误差低于10%样本占比为78.4%，误差总体在工程应用允许范围内，表明高位流动数学模型具有一定合理性。

3.3 工程意义

(1)根据高位注浆的扩散形态的转变规律可知，浆液在不同时间段高位裂隙深部扩散范围受裂隙边界影响，仅当底部裂隙空间被填充完毕后，浆液才会在裂隙边界支撑下快速向深部堆积，因此在现场高位注浆设计时应先探明裂隙区域的边界范围。

(2)注浆速率对高位扩散距离的影响程度随流动阶段的演化逐渐增大，且过大的注浆速率会减缓高位流量的损耗并加快流动阶段的转变，因此在实际工程中若仅针对上覆煤岩表层区域范围的裂隙封堵可采用较低的注浆速率，以延长自由扩散阶段的时长，有利于浆液低位流动快速填充底部裂隙空间。

(3)倾角在自由扩散阶段和过渡阶段对注浆压力的影响较小，而注浆速率对初始注浆压力的影响较大，因此在实际工程中，若对煤岩裂隙深部区域进行注浆充填时，可先使用较高的注浆速率，待浆液进入受限堆积阶段后降低注浆速率，使注浆压力控制在安全可控的范围内。

(4)注浆压力在浆液进入受限堆积阶段后将发生突变，因此在实际工程中可通过压力表变化来反映浆液的流动状态，以此推测裂隙的封堵情况。

4 结 论

(1)高位注浆中浆液流动过程可划分为自由扩散阶段、过渡阶段、受限堆积阶段3个阶段。自由扩散阶段，浆液初期扩散形态呈圆形，随着流动时间增加逐渐变为椭圆形；过渡阶段，浆液整体扩散形态逐渐由椭圆形转变为“n”形；受限堆积阶段，整体扩散形态由“n”形转变为类矩形。

(2)浆液进入受限堆积阶段后分流系数达到峰值，此时注浆管注入的浆液体积均为高位流动所增加的体积。不同工况下分流系数变化规律表明，过大的裂隙倾角加大了高位流量的损耗并加快了流动阶段的转变，过大的注浆速率减缓了高位流量的损耗并加快了流动阶段的转变。

(3)裂隙倾角和注浆速率的增加提高了扩散相同距离所需的注浆压力，注浆压力随倾角的增长呈非线性变化，在初期自由扩散阶段注浆压力随裂隙倾角变化不明显，而在高位堆积阶段的增幅产生较大差异。同时，过大的裂隙倾角也加大了裂隙底部区域压力，裂隙倾角越大，底部区域压力值增幅越大。

(4)基于高位流动扩散锋面变化规律，将高位流动划分为扩散阶段与堆积阶段，并通过反演证实等效圆心角与注浆速率、裂隙倾角和注浆时间相关性较好。浆液高位流动数学模型与数值模型的最小误差为0.07%，最大误差为25.08%，且97%样本相对误差在20%以内，78.4%样本相对误差在10%以内，表明高位流动数学模型在工程误差允许范围内具有一定合理性。