旋切作用下岩石破碎机理及岩石可钻性的试验研究
冯上鑫,王善勇
(1. 西安科技大学 建筑与土木工程学院,陕西 西安 710054;澳大利亚纽卡斯尔大学 工程学院,澳大利亚 纽卡斯尔 2308)
地层岩石可钻性评价是岩土钻掘工程中钻头优选、钻速优化以及地层岩体参数识别的重要手段,合理选取岩石可钻性评价指标对控制工程进度和成本具有重要意义。研究表明,岩石可钻性是机岩相互作用的综合表征参数,其大小同时受岩体性质和钻进工艺的影响。但钻进过程中岩石破碎处于封闭空间,钻具响应数据匮乏且离散,导致岩石破碎机理模糊不清,以至于大量岩石可钻性评价指标缺乏理论基础且未被广泛用于实际工程中。如何快速且准确地识别地层岩石可钻性分布,是理论和实践中亟待解决的关键科学问题。
为揭示钻进过程中岩石破碎机理,学者通过大量室内岩石切割破碎试验探明了岩石破碎表象特征规律,并提出相应的岩石破碎模型。其中Merchant切割模型、Evans岩石切割模型以及Nishimatsu岩石切割模型等都对岩石破碎过程中机岩相互作用机制和破碎特征进行定性描述,并广泛应用于提高岩石破碎效率和地层岩体参数预测精度研究。但OUYANG等认为,上述岩石破碎模型只描述了二维岩石切割破碎过程,而岩石切割破碎过程是一个三维复杂破碎过程,为此在上述模型基础上,结合岩石空间膨胀理论,提出了考虑深切割模式下的三维岩石切割破碎模型。另一类岩石切割破碎模型为Detournay和Defourny基于特定力学假定提出的岩石切割破碎现象模型,该模型认为岩石切割破碎主要包括岩石切割和摩擦作用2个过程,通过模型的切割摩擦曲线可快速划分岩石切割过程和量化岩体力学参数。其他类型的岩石破碎模型(如能量耗散分析模型和分形模型)也揭示岩石的破碎机理。
同时部分学者通过钻具响应数据与岩体参数的相关性研究,分析地层岩石可钻性分布。然而由于钻具响应数据随机波动大、辨识度低且数据量巨大,导致建立钻具响应数据与实际地层岩体参数之间的映射关系困难。
尽管在室内试验和现场工程的基础上初步建立了一些经验关系,但由于大多数钻进工程数据有限,建立的岩石可钻性指标适用性一般,难以满足工程普适性。为此,岳中琦等基于时间序列监测技术提出了一种旋转冲击钻自动监测系统,并开展了大量现场钻进试验,发现在同一钻机和钻头下,钻进一块均匀完整的岩块时钻进速度为常数。TEALE等根据钻进功能关系提出了钻进比能参数(钻进单位体积岩石所需要的能量),根据量纲分析认为钻进比能与岩石单轴抗压强度的比值可定量评价岩石的可钻性。在钻进比能的基础上,建立了钻进比能与岩体力学参数的经验公式,以量化岩石可钻性和脆性等参数指标。
但在钻进过程中,钻进压力、旋转速度等随时变化,钻进速度的变化规律受钻进压力和钻头旋转的影响,钻进速度无法保持恒定。同时钻进比能实质为钻机输入机械能,而非钻机的破岩能,若直接建立钻进比能与岩体参数之间的映射关系评价地层可钻性,则忽略了钻进过程中功能转换规律。POLETTO等研究表明,钻进过程中钻机输入机械能以热能、动能、破岩能等不同形式的能量释放,其中只有钻进破岩能作用于岩石破碎,但破岩能在机械输入总能的占比与施加的钻进参数密切相关。因此在钻进过程中,将钻进速度和钻进比能作为岩石可钻性评价指标在一定程度上有待商榷,只有滤除钻进参数的影响,才能建立一个合理岩石可钻性评价指标。
目前岩石可钻性研究缺乏挖掘机岩相互作用过程中岩石破碎本质,导致地层可钻性评价缺乏理论基础;同时大多数的岩石可钻性评价指标未滤除钻进参数的影响进而导致其适用性一般。因此开展钻头旋切作用下岩石破碎机理研究,并在此基础上进行岩石可钻性理论分析是突破岩石可钻性研究瓶颈的关键。
笔者通过室内岩石旋切破碎试验开展机岩相互作用过程中岩石破碎机理研究,明晰机岩相互作用特征及岩石破碎主要影响因素(假设机岩相互作用过程中钻头为刚体,不考虑岩石对钻具影响),确定岩石破碎过程中旋切扭矩变化规律,进而提出不受钻具参数影响且仅与岩体固有属性相关的岩石可钻性理论评价模型,并通过原位钻进数据验证该模型在实际工程中的有效性。
1 室内岩石切割破碎试验
1.1 岩体参数确定
岩石样品取自河南新乡太行山脉采石场,通过X射线衍射仪的岩性分析发现,岩石主要由花岗质片麻岩、方解石大理岩以及白云质灰岩组成,具体岩性分析见表1。
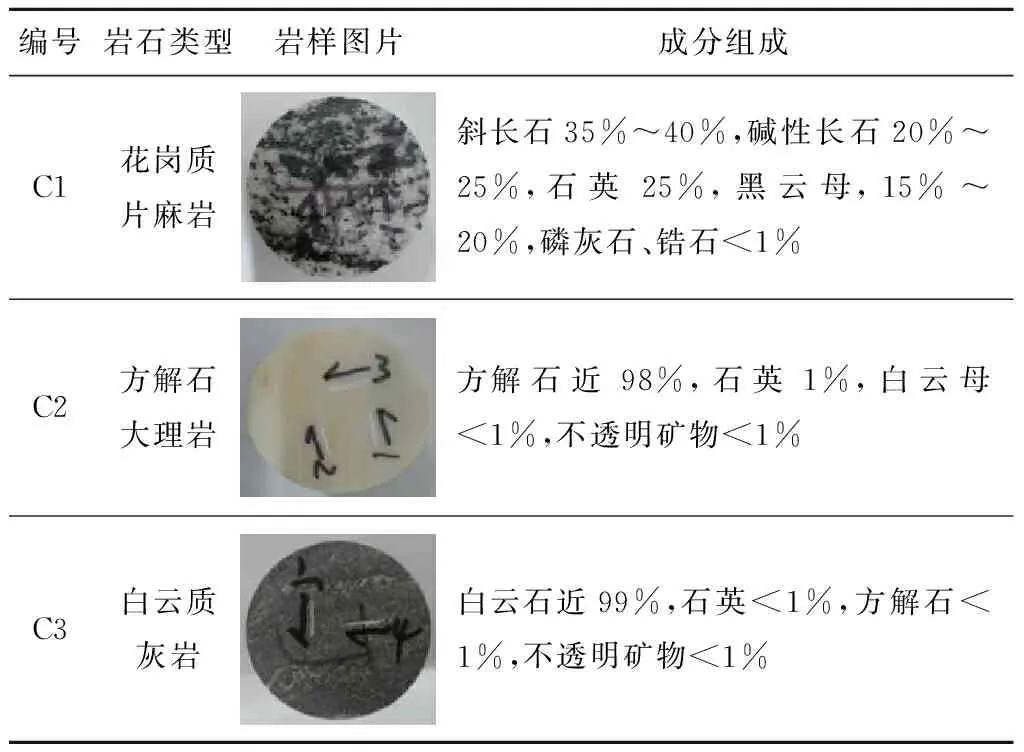
表1 岩石成分分析Table 1 Mineralogical analysis of rock samples
将上述3类岩石制成标准圆柱形岩样(50 mm×100 mm),进行岩石三轴压缩及变形试验和磨蚀试验,以获得岩样的单轴抗压强度、抗拉强度、抗剪强度以及耐磨性指数(ICA)(图1)。其中每种岩样在围压为0,1,2,3,4 MPa下进行三轴压缩及变形试验(每种试验条件进行5次岩石三轴压缩及变形试验),以获得岩石力学强度;同时每种岩样进行5次CAI值测量,即采用5根钢针对同一岩样进行测量,具体

图1 岩石三轴试验及磨蚀试验示意Fig.1 Schematic view of rock triaxial stress and cerchar testing
岩体参数见表2。由表2可知,上述岩石的岩体参数呈一定梯度分布,其中白云质灰岩抗压强度最高,其他岩体参数次之;而花岗质片麻岩抗压强度居中,其他岩体参数都属最高;方解石大理岩各项岩体参数最低。
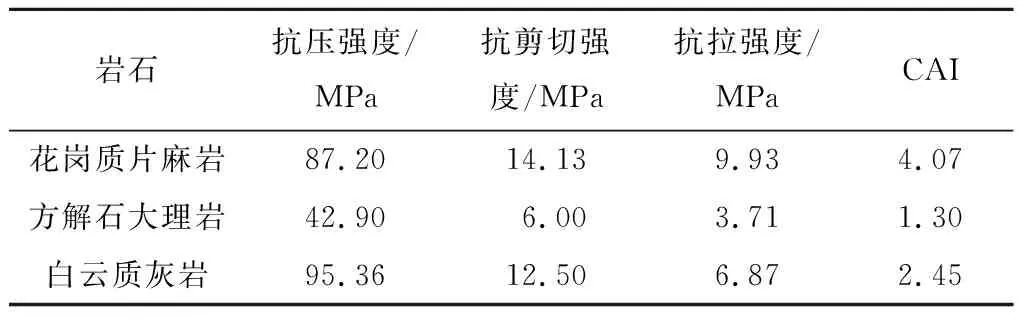
表2 岩石三轴试验及磨蚀试验结果Table 2 Rock triaxial stress and cerchar testing results
1.2 室内岩石切割破碎装置
采用如图2所示的室内岩石旋转切割装置进行岩石旋切破碎试验。该岩石旋转切割装置包括BDS型磁力钻机、承压装置、数据采集系统以及高速摄像机。其中磁力钻机由于体重较轻、吸附能力强且存在过扭和过热保护,适用于室内机械、岩土等钻孔操作,常被选为室内旋切破碎试验仪器。本试验选取BDS-MAB-1300型磁力钻机,该磁力钻机性能稳定、精度高、操作简单,可根据试验要求改变加载压力、旋转速度以及钻头类型。承压装置为自行研制的岩样夹持容器盒,该承压装置可根据岩样尺寸改变夹持口直径,同时可通过改变夹持口螺栓位置调整岩石围压大小。室内传统切割装置多为直接监测钻机施加的扭矩和加载压力,由于扭矩和压力沿钻杆损耗导致岩石实际承受的旋切扭矩和加载压力与钻机施加的扭矩和加载压力有偏差。因此该承压装置将扭矩传感器、压力传感器以及围压传感器都嵌入承压装置中,实时监测岩样实际承受的扭矩、加载压力以及围压大小。数据采集系统用于记录上述传感器的信息并实

图2 岩石旋转切割装置示意Fig.2 Schematic diagram ofrock cutting test apparatus
时显示各传感器随时间变化,同时对采集的传感器数据进行整理以固定格式传送到电脑内,并以EXCEL编排格式显示所有数据,显示格式为:时间-位移-加载压力-扭矩-钻速-围压。在试验过程中,高速摄像机可实时记录不同钻进条件下岩石破碎表象特征。室内岩石旋转切割装置参数见表3。

表3 岩石旋转切割试验装置Table 3 Schematic view of rock cutting test apparatus
1.3 室内切割破碎试验方法
在完成的基本岩石力学试验后,基于岩石旋转切割装置开展不同钻进条件的岩石旋切破碎试验。具体试验步骤如下:在钻头角度为90°,120°,180°,加载压力为0.72,1.33,1.95,2.56 kN,转速为30 r/min的钻进条件下对上述3种岩样进行旋切破碎试验,其中每种岩石在每类钻进条件下进行3次试验。待钻头旋转30 s后停止试验,利用筛分法对岩屑质量和尺寸进行统计以确定破碎颗粒粒径分布,其中筛孔直径包括1.4,1.18,0.85,0.6,0.3,0.212 mm和75,35 μm,如图3所示。最后确定各粒径质量和特征粒径大小,并通过高速摄像机实时记录不同钻进条件下岩石破碎表象特征。

图3 破碎岩屑粒径分布统计Fig.3 Size distribution of fragmentations by sieving method
在钻头角度为180°、旋转速度为30,50 r/min的钻进条件下对上述3种岩样施加不同的加载压力,其中每种岩石在每类钻进条件下至少进行3次试验。通过数据采集系统记录不同加载压力下的旋切扭矩变化,确定岩石破碎过程中加载压力与旋切扭矩的相关关系,探讨机岩相互作用过程中岩石破碎机理,从而进行岩石可钻性理论研究。
2 试验结果与分析
2.1 机岩相互作用过程中岩石破碎机理
在岩石破碎机理研究方面,大部分国内外研究都集中在描述岩石线性切割破碎的表象特征,对岩石持续旋转切割破碎过程描述较少。主要原因是大部分的研究对钻孔岩石切割破碎进行线性切割简化,而实际破岩过程中钻头不仅只有线性切割过程,还包含持续的贯入破碎过程,导致实际岩石切割破碎过程并非线性切割过程,而是钻头与岩石相互作用的复杂过程。
表4为高速摄像机记录的岩石旋切破碎过程。由表4可知岩石破碎过程主要包括贯入压缩破碎阶段和切割破碎阶段。在加载压力作用下钻头开始贯入岩石表面(贯入压缩破碎阶段),随后钻头在旋切扭矩的作用下开始横向切割被贯入的岩石(切割破碎阶段),在岩石切割破碎的同时钻头持续贯入岩石内部,导致钻头在岩石内部运动轨迹呈螺旋线型(持续切割破碎阶段)。在持续切割破碎阶段部分大尺寸的岩屑因吸收了较大切割破碎能而发生崩裂,而大部分岩屑堆积在钻头切割槽内。其中堆积在切割槽内的小尺寸岩屑在钻头切削过程中通过切割路径被拖拽至钻头底部。当钻进深度持续增加,堆积的岩屑不能及时清洗,需要克服的摩擦能急剧增加,导致切割效率下降。

表4 岩石切割破碎阶段Table 4 Rock breakage stages by cutting
为精细化展示岩石破碎过程,结合岩石钻掘理论和岩石破碎试验结果绘制不同视角下岩石破碎情况(图4)和机岩相互作用过程(图5)。岩石在钻头加载压力和旋切扭矩作用下形成应力集中区,当作用力大于岩石单轴抗压强度时,钻头在岩石表面形成岩石贯入压缩破碎区,破碎区的体积、形状与综合作用力大小有关。在岩石贯入破碎区边界存在大量源于贯入破碎区的扩展裂纹(图5(a))。岩石贯入破碎区形成后,旋切扭矩通过破碎的颗粒给岩石传递切削力,在岩石与钻头切向接触位置发生剪切破坏,形成剪切裂纹(图5(b))。在剪切裂纹末端,岩石应力状态低于岩石韧性断裂标准,剪切裂纹分叉成拉伸裂纹。随着拉伸裂纹持续扩展,当裂纹与岩石表面相交时岩石发生破碎(图5(c))。岩石切割破碎后,钻头旋切扭矩会急剧下降,钻头在加载压力作用下再次与岩石接触并循环切割岩石(图5(d)),呈螺旋状侵入岩石(图4)。对比3类岩石的切割破碎情况发现,不同岩性的岩石均遵循上述机岩相互作用过程中岩石破碎机理(表4),主要区别在于抗拉强度、抗剪强度及磨蚀性低的岩石,切割深度大、切割效率高(切割体积大),易出现大尺寸的岩屑。

图4 机岩相互作用螺旋切割轨迹Fig.4 Helicoidal trajectories of the cutter

图5 机岩相互作用过程中岩石破碎Fig.5 Whole process of rock drilling
综上,岩石旋切破碎同时经历压缩破坏、剪切破坏、拉伸破坏以及岩石与钻头附近的韧性断裂破坏。岩石内部裂纹始于贯入压缩破碎区域,其发育程度主要同时受剪切破坏和拉伸破坏影响,而裂纹进一步扩展主要受拉伸破坏控制。
2.2 岩石破碎影响因素
在机械破岩过程中,岩石破碎效率往往是决定工程经济可行性和工程进度安排的重要评价指标。定性分析岩石破碎过程中影响因素是优化机械破岩过程破岩效率和厘清岩石破碎机理的关键。
图6为岩石单轴抗压强度与破碎岩屑质量的关系。由图6可知,岩屑质量随着岩石单轴抗压强度的升高而降低,降低速率随抗压强度升高而持续提高。由岩石破碎机理和CHIAIA等研究可知,当加载压力相同情况下,贯入深度随抗压强度升高而降低,且速率逐步增大,即单轴抗压强度越小的岩石钻头贯入深度越大,钻头每旋转一圈切割破碎的岩屑质量也越大。

图6 岩石单轴抗压强度与岩屑质量的关系Fig.6 Relationship between UCS and the mass of rock chips
图7为岩石抗拉强度与岩屑粒径的关系(为岩屑颗粒累积分布为90%的大尺寸粒径,是评价岩石破碎程度的重要指标)。由图7可知,大尺寸的岩屑随着岩石抗拉强度的升高而降低,降低速率随抗拉强度升高而持续增大。由岩石破碎机理和Evans岩石破碎模型可知,岩石切割破碎过程中,控制岩石破碎程度的一个重要因素为岩石抗拉强度。在相同钻进参数下,钻机输入能量不变,岩石抗拉强度越小,破碎单位体积的岩石所需能量越少,导致破碎岩屑尺寸较大,降低速率也随抗拉强度升高在持续提高。

图7 岩石抗拉强度与岩屑d90的关系Fig.7 Relationship between rock tensile strength and d90 of rock chips
综合图6,7可知,岩石破碎过程中,岩石抗压强度和抗拉强度分别影响岩石旋切破碎过程中的岩屑质量和尺寸分布。
图8,9分别为加载压力与岩屑质量和岩屑粒径的关系。由图8可知,加载压力与破碎岩屑质量呈对数关系(>0.87),随着加载压力增加,破碎岩屑质量也持续增加,但增加速率降低。由图9可知,岩屑粒径与加载压力呈指数关系(>0.52),且增加速率持续增加。由岩石破碎机理和CHIAIA等研究可知,在钻进过程中钻头贯入深度随着加载压力增加呈对数增加,随着加载压力增加,钻进输入能量也持续增加,贯入深度的对数增加导致破碎岩屑质量增加,但增加速率降低。在钻头输入能量持续增加过程中,钻头需要克服的摩擦能比例保持相对稳定,用于形成破碎岩屑的切割破碎能持续增加,同时贯入深度随加载压力呈对数增加,2者共同导致大尺寸岩屑()随加载压力呈指数增加。

图8 加载压力与岩屑质量关系Fig.8 Relationship between loading pressure and the mass of rock chips

图9 加载压力与岩屑d90的关系Fig.9 Relationship between loading pressure and d90 of rock chips
图10为方解石大理岩在不同钻头角度下的岩石破碎情况。由图10可知,在切割破碎过程中,钻头角度越小,岩屑破碎量越大。主要原因是相同切割条件下,钻头角度越小,钻头贯入岩石深度越大,且小角度钻头的破岩方式属于锥体形状渐进分段式破岩,破岩速度高于大角度钻头,导致小角度的钻头具有较高的破岩效率。

图10 不同钻头角度下的岩石破碎情况Fig.10 Relationship between loading pressure and bit angles
3 岩石可钻性分析
3.1 岩石破碎过程中机岩信息互馈研究
在钻进过程中,旋切扭矩不仅是机岩相互作用最直接综合表征参数,也是大量岩石可钻性评价指标的重要中间计算参数。然而在钻孔破岩过程中,实际旋切扭矩大小不仅很难测量,且由于岩石破碎过程中机岩信息互馈机制不明,旋切扭矩也很难通过经验映射关系预估。为提高岩石可钻性评价理论基础,笔者通过室内岩石旋切破碎试验和理论分析开展岩石破碎过程中旋切扭矩变化规律研究。
在岩石破碎过程中,钻头根据运动状态分为正常旋转切割状态和卡钻状态。钻头加载压力较小时,钻头输入的能量大于岩石破碎能和摩擦能,岩石可被正常切割破碎。随着加载压力增加至临界值时(),待破碎岩石的体积较大,钻头输入的能量低于岩石破碎能和摩擦能,钻头处于卡钻状态。其中卡钻临界状态由钻机输入功率大小和岩石性质共同决定。
加载压力小于时,钻头一直处于旋转状态。由Detournay和Defourny研究可知,岩石破碎过程中机岩相互作用可分解为岩石切割和岩石摩擦2个过程。岩石破碎受到的加载压力和扭矩可分解为切割分量和摩擦分量(式(1)、图11)。
=+=+
(1)
式中,,分别为加载压力作用于岩石切割和摩擦分量,N;,分别为岩石旋切扭矩和摩擦扭矩,N·m。

图11 岩石切割破碎模型概念示意Fig.11 Schematic of the rock drilling phenomenological model
由CHIAIA等研究可知,钻进过程中钻头贯入深度和岩石贯入压缩破碎区的半径与钻头形状、加载压力以及岩石类型有关,即
=
(2)
式中,为钻头形态参数,其大小取决于钻头类型和角度等参数;为岩石材料参数,主要受岩石抗压强度影响,根据文献[22],=1。
在岩石破碎过程中,切割单位体积的同种岩石所需的破岩能量是固定的,即岩石固有切割比能。其中切割单位体积的岩石切割力可表示为
d=d
(3)
其中,为切割单位体积的岩石所需能量,J;为岩石切割半径,m。根据极限平衡关系,岩石旋切扭矩可表示为
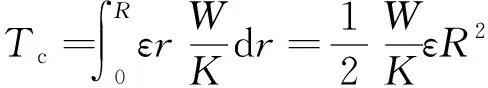
(4)
式中,为钻头半径,m。
由摩擦引起的摩擦扭矩为

(5)
其中,为岩石摩擦因数。由图4可知,钻头是以半径为的2片轴对称压头进行岩石切割破碎,因此岩石切割过程中总扭矩可表示为

(6)
可根据数据采集系统实时监测的扭矩和加载压力快速量化。加载压力大于时,钻头的输入能量低于岩石破碎能和摩擦能导致钻头卡钻。根据极限平衡关系,当钻头处于卡钻临界状态时岩石旋切扭矩为
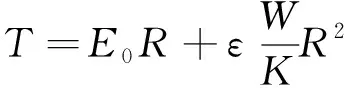
(7)
式中,为卡钻临界状态时钻头受到的最大静摩擦力,N。
图12为根据式(6),(7)绘制的岩石破碎过程中加载压力与旋切扭矩变化规律。由图12和式(6),(7)可知,加载压力与岩石旋切扭矩之间呈正线性关系(黑色实线),且钻头旋转速度不影响岩石旋切扭矩变化。在旋转状态时,岩石摩擦因数和切割比能越高,线性斜率越高(红色实线)。加载压力增至临界压力时,钻头出现卡钻现象,此时岩石切割比能是影响线性斜率的主要因素,岩石切割比能越高,线性斜率越高。

图12 岩石切割过程中加载压力与扭矩变化Fig.12 Relationship between thrust and torque during cutting
图13为3类岩样在不同旋转速度下加载压力与旋切扭矩的关系。

图13 不同岩石在切割破碎过程中的扭矩变化Fig.13 Torque variations of different rocks during cutting tests
由图13可知,岩石破碎过程中,加载压力与旋切扭矩的关系呈如图12所示的线性关系,且3类岩石破碎过程中仅有花岗质片麻岩石出现旋转状态和卡钻状态。钻头处于旋转状态时,3种岩性的旋切扭矩呈线性变化且斜率变化规律也如图12所示,其中抗拉、抗剪强度以及磨蚀系数最高的花岗片麻岩的旋切扭矩变化斜率最高,而抗拉、抗剪强度及磨蚀系数最低的方解石大理岩的旋切扭矩变化斜率最低。同时旋转速度不影响岩石旋切扭矩变化,主要原因是钻头旋转速度只能改变岩石切割速率,不能改变瞬时岩石切割体积。同时由式(6),(7)可知,旋切扭矩只与岩石固有性质及瞬时岩石切割体积相关,与钻头旋转速度无关。根据文献[25]的原位钻孔试验数据也发现,钻孔岩性保持恒定时,钻进加载压力和旋切扭矩的确呈正线性关系,且钻头旋转速度不影响该线性关系。
3.2 岩石可钻性理论评价模型
图14为岩石切割破碎过程,结合岩石破碎机理和机岩信息互馈研究,假设钻头钻进一圈过程中钻头压力不变,由式(6)可知,旋转状态下钻头扭矩不变。

图14 钻进过程中钻头运动简图Fig.14 Simplified diagram of bit movement during cutting
在钻头每旋转一圈的钻进深度为时,切割破碎一圈岩石的扭矩可表示为

(8)
式中,为质元张角(图14)。
根据钻孔几何关系和式(8),切割破碎一圈岩扭矩为

(9)
用于克服摩擦过程的摩擦扭矩可表示为
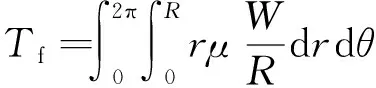
(10)
由钻孔几何关系,式(10)可表示为
=π
(11)
由式(9),(11)可得总钻进扭矩为

(12)
将式(6)代入式(12)可得

(13)

(14)
由式(13)可知,钻进过程中加载压力与单钻钻进深度的线性斜率主要受岩石固有切割比能和摩擦因数影响,与钻进过程中加载压力和旋转速度无关。同时根据文献[25]原位钻孔试验数据发现,钻孔岩性保持恒定时,加载压力与钻头每旋转一圈的钻进深度呈正线性关系,且不同旋转速度下的加载压力与单钻钻进深度的线性梯度保持恒定,相关系数大于0.61,如图15所示。在实际工程中,将加载压力与单钻钻进深度的线性关系梯度作为岩石可钻性评价指标。且在实际钻掘工程中,钻进监测系统可实时记录钻进过程数据,随后通过岩石可钻性评价模型计算地层岩石可钻性沿钻孔深度分布。

图15 钻进过程中加载压力与单钻钻进深度的关系[25]Fig.15 Relationship between thrust and penetration per revolution[25]
4 结 论
(1)在岩石破碎过程中,钻头在贯入和切割共同作用下呈螺旋线型侵入岩石内部并导致岩石分别发生贯入破碎、剪切破碎和拉伸破碎。其中部分大尺寸岩屑因吸收的破碎能较大而发生崩裂,但大部分破碎岩屑堆积在钻头切割路径内且增加了切割摩擦能。
(2)钻头加载压力是岩石破碎程度的重要影响因素。在相同加载压力下,破碎岩屑质量和尺寸分布分别受岩石抗压强度和抗拉强度影响。
(3)在岩石破碎过程中,岩石旋切扭矩与加载压力成正线性关系,且岩石摩擦因数和岩石切割比能越高,该线性斜率越大;钻头旋转速度不影响岩石旋切扭矩变化。
(4)在岩石破碎过程中,钻头单钻钻进深度和加载压力的线性斜率只与岩石固有切割比能和岩石摩擦因数相关,在一定钻进条件下不受钻进过程中钻具参数变化的影响,可作为地层岩石可钻性评价的参考指标。

