基于避难场所容量限制的地震应急疏散路径分析

魏本勇 董翔 谭庆全 齐文华 郭欣欣

摘要：针对地震灾害应急疏散策略，构建了一种基于避难场所容量限制的灾民应急疏散分配与路径选择算法模型。该模型综合考虑了避难场所的容量受限性和人口分布的不均匀性，在兼顾避难场所容量限制的同时，使灾民的总疏散距离成本最小化。以北京市东西城为例，对给定情景下的灾民应急疏散路径进行了实证研究。研究发现，在考虑避难容量限制的情形下，无论是地震初期，还是地震中后期，研究区域内现有应急避难场所的容量都不足以满足区域居民的避难需求。基于实际道路疏散成本和避难容量限制的灾区应急疏散路径评估模型，不仅能够给出各疏散需求点最佳的疏散目的地和具体路径，还能给出避难容量限制下各需求点疏散到不同目的地的人数，以及无法满足避难需求的居民数量。

关键词：避难场所;应急疏散;路径分析;地震灾害;北京市

中图分类号：P315.953 文献标识码：A 文章编号：1000-0666（2022）01-0141-09doi：10.20015/j.cnki.ISSN1000-0666.2022.0015

0 引言

避难疏散是减轻自然灾害影响与损失的重要措施，也是自然灾害应急响应的重要组成部分（Ikeda，Nagasaka，2011）。面对自然灾害或突发公共安全事件冲击时，科学合理地实施应急疏散策略，可以有效地提高灾时社会的避难疏散效率和应急响应能力，最大限度地减轻人员伤亡，保障救灾工作的顺利实施与社会稳定。然而，在突发灾害或安全事件下，如何快速合理地选择最佳疏散路径和安全空间是一个巨大的挑战。由于恐慌、混乱、缺乏疏散知识或日常演练等原因，灾区的部分居民往往无法及时找到最佳疏散路径或安全的疏散目的地。

目前，在应急避难疏散方面，国内外学者已进行了诸多的相关研究。如美国早在20世纪70年代即针对三里岛核电站事故开发了应急疏散模型（Cova，Church，1997;Cova，Johnson，2001），该模型通过评估疏散的可用时间和避难场所的可达性判定疏散时间，从而确定所用时间最短的疏散路线。Cova等（2005）使用“疏散触发点”的概念评估了易受火灾影响的社区中的风险人群以及疏散所需的时间。Simonovic和Ahmad（2005）给出基于计算机的洪水应急疏散计划模型。Chen等（2005）提出了一种估计飓风中人员撤离和疏散时间的方法。Dulebenets等（2019）提出一个混合整数规划模型，将个人（包括弱势群体）在可用时间段内通过疏散路线分配到应急避难场所，考虑了疏散人员的社会人口特征、疏散路线特征、驾驶条件和交通特征对疏散人员出行时间的影响。在避难场地适宜性与选择方面，Pine 等（2003）基于飓风灾害，综合评估了飓风避难场所的功效;Gall（2004）在莫桑比克实施了一个避难场所选址的适宜性模型;Kongsomsaksakul等（2005）提出了一个针对洪水疏散计划的避难场所位置分配模型，适宜性的评估标准包括易受伤害人口的位置、靠近道路、当地基础设施和农田;Kar和Hodgson（2008）通过构建一种避难场所适宜性方法，对佛罗里达州的应急疏散避难场所进行了评估和排序。

国内在城市应急避难场所效能分析、区位选择及空间布局等领域也取得了一定研究进展（苏幼坡，刘瑞兴，2004;陈志芬等，2010;徐立鹏等，2012;袁昀等，2015;魏本勇等，2019）。王海鹰（2005）以福建福清市为例，研究了城市地震应急避难场所的选择及疏散道路选择问题;黄静等（2011）以上海市陆家嘴街道为研究对象，从应急疏散需求分布、疏散空间可达性、疏散优化归属3方面逐步构建了居民避震疏散区划方法;Liu等（2011）基于汶川地震案例，提出了山区应急避难场所选择的方法;Hu等（2014）提出了一种解决地震避难地点和分区规划问题的数学模型;施益军（2015）研究了云南山地小城市应急避难场所的空间布局和优化问题;周爱华等（2016）利用GIS两步移动搜寻法对北京城区应急避难场所的可达性进行了分析;Chen和Cheng（2020）通过分析西安市城镇复杂环境下的地震疏散行为发现，虽然大部分居民都会选择安全的疏散目的地，但都不是离他们居所最近的目的地，且居民的疏散行为具有显著的组间差异。然而，由于避难场所的空间有限，加之避难场所基本都具有“平、灾”两用的性质，其位置与人口避难需求分布可能并不完全匹配（魏本勇等，2019）。这就可能会引起灾时应急疏散人员分配的不均衡性，从而导致发生疏散滞后甚至无法疏散的状况。因此，科学合理地分配应急避难场所对于保证应急疏散安置效率具有重要的意义。

大地震灾害通常会引起巨大的恐慌。尤其在地震灾害初期，受灾群众对灾害及次生灾害情况还不清楚，防备能力不足，通常会全部进入避难场所进行避难。如果缺少科学合理的避难疏散规划，那么从居民点到周边避难场所疏散的无序性必然会增加疏散安置过程的混乱与无效（Li et al，2008）。因而，加强对地震应急疏散规划的研究，对于提升震后应急疏散效率，稳定灾后社会情绪都具有重要的现实意义。科学合理地对避难场所进行分配，除了需要考虑疏散时间最短之外，还必须考虑每个避难场所的容量和所需疏散居民的空间分布，以使得应急疏散过程中每个所需疏散空间单元被指定到尽可能近的避难场所。据此，本文综合已有前期研究基础和应急避难需求，提出了地震應急避难疏散路径选择的基本原则：①灾区民众（疏散点）到其分配的避难场所的距离总和尽可能最小;②每个避难场所分配的疏散人口总数不能超出其已知最大设计容量;③为保证就近疏散，尽可能使每个避难场所分配的疏散点具有空间连续性。依据上述基本原则，基于ArcGIS平台，本文构建了一种考虑容量限制和疏散时间最短的地震应急疏散模型，以北京市东西城为例，对给定地震情景下的灾民应急疏散路径进行了实证分析。

1 震后灾民应急疏散模型构建

1.1 疏散安置网络数据集构建

网络数据集构建是网络分析的基础和前提。一个基本的网络主要由点状要素和线状要素及其属性组成。以往关于地震灾区应急疏散最佳路径的选择，通常以欧式距离作为主要评估参数，其结果对于强调实际道路网络分析的应急疏散研究的适用性较差。本文选择实际道路网络作为测算疏散需求点与目的地之间距离成本的基础参数。

应急避难场所以点要素的形式表达，以其实际中心点作为目的地的位置。疏散需求点也以点要素的形式表达。道路以线要素的形式表达，作为连接各应急避难场所及避难人员疏散的通道。将研究区域道路网络数据进行拓扑，创建道路网络数据集，并生成网络分析图层。因此，地震应急疏散空间几何网络即是包含疏散需求点（i，如格网点、居民点等空间单元）、道路（节点）网络（f）、应急避难场所（j）的矢量数据集。其中I（i∈I）为疏散需求点集、J（j∈J）为目的地点集、F（f∈F）为网络节点U（u∈U）间的路段数据集。

1.2 地震应急疏散模型算法

1.2.1 最短疏散路径成本评估模型

疏散时间/距离成本最小，是选择地震应急疏散路径的首要条件之一，也是空间可达性研究的主要内容。本文以疏散距离最小化为目标，基于解决最短路径问题的Dijkstra算法计算疏散需求点i与疏散目的地点j的距离矩阵D（dij∈D），可得其评估公式为：

D=∑dij=∑min（fiu， fuj） （i=1，2，…，n;j=1，2，…，m）（1）

式中：dij表示疏散需求点i至避难场所j的最短网络距离;fiu表示疏散需求点i与节点u的路段长度;fuj表示节点u至避难场所j的路段长度。

疏散需求点i归属避难场所j（疏散目的地）的判断条件如下：

∑ni=1aij=m（2）

aij= 0 （dij>Rmax） 1 （dij≤Rmax）（3）

式中：aij表示疏散需求点i与避难场所j的归属关系;当aij=0时，表示疏散需求点i无法归属于避难场所j;当aij=1时，表示疏散需求点i归属于避难场所j;Rmax表示避难场所的最大服务半径。

1.2.2 考虑避难场所容量约束下的最短疏散路径评估模型

基于空间可达性的疏散需求点归属分析，只保证了居民在有限的时间/距离内能够到达避难场所，但不能避免可能出现部分场所超出容量限制，而部分场所又出现极为空闲的不合理现象。因此，在分析避难场所空间可达性的基础上，还应考虑避难场所的实际容纳能力。为此，在参考黄静等（2011）研究基础上，基于最短疏散路径成本分析，本文建立了以容量限制与避难归属唯一为约束条件，以避难场所服务覆盖人数最大化为目标的灾民应急疏散评估模型。其具体评估方法如下：

Cj=max∑mj=1∑ni=1aijPi（4）

Cj≤TCj（5）

aij=0，dij>d（i+1）j1，dij≤d（i+1）j（6）

∑ni=1aij≤m（7）

式中：Cj表示避难场所j所覆盖的疏散需求人数;Pi表示疏散需求点i的人口数;TCj=St/S0表示避难场所j的人口容量，St为避难场所的有效面积，S0为人均有效避难面积;aij表示需求点i与避难场所j的归属关系。

2 模型算法开发

该模型算法是基于ArcGIS10.6版本系统下的Python2.7开发的扩展工具系统，其开发流程主要包括路网数据准备、系统数据预处理、最优疏散路径计算和疏散路径输出与展示4个部分。具体算法实现过程如图1所示。首先，利用路网创建预处理工具处理道路数据，修正道路路网的联通性，指定要计算的路径成本类型（时间、距离等），并将预处理后的路网数据生成网络数据集备用。其次，进行评估数据预处理，准备疏散需求点（如居民点位置和灾民数量）和疏散目的点（如避难场所位置和容量）数据，如路网有中断，则需要指定相应的阻抗点（道路中断的位置）。然后，利用上文确定的地震应急疏散模型，计算所有需求点到所有目的点的通达成本，获得整体的origin-destination（OD）成本矩阵结果;校验成本矩阵，将不可达的两点补充虚拟值，将结果求解转为线性规划问题;再计算分配矩阵，利用线性规划算法，计算需求点和目的点的最佳分配方式。最后，根据最佳生成结果，计算需求点和目的点的实际疏散路径，并输出展示实际疏散路径及其属性（如疏散成本、疏散人数等）。

3 实证研究

3.1 研究区概况

北京市是我国大陆东部多地震的地区之一。历史上曾发生过多次强烈地震，如1679年三河—平谷8.0级、1057年大兴6.8级和1730年颐和园6.5级等重大地震灾害。虽然北京市一直十分重视城市综合防灾减灾相关建设工作，但由于北京市人口密集、建筑密度大且高层建筑多，因此一旦遭遇重大灾害或突发公共安全事件，实施应急避难及救援的任务更重，对应急疏散安置与避难场所需求更高。魏本勇等（2019）的研究也表明，虽然北京市应急避难场所总体分布与人口分布趋势基本一致，但其总体设计容量远低于需求容量，且区域间差异明显。

北京市东西城位于中心地区，是首都功能核心区，共包含32个街道办事处，地区总面积约为92.54 km2。2019年东西城的常住人口为193.1万人，平均常住人口密度高达20 866人/km2，远高于北京市整体平均人口密度（1 312人/km2）。根据统计，截至2016年12月，北京市东西城统计在案的地震应急避难场所只有13个，包括Ⅰ类应急避难场所1个、Ⅱ类4个、Ⅲ类8个，总面积仅为68.26万m2，属于应急避难场所服务配置需求缺口较大的地区（魏本勇等，2019）。因而，其未来面对应急疏散安置与避难需求的任务更艰巨。基于此，本文以北京东西城为例，以公里格网尺度的空间单元作为人口疏散需求點，以区域地震应急避难场所为疏散目的点，应用本文开发的地震应急疏散模型评估系统，对给定情景下的区域人员应急疏散路径进行了实证案例分析，以期为未来区域应急疏散与救援避难策略的制定提供参考。

3.2 数据资料与处理

在地震初期，群众对灾害及次生灾害情况不清楚，防备能力不足，尤其当地震发生在夜晚、高人口密度的地区时，更容易引起恐慌性疏散，因而设定研究区地震应急疏散的需求为全部区域人口数量，即区域人口疏散需求的上限。在地震灾害中后期，地震及其次生灾害影响一般已得到控制。此时，住房未被破坏的居民将陆续返回家中，只有住房破坏严重的灾民需要继续在避难场所避难，因此，疏散安置人员需求应视当地房屋抗震能力等因素确定。根据对北京市房屋建筑抗震防灾工作调查http：//zjw.beijing.gov.cn/bjjs/xxgk/xwfb/318135/index.，北京市1976年后新改建房屋已基本满足Ⅷ度设防要求，只有旧城平房区及个别简易楼抗震能力不足，综合北京市各方面情况，拟按地震烈度Ⅷ度时15%的房屋及设施损毁率，即约30%的居民需要进入避难场所进行避难安置测算。

本文以公里格网尺度的人口分布空间单元，作为地震情景下的疏散需求点。人口数据为2010年全国第六次人口普查调查数据。疏散目的地为截至2016年12月统计在案的北京市地震应急避难场所，包括各避难场所的名称、位置、有效面积等基本信息，此数据由北京市地震局提供（表1）。由于避难场所一般都有多个不同的进出口，到达目的地点（不同进出口位置）的不同，也会对具体疏散路径和成本产生一定的影响。但由于数据限制，本文以各应急避难场所的中心点位置作为疏散目的地点。路网数据为矢量化的城市道路网，包括道路名称、宽度、长度等基本属性信息，由北京市地震局提供（表1）。结合国内外及前期研究，本文人均有效避难面积采用2 m2核算（魏本勇等，2019）;由于只考虑步行疏散，因而疏散路径成本以距离成本衡量，考虑实际疏散现实和居民平均步行速度，本文限定疏散距离成本为2 km范围内，即居民疏散的最远目的地为距离疏散需求点2 km。

通过构建北京东西城地震应急疏散网络数据集（疏散需求点和目的地均为点状数据集;道路网络为线状数据集），基于开发的地震应急疏散模型评估系统，即可给出给定情景下的北京东西城地震应急疏散最佳路径与策略。

3.3 北京东西城地震应急疏散路径分析

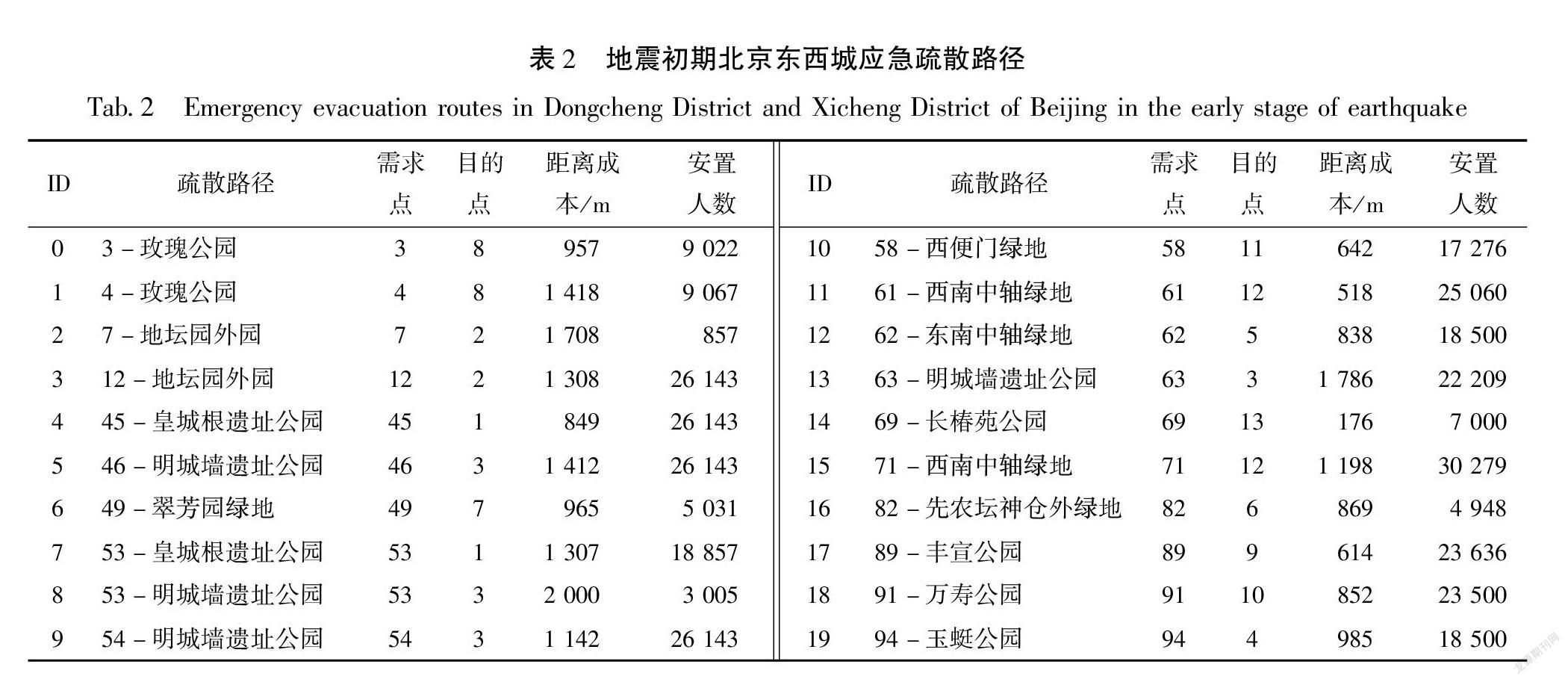
图2展示了在地震发生初期情景下，北京市东西城的民众应急疏散与安置路径。由图可见，在考虑全体居民疏散情形下，以区域内现有应急避难场所为疏散安置点，其疏散分配缺口为1 739 860，说明有超过170万人因为避难场所的容量限制而得不到安置，区域内现有应急避难场所的容量不能满足实际疏散需求。表2給出了各疏散需求点（格网单元）具体的疏散路径和疏散目的地（应急避难场所），以及各避难场所对应能够安置的不同需求点的居民数量。从表2中可以看出，在考虑全体居民需要应急疏散安置的情形下，由于疏散需求巨大，各避难场所的容量最大仅能满足其周边2 km范围内的居民疏散需求，区域内避难容量远不能满足周边居民的避难疏散需求。

图3展示了地震灾害发生中后期，只考虑住房破坏严重的灾民需要继续避难的情景。虽然地震中后期，各疏散需求点需要继续避难安置的人口数较地震初期有了较大幅度的下降，但评估结果发现，北京市东西城现有应急避难场所仍不能满足区域内居民的疏散需求。即使在不考虑疏散距离（2 km）限制情景下，当地居民应急疏散分配缺口仍达到283 055。在这种情况下，虽然部分避难场所的服务空间可以扩展到最远6.5 km的区域，但仅目前区域内的避难空间容量仍不能满足避难需求，仍有超过28万人因为避难场所的容量限制而得不到疏散安置（图3）。而如果考虑疏散距离（2 km）的限制，则当地将有近40万（39.46万）的居民因避难场所容量限制而无法疏散安置（表3）。因而，无论是在地震初期还是中后期，北京东西城现有的应急避难场所容量无法满足实际避难需求。在制定当地的应急疏散策略与疏散路径时，除了需要考虑实际道路疏散成本外，更重要的还要考虑应急避难场所的容量限制。只有兼顾避难场所容量限制与实际道路疏散成本的灾民应急疏散路径评估，对于制定科学合理的应急疏散策略才有更实际的参考意义。

4 结论

本文基于ArcGIS平台，开发了一种考虑容量限制和疏散距离成本最短的地震应急疏散评估模型，并以北京市东西城为例，对给定情景下的灾民应急疏散路径进行了实证研究，得到如下主要结论：应急疏散路径的选择需要兼顾疏散成本和避难场所容量。对北京市东西城居民应急疏散的实例分析发现，无论是考虑地震初期，还是地震中后期，区域内现有应急避难场所的容量都不足以安置所有需要疏散的人口。基于实际道路疏散成本和避难容量限制的灾区应急疏散路径的评估模型，不仅能够给出各疏散需求点最佳的疏散目的地和具体路径，还能给出避难容量限制下各需求点疏散到不同目的地的人数，以及无法满足避难需求的居民数量。这不仅能为区域灾民应急疏散策略选择提供科学依据，也能为未来的区域避难场所规划建设提供参考基础。

本文实际案例研究中，只考虑了研究区域内的避难场所分布。实际上，在应急疏散中，区域外的避难场所也同样可以参与分配。本文最主要目的是构建一种能够兼顾避难场所容量且疏散成本最低的地震灾害应急疏散路径评估模型，因而未将研究区外的避难场所纳入评估。另外，本文设定避难场所中心点位置为疏散目的地到达点，这在一定程度上会影响避难场所的实际服务范围与疏散路径规划，尤其是对于超大面积且多出入口的避难场所。未来，随着数据的完善，可以进一步提升地震应急疏散评估模型结果的准确性和实用性。

参考文献：

陈志芬，顾林生，陈晋，等.2010.城市应急避难场所层次布局研究（I）——层次性分析[J].自然灾害学报，19（3）：151-155.

黄静，叶明武，王军，等.2011.基于GIS的社区居民避震疏散区划方法及应用研究[J].地理科学，31（2）：204-210.

施益军.2015.山地小城市应急避难场所的空间布局优化研究——以云南剑川为例[D].昆明：云南大学.

苏幼坡，刘瑞兴.2004.城市地震避难所的规划原则与要点[J].灾害学，19（1）：87-91.

王海鹰.2005.城市地震应急避难场地、道路选择合理性初探——以福清市为例[D].北京：中国地震局地质研究所.

魏本勇，谭庆全，李晓丽.2019.北京市应急避难场所的空间布局与服务效能评估[J].地震研究，42（2）：295-303.

徐礼鹏，刘启蒙，孙娇娇.2012.基于GIS的安庆市应急避难场所空间布局特征分析与优化[J].测绘与空间地理信息，35（2）：151-155.

袁昀，刘杨，朱思洪，等.2015.应急避难场所选址最大准备度覆盖模型及其算法[J].自然灾害学报，24（2）：8-14.

周爱华，张景秋，张远索，等.2016.GIS下的北京城区应急避难场所空间布局与可达性[J].测绘通报，（1）：111-114.

Chen C，Cheng L .2020.Evaluation of seismic evacuation behavior in complex urban environments based on GIS：a case study of Xi an，China[J].International Journal of Disaster Risk Reduction，43（5）：101366.

Chen X，Meaker J W，Zhan F B.2005.Agent based modelling and analysis of hurricane evacuation procedures for the Florida Keys[J].Natural Hazards，38（3）：321-338.

Cova T J，Church R L .1997.Modelling community evacuation vulnerability using GIS[J].International Journal of Geographical Information Science，11（8）：763-784.

Cova T J，Dennison P E，Kim T H， et al.2005.Setting wildfire evacuation trigger points using fire spread modeling and GIS[J].Transactions in GIS，9（4）：603-617.

Cova T J，Johnson J P.2001.Microsimulation of neighborhood evacuations in the urban wildland interface[J].Environment and Planning A，34（12）：2211-2229.

Dulebenets M A，Pasha J，Abioye O F， et al.2019.Exact and heuristic solution algorithms for efficient emergency evacuation in areas with vulnerable populations[J].International Journal of Disaster Risk Reduction，39：101114.

Gall M.2004.Where to go Strategic modelling of access to emergency shelters in Mozambique[J].Disasters，28（1）：82-97.

Hu F Y，Yang S N，Xu W.2014.A non-dominated sorting genetic algorithm for the location and districting planning of earthquake shelters[J].International Journal of Geographical Information Science，28（7）：1482-1501.

Ikeda S，Nagasaka T.2011.An emergent framework of disaster risk governance towards innovating coping capability for reducing disaster risks in local communities[J].International Journal of Disaster Risk Science，2（2）：1-9.

Kar B，Hodgson M.2008.A GIS-based model to determine site suitability of emergency evacuation shelters[J].Transactions in GIS，12（2）：227-248.

Kongsomsaksakul S，Yang C，Chen A.2005.Shelter location-allocation model for flood evacuation planning[J].Journal of the Eastern Asia Society for Transportation Studies，6（1）：4237-4252.

Li X，Claramunt C，Kung H T， et al.2008.A decentralized and continuity-based algorithm for delineating capacitated shelters  service areas[J].Environment and Planning B：Planning and Design，35（4）：593-608.

Liu Q，Ruan X J，Shi P L.2011.Selection of emergency shelter sites for seismic disasters in mountainous regions：lessons from the 2008 Wenchuan MS8.0 Earthquake，China[J].Journal of Asian Earth Sciences，40（4）：926-934.

Pine J C，Marx B D，Levitan M L， et al.2003.Comprehensive assessment of hurricane shelters：Lessons from Hurricane Georges[J].Natural Hazards Review，4（4）：197-205.

Simonovic S P，Ahmad S.2005.Computer-based model for flood evacuation emergency planning[J].Natural Hazards，34（1）：25-51.

Analysis of the Earthquake Emergency Evacuation Route Basedon the Capacity of Shelters

WEI Benyong1，2，DONG Xiang3，TAN Qingquan4，QI Wenhua1，2，GUO Xinxin1，2

（1.Key Laboratory of Seismic and Volcanic Hazards，China Earthquake Administration，Beijing 100029，China）

（2.Institute of Geology，China Earthquake Administration，Beijing 100029，China）

（3.Shandong Earthquake Agency，Jinan 250014，Shandong，China）（4.Beijing Earthquake Agency，Beijing 100080，China）

Abstract

Evacuation is an important measure to reduce the impacts and losses from natural disasters.Scientific and timely selection of the best evacuation path is of great significance for improving the efficiency of emergency evacuation and for the stability of society after an earthquake.For the measure of the earthquake emergency evacuation，an algorithm model of emergency evacuation arrangement and path selection based on the capacity of shelters is constructed.The model minimizes the cost of total evacuation distance for victims by considering the capacity of shelters and the uneven distribution of the population.Taking Dongcheng District and Xicheng District of Beijing as samples，the selection of the emergency evacuation route for the victims in a given scenario is studied.It is found that the capacity of the existing emergency shelters is not enough to meet the need of the residents living in the area，whether in the early stage or in the late period of an earthquake event.The evaluation model of emergency evacuation route in the disaster area based on the evacuation cost of the actual route for victims and the shelters  capacity，can not only give the best evacuation destinations and specific routes for each place on demand for evacuation，but also provide the number of the victims on demand for evacuation to different destinations as well as the number of the victims remained unevacuated.

Keywords：emergency shelters;emergency evacuation;path analysis;earthquake disaster;Beijing City