基于GIS和专家知识的滇西南地区滑坡敏感性模糊逻辑推理方法

白仙富 戴雨芡 叶燎原 聂高众 徐硕 罗伟东 于江 徐昕

摘要：为了充分识别和有效减轻滑坡灾害风险，对滇西南南涧（约470 km2）和凤庆—昌宁（约2 300 km2）两个研究区开展了基于GIS和专家知识的滑坡敏感性模糊逻辑评价研究。通过检查模型计算得到的历史滑坡点敏感性值与整个研究区域的滑坡敏感性平均值是否不同来评价本方法的性能，用Z值检查来测试差异的统计显著性。计算结果显示，南涧地区的Z值为4.1，相应的P值小于0.001，表明通过模型计算得到的滑坡敏感性值是该区域滑坡事件发生的良好指标;凤庆—昌宁地区的Z值为8.93，相应的P值小于0.001。在此基础上，采用自然断点法对滑坡敏感性值进行分类，根据分类结果将滑坡敏感性水平划分成5个等级：极低（0.0～0.001）、较低（0.001～0.051）、中等（0.051～0.394）、较高（0.394～0.557）和极高（0.557～1.0）。敏感性极低和较低的地区没有发现历史滑坡记录;敏感性极高地区的历史滑坡密度约是敏感性较高地区的4倍，约为敏感性中等地区的10倍。凤庆—昌宁地区的研究结果表明，从区域专家群中提取的滑坡敏感性与环境因子关系的知识可以外延到滇西南其它地区。

关键词：滑坡敏感性;专家知识;模糊逻辑;约束算术平均法;滇西南地区

中图分类号：P315.942 文献标识码：A 文章编号：1000-0666（2022）01-0118-14doi：10.20015/j.cnki.ISSN1000-0666.2022.0013

0 引言

滑坡是山区最常见的地质灾害之一，它不仅对自然生态系统和人类基础设施有重大破坏，还会造成大量人员伤亡和财产损失（Chung et al，1995;Dai，Lee，2002;Lee，Choi，2004;Guzzetti et al，2005）。为了减少滑坡灾害损失和减轻滑坡灾害风险，很多地区都开展了大量识别滑坡易发地点的敏感性研究（Carrara，1988;Carrara et al，1991;van Westen et al，1993;Aleotti，Chowdhury，1999;Alexander，2008;Carrara，Pike，2008），并建立了许多滑坡敏感性评估模型。受印度洋板块持续向北东方向推挤、青藏高原地块强烈隆起的影响，云南地区地势从西北向南东方向逐级降低，加之河流侵蚀等外营力的影响，境内许多地区山高坡陡，滑坡现象普遍。对云南地区滑坡风险的研究一直是该区域地质灾害研究的一个重要内容。随着GIS理论与技术的兴起，云南滑坡风险研究在县（区）尺度（胡金等，2007，2008;孙黎丽等，2007;杜玉龙，方维萱，2009;钱晶，王瑞斌，2009;周松林等，2010;纪甲子等，2010;吕勇等，2010;田志萌等，2011;颜春达等，2011）、州（市）尺度（刘丽，王士革，1995;丁星妤等，2011;周松林等，2010;于丰泽，武蕾，2012;尹诗琪等，2008;张超等，2016;翟倩倩等，2016）、流域尺度（唐川，2004;谢洪等，2007;李英等，2009）和省域尺度（唐川等，1994;李志斌，郑成德，2000;陶云等，2009;万石云等，2013）等不同地域系统尺度的滑坡特征、滑坡环境因子、滑坡敏感性评价和区划、滑坡治理探索等方面都取得了长足发展。

现有的大多数滑坡敏感性研究在建模时，通常用统计分析方法回归得到历史滑坡和滑坡点位置环境因子的关系。在训练过程中，有滑坡的样本数据质量总体比较可靠（van Westen et al，1993;Carrara et al，1991），而那些没有滑坡的样本数据质量就值得商榷。但这种建模方法存在两方面问题：一是不能很好地识别暂时稳定的滑坡危险区。研究发现滑坡灾害事件总是发生在那些没有重点监视的区域，即在早期的风险隐患底数调查中疏漏并最终影响到了减轻风险的有效实施的区域;二是大范围的滑坡敏感性区划容易忽略高危型区域的“安全岛”和低风险区的高隐患点，对指导具体地域减轻风险的可操作性不足。为了避开或减少以往研究方法固有缺陷的影响，本文提出一种基于GIS和专家知识的滑坡敏感性模糊逻辑评估方法。

朱阿興等（2006）对三峡地区的研究表明，专家知识用于区域滑坡敏感性评价通常能取得令人满意的效果。由于滑坡的发生因地而异，不同研究区内影响滑坡发生的因素也大相径庭，三峡地区与滇西南地区地理环境存在极大差异，因此不适宜直接将三峡地区的模型应用到滇西南地区。另外，对三峡地区滑坡敏感性研究采用的一些方法需要改进，如仅通过一个专家提取滑坡知识、直接使用算术平均法来计算滑坡敏感性综合值等进行滑坡敏感性水平分区。为了改进或部分改进这些研究方法存在的不足，我们建立了新的方法，它与以往评价模型主要有两个方面的不同：一是区域滑坡敏感性知识不是仅仅来自一位专家而是来自一个专家群，二是计算评估位置的滑坡敏感性综合值时，不是直接使用算术平均法计算各环境因子的滑坡敏感性隶属度指数，而是采用一种约束算术平均法来进行空间位置的滑坡敏感性综合值推断。最后，为了检验本文所提出的方法在更广范围地区的外延适用性，用本方法在凤庆—昌宁地区开展滑坡敏感性评价和合理性检验。

1 研究方法

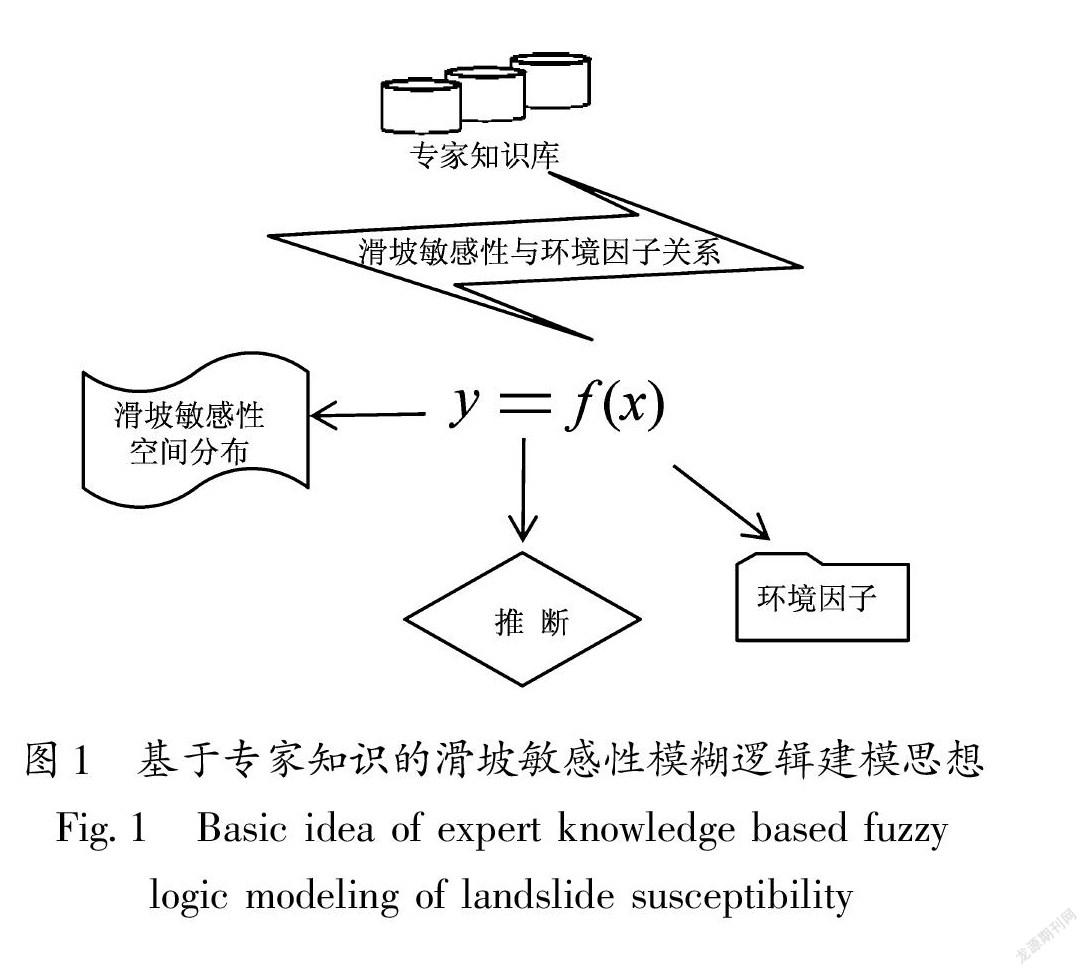
专家知识法是人们通过对物理过程的综合理论理解和根据多年专业领域的职业经验发展起来的一种方法（Luger，2005）。基于专家知识的滑坡敏感性建模方法的基本思想是从当地滑坡专家群里直接提取研究区滑坡敏感性与环境因子之间的关系，然后将这些关系应用于研究区各个位置的滑坡敏感性评价（图1）。这种思路与通用的统计方法进行区域地表滑坡敏感性空间分布评价有明显差别。专家知识法是根据区域专家群的知识对滑坡敏感性和环境因子关系f进行近似处理，而统计方法则是根据历史滑坡事件对关系f进行统计学上的近似处理。在专家知识滑坡敏感性研究方法中，我们利用模糊逻辑提取滑坡敏感性与环境因子之间复杂的非线性关系的专家知识，并将其表示为一组模糊隶属函数。各模糊隶属函数用来描述滑坡敏感性与该环境因子之间的关系。在评价时，利用GIS对研究区的滑坡敏感性环境因子进行网格式地理编码，建立滑坡环境因子栅格空间数据库（Lan et al，2004;Fourniadis et al，2007;Remondo，Oguchi，2009），将专家知识转化为模糊隶属函数与GIS数据库相结合的方式，对研究区各位置的滑坡敏感性进行推断。

在地理建模中，专家知识模糊逻辑模型化或贝叶斯概率建模后，专家知识法的功能就比数据驱动模型所使用的统计功能更可靠、更一致、也具有更好的普适性（Fisher，1989;Hudson，1992;Zhu et al，2004）。在滑坡相关研究领域，专家通过对滑坡敏感性与环境因子之间复杂关系信息的积累形成自己的经验性知识。基于专家知识的滑坡敏感性空间分布推断方法包括3个主要步骤（图2）：①从专家群里提取当地滑坡敏感性与环境因子的专家知识;②利用GIS对环境因子进行特征描述，建立区域滑坡环境因子空间栅格数据库;③根据专家知识进行区域滑坡敏感性空间分布的模糊推断。

1.1 专家知识提取

专家知识的质量和充分性对基于專家知识的滑坡敏感性空间分布模糊建模能否成功至关重要。本文共选取9名当地地质灾害领域专家作为知识提取的对象，模型中不同环境因子的参数值采用专家给出值的调和平均数。我们从区域滑坡专家群里获取两类知识：①在选定的研究空间范围内，确定影响滑坡敏感性的环境因子;②这些环境因子是如何影响滑坡敏感性的，即环境因子与滑坡敏感性之间的关系。

1.1.1 环境因子体系

专家们给出的滑坡敏感性环境因子体系对研究区的滑坡敏感性水平十分重要。区域专家的知识质量影响变量的具体内容和该变量的可外推程度。在滑坡敏感性分析中，常用的环境因子包括地形地貌（坡度、坡向、坡形、相对起伏、平面曲率和坡面曲率等地形变量）、地质构造（岩性、地层倾向和倾角等地质变量）（Oguchi，1997）、土地利用/土地覆被（土地利用类型、植被类型、植被归一化指数等地表变量）、降水（多年平均降水量、短时最大降水量等气象变量）等（Brabb，1984;Atkinson，Massari，1998;Aleotti，Chowdhury，1999;Dai，Lee，2002;Donati，Turrini，2002;Zhu et al，2004;Ermini et al，2005）。本文主要关注气象条件激发的自然滑坡，人类活动、地震动参数等因子诱发的滑坡不在本文研究的考虑范畴内。

1.1.2 模糊逻辑函数建立

对于连续类型数据，在模糊逻辑领域中，函数通常表示为模糊隶属度函数。我们用一个特定的函数来描述滑坡敏感性如何随一个环境因子的变化而变化。模糊隶属度函数有3种主要曲线形式：S形曲线、Z型曲线和钟形曲线（Burrough，1989;MacMillan et al，2000;Shi，2002）。其中，常为大家熟悉的是S形曲线（图3a），这种曲线形式用于环境因子存在有一个阈值的情况，在这个阈值上滑坡敏感性值达到最大，滑坡敏感性随环境因子值的增大逐渐增大，当环境因子值大于该阈值时，基于环境因子的滑坡敏感性保持在最大值。Z型曲线（图3b）是S型曲线的镜像形式，表示本底因子在某个临界值或某个范围内时滑坡的敏感性最高，在临界值时滑坡的敏感性达到最大，而大于该临界值时滑坡的存在敏感性

会减小。钟形曲线（图3c）用于环境因子存在有一个最佳值或一系列最佳值的情况，在此最佳值或在此最佳值范围内，基于环境因子的滑坡敏感性达到最大值;当环境因子值偏离该最佳值或该最佳值范围时，基于环境因子的滑坡敏感性降低。

将滑坡敏感性和各环境因子之间的关系描述为函数f，建模时根据环境因子的有效性和重要性对f进行相应调整。根据环境因子的数据类型，f可以有不同的选择：

fx（dij，x）=P1，x （fdij，v=c1，x）

P2，x （fdij，v=c2，x）

Pm，x （fdij，v=cm，x）（1）

式中：fx为描述滑坡敏感性与环境因子x（类别型）关系的函数，将函数计算得到的值作为滑坡敏感性值，最大为1，最小为0，敏感性值越大滑坡发生可能性越大;dij，x为位置（i，j）处环境因子x的值;P1，x，P2，x，…，Pm，x为因子x取c1，x，c2，x，…，cm，x时对应的滑坡敏感性值。在这种变量类型中，专家在提取知识时可以对每一种或一组环境因子类型对滑坡的影响进行从0到1的相对排序。

通用的高斯型函数比其它函数更容易控制曲线的形状，使拟合的曲线尽可能逼近实际曲线的基本形状，因此本文用高斯函数来表达函数f：

fx（dij，x）=exp-（0.8362dij，x-dxD）2（2）

式中：fx和dij，x与公式（1）定义相同;dx是影响因子x作用下隶属函数值达到最大阈值时x的值;D是控制曲线形状的参数，定义为隶属度为1和0.5时环境因子值之差。曲线类型和参数根据当地专家知识来确定。若专家指出滑坡敏感性随多年平均降水量的增加而增加，则采用S形曲线。如果专家认为，降水量大于1 500 mm（阈值 = 1 500）的地区，滑坡敏感性很高，当降水量降到1 250 mm 时（D=250），滑坡敏感性大约降低一半，就使用其它隶属函数来计算降水环境因子作用下的滑坡敏感性隶属度值：

fP（dij，P）=1（dij，P>1 500 mm）exp-（0.8362dij，P-1 500250）2（dij，P≤1 500 mm）（3）

式中dij，P为位置（i，j）的多年平均降水量。

1.2 研究区基础数据处理

基础数据处理主要是进行研究区地理编码和环境因子栅格数据集开发。为了空间分析的方便，我们将研究区划分为30 m×30 m的网格单元，对这些单元进行地理编码，使得每个网格单元具有坐标位置（i，j）。在ArcGIS中将环境因子都处理为一套30 m×30 m的空间数据集，每一个像元具有对应的地理编码。其中，大部分环境因子可以直接使用ArcGIS的功能菜单实现，比如坡度、地形起伏度、岩性（根据地质图进行矢量处理后转为栅格数据）、降水等，部分环境因子通过二次开发进行特征提取，比如坡形环境因子中的上凸坡、下凹坡等。

1.3 滑坡敏感性模糊逻辑推理

利用模糊逻辑推理技术，把从专家群中提取的研究区滑坡敏感性与环境因子关系同环境因子特征数据相结合，计算每个像元（根据地理编码）位置（i，j）的滑坡敏感性模糊隶属度来获取整个研究区的滑坡敏感性综合值，最后进行滑坡敏感性评价。研究区滑坡敏感性模糊逻辑推理过程如图4所示，首先从滑坡敏感性环境因子数据集中获取该单元的所有敏感因子值，图中有3个环境因子，c1，x、c2，x和c3，x像元中的值分别为 1、2和3;然后，根据专家知识库中环境因子与滑坡敏感性关系计算各环境因子值对应的滑坡敏感性模糊隶属度。图中，以环境因子c1，x、c2，x和c3，x为基础的滑坡敏感性模糊隶属度分别表示为d1ij、d2ij和d3ij。最后，基于这些单个环境因子将滑坡敏感性隶属度值聚集起来，计算像元的总体滑坡敏感性综合值dij。

像元滑坡敏感性值的推理过程可以用一个通用聚合函数公式来表示：

Sij=Tnx=1[fx（dij，x）]（4）

式中：Sij是像元（i，j）的滑坡敏感性;n是滑坡敏感性环境因子个数;T是计算像元（i，j）整体滑坡敏感性指数的聚合函数，对于聚合函数T可以有不同的选择。

采用滑坡敏感性研究中常用的算术平均聚合函数（Liu et al，2004;Zhu et al，2004）计算像元敏感性综合值，容易导致一些区域的敏感值过高。以坡形环境因子为例，平坦型坡形位置上，即使其它环境因子下的模糊函数隶属度值很高也不会有滑坡危险，但在做简单的聚合函数计算时可能就会得到很高的敏感性综合值。因此我们采用约束算术平均聚合函数（式5）对评估位置滑坡敏感性综合值进行计算。所谓约束，就是将独立环境因子作用下滑坡隶属度值为0的条件作为约束，将评估位置上该条件下的滑坡敏感性综合值约束为0，以约束算术平均聚合函数推断出整个区域的滑坡敏感性综合值。最后再基于这个模糊的滑坡敏感综合值，进行整个区域的滑坡的敏感性水平分级，即将滑坡敏感性水平划分为极低、较低、中等、较高、极高5个等级。

Sij=0， fx（dij，x）=0

1n∑n1fx（dij，x），fx（dij，x）>0（5）

式中：Sij是像元（i，j）的综合滑坡敏感性，n是滑坡敏感性环境因子个数;fx（dij，x）为位置（i，j）处环境因子x作用下的滑坡敏感性模糊逻辑模型计算值。

2 案例研究

2.1 研究区域

本文以云南省的南涧和凤慶—昌宁地区为研究区，这2个研究区位于云南西南部，是滑坡多发区，对其进行深入研究有助于掌握风险隐患底数的国情普查和风险减轻理论的深化。南涧地区用来进行滑坡敏感性评价方法的开发和测试，凤庆—昌宁地区位于南涧研究区以西15 km以外，用于检验所开发的滑坡敏感性评估方法外延的适用性。

2.1.1 南涧地区

南涧地处云南省西部横断山系纵谷区，位于云岭余脉的无量山、哀牢山结合部。地势由中南部向东北、西南逐步降低。研究区面积约为470 km2，海拔1 160～2 830 m，平均海拔2 042 m（图5）。地形为高中山地区，除河谷流经区有少量冲积平地外，大部分为河谷、山峦和坡地构成的山区或半山区。研究区主要为南涧县东南部的石洞寺深谷、西南部的公郎河谷及中部与西部大片山岭地区。地貌构成主要有侵蚀构造地貌、侵蚀堆积地貌、剥蚀地貌、断块山地貌、岩溶地貌等。这个地区大部分的斜坡比较陡峭，最高坡度约为51°，平均坡度约为19°。区内地层主要有以下几种类型：坝注路组、花开左组、麦初箐组、三合洞组、景星组、漾江组、外麦地岩组。

2.1.2 凤庆—昌宁地区

凤庆—昌宁地区是凤庆县和昌宁县之间的一个矩形区域，位于南涧研究区西偏南位置，该地区长约66 km、宽约35 km（图6）。研究区地处滇西纵谷南部，以云岭山系和怒山山系为主，地貌依其成因，可划分为构造侵蚀地貌、构造剥蚀地貌和侵蚀堆积地貌3大类型。区内地貌在侵蚀、构造剥蚀、冲积等地质内外应力作用下，中山、低中山、丘陵、盆地、河谷槽坝相间分布，波状起伏，地形地貌条件复杂。这个地区大部分的斜坡比较陡峭，最高坡度约53°，平均坡度约为18°。

凤庆—昌宁研究区地层主要有以下几种类型：景星组、崇山岩群、坝注路组、花开左组、麦初箐组、梅家山岩群、平掌组、学习谦岩群、温泉组、三合洞组、挖鲁八组、向阳寺组、南新组、何元寨组与大寨门组并层、河湾街组、香山组、南林组、栗柴坝组、第四系全新统、漾江组、歪古村组、忙怀组、芒棒组、勐腊组、弯甸坝组、大名山组、施甸组、蒲缥组并层、鱼塘寨组、南梳坝组、丁家寨组与卧牛寺组并层、丙麻组与保山一带的沙子坡组（大凹子）未分或并层、老尖山组、仁和桥组、勐戛组、柳湾组未分、丁家寨组、丙麻组与保山一带的沙子坡组（大凹子）未分或并层、石佛洞组、马平组、老第三纪花岗斑岩、晚白垩世黑云母花岗岩、三叠纪花岗闪长岩、老第三纪白云母、二云母花岗岩、侏罗纪花岗闪长岩、三叠纪—二叠纪二长花岗岩。凤庆—昌宁地区地貌和地质背景与南涧地区相似。从专家中提取的知识表明，该研究区具有与南涧地区相似的滑坡机制，这两个研究区的滑坡敏感性与环境因子之间的关系是相似的。

2.2 南涧地区模型建立与评价

本文方法在南涧地区的建模包括3个步骤：提取专家知识、环境因子层栅格数据集地理表征和滑坡敏感性模糊推理。

2.2.1 专家知识提取

通过从当地专家群提取的滑坡敏感性与环境因子关系知识，确定了7个基本的环境因子：坡度、相对高差、坡形、地质构造、岩性、降水和土地利用类型。其中坡度的影响是最为主要的，属于根本性环境因子，其它环境因子都是基于坡度发生作用的。地质构造对滑坡敏感性有重要影响，相似地形因子因地质构造不同而对滑坡敏感性的影响表现出较大差异。相对高差定义为斜坡山脊的最高点和山谷最低点之间的海拔差，它能够表征整个斜坡的形状而不是某个像元的局部曲率。

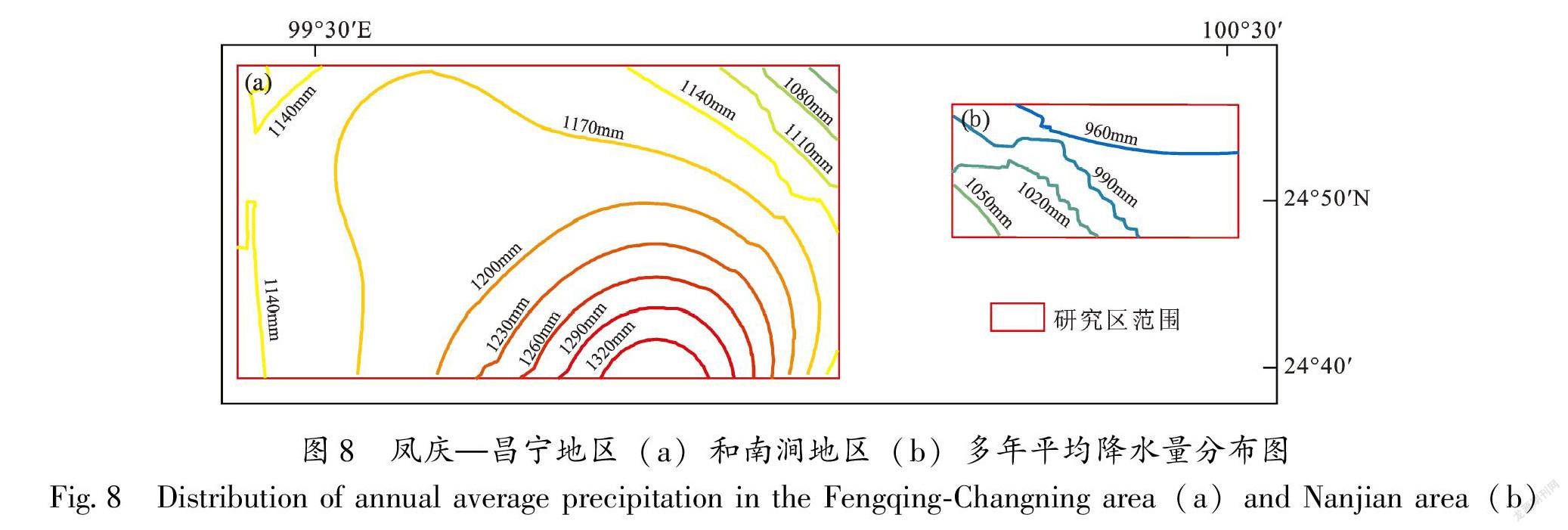
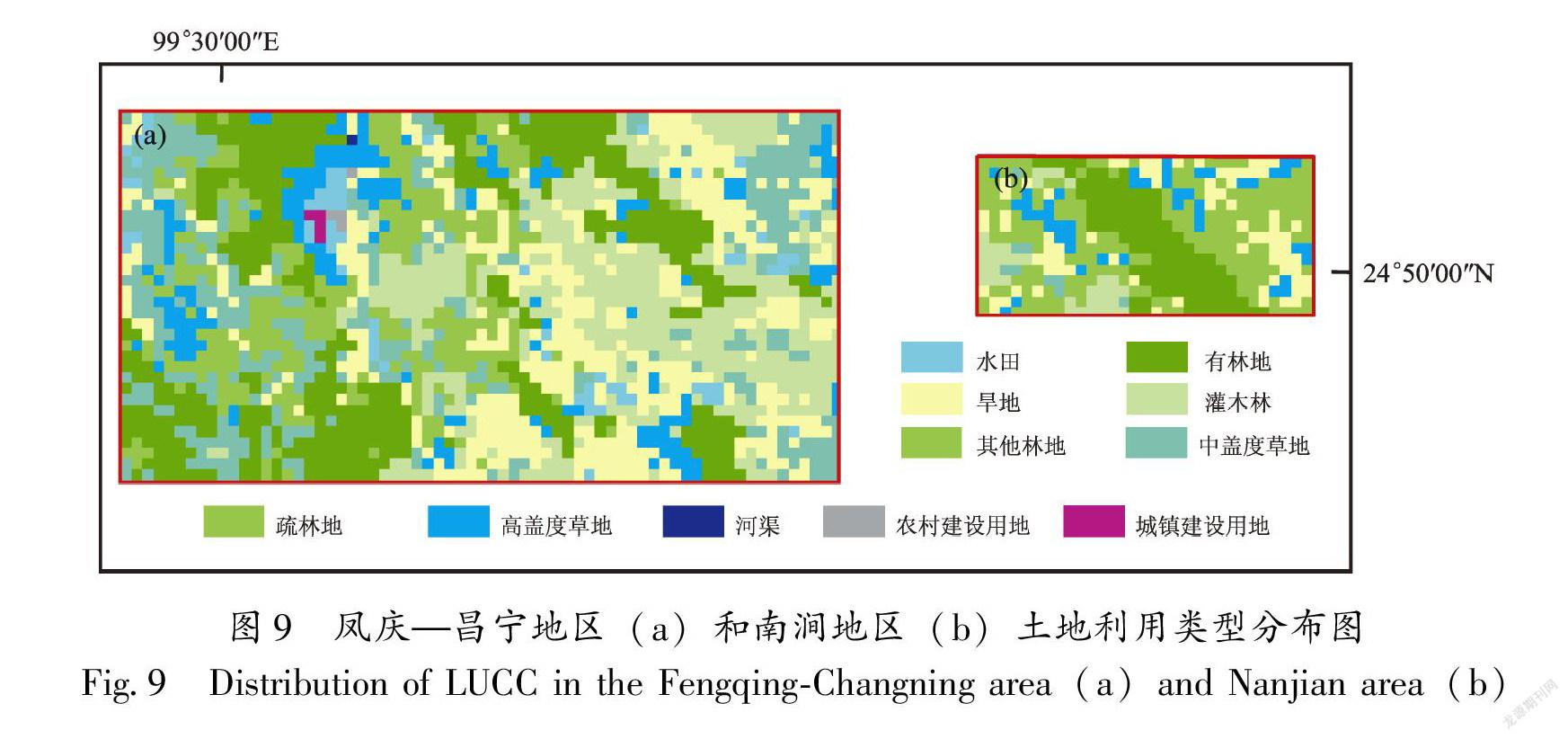
根据专家知识，将研究区斜坡形状划分为6种基本类型（图7）：直型、凹型、凸型、上凸下凹型、上凹下凸型和平缓型。将研究区岩性划分为4种基本类型：类型Ⅰ为坚硬的侵入岩岩组、坚硬的喷出岩岩组、坚硬的石英岩岩组、水体;类型Ⅱ为坚硬的片麻岩、混合岩、变粒岩岩组、坚硬的砂岩、砾岩岩组、坚硬的石灰岩、白云岩岩组、坚硬的大理岩岩组;类型Ⅲ为较坚硬的片岩岩组、较坚硬软弱的砂砾岩夹黏土岩岩组、较坚硬、软弱的砂砾岩、黏土岩互层岩组、较坚硬、软弱的黏土岩夹砂砾岩岩组、坚硬-软弱的碎屑岩夹碳酸盐岩岩组、坚硬、较坚硬的碳酸盐岩夹碎屑岩岩组、坚硬、较坚硬的碳酸盐岩、碎屑岩互层岩组;类型Ⅳ为较坚硬、软弱的千枚岩、板岩岩组、软弱的粘土岩岩组、土体。两个研究区为我国南方湿润地区，境内多年平均降水量都没有大幅度差异（图8），土地利用类型主要有11类，根据它们对滑坡敏感性贡献大小从小到大依次为河渠、高盖度草地、有林地、中盖度草地、其它林地、灌木林、疏林地、旱地、水田、城镇用地和农村建设用地（图9）。当地的专家根据1.1.2节所述的方法，将这些滑坡环境因子表述为模糊隶属函数，我们提取这些知识后综合得到了研究区滑坡敏感性与环境因子之间的关系（表1）。

利用从专家群里提取的知识和具体参数，建立定量描述滑坡敏感性与环境因子之间关系的隶属度函数。

（1）由坡度引起的滑坡敏感性表示为：

fS（dij，S）=1.0（dij，S≥30）

exp-dij，S-30×0.8326202（dij，S<30）（6）

式中：dij，S为位置（i，j）的坡度。

（2）由斜坡类型引起的滑坡敏感性表示为：

fSS（dij，SS）=0.0（dij，SS=6）0.1（dij，SS=3）0.3（dij，SS=5）0.5（dij，SS=1）0.8（dij，SS=2）0.1（dij，SS=4）（7）

式中：dij，SS为位置（i，j）的斜坡形态类型。

（3）相对高差和滑坡敏感性之间的关系与斜坡类型相关，并通过斜坡类型发生作用。不同斜坡类型下由相对高差引起的滑坡敏感性定義为：

fRR（dij，RR）=fSS（dij，SS）×1.0（dij，RR≥400）exp-dij，RR-400×0.83262002（dij，RR<400）（8）

式中：dij，RR为位置（i，j）的相对高差，单位为m。

（4）由岩性引起的滑坡敏感性表示为：

fL（dij，L）=

1.0（dij，L=Ⅳ）

0.5（dij，L=Ⅲ）

0.2（dij，L=Ⅱ）

0.1（dij，L=Ⅰ）（9）

式中：dij，L为位置（i，j）的岩性类型。

（5）地点的构造条件对滑坡敏感性的影响通常与斜坡的坡度和坡向有关， 由构造和斜坡信息组合引起的滑坡敏感性定义为：

fSG（dij，SG）=0 （dij，ag-dij，as>90）

0（dij，d>dij，S）

exp-dij，d-dij，S×0.8326452×cos（dij，ag-dij，as）（dij，ag-dij，as≤90）且（dij，d≤dij，S）（10）

式中：dij，d是位置（i，j）的地层倾角;dij，ag是位置（i，j）的地层倾向;dij，S是位置（i，j）的斜坡坡度;dij，as是位置（i，j）的斜坡坡向。

（6）由多年平均降水量引起的滑坡敏感性定义见公式（3）。

（7）由土地利用类型引起的滑坡敏感性定义为：

fLU（dij，LU）=1（dij，LU≥9）exp-0.8362dij，LU-962（dij，LU<9）（11）

式中：dij，LU为位置（i，j）的土地利用类型赋值。

在得到以上7个环境因子组合之后，我们就可以将每个组合所计算出的模糊函数隶属度值采用约束算术平均法来计算滑坡敏感性综合值。在计算过程中，给各组合的权重是一样的（朱阿兴等，2004），其原因是我们认为约束后每种组合出现的机率大致类似。由于每个组合计算的滑坡敏感性值为0～1（含0和1），因此，通过约束算术平均法得到的综合模糊滑坡危险性也为0～1（包括0和1）。

2.2.2 环境因子栅格图层数据表征

研究区滑坡的环境因子及其数据来源见表2。由于环境因子栅格数据集中，相对高差信息和6类斜坡形态信息的提取难以直接通过ArcGIS软件直接完成，所以需要分步骤来对这些信息进行GIS表征。对地形信息的计算主要分为3个步骤：①提取研究区山脊和山谷信息。山脊和山谷信息可以通过自动化的方式或手工数字化的方式完成，本文使用GIS中的网络提取技术。②计算相对高差。具体算法为从山脊的每个像元（假设海拔高度为H1）沿水流流向向下追踪，直到到达山谷区像元（假设海拔高度为H2）。两者的高程差（即H1-H2）设置为沿此路径（从山脊到山谷）上所有像元的相对高差（单位：m）。③相对高差插值。因为不能保证在上一步计算完成后，研究区内的每个像元都有相对高差值，因此采用邻近插值方法，确保每个像元都有整个区域的相对高差。

斜坡形状信息的提取分为3个子步骤：①提取研究区山脊和山谷信息。②确定斜坡形态类型。从山脊区的每个像元开始，沿着水流流向向下追踪，直到到达山谷区的一个像元为止。记录沿此路径的所有高程值并生成剖面形态，根据坡度形状分类确定沿此路径的斜坡形态类型（图7）。将得到的斜坡形态类型设置为沿此路径（从山脊到山谷）上所有像元的斜坡形态类型。③对整个研究区进行斜坡形态信息插值。采用近邻插值方法对上一步骤后未采集到斜坡形态信息的像元进行斜坡类型信息计算。

2.2.3 滑坡敏感性模糊推理

结合专家知识和滑坡环境因子对南涧地区滑坡敏感性进行模糊推理，推断出的滑坡敏感性如图10所示，可以划分为4个区：①高值和高值相连类型区。连片的高值区域在国土规划整治中应列入不宜开发区，也是滑坡隐患重点监视区。②低值和低值相连区。低值连片区在国土规划整治中可以考虑合理开发利用，为滑坡隐患安全区。上述两类区域是所有类型中占比最大的区域。③低值围绕高值区。这类型地区就是安全区内的高滑坡风险隐患点，对隐患点要特别关注。④高值包围低值区。大多数情况下，这类型区域中的低值区是没有安全意义的，因为高值区发生的滑坡可能对低值区形成影响，因此低值区实际上可能也是潜在滑坡影响区，但是当被包围的低值区面积较大足以缓冲滑坡影响时，则可以成为滑坡隐患区中的安全岛，国土规划整治中要分类考虑。

2.2.4 滑坡敏感性推断的评价

为了评价模型的有效性，需要对模型结果进行检验。在检验方法中，Z值（Z-score）是衡量一组数据中的每一个数据与整组数据的平均值之间的偏离程度，即以标准差为单位表示一个具体数据到平均数的距离或离差。某个点的滑坡敏感性值等于平均值时Z=0，大于平均值时Z>0，小于平均值時Z<0。某个点的滑坡敏感性值越高表示滑坡的可能性越大，那些发生过滑坡或滑坡隐患点位置上的Z值越高越符合该位置容易滑坡的判断。P值（P-Value）也是常用于衡量可信程度的一个递减指标，P值越大，我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。在许多研究领域，根据显著性检验方法所得到的P值，通常认为P值为0.05是可接受错误的边界水平，一般以P<0.05为有统计学差异，P<0.01 为有显著统计学差异，P<0.001为有极其显著的统计学差异。其含义是样本间的差异由抽样误差所致的概率分别小于0.05、0.01、0.001。

本文通过检查模型计算得到的历史滑坡点敏感性值与整个研究区的滑坡敏感性平均值是否不同来评价本方法的性能，用Z值来测试差异的统计显著性。因为研究区DEM是根据1978年制作的地形图创建的，因此对收集到的1978—2000年的65次历史滑数据进行整理和定位，计算得到南涧地区历史滑坡点敏感性Z值为4.1，相应的P值远远小于0.001。这表明计算出的滑坡敏感性值是滑坡发生的良好指标。

通过将滑坡敏感性与其分级相结合，来进一步评价南涧地区滑坡敏感性推断的有效性。采用自然断点法对滑坡敏感性综合值进行分级，根据分级结果将滑坡敏感性划分成5个等级：极低（0.0～0.001）、较低（0.001～0.051）、中等（0.051～0.394）、较高（0.394～0.557）和极高（0.557～1.0）。对滑坡敏感性分级的目的是观察不同滑坡敏感性等级的滑坡密度差异，来进一步评价基于GIS和专家知识的滑坡敏感性模糊逻辑推断效果。从表3可以看到一个明显的趋势，滑坡敏感性水平的增加与研究时段内有记录的野外滑坡事件密度增加有关。滑坡敏感性等级为极低和较低的地区没有发现历史滑坡记录，滑坡敏感性等级为中等地区滑坡密度非常低，其滑坡密度约为敏感性等级为较高区域的1/4，为敏感性等级为极高区域的1/10。

2.3 模型在凤庆—昌宁地区的应用

将南涧地区滑坡敏感性与环境因素之间关系的知识移植到该研究区时，所有指标、参数都不变。凤庆—昌宁地区的滑坡敏感性如图11所示，总体看，本区域内滑坡敏感性分布也有4类，即高值和高值相连类型区、低值和低值相连类型区、低值围绕高值类型区和高值包围低值类型区。我们用同样的方法在凤庆—昌宁地区检测滑坡敏感性推断的有用性。该区共观测到290处滑坡（图11），计算得出的Z值为8.93，相应的P值远小于0.001。这表明计算得出的滑坡敏感性值是滑坡发生的良好指标，我们可以将南涧地区的专家知识外推到滇西南的另一个研究区，并且所建立的方法可以应用于滇西南更大范围的研究区域。

同样通过将滑坡敏感性与滑坡敏感性分级相结合，来进一步评价凤庆—昌宁地区滑坡敏感性推断的有效性。与已建立模型的南涧地区进行对比发现，本研究区也具有相似的滑坡密度差异，同样在滑坡敏感性极低和较低区域没有观察到滑坡，滑坡敏感性较高地区历史滑坡密度约是中等地区的4倍，敏感性极高地区约是中等地区的10倍。这一结果表明，计算得到的滑坡敏感性值可用于预测某地区未来发生滑坡的可能性。

3 讨论

基于GIS和专家知识的滇西南地区滑坡敏感性模糊逻辑方法研究是为了克服当前云南地区滑坡敏感性研究成果中存在的部分缺陷和改进部分现有研究方法的不足，以充分识别区域固有的滑坡风险隐患和可能存在的安全岛。

专家对当地滑坡敏感性与环境因素关系的认识是长期理论研究和实践的结果，总体上认知较一致。所以，模型建立过程中，若被提取知识的专家队伍有变化，相应的指标体系和模型参数会稍微有所差别，但不会有本质的不同。由于云南地区本身环境差异极为显著，在向云南其它区域移植本方法时，需要重新组织相应区域的专家进行具体知识的提取，否则得出的结果可能与实际有较大偏离。

对滑坡敏感性综合值的计算，充分考虑了地理环境固有的特性，采用约束算术平均法对评估地点的滑坡敏感性综合值进行推断，在很大程度上识别了理论上存在的地震滑坡安全区。这种方法不仅是本文研究结果与已有研究结果有很大区别的原因，在本质上也是对风险评价理论认识的完善的一种体现。传统的风险评价更多地关注“风险”，实际上，对“安全岛”的研究应该成为风险研究的一个重要组成部分。风险研究不但要尽量识别高风险隐患区，也要充分掌握安全岛信息，这样才能为国土规划与整治提出更合理的建议。如果本文采用简单的算术平均法进行滑坡敏感性综合值计算，得到的低值区域范围应该变小，相应的后续的滑坡敏感性分级结果也会有变化。

滑坡敏感性分级对区域风险减轻有重要信息支撑，不同分级方法带来的结果会存在较大差别。本文采用的自然断点法是根据区域滑坡敏感性推断值的一种分类，这种分类不受人为知识的干扰，完全是基于数据本身的一种客观分级。若采用类似三峡研究区的主观定义分级方法，结果会有不同，相应的各滑坡敏感性水平区域的范围、滑坡密度都会发生变化。

4 结论

本文选取滇西南的南涧和凤庆—昌宁两个研究区，开展基于GIS和专家知识的滑坡敏感性模糊逻辑评价，并进行适用性的检验。研究结果统计检验显示，南涧地区的Z值为4.1，相应的P值小于0.001，这表明，通过模型计算得到的滑坡敏感性值是该研究区滑坡事件的良好指标;凤庆—昌宁地区的Z值为8.93，相应的P值小于0.001。根据2个研究区的滑坡敏感性分布情况，可以将区域滑坡敏感分布分为4种类型区：高值和高值相连类型区、低值和低值相连类型区、低值围绕高值类型区、高值包围低值类型区。

采用自然断点法，根据研究区滑坡敏感性综合值的分布，将滑坡敏感性划分为5个等级：极低（0.0～0.001）、较低（0.001～0.051）、中等（0.051～0.394）、较高（0.394～0.557）和极高（0.557～1.0）。通过对比不同滑坡敏感性水平区域历史滑坡密度的不同来评价模型的物理效能。滑坡敏感性等级为极低和较低的地区没有发现历史滑坡记录，滑坡敏感性等级为中等地区的滑坡密度非常低，约为滑坡敏感性等级属于较高区域的1/4，为滑坡敏感性等级属于极高区域的1/10。这表明计算得到的滑坡敏感性值可用于预测某地区未来發生滑坡的可能性。在南涧地区建立的滑坡敏感性模型可以用于滇西南其它地区的滑坡敏感性推断。

参考文献：

丁星妤，戴塔根，包从法，等.2011.云南滇中地区地质灾害防治区划[J].中国地质灾害与防治学报，22（2）：69-75.

杜玉龙，方维萱.2009.云南省东川铜矿区主要地质灾害与致损机制防控[J].矿产与地质，（5）：480-486.

胡金，李波，唐立梅.2007.云南省鲁甸县地质灾害特征与成因研究[J].地质灾害与环境保护，（4）：15-19.

胡金，李波，杨艳锋.2008.GIS 在云南鲁甸县地质灾害易发性分区中的应用[J].灾害学，（1）：73-75，87.

纪甲子，陈爱兵，李俊，等.2010.云南省剑川县地质灾害调查及成因分析[J].云南地质，（4）：471-474.

李英，冯彦，周火艳.2009.怒江干流（云南段）滑坡灾害危险性分析[J].云南地理环境研究，21（6）：18-21.

李志斌，郑成德.2000.滑坡、泥石流危险度评判的灰色模式识别理论与模型[J].系统工程理论与实践，（5）：128-132.

刘丽，王士革.1995.云南昭通滑坡泥石流危险度模糊综合评判[J].山地研究，14（4）：261-266.

吕勇，黄晨晖，陈阵.2010.云南文山县地质灾害易发程度分区评价[J].地质灾害与环境保护，（4）：24-27.

钱晶，王瑞兵.2009.云南省祥云县地质灾害易发分区研究[J].昆明冶金高等专科学校学报，（5）：13-18.

孙黎丽，李波，刘江波.2007.云南省大关县泥石流形成条件及防御对策研究[J].资源环境与工程，（4）：416-419.

唐川，周钜，朱静.1994.云南崩塌滑坡危险度分区的模糊综合分析法[J].水土保持学报，（4）：48-54.

唐川.2004.金沙江流域（云南境内）山地灾害危险性评价[J].山地学报，22（4）：451-460.

陶云，唐川，段旭.2009.云南滑坡泥石流灾害及其与降水特征的关系[J].自然灾害学报，18（1）：180-186.

田志萌，张渊，郭睿，等.2011.云南省曲靖市麒麟区地质灾害特征及防治措施[J].西部探矿工程，（11）：121-123，127.

万石云，李华宏，胡娟.2013.云南省滑坡泥石流灾害危险区划[J].灾害学，28（2）：60-64.

谢洪，钟敦伦，何一平，等.2007.金沙江下游云南小江流域山地灾害综合区划[J].山地学报，25（5）：622-628.

颜春达，温钦舒，武绍周.2017.东川地质灾害特征浅析[J].工程勘察，S（1）：154-157.

尹诗琪，王冬冬，徐星安，等.2012.云南省思茅区地质灾害发育特征及防治对策[J].四川地质学报，（3）：339-342，363.

于丰泽，武蕾.2012.云南大理滑坡应急治理措施效果分析[J].四川建筑，32（4）：108-112.

翟倩倩，吴加权，叶飞，等.2016.云南哀牢山中段滑坡灾害多指标预警研究[J].昆明理工大学学报（自然科学版），41（4）：38-44.;

张超，陈艳，张宇飞，等.2016.基于多元线性回归模型的云南昭通地质灾害易发性评价[J].水文地质工程地质，（3）：159-163.

周松林，谈树成，蒋顺德，等.2010.云南省保山市隆阳区地质灾害空间分布规律及易发性分区与评价[J].地球与环境，（3）：351-356.

朱阿兴，裴韬，乔建平，等.2006.基于专家知识的滑坡危险性模糊评估方法[J].地理科学进展，25（4）：1-12.

Aleotti P，Chowdhury R.1999.Landslide hazard assessment：summary review and new perspectives[J].Bull Eng Geol Environ，58：21-44.

Alexander D E.2008.A brief survey of GIS in mass-movement studies，with reflections on theory and methods[J].Geomorphology，94（1-3）：261-267.

Atkinson P M，Massari R.1998.Generalized linear modeling of landslide susceptibility in the Central Apennines，Italy[J].Computers & Geosciences，24（4）：373-385.

Brabb E E.1984.Innovative approaches to landslide hazard and risk mapping[C]//Proceedings of the Fourth International Symposium on Landslides，Proc 4th International Conference and Field Workshop on Landslides.Publ Tokyo：Japan Landslide Society Japan，17-22.

Burrough P A.1989.Fuzzy mathematical methods for soil survey and lands evaluation[J].J Soil Sci，40（3）：477-492.

Carrara A，Cardinali M，Detti R，et al.1991.GIS techniques and statistical models in evaluating landslide hazard[J].Earth Surf Process Landf，16：427-445.

Carrara A，Pike R J.2008.GIS technology and models for assessing landslide hazard and risk[J].Geomorphology，94（3-4）：257-260.

Carrara A.1988.Landslide hazard mapping by statistical method：a “black-box” model approach[C]//Siccardi F，Bras R L.Natural Disasters in European Mediterranean Countries，Colombella，Perugia，Italy，205-224.

Chung C F，Fabbri A G，van Westen C J，1995.Multivariate regression analysis for landslide hazard zonation[C]//Carrara A，Guzzetti F.Geographical Information Systems in Assessing Natural Hazards.Dordrecht，The Netherlands：Kluwer Academic Publishers，107-133.

Dai F，Lee C F.2002.Landslide characteristics and slope instability modeling using GIS，Lantau Island，Hong Kong[J].Geomorphology，42（3-4）：213-228.

Donati L，Turrini M C.2002.An objective method to rank the importance of the factors predisposing to landslides with the GIS methodology：application to an area of the Apennines （Valnerina; Perugia，Italy） [J].Eng Geol，63（3-4）：277-289.

Ermini L，Catani F，Casagli N.2005.Artificial neural network applied to landslide susceptibility assessment[J].Geomorphology，66（1-4）：327-343.

Fisher P.1989.Knowledge-based approaches to determining and correcting areas of unreliability in geographic databases[C]//Goodchild M，Gopal S.Accuracy of Spatial Databases.Taylor & Francis，London，45-54.

Fourniadis I G，Liu J G，Mason P J.2007.Landslide hazard assessment in the Three Gorges area，China，using ASTER imagery：Wushan-Badong[J].Geomorphology，84（2）：126-144.

Guzzetti F，Reichenbach P，Cardinali M，et al.2005.Probabilistic landslide hazard assessment at the basin scale[J].Geomorphology，72（1-4）：272-299.

Hudson B D.1992.The soil survey as paradigm-based science[J].Soil Sci Soc Am J，56：836-841.

Lan H X，Zhou C H，Wang L J，et al.2004.Landslide hazard spatial analysis and prediction using GIS in the Xiaojiang watershed，Yunnan，China[J].Eng Geol，76（1-2）：109-128.

Lee S，Choi J.2004.Landslide susceptibility mapping using GIS and the weight-of evidence model[J].Int J Geogr Inf Sci，18：789-814.

Liu J G，Mason P J，Clerici N，et al.2004.Landslide hazard assessment in the Three Gorges area of the Yangtze River using ASTER imagery：Zigui-Badong[J].Geomorphology，61（1-2）：171-187.

Luger G F.2005.Artificial intelligence：Structures and strategies for complex problem solving[M].New York：Addison-Wesley，903.

MacMillan R A，Pettapiece W W，Nolan，et al.2000.A generic procedure for automatically segmenting landforms into landform elements using DEMs，heuristic rules and fuzzy logic[J].Fuzzy Sets Syst，113（1）：81-109.

Oguchi T.1997.Drainage density and relative relief in humid steep mountains with frequent slope failure[J].Earth Surf Process Landf，22（2）：107-120.

Remondo J，Oguchi T.2009.GIS and SDA applications in geomorphology[J].Geomorphology，111（1-2）：1-3.

Shi X.2002.A case-based reasoning approach to fuzzy soil mapping[D].Madison，Wisconsin：University of Wisconsin.

Van Westen，C J，van Duren I，Kruse，H M G，et al.1993.GISSIZ：Training package for geographic information systems in slope instability zonation[M].Enschede，The Netherlands：ITC Publication No.15，ITC.

Zhu A X，Wang R X，Qiao J，et al.2004.Mapping landslide susceptibility in the Three Gorges area，China using GIS，expert knowledge and fuzzy logic[M]//Chen，Yangbo.GIS and remote sensing in hydrology.Water Resources and Environment，IAHS Publication 289 （IAHS Red Book），Wallingford，UK：International Association of Hydrological Sciences，385-391.

A Fuzzy Logic Modeling of Landslide Susceptibility Mapping in SouthwestYunnan Province Based on GIS and Expert Knowledge

BAI Xianfu1，2，DAI Yuqian1，YE Liaoyuan1，NIE Gaozhong3，XU Shuo2，LUO Weidong2，YU Jiang2，XU Xin2

（1.Faculty of Geography Science，Yunnan Normal University，Kunming 650050，Yunnan，China）

（2.Yunnan Earthquake Agency，Kunming 650224，Yunnan，China）

（3.Institute of Geology，China Earthquake Administration，Beijing 100029，China）

Abstract

In order to fully identify and effectively reduce the risk of landslide hazards，we presented an approach to landslide susceptibility mapping in southwest Yunnan Province based on the expert knowledge.The approach was tested in two study areas in southwest Yunnan：Nanjian（about 470 km2）and Fengqing-Changning（about 2 300 km2）.The performance of our approach was evaluated by examining if the mean value of the computed susceptibility values at landslide sites was statistically different from that of the entire study area.A Z-score test was used to examine the statistical significance of the difference.The computed Z-score for the Nanjian area was 4.1 and the corresponding P-value was less than 0.001.This suggested that the computed landslide susceptibility values were good indicators of landslide occurrences.In the Fengqing-Changning study area，the computed Z-score was 8.93 and the corresponding P-value was less than 0.001.In addition，we divided the susceptibility value into five levels by the Natural Break Point method.The result sets like：very low（0.0-0.001），low（0.001-0.051），moderate（0.051-0.394），high（0.394-0.557）and very high（0.557-1.0）.No landslides were found in areas of very low and low susceptibility.Landslide density was about four times higher in areas of very high susceptibility than that in the high susceptibility areas，and about 10 times as high as that in the moderate susceptibility areas.Results from these case studies suggest that our approach based on expert knowledge is workable in mapping landslide susceptibility and that its performance is maintained when it is applied to a new area.

Keywords：landslide susceptibility;expert knowledge;Fuzzy Logic modeling;Constrained Arithmetic Mean method;southwest Yunnan Province