基于符号动力学的开关变换器状态分析
冯锦澎
(广州大学 广东省广州市 510400)
1 引言
DC-DC 开关功率变换器作为现代设备不可或缺部分,对其动力学规律和稳定性分析在设计和实际应用研究中都有着十分种要意义。DC-DC 开关变换器是一种典型强非线性系统,对其建模有三种代表性方法:离散迭代非线性映射模型;分段光滑系统的微分方程模型;加权平均连续时间平均模型。第一种方法以系统状态变量为研究着眼点,易于全面分析电路系统的动力学性质,如不动点及各种周期轨道的边界条件。第二种方法的方程解反映了真实的物理特性,却不能用解析方法分析动力学行为的各种稳定定性。一般只能用数值方法求解。最后一种方法只能适用于低频分析。[1]
开关变换器出现非稳定现象如分岔和混沌研究一般采用前面两种模型。前者通过仿真得到分岔图,根据图形来判断分岔及混沌的条件;后者采用Lyapunov 指数方法,通过计算开关变换器变量参数,得到李氏指数的符号,根据李氏指数符号的正负来判断该系统稳定还是混沌。不管是哪种方法以,都离不开大量数值计算。也有学者从数学理论中的迭代映射模型倍周期分岔定理出发,撇开具体的物理结构来推导开关变换器的稳定性条件。[2]
这些分析方法都离不开数学理论推导,在工程上缺少易用性。符号动力学是一种对现实物理系统进行粗粒化和离散化,在有限精度下对动力学过程实行严格描述的一种方法。对复杂系统得到简单的符号时间序列就可以刻画出系统特征的方法。本文利用符号动力学这种分析方法,对不连续导电模型DC-DC 开关变换器进行实用符号动力学分析,得到其揉序列表及各序列对应参数值。与分岔图和Lyapunov 指数法进行比较,得出一种新的实用稳定性判据,并在最后验证该方法的可行性。
2 开关变换器符号动力学分析
最初的符号动力学是一种 J.Hadmard M.Morse(莫尔斯)在 19世纪末提出来的,基于粗粒化的拓扑方法。将这种方法运用于实际物理系统的状态特点分析中,就是实用符号动力学方法。[3]
2.1 DCM电压反馈型开关变换器迭代模型
电压型 BUCK 变换器原理图如图 1所示。其迭代映射方程:[4]
其中 E 输入电压,T 为开关周期,L 为输入电感,R 为负载电阻,C 为输出滤波电容,X 为期望的稳态输出电压,K 是反馈比例增益,D 为稳态占空比。xn 代表第 n 次迭代的电容电压,其他参数表达式如下:
该迭代映射是一根倒峰曲线,如图 2所示。该曲线与Y=X 直线相交点就是平衡点 X*。

图2:BUCK 变换器K=0.1211 映射曲线
实用符号动力学的排序规则是:以映射的单调性对相空间进行划分。图 2 中的极小点 C 为界,把相空间划分为左右两部分。C 左边记为 L,右边记为 R。初始值 X0 为起点,根据公式 1 进行迭代,每次迭代得到一个相对应的符号 R 或L,刚好等于 C 则记为 C。按此规则把依次得到的符号按时间顺序排列起来就得到一个半无穷 符号序列S1S2S3…Sn…,其中
仿照实数排序方法,我们把一位的符号序列记为:
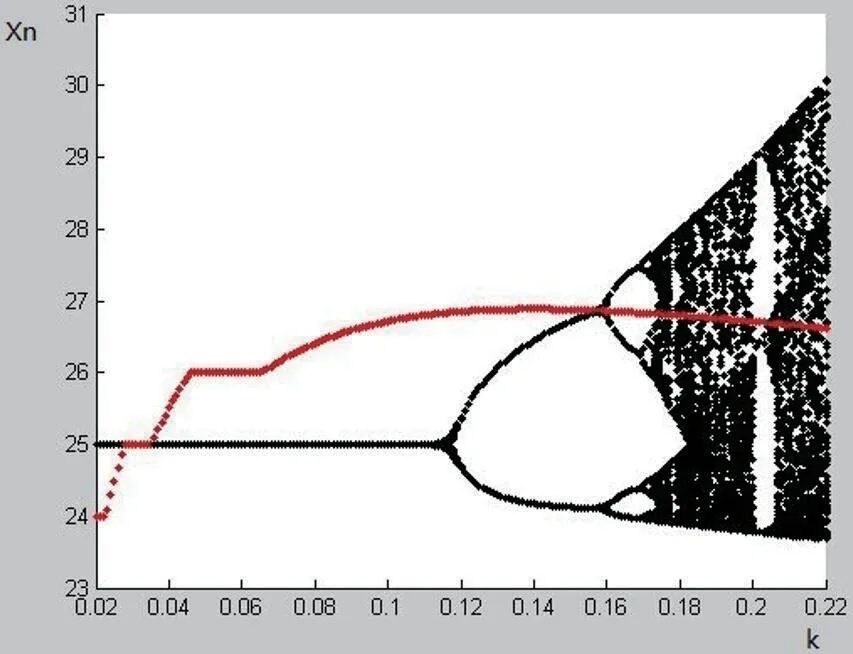
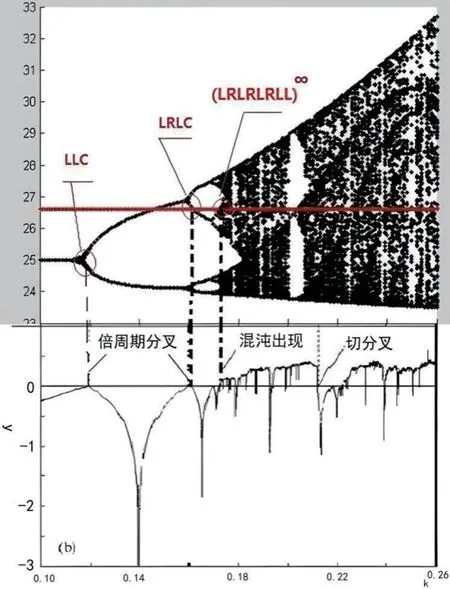
L 考虑二次迭代时,L 部分映射为单调降,R 部分映射为单调升。有如下关系: LR 如此类推,当ΔE表示含有偶数个 L 的序列;ΔO表示含有奇数个 L 序列时有: ΔOR<ΔOC<ΔOL; ΔEL<ΔEC<ΔER BUCK 变换器的最大符号序列为R∞;最小符号序列是LR∞。 BUCK 变换器在 K 不变情况下,迭代结果不可能低于谷底的临界点 C 对应的 f(C),实际系统中最大范围不可能大于电源 E。我们把大于 E,小于 f(C) 为 BUCK 变换器基本禁区。临界点 C,截止点 E 对应的一次迭代像点对应的序列称为该系统揉序列。允字条件就是一个充许序列任意移位都不能落入基本禁止区。如图 2 中红框以外。 BUCK 变换器映射曲线是倒峰映射,C 两端任一点出发得到的迭代值都应该大于极小值 f(C),其对应符号序列都应该比 f(C)序列大,该 f(C)序列具有移位最小性,称为BUCK 变换器揉序列 K。 依据符号动力学周期窗口定理[3],我们可以得到 BUCK变换器的中介字产生方法。 (1)在两个序列中产生 S1 上序列 S1+,S2 下序列S2-。 (2)比较 (S1+)(S1+)…和(S2-)(S21)中重复部分M。如果M 长度大于S1+,则去掉M 最后一个重复字符直接成为中介字。 (3)如M 不超过 S1+长度,则在计算M 奇偶,如果S1+ (4)检查新产生中介字如果与S1 相等,则没有新中介字。如果与S2 相等,则用 S2-作为新中介字 。 图 3所示就是由该算法由程序自动产生的5 级超稳揉序列表(MSS)。 图3:BUCK 变换器5 级MSS 表 对于给出一个超稳揉序列,我们可以通过字提升法找出系统对应的参数。例如对K=RLRC 时,BUCK 变换器映射公式(1),令Xn 为自变量 x,Xn+1 为因变量 y,k 为可变参数。按实际电路确定各元件参数如表 1所示。 表1:DCM DC-DC BUCK 变换器参数 则公式形式变为: 则符号 R、L 分别为两支逆函数: 对于符号序列 LRLC 有 x*为平衡不动点。这里取 25V。 从而求得对应 k=1.591400e-01,同理求得LRC 对应k=3.3532e-02。从中我们可以看出不同的揉序列可以刻画出不同的轨道周期。 以BUCK 变换器反馈系数k 为横轴变量,迭代结果Xn为纵轴变量,画出该映射分岔图如图 4 看示,其中红色线是k 值下所对应的临界点轨迹曲线。 图4:BUCK 变换器映射对应的分岔图 图8:k=0.133 时相图和iL、Vo 波形仿真结果 从图中很容易看出:在k=0.0353 附近时,映射临界点C 刚好与超稳不动点(X*=25)重合,是1 级超稳揉序列C所对应轨道。数学上该点斜率为零且收剑速度最快。k 在(0.0353,0.1189)范围内是1P 轨道范围,这时候为 2 级揉序列LC 所对应轨道。k 在(0.1189,0.159)2P 轨道范围,就是发生倍周期分岔范围,这时是 3 级揉序列 LLC 所对应轨道。k 在(0.159,0.173)4P 轨道范围,就是发生 4周期分岔范围,这时是 4 级揉序列LRLC 所对应轨道。在k>0.173 开始就是非周期轨道范围,这时是(LRLRLRLL)∞符号序列所对应轨道。把该参数k 所对应轨道序列作表归纳如表 2所示。 表2:BUCK 变换器参数k 对应符号序列表 符号动力学中表示进入混沌的符号序列格式是ρλ∞,即出现周期 3 意味着混沌出现[3]。而当 k=0.173 时,出现(LRLRLRLL)∞,经等价转换可以等价表示为 L(RLRLRLLL)∞形式,该序列满足 ρλ∞形式,也就是 BUCK 电路开始进入沌混。因此我们可以通过 BUCK 变换器电路产生的符号序列来判断电路当前状态。典型的符号序列出现可以看作非稳定边界条件的出现。 变换器稳定性分析,很多学者已经通过Lyapunov 指数法、分岔图法、分段光滑建立微分方程求解、从倍周期分岔数学定理等方法研究比较透切[4],但使用符号动力学方法从符号序列判断稳定性边界条件还很少出现相关研究文章。现把本文研究结果与其他学者研究 Lyapunov 指数的结果进行对比,结果如图 5所示。 图5:BUCK 变换器符号序列与李氏指数 图 11:k=0.155 时相图及电流电压波形实测图 图 12:k=0.252 时相图及电流电压波形实测图 从对比结果来看,当 Lyapunov 指数每次由负值经过零点变为正时引发系统发生倍周期分岔,混沌及切分岔时,映射产生的符号序列都能很好表征出该状态的变化。符号动力学分析在 BUCK 变换器状态分析中是可行的一种简单方法。 对图 1 的电压反馈型 BUCK 变换器进行 PSIM 仿真。仿真电路如图 6所示。仿真结果如图 7-图9所示。 图6:电压反馈BUCK 变换器仿真电路 图7:k=0.110 时相图和iL、Vo 波形仿真结果 图9:k=0.165 时相图和iL、Vo 波形仿真结果 以电感电流iL和输出电压Vo分别为相图的纵坐标和横坐标,得到LC、LLC、和LRLC 结果分别对应的相图和电流电压波形如图 7-图9。 在仿真基础上,我们做了一个电压反馈型BUCK 变换器实际电路,进行验证测试。实测结果分别如图 10-12所示。 图10:k=0.119 时相图及电流电压波形实测图 把符号动力学分析理论对 BUCK 变换器的状态检测结果与仿真及实测结果进行对比如表 3所示。理论值与仿真结果比较接近,实测值与理论值存在一定误差,但状态转化规律性依然明显。这是由于实际电路元件参数精确度及噪声干扰等因素所致。如何提高实际电路检测精度有待以后继续研究。 表 3:BUCK 变换器状态检测三种方法比较 我们从实用符号动力学分析理论出发,利用其离散化、粗粒化的特点,对电压反馈型 BUCK 变换器状态进行了符号动力学分析,避开了复杂的计算方法及系统细节。根据超稳揉序列是对系统轨道的刻画原理,提出从 BUCK 变换器产生的符号序列作为其当前状态判断依据。并把该结果与其他传统分析方法结果进行比较,证明本文提出的基于符号动力学分析方法的可行性。并从仿真和实验验证角度对符号动力学结果进行了验证,也证明了这是一种可行的稳定性边界条件判定方法。为工程上 DC-DC 开关功率变换器混沌行为检测提供相对简便可行的新方法。2.2 揉序列及MSS表
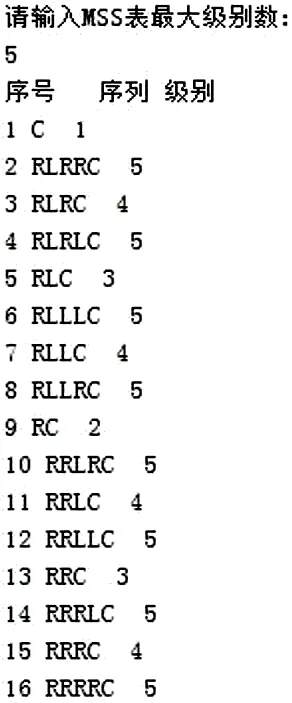
2.3 字提升法确定参数

2.4 分岔图中分岔与混沌边界的对应揉序列


2.5 符号动力学分析结果与 Lyapunov 指数法结果比较

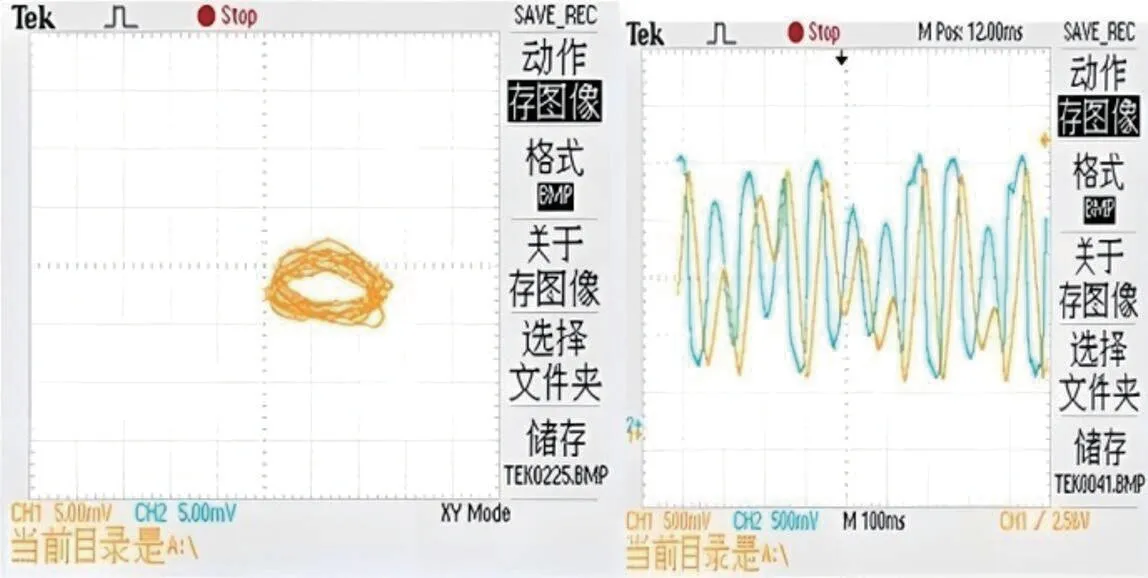
3 符号动力学分析法的实际电路验证
3.1 电压反馈型BUCK变换器状态仿真


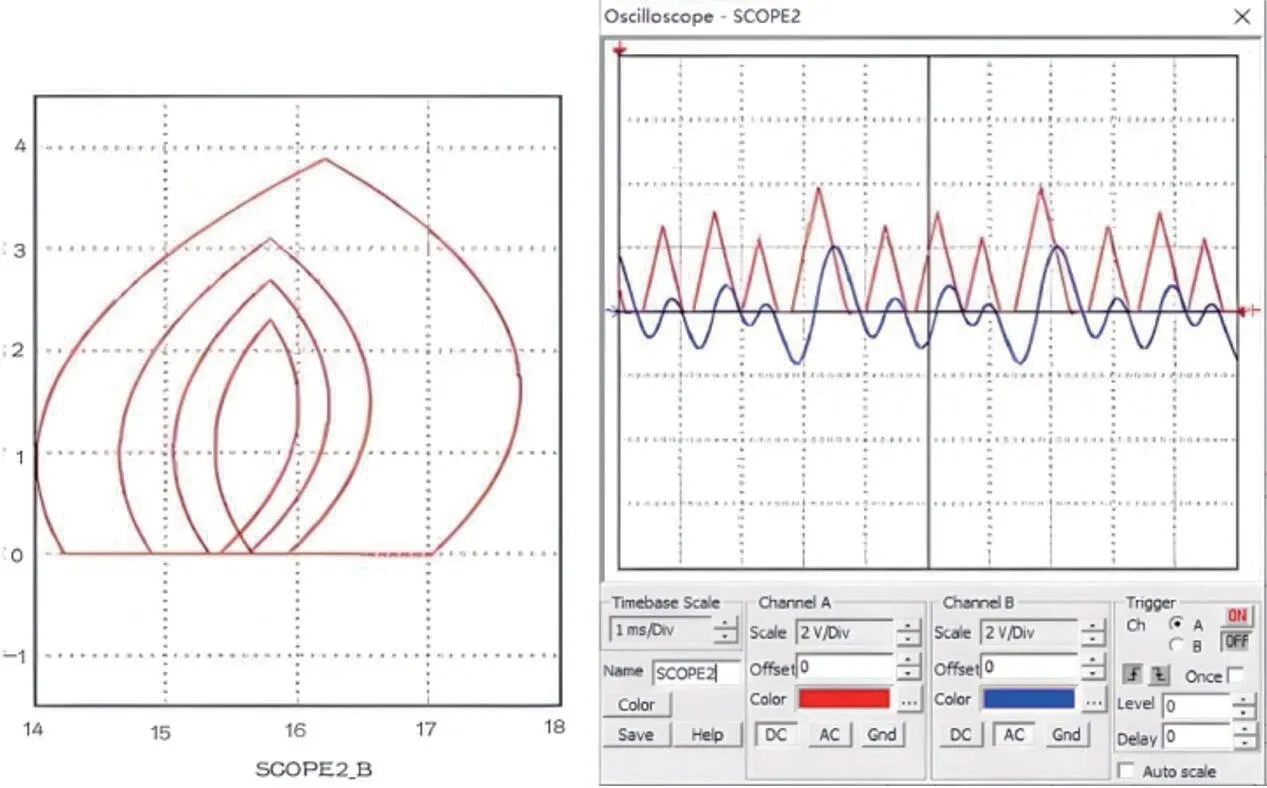
3.2 电压反馈型BUCK变换器电路验证
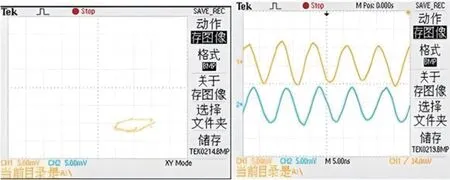
3.3 理论与验证结果对比

4 总结

