基于逆序编码的汉诺塔非递归算法

严海兵

（苏州科技大学 图书馆，江苏 苏州 215009）

汉诺塔问题源于古印度的一个游戏。游戏中有A、B、C三根柱子，A柱上从下往上按照大小顺序摞着n个圆盘。游戏的目的：把圆盘按大小顺序重新摆放到C柱上。规则为：（1）一次只能移动一只圆盘；（2）每根柱子只有最上面的圆盘可以搬动；（3）小圆盘上不能摆放大圆盘；（4）移动圆盘时可以利用B柱当作过渡柱子。

一些文献在介绍递归算法、借助堆栈转化递归算法为非递归算法等内容时往往引入汉诺塔问题作为典型实例介绍[1－2]。一些学者在提出新的程序算法思路时，也常用汉诺塔问题的解决作为验证实例。如文献[3]利用二叉树的中序遍历深入理解程序递归算法；文献[4]利用状态机的思想提出的非递归算法，避免堆栈内存溢出问题；文献[5-7]化解汉诺塔问题为抽象分层树，利用树分层次迭代的非递归算法；文献[8]利用人工智能算法中的启发式搜索，解决汉诺塔问题，尝试A算法的执行效率。

笔者通过对汉诺塔圆盘搬运过程的分析，改变传统的圆盘编码从上到下、由小到大的顺序1，2，…，n，为逆序n，n-1，…，1，通过找出圆盘移动的数学规律，提出一种新的简洁高效的非递归算法。图1为汉诺塔的圆盘顺序、逆序编码图。下文分析中所涉及的圆盘编码均按逆序编码。

图1 汉诺塔的圆盘顺序、逆序编码图

1 圆盘搬运的数学规律

汉诺塔上的圆盘按照从大到小的顺序编号1，2，…，n。当n=1时，圆盘搬运顺序为，1 A→C；当n=2时，圆盘搬运顺序为，2 A→B、1 A→C、2 B→C；当n=3时，圆盘搬运顺序见表1；当n=4时，圆盘搬运顺序见表2。

表1 3层汉诺塔搬运顺序

表2 4层汉诺塔搬运顺序

定理1完成n层汉诺塔的搬运总次数为Tn=2n-1[9]。

对于圆盘数为n层的汉诺塔可以分三步搬运：（1）将A柱上的n至2号盘，利用C柱过渡，搬运到B柱，搬运次数为Tn-1；（2）将A柱上的1号盘直接搬运到C柱上，搬运次数为1；（3）将B柱上的n至2号盘，利用A柱过渡，搬运到C柱，搬运次数为Tn-1，搬运完成。圆盘搬运总次数为Tn=2Tn-1+1，进一步利用数学归纳法可以证明Tn=2n-1。

证明当n=1，T1=1；假设Tn-1=2n-1-1成立；因为Tn=2Tn-1+1，所以Tn=2（2n-1-1）+1=2n-1，证毕。

因此，n层汉诺塔搬运的完成需要分Tn次步骤。

定理2完成n层汉诺塔的搬运，前1，2，…，n-1号圆盘的搬运次数、顺序与完成n-1层汉诺塔的搬运相同。

4层汉诺塔的搬运见表2，去除4号盘的搬运示例见表3，可以发现与表1的3层汉诺塔圆盘的搬运次数、顺序完全相同。

表3 去除4号盘的4层汉诺塔搬运顺序

n层汉诺塔的n号圆盘在A、B、C柱之间来回搬运的目的是让开通道，为了n-1层汉诺塔的搬运有序完成，因此，定理2成立。定理2是基于逆序编码的圆盘搬运规律，传统顺序编码此定理不成立。文中后续定理规律是以定理2为基础延伸的。

定理3第k号圆盘搬运总次数为dk=2k-1。

证明由定理1、定理2可得，dk=Tk-Tk-1=（2k-1）-（2k-1-1）=2k-1。

定理4在完成n层汉诺塔的搬运中，第k号圆盘搬运的步骤号为Stepk（x）=2（n-k）（2x-1），{x|x∈N，1≤x≤dk，dk=2k-1}。

由定理1可知，n层汉诺塔的搬运相当2次n-1层汉诺塔的搬运加1次底层1号圆盘的搬运。底层1号圆盘的搬运顺序号在第一次n-1层汉诺塔的搬运结束后进行，因此，为Step1=（Tn+1）/2=2n-1。以此类推，k号圆盘的首次搬运的步骤号是在其上n，n-1，…，k+1个圆盘组成的汉诺塔搬运第一次搬运结束后进行，因此，为Stepk（1）=2n-k。

每个圆盘在总的搬运序列中是平均分布的，由定理3可知，第k号圆盘搬运总次数为dk=2k-1，由定理1可知，n层汉诺塔的搬运总次数为Tn=2n-1。因此，k号圆盘搬运步骤间隔为（Tn+1）/dk=2n-k+1。因此，在完成n层汉诺塔的搬运中，第k号圆盘搬运的步骤号为

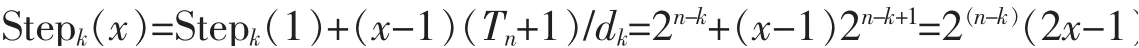
其中x为k号圆盘的搬运次序，因此，x取值为1，2，…，dk，所以，{x|x∈N，1≤x≤dk，dk=2k-1}。

定理5n层汉诺塔的搬运，奇数号盘按照A→C、C→B、B→A顺序循环搬运，偶数号盘按照A→B、B→C、C→A顺序循环搬运，直到搬运结束。

由表2可知，4层汉诺塔第1号盘搬运为A→C，第3号盘搬运为A→C、C→B、B→A、A→C，符合奇数号盘按照A→C、C→B、B→A顺序循环搬运。第2号盘搬运为A→B、B→C，第4号盘搬运为A→B、B→C、C→A、A→B、B→C、C→A、A→B、B→C，符合偶数号盘按照A→B、B→C、C→A顺序循环搬运。依据定理2，可以证明定理5成立。

2 算法实现

2.1 算法思路设计

输入：汉诺塔的圆盘层数n，定义柱子编号“A”、“B”、“C”。

输出：2n-1次搬运步骤全过程。

步骤：循环控制整数k从1到n，分析每只圆盘的搬运情况，执行下列步骤：

Step1：计算第k号圆盘搬运总次数为dk=2k-1；

Step2：计算第k号圆盘首次搬运的步骤号Stepk（1）=2n-k；

Step3：循环控制k号圆盘搬运次序x从1到dk，

①如果第k号圆盘是奇数号盘，搬运次序xmod3，依据计算结果按照A→C、C→B、B→A顺序循环搬运；

②如果第k号圆盘是偶数号盘，搬运次序xmod3，依据计算结果按照A→B、B→C、C→A顺序循环搬运。

2.2 C程序代码实现

定义n层汉诺塔的数据类型HanoiType，N表示汉诺塔圆盘的层数。定义圆盘搬运的数据类型Result，first、last分别表示被搬运圆盘disk起始柱、目标柱位置。

因为程序算法中涉及指数函数2n计算较多，因此定义整数型函数npower2（n）计算2n。

2.3 算法时间空间复杂度

基于逆序的汉诺塔非递归算法的时间复杂度T（n）=21-1+22-1+23-1+…+2n-1=2n-1=O（2n），这与递归算法的相当。在空间复杂度S（n）方面，由于算法中需要建立数量为2n-1的数组存储空间，因此S（n）=O（2n）。考虑到递归算法中统一改屏幕打印显示为数组存储，其空间复杂度也是相当的。基于逆序的汉诺塔非递归算法在时间空间的复杂度上没有优势。传统汉诺塔算法都是按照圆盘的序号依次顺序寻找搬运规律的，该项目研究中笔者掌握了每个圆盘的每次的搬运的数学规律，因此，可以随机寻找出任意号圆盘的任意次搬运规律，由于没有基本的堆栈运算，在基础运算上具有部分优势。下面定义的函数void find（）屏幕打印k号圆盘的第x次的搬运规律。

3 运行时间测试

运行文中所写程序算法的计算机配置信息：操作系统Windows 7（64位操作系统，专业版），处理器一个Intel（R）Core（TM）i3-2120 CPU@3.3CHz 3.30GHz，内存4.00GB。每次运行程序测量的时间有误差，记录的运行时间为运行3次后取平均值。为了测试文中基于逆序编码的汉诺塔非递归算法的执行效率，进行了三种汉诺塔算法的运行时间比较测试，分别是文中基于逆序编码的非递归算法、传统的经典递归算法、借助堆栈实现的非递归算法。因三种算法中用于屏幕显示的语句相同，为屏幕打印printf语句，考虑到屏幕打印语句运行的耗时较长，约占运行测试时间的80%，对三种算法执行效率的比较有较大干扰，表4中统计的测试时间数据是统一去除屏幕打印printf语句后的程序运行时间[10]，时间单位为秒。因计算机测试的时间最小精度为0.001 s，为便于观测，问题规模即汉诺塔的层数n从10开始试验计数统计。当n＞27时，程序运行停止。由表4可知三种算法随着问题规模（n）的增大，程序算法运行所需时间都为2的指数级增长。该文研究的基于逆序编码的非递归算法，执行效率优势明显。

表4 三种汉诺塔程序算法的运行时间 单位：s

4 结语

汉诺塔问题的求解是很多程序算法思想的试金石，文中的算法是其中一次新的探索。汉诺塔圆盘逆序编码后所呈现出的移动数学规律，比顺序编码的要更加清晰、富有规律，通过其数学定理推导，得出的非递归程序算法运行效率较高。传统的汉诺塔算法只能顺序求解每个圆盘的搬运规律，现在可以随机的寻找出任意圆盘任意次序的搬运规律。一些需要通过递归调用或者借助堆栈解决的程序算法，或明或暗也有相似的顺序编码问题，文中的算法可以提供借鉴和启迪作用。