单模式LIPS-200离子推力器的寿命及可靠性定量评估
张雪儿,张天平,李得天
(1. 兰州空间技术物理研究所, 兰州 730000; 2. 真空技术与物理重点实验室, 兰州 730000;3. 甘肃省空间电推进技术重点实验室,兰州 730000)
0 引 言
电推进在航天工程中有广泛的应用。LIPS-200为首款完成地面寿命试验验证和空间飞行试验,并开始应用于我国DFH-3B平台和DFH-4E平台卫星型号的单工作模式离子推力器产品,其额定工作模式(工况)性能为输入功率1 kW、推力40 mN、比冲3000 s。兰州空间技术物理研究所正在进行三方面的LIPS-200研制工作:1) LIPS-200产品成熟度提升到6级水平; 2) LIPS-200A产品工作寿命延长到20 kh; 3) LIPS-200E性能扩展到输入功率1.5 kW、推力60 mN、比冲3000 s并实现双工作模式。其中,LIPS-200产品成熟度提升到6级水平的技术工作重点是推力器产品的寿命及可靠性定量评估。
离子推力器产品工作寿命及可靠性的定量评估是一个具有较大技术挑战的难题,其主要原因包括:1)离子推力器寿命一般都长达数万小时以上,推力器工况参数和环境条件参数(统称为输入参数)的较小初始值差异,可能会导致最早失效模式和相应寿命结果的较大差别;2)受时间周期长、花费成本高及设备资源有限等约束,离子推力器完成寿命试验验证的子样数只有1台或2台;3)离子推力器为典型的多种失效模式共存的产品,一方面推力器工作过程中各失效机制均在发生作用,另一方面哪一种失效模式最早出现又与输入参数的不确定度及敏感度相关;4)从推力器各失效模式对应的失效机制及其磨损模型来看,大部分磨损模型为确定性的,少部分模型为随机性的;5)对于多工作模式离子推力器,工作模式与失效模式之间的耦合使得情况变得更为复杂。
针对离子推力器寿命及可靠性定量评估难题,结合单工作模式LIPS-200离子推力器产品成熟度提升需求,本文通过对离子推力器失效模式、工作输入参数和工程应用任务剖面三方面要素的耦合分析,基于试验验证数据、模型计算数据和数理统计规律等方法,首次提出了单工作模式离子推力器寿命及可靠性定量评估的技术途径,并给出了LIPS-200离子推力器的典型算例。
1 离子推力器的失效模式与磨损模型
1.1 失效模式及其特征参数和判据
已经被国内外寿命试验所验证的会切磁场离子推力器的主要失效模式如表1所列,用FM标记失效模式(FM为失效模式,为失效模式序号),=1,2,…,14。表1中还给出了失效模式对应的推力器产品部组件和简要失效机制描述。

表1 会切磁场离子推力器的主要失效模式Table 1 Main failure modes of cusped field ion thruster
对于每一种失效模式FM都存在与之对应的失效特征参数及其失效阈值(临界值),当特征参数值达到失效临界值时就认为推力器已经失效且寿命终结,可表达为:
=T,=1,2,…,14
(1)
式中:C为FM对应的失效特征参数(Characteristic parameter); CT为FM对应的失效特征参数阈值(Characteristic parameter threshold)。
例如,栅极发生电子反流失效的特征参数为电子反流极限,失效判据为加速电压,当电子反流极限绝对值大于加速电压绝对值时,就一定会发生电子反流失效,推力器寿命终结,也就是对应FM5的寿命终结(简称寿终)判据为:

(2)
式中:为电子反流极限;为加速电压。确定或测量电子反流极限的条件为反流电子电流达到束电流的0.1%。
1.2 失效机制及其磨损模型
设想对单一工作模式离子推力器进行了寿命试验,寿命终结对应的失效模式为FM,则寿命试验的寿终判据、工作时间和工作寿命之间的关系可以用如下函数关系表达:
T=(,)|=
(3)
式中:为累计工作时间;为推力器工作寿命;为输入参数集合。等号右边为失效模式FM所对应的磨损模型,也就是失效特征参数随输入参数和累计工作时间的变化关系。式(3)的物理意义为:当失效特征参数值达到失效临界值时推力器寿命终结,对应的累计工作时间为本次寿命试验结果。
例如,对FM2失效模式导致的寿命终结,失效特征参数为被交换电荷离子溅射腐蚀掉的加速栅局部材料质量,失效临界值为加速栅局部原有材料质量的一半。LIPS-200推力器对应的磨损模型为显函数:

(4)
式中:()为加速栅材料的电荷交换离子溅射产额;为加速栅材料原子质量;d/d为入射(碰撞)于加速栅局部表面的电荷交换离子数通量。可见磨损过程与累计工作时间呈线性关系,输入参数有3个,即=,, d/d。对应式(3)可推导出推力器寿命为:

(5)
式中:为加速栅材料密度;为加速栅初始厚度;为加速栅孔间距;为加速栅初始孔径。等号右边分子为失效临界值表达式。可见FM2失效模式所决定的推力器寿命为7个输入参数的函数。
1.3 工程失效模式和关键失效模式
就离子推力器产品的设计及验证而言,并不是每个失效模式都决定着离子推力器的寿命。在推力器工作过程中最早出现的失效模式称为关键失效模式,也就是关键失效模式对应推力器寿命的最短板。对每个FM定义其寿命裕度为:

(6)
式中:为寿命裕度;为最短板寿命。显然,对关键失效模式寿命裕度为1,其他失效模式寿命裕度均大于1。
定义寿命裕度处于[1.0, 1.5]区间的离子推力器失效模式为工程失效模式,可见所谓工程失效模式就是指工程产品实际应用中发生可能性较大、有必要重视的失效模式。离子推力器工程失效模式和关键失效模式的确认及验证,一般采用中期试验方法进行,即离子推力器在额定工况下累计工作一定时间,试验结束后根据各失效特征参数的变化情况,结合磨损模型进行从试验累计工作时间到最低目标寿命及极限寿命的线性外推,即可得到对应失效模式的寿命裕度为:
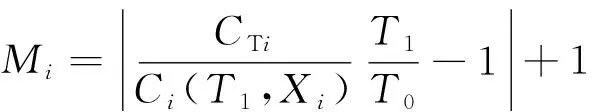
(7)
式中:为试验累计工作时间,一般取最低目标寿命的10%~15%。
LIPS-200离子推力器通过额定工况下的寿命试验验证,确认其关键失效模式为FM2,相应寿命为=14649 h。寿命试验结束后进行的产品破坏性解剖及检测分析表明,LIPS-200的工程失效模式为FM1、FM5、FM7,其他失效模式的寿命裕度均大于1.5。从产品设计角度分析,FM3和FM10可以通过防止溅射沉积物剥离或控制剥离物尺寸来有效避免;FM4失效可以通过控制非预期电击穿过程中的能量沉积来避免;FM6失效模式可以通过发射体裕度设计和氙气纯度控制使其对应的寿命裕度达到2倍以上;FM8和FM9可以通过合理的几何设计和羽流模式流率裕度设计来有效抑制,使其对应的寿命裕度达到2倍以上;FM11失效模式可以通过加热器设计使其对应的寿命裕度达到4倍以上;FM12失效模式可以通过降低放电电压及其震荡幅度、减少双荷离子产额来有效抑制,使其对应的寿命裕度达到2倍以上;FM13失效模式可以通过屏蔽式或迷宫式绝缘器设计来消除;FM14失效模式可以通过采用高温永久磁铁和合理的温度降额设计来避免。
LIPS-200离子推力器针对FM7失效模式完成了设计改进,通过采用石墨作为触持极材料,触持极的抗离子溅射能力提高了8倍,专项验证的改进寿命裕度达到5倍以上,因此FM7也从工程失效模式中排除。
2 离子推力器寿命不确定度及概率分布
2.1 寿命模型及函数关系
通过1台LIPS-200离子推力器的寿命试验和磨损模型预测结果,确认的工程失效模式包括FM1、FM2、FM5,其中FM2为关键失效模式。但正如引言中所述,假如用另1台LIPS-200产品再进行一次寿命试验,其寿命试验结果很可能不再是14649 h;如果试验环境条件有差异,所得关键失效模式甚至也会改变(例如真空舱内工作压力有差异时,关键失效模式可能变为FM5)。由此可见,如果进行多台离子推力器的寿命试验,其寿命试验结果应当在一定范围内分布。
离子推力器的寿命分布范围主要取决于确定性磨损模型中输入参数的不确定度以及非确定(随机)性磨损模型中的变量及随机函数关系。这里主要以LIPS-200产品的FM2失效模式和FM5失效模式为例进行讨论。
离子推力器加速栅结构失效对应的寿命模型为式(5),其中()的一个工程可用表达式为:

(8)
由式(5)和式(8)得到寿命模型为:

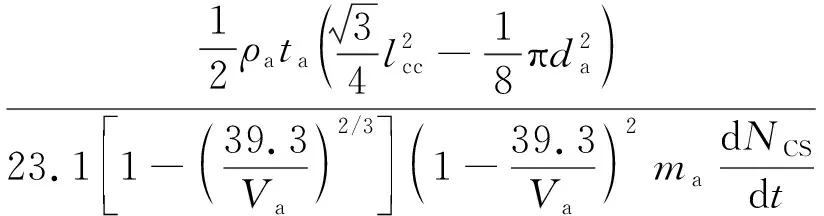
(9)
离子推力器电子反流失效对应的寿命模型为多变量隐函数,具体推导过程和表达式参见文献[10],这里不再重复。
2.2 寿命不确定度及敏感度分析
从寿命模型可见,各工程失效模式下的寿命不确定度来源于函数关系中各输入参数的不确定度,基于寿命与输入参数的函数关系,就可以根据输入参数的不确定度及其传递关系(方法)计算寿命的不确定度。按照QMU(Quantification of margins and uncertainties)工程方法理论,LIPS-200离子推力器失效寿命关于其输入参数的局域敏感度和不确定度传递关系分别为:

(10)
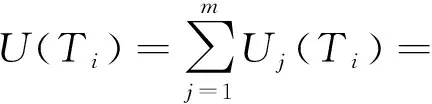

(11)

表2 LIPS-200离子推力器主要参数Table 2 Main parameters of LIPS-200
略去具体计算过程,得到LIPS-200离子推力器加速栅结构失效寿命所对应各参数的敏感度和不确定度的计算结果见表3。

表3 加速栅结构失效寿命的参数敏感度和不确定度Table 3 Parameter sensitivity and uncertainty for FM2 lifetime
从表中数据可见,在各因素中交换电荷离子数通量的不确定度贡献最大,其他参数贡献由大到小依次为孔间距、厚度、孔径和加速电压,加速栅结构失效寿命的最大不确定度为3431 h,也就是说LIPS-200推力器寿命分布区间为[10793 h,17655 h],要缩小寿命分布区间,需要进一步降低输入参数的不确定度。
2.3 推力器寿命的概率分布
从数理统计角度看,单工作模式离子推力器寿命试验结果可视为随机事件,所有寿命试验结果的样本空间为二维空间,即寿命(时间)维度和失效模式维度。对应每个失效模式FM的寿命试验结果为,随机且连续地分布于实数区域[min,max]中,min和max取决于推力器设计、输入参数的不确定度和试验环境等,例如3.2节中估算的FM2的失效寿命=10793 h、=17655 h。寿命结果达到的概率用()表示,由于离子推力器各失效模型均为非常典型的磨损性失效,故()适合用三参数威布尔分布描述为:
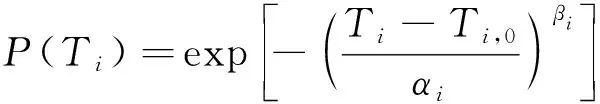
(12)
一般来说,对于不同失效模式,其标度因子、形状因子和寿命阈值,0的取值均不相同。显然,通过大量寿命试验数据来获取这些分布参数不太现实,一种可行的技术途径就是将有限的试验结果和模拟抽样计算结果相结合,这里仍然以LIPS-200的FM2失效模式为例。
用于模拟抽样计算的寿命模型可以是解析函数或数值计算模型,这里采用经试验结果校验的解析函数模型式(9)。合理假设表2中所列各工作参数的不确定度呈正态分布,对各工作参数进行随机抽样并代入式(9)计算寿命结果;总计进行500次抽样计算后,对寿命结果进行威布尔分布拟合,由此得到、和的取值。略去具体计算和拟合过程,所得概率分布结果如图1所示,其分布函数如式(13)所示。
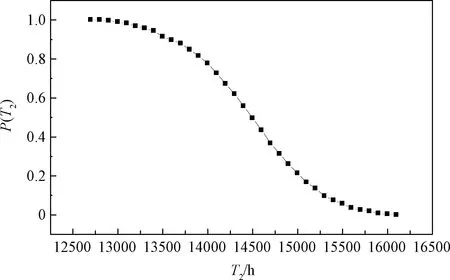
图1 LIPS-200加速栅结构失效寿命概率分布Fig.1 Lifetime distribution for FM2 of LIPS-200
()=

(13)
注意式(13)中,加速栅结构失效寿命达到12030 h或更小值的概率为1,也就是在12030 h之前推力器不可能出现FM2模式失效。
3 工程任务应用中的可靠性评估
3.1 离子推力器工作剖面
假设LIPS-200离子推力器在某一卫星型号任务中的工作剖面为,=1,2,…,,其中下标为任务工作剖面中推力器工作的阶段性顺序号,为整个任务包含的阶段数,为第阶段内的累计工作时间,完成任务对推力器的寿命要求(称为产品寿命要求)为:
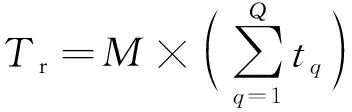
(14)
也就是寿命安全裕度和任务剖面工作时间之和的乘积,=1时为最低寿命要求(称为应用寿命要求)。例如GEO卫星上LIPS-200有三个阶段的任务,第一阶段为GEO轨道圆化和轨道捕获,累计工作约1000 h;第二阶段为15年南北位置保持,累计工作约9000 h;第三阶段为寿终卫星垃圾轨道转移,累计工作约2500 h。对于该卫星任务=3,任务工作剖面为=1000 h,=9000 h,=2500 h,应用寿命要求为12500 h,考虑1.2倍裕度时的推力器寿命要求为15000 h。
在此工作剖面基础上,就可以对任一工程失效模式进行完成阶段性任务的可靠性评估,即三个阶段的工作可靠性分别为:
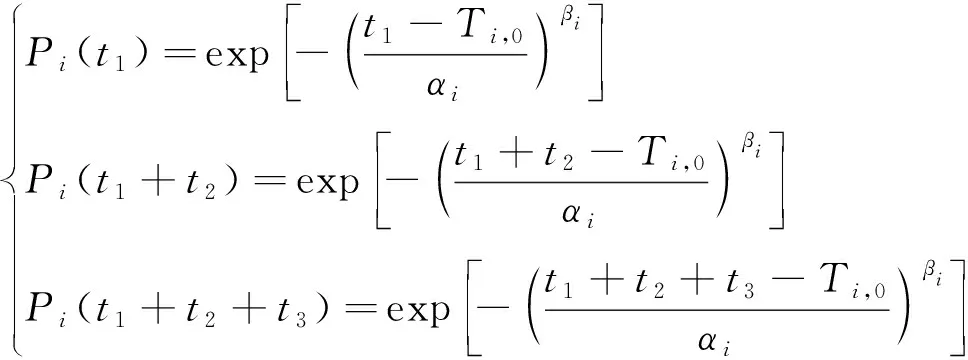
3.2 针对工程任务的可靠性评估
对某一应用单模式离子推力器的航天工程任务,在推力器工作过程中,每一种失效模式的磨损机制都在运行,由此可见推力器的失效事件是各模式下失效的和事件,而各模式下的失效为相互独立事件。基于统计学原理可得到推力器完成本次任务(寿命达到)的概率为每个失效模式下的寿命都大于的概率,在只考虑工程失效模式情况下的表达式为:

(15)
其中:为工程失效模式数。对于3.1节中LIPS-200的三阶段任务,能够据此进行分阶段的工作可靠性评估,例如完成第二阶段任务的可靠性为:

3.3 可靠性评估的进一步简化
在工程实际应用中,除了前面叙述的由全部失效模式到工程失效模式的简化外,对单工作模式离子推力器还可以进行以下三方面的简化:
1)基于相似磨损机制的威布尔参数简化
就离子推力器的某一工程失效模式而言,其威布尔寿命分布函数中的时间标度因子主要取决于失效特征参数的变化速率,也就是相应磨损应力的大小;而形状因子主要取决于磨损机制,也就是磨损应力的类型,如电荷交换离子溅射或放电室一次离子溅射。由此可见,对于同一失效模式,不同工作模式下其磨损应力大小不同,但磨损应力类型相同(即=);例如FM2和FM5的磨损应力均为交换电荷离子溅射腐蚀,≈。因此当LIPS-200只有FM1、FM2和FM5三种工程失效模式时,式(15)就简化为:
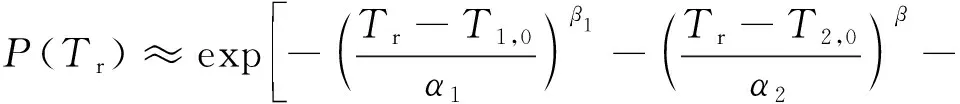
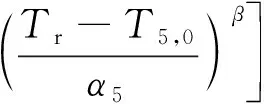
(16)
==
(17)
2)基于均匀磨损过程的威布尔参数简化
如果工程失效模式对应的磨损率是时间均匀的(如FM1失效模式),这种情况下=1,式(16)继续简化为:

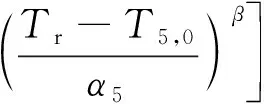
(18)
3)基于关键失效模式的简化
针对具体工程任务,如果除了关键失效模式外,其他工程失效模式的寿命裕度都大于1.5,则可靠性评估仅考虑关键失效模式即可。对LIPS-200来说关键失效模式为FM2,可靠性评估进一步简化为:
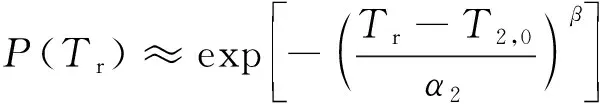
(19)
应用式(13)中的分布函数,可以得到推力器在3.1节所述任务中三个阶段工作的可靠性分别为1.0、1.0和0.9994。
4 结 论
针对LIPS-200产品成熟度提升和多型号应用中的工作寿命及可靠性定量评估需求,通过问题梳理、关系分析、方法论证和举例说明,获得的单工作模式离子推力器寿命及可靠性定量评估的主要结果包括:
1)离子推力器的寿命及可靠性定量评估的技术困难主要来源于失效模式种类多、各失效磨损模型的输入参数多、以及磨损模型与输入参数不确定度之间的相互耦合;
2)解决技术难题的主要方法为通过分析模型、验证试验和数值模型之间的不断迭代实现各失效模式对应磨损模型的精确化,通过试验数据和精确化磨损模型抽样计算数据的样本检验获得准确的寿命概率分布参数;
3)应用各失效模式对应寿命的三参数威布尔分布函数,就可以进行针对工程应用的离子推力器寿命及可靠性定量评估,包括阶段性中期评估和全寿命末期评估;
4)实际工作中可进行合理的简化,一般简化顺序为首先排除非工程失效模式,然后重点选取敏感度和权重较高的输入参数进行抽样计算,最后适度应用各类失效磨损机制及其寿命分布参数的特点。
本文给出了单工作模式离子推力器工作寿命及可靠性定量评估的通用方法,主要针对LIPS-200离子推力器的FM2失效模式及其磨损模型进行了初步的解析计算,后续将针对复杂失效模式及其数值模型进行更深入的研究。此外,如何将本文所述方法拓展应用于双工作模式甚至多工作模式离子推力器则成为新的技术难题。

