微型燃料电池内传输数据模型建立及实验研究

孙 刚，王晓辉

(1.中广核风电有限公司，北京 100143；2.华北电力大学控制与计算机工程学院，河北保定 071003)

随着微电子设备种类与功能的日益增多，微型燃料电池的供电性能备受关注[1]。在众多类型的微电池中，无膜微流体燃料电池利用层流流动的原理将燃料和氧化剂进行隔离，取代了带有离子交换膜的传统结构，从而有效降低了电池的生产成本，得到了广泛的应用[2]。多数微流体燃料电池的阳极是平面的，在这种结构形式下，随着电池内部化学反应的进行，阳极表面会产生高密度燃料边界层，从而减缓燃料传输速度，对电池的整体供电性能造成较大影响[3]。为了解决这一问题，必须对燃料传输进行强化，主要方法包括增大燃料流量、优化微通道截面高宽比、改变电极或微通道结构形式等，最终目的是促进阳极表面对流的快速流动[4]。其中，通过浸没微射流的形式将部分燃料按既定方向输送至阳极表面，能够在不改变阳极有效作用面积的条件下实现燃料传质的强化，进而使电池的性能得以提高[5]。为了明确浸没微射流方法的效用机制及各种几何参数与电池性能的具体关系，本文对空气自流动微流体燃料电池进行了研究，以电池内部化学反应、物质传输、内部流体活动为主体构建了电池工作的三维数学模型，对多种强化方式及结构几何参数的改变与电池性能变化的关系进行了量化分析。

1 模型构建

1.1 物理结构

浸没微射流空气自流动式微流体燃料电池的物理结构如图1 所示。电池的燃料为甲酸钠-氢氧化钠钾溶液，从主流道下部流入，电解液为氢氧化钾溶液，从主流道上部流入，二者在流道中平行流动。小部分燃料被送入电池中心线上的毛细管，毛细管的微射流出口微孔开在阳极侧。浸没微射流对阳极表面产生的高密度燃料层进行冲击破坏，同时不断输送新的燃料，由此实现对燃料传质的增强，使电池的整体性能得以提升。通常采用主流道出口的Re数来描述电池内部流体的流动状态，其表达式为[6]：

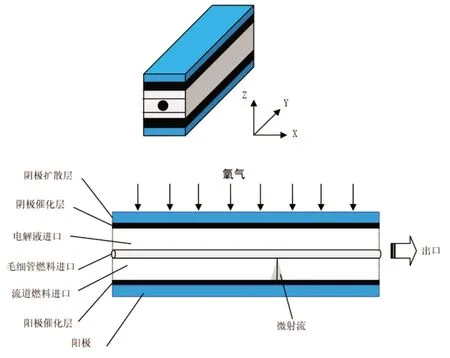
图1 微流体燃料电池的物理结构

式中：μ、ρ、u分别为燃料和电解液流体在主流道出口的平均黏度、密度和平均流速；d为主流道横截面的当量直径。由式(1)可求得Re数约为2.6，所以电池内部流体可视作以层流的形式进行流动。

1.2 建立数学模型

依据空气自流动微流体燃料电池的工作特性，本文基于如下假设建立电池工作的数学模型：(1)忽略电池内部流体的重力且其层流流动处于不可压缩状态；(2)电池处于稳定恒温的共组环境；(3)阴极内的氧气以纯扩散的形式进行输送；(4)扩散渗透至阴极中的燃料全部被氧化[7]。

(1)流体的流动

电池主流道中燃料和电解液流体的流动可通过连续性方程与N-S 方程求得：

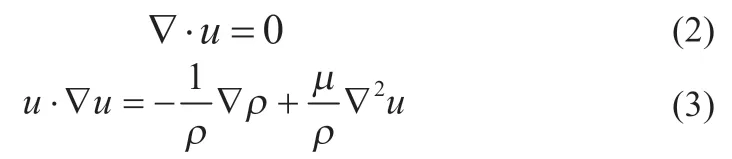
流体在电池两极多孔催化层中的流动方程为：

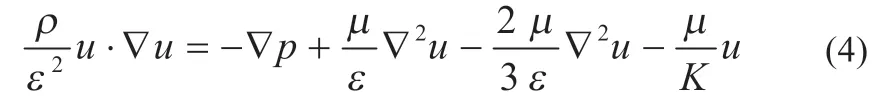
电池工作过程中燃料的黏度会随其浓度的变化而改变，具体改变量为：

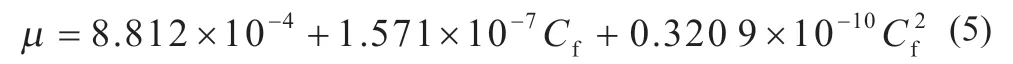
式中：p为流体压力；ε 为多孔结构物体的孔隙率；K为其渗透率；Cf为局部位置处燃料的浓度。

(2)物质的输送

电池内部燃料对流-扩散传输过程表达式为：

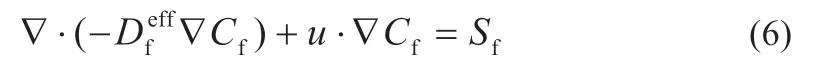
氧气在阴极侧的传输过程可利用Maxwell-Stefan 方程的形式进行表达，即：

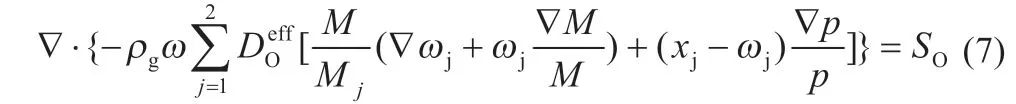
式中：SO为反应源项，其仅存在于阴极催化层中，在其它各处的值都是0。

多孔物体内部有效扩散系数可通过Bruggeman 关系式进行修正，具体方式为：

(3)电池内的电荷守恒

在电池的主流道中，各种离子的电势遵守电荷守恒定律，即[8]：

由此多孔物体内部电极与离子的电势满足以下两个方程：

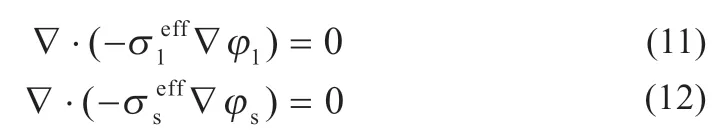
式中：σl、σs分别为电池内的电解液与电池电极的导电率；φ1、φs分别代表离子和电极的电势；上标eff 表示实际有效值。

(4)电池内的化学反应

燃料在电池的阳极催化层中会产生电化学氧化反应，反应进行速度的表达式为：

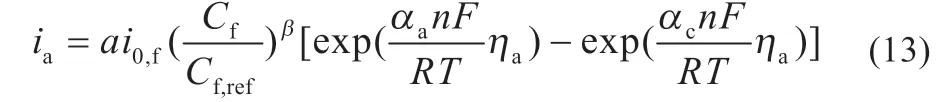
氧气在电池的阴极催化层中产生电化学还原反应，反应进行速度的表达式为：

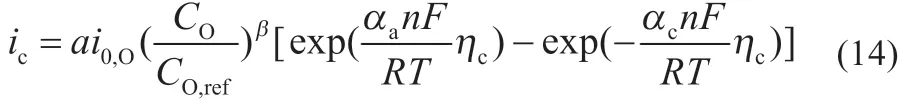
式中：a为活化比表面积；i0,O、i0,f分别为电池阴阳两极所产生交换电流的密度；CO、Cf分别为电池内部某处氧气与燃料的浓度；CO,ref、Cf,ref分别为氧气与燃料的参考浓度；β 为反应级数；ac、aa分别为电池阴阳两极的电荷传递系数；R为气体常数；n为电化学反应过程中发生转移的电子总数；ηc、ηa分别为电池阴阳两极的过电位。

微通道横截面尺寸为20 mm×2.5 mm×1.5 mm，毛细管内径din为0.3 mm，外径dout为0.5 mm，微射流孔直径dpore为70 μm，电池两极的催化层厚度δCL均为20 μm，阳极集电体以及阴极扩散层的厚度均为280 μm。所构建模型涉及的参数和电池工作状态参数如表1。

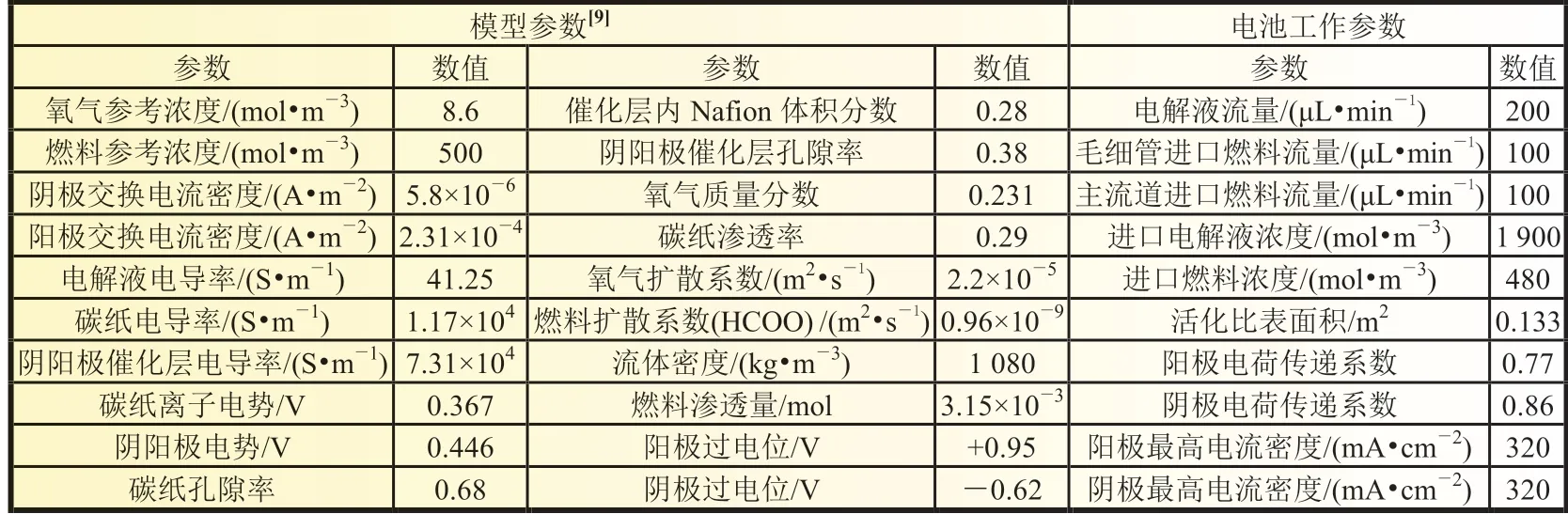
表1 参数汇总

(5)模型的边界条件

假设在微射流毛细管与主流道的进口处燃料与电解液流体的流量是固定的，同时其出口处压力值与大气压相等且为压力边界条件，模型中其它避免的边界条件均为速度无滑移状态。假设电池内燃料和电解液流体的浓度是固定的，二者流出处为出流边界条件。电池阴极催化层顶部无燃料，气体质量分数与氧气相同，其它位置为无渗透发生的边界条件。假设阳极电压为0 V，阴极电压与电池的输出电压相等，电池内部所有位置电势连续，其它均避免处于绝缘状态。

1.3 网格数量无关性

为了确定网格数量是否能够对模型计算结果产生影响，分别在625 468、772 697、903 185 网格总数的条件下进行模型训练计算，得到极化曲线如图2 所示。图2 中的3 条曲线完全重合，可见网格数量不会影响模型的计算结果。本文在实验过程中将网格数量设定为625 468。

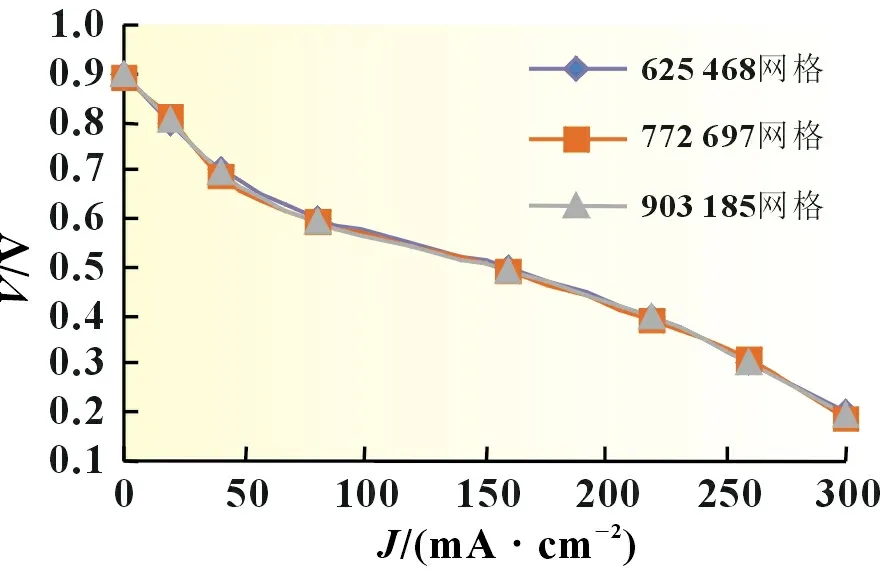
图2 不同网格数量下的极化曲线

1.4 模型测试

为了验证所构建模型的合理性和有效性，本文基于Zhou团队[10]的浸没微射流电池和实验工况进行仿真计算。实验用电池为浸没微射流空气自呼吸无膜微流体燃料电池，燃料经阴阳两极之间设置的毛细管上的射流孔喷射至阳极表面。电池阳极由亲水性碳纸和Pd/Nafion 催化层组成，电池阴极由疏水性碳纸、整平层和Pt/C 催化层组成。实验过程中，向阳极流道和毛细管内以200 mL/min 流量注入经过除氧处理的甲酸钠与氢氧化钾混合溶液，向阴极流道内以相同流量注入氢氧化钾溶液，自注入燃料和电解液开始全程测量电池输出电压。将得到的数值结果与文献[10]的实验数据进行对比，结果如图3 所示。由图3 可见，通过仿真所得到的功率密度曲线和极化曲线与利用真实实验数据所绘制的曲线具有很高的吻合度。同时，按照文献[10]中的计算方法可得泵的功率为1.12 mW，而模型的峰值功率为6.23 mW，由此可认定泵的功率可以忽略不计。

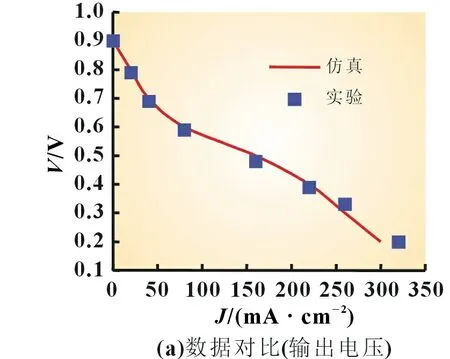
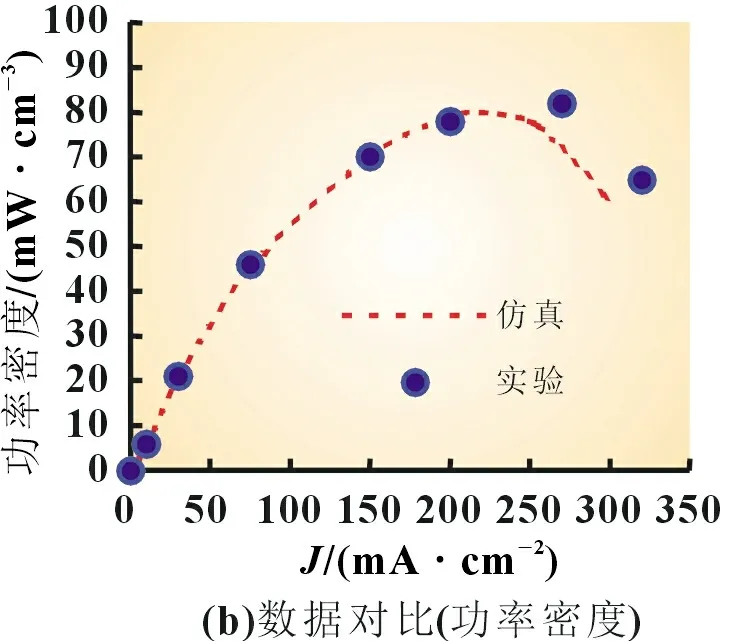
图3 模型仿真计算与真实实验数据对比结果

2 结果与分析

本次研究过程中分别在不同射流孔位置、不同射流孔数量以及不同射流孔直径的条件下对电池内部物质传输及电化学反应的持续过程进行了模拟，以量化的方式分析了不同几何结构状态对电池内部传质和供电性能的实际影响。

2.1 不同射流孔位置

将射流孔位置分别设定在L为5、10 和15 mm 的位置，统计电池的输出电压与功率变化关系。统计可知，在电流密度较高的条件下，射流孔位置能够对电池性能产生更为明显的影响，其原因在于电池阳极侧的电化学反应进行的速度较其它位置处更快，高密度燃料边界层的形成对电池的性能产生了关键性的影响。微射流结构使燃料输送得到增强，不断向高密度燃料边界层补充燃料，有效提升了电池性能。当射流孔所在位置由L=5 mm 下移至L=10 mm 处时，电池的功率密度峰值也由80.9 mW/cm3升高到了85.9 mW/cm3；而当射流孔位于L=15 mm 处时，电池性能只是稍有提升，原因是在此处燃料高密度边界层已累积到一定的厚度，对阳极性能已经产生了较大的限制，同时，微射流的作用区域十分接近出口，冲击范围较小，因而微射流在阳极表面的作用面积有所减小，电池性能仅获得小幅提升。

电池输出电压为0.4 V 时，其内部主流道中燃料在不同位置的浓度、射流中心截面处流体各方向矢量速度以及阳极表面燃料的浓度如图4 所示。由图4(a)可见，射流孔位于L=5 mm 处，高密度燃料层处于较薄的状态，此时燃料传输尚不能影响附近位置的反应速率，所以通过微射流增强燃料传输的效果并不显著，同时后段阳极表面上生成的高密度燃料层尚未被冲击破坏，因此微射流只能小幅提高电池的性能。射流孔下移至L=10 mm 处后，主流道前段所形成的高密度燃料层已经累积到一定的厚度，燃料微射流对其的冲击和补充持续进行，使局部燃料的输送和后端高密度燃料层内部的传质得到加强，加快了阳极电化学反应的进行速度，从而使电池性能得以提高。而当射流孔继续下移至L=15 mm 处时，由于前段高密度燃料层已经达到了一定的厚度，对阳极性能产生了较大的限制，且微射流出口与作用区域距离较近，流体流动速度不高，因此产生的影响并不大，理论上会降低电池的性能，但本次研究的模拟结果显示，电池性能提到了小幅提升，为了分析其中的原因，对微射流中心截面流体的流动情况进行了研究。浸没微射流与阳极碰撞后受到反向作用力，反弹过程中引射了一部分电解液使燃料被稀释，从而影响了后段阳极性能的提升。在射流孔位于L=15 mm 处时，燃料被稀释后产生的影响并不大，所以阳极表面燃料的浓度得以变大，如图4(b)所示。后续的研究结果表明，继续下移射流孔使其更加接近出口位置，电池的性能会随之降低，这是因为得到强化的燃料传输的作用面积变小了。

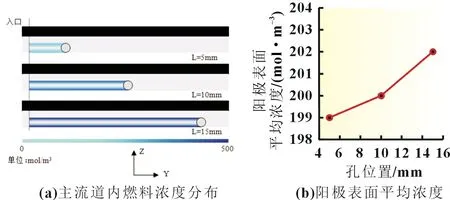
图4 射流孔位置不同时燃料参数的变化

2.2 均匀分布的不同射流孔数量

研究不同射流孔数量条件下燃料传输以及电池性能的变化。设置1 个射流孔时，其位置为L1=10 mm；设置2 个射流孔时，其位置分别为L1=6.7 mm，L2=13.3 mm；设置3 个射流孔时，其位置分别为L1=5 mm，L2=10 mm，L3=15 mm。由图5 可见，射流孔数量增多，出口处流体的流速随之降低，这是分流效应所产生的结果。对电池性能与射流孔数量的关系进行统计，可知随着射流孔数量的增加电池性能先提升后降低，设置2 个射流孔时，虽然流体在出口处的流速降低，但微射流仍能一定速度碰撞阳极表面，对高密度燃料层形成冲击并进行燃料补充，阳极侧的电化学反应速度仍能得到提高，同时，燃料微射流的作用面积也有所扩大，进而使电池性能获得提升。在设置2 个射流孔的情况下电池功率密度峰值为94.8 mW/cm3，相较于1 个射流孔提高了约10%。但是，在设置3 个射流孔的情况下电池性能较2 个射流孔有所降低，燃料传输限制作用十分明显，其原因在于射流孔数量达到3 个后出口处流体流速已经低到一定数值，微射流也已无法碰撞到阳极表面，未对燃料传输发挥足够的强化作用。

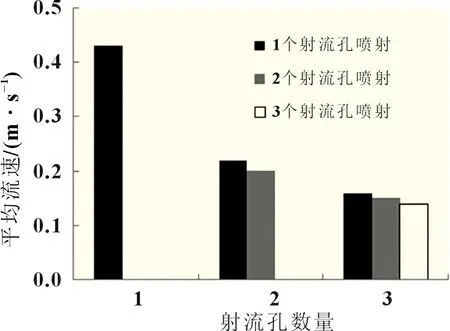
图5 射流孔数量与平均流速的关系

2.3 射流孔直径

不同射流孔直径条件下燃料传输以及电池性能的变化如图6 所示。设置1 个射流孔，其位置为L=10 mm。电池输出电压为0.4 V 的条件下电池阳极表面燃料浓度结构如图6(a)所示，此时电池阳极表面微射流冲击区域浓度较高，说明燃料传质已得到微射流的强化。扩大射流孔直径后，微射流冲击区域的面积变小，阳极表面燃料的浓度随之降低，这与图6(b)中电池性能的改变形式基本吻合，其原因在于射流孔直径增大后射流的流速有所降低，因而弱化了对流传输的作用，未达阳极表面已停止流动。所以，适当减小射流孔的直径能够有效增强对流传输的作用，使燃料传输得到较大幅度的增强。

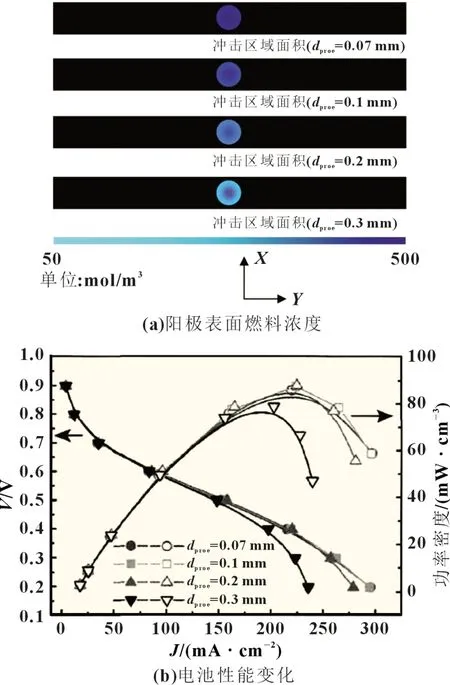
图6 射流孔直径不同时电池性能变化

3 结论

为了丰富浸没微射流空气自流动微流体燃料电池性能提升方式，本文构建了该类电池内部流体输送与电化学反应的三维数学模型，对微射流几何状态参数与燃料传输增强和电池性能提升进行了量化，得到以下几点结论：将射流孔设置在电池中间部位，能够对高密度燃料层形成冲击作用并持续进行燃料补充，使燃料输送得以强化，有效提升电池性能；将射流孔数量由1 个增加至2 个，微射流作用面积变大，电池性能与燃料输送均得以强化。当射流孔数量增加到3 个时，微射流流速较低，无法到达阳极表面，电池性能也有所降低；扩大射流孔直径会使射流速度大幅降低，从而弱化了对流传输的作用，降低了电池的性能。