基于填充曲线和相邻像素比特置乱的图像加密方法

牛 莹 张勋才

①(郑州轻工业大学建筑环境工程学院 郑州 450002)

②(郑州轻工业大学电气信息工程学院 郑州 450002)

1 引言

图像加密技术广泛应用于国家安全、医学成像、隐私信息保护等领域。图像因其像素间相关性高、数据量大等固有特征，传统的加密技术如数据加密标准和高级加密标准等已不能满足图像加密的需求。近年来，人们提出了许多新的图像加密方案，如椭圆曲线方法、希尔加密、DNA加密、混沌加密等[1]。

由于混沌系统具有随机性、不确定性和初始条件敏感性等特点，在图像的编码、解码、加密和隐藏等方面有着巨大的应用前景[2]。1998年，Fridrich[3]提出了一种基于混沌的图像加密体系结构，包括混淆与扩散两个阶段。混淆和扩散是隐藏高冗余和强相关性的两种主要技术。Li等人[4]利用1维混沌序列的随机性对图像的像素位置进行置乱，实现图像加密。1维混沌系统具有效率高、简单等优点被广泛应用，但因其密钥空间小、轨道简单，容易受到攻击[5,6]。Hua等人[7]提出一种2维逻辑调整正弦映射，并应用于图像加密。理论上混沌映射具有非周期特征，由于截断和舍入误差的影响，混沌的轨迹在有限精度的设备上运行时，最终会陷入一个周期内[8]。针对这一问题，文献[9]提出扩展精度的方法来延长混沌映射进入一个周期的时间。然而，因为精度不能无限放大，这种效果是有限的。另一种方法是将多个映射通过级联或切换组合在一起[8]。级联和切换都忽略了多个映射之间可能的相互作用，其组合的效果取决于策略的优越性。Zhang[10]提出了一种新的基于提升变换的混沌图像加密算法。该算法不同于传统的排列扩散结构，具有较高的安全性。

虽然越来越多的基于混沌系统的图像加密方案被提出，大多数现有方案容易受差分攻击，关键在于加密方法没有达到强混淆特性[11,12]。混淆阶段对密码学的影响很大，分为像素级和比特级。比特级混淆与基于像素的混淆相比，具有良好的加密效果，因为比特级混淆能修改像素值，而像素级的混淆只改变像素的位置。也有一些基于比特级的图像加密方法被提出[13,14]，加密算法虽有不同，但都是对单一像素点8 bit二进制数置乱，使得一个像素点比特位0和1的比重不变[15]。为提高的加密算法安全级别，很多加密方案开始采用混合加密的想法，使用一个加密系统的优势来抑制另一个系统的缺点，同时保持他们的优势不变。

2018年，Mozaffari等人[16]提出了一种基于遗传算法和平行比特平面分解的加密方法。所提出的加密方法具有用于多个位平面加密的并行处理能力。同年，Wang等人[17]结合1维混沌映射和约瑟夫问题给出了一种图像加密算法，其约瑟夫遍历方法的置乱效果在一定程度上具有一定的规律性[18]。2019 Chai等人[19]提出一种基于混沌和DNA运算的图像加密算法，该算法能够抵抗典型的攻击，如选择明文攻击等，具有较好的安全性。

本文结合超混沌系统、约瑟夫遍历和填充曲线，提出一种具有高安全性、高敏感性的图像加密方法。通过对约瑟夫遍历方法进行改进，让约瑟夫遍历的步长动态更新，并将其他参数链接到明文图像上，该技术用于隐藏数据的统计特性，减少相邻数据之间的相关性，可以使加密图像的置乱效果更加随机有效。此外，该方法在混淆和扩散过程中加入自适应密钥，以抵御与普通图像相关的攻击，并以较少的计算提高安全性。文献[20]也采用了自适应密钥，但是该密钥来自明文图像的总和与平均值，而本方法采用了明文图像的哈希值作为自适应密钥，对明文变化更为敏感。

2 超混沌Qi系统和约瑟夫遍历

2.1 超混沌系统

超混沌系统具有两个及两个以上正的Lyapunov指数，动力学行为比混沌系统更加复杂，难以预测，在保密通信及信息安全等领域具有更高的应用价值。2009年，Qi等人[21]提出了如式(1)的4维超混沌系统

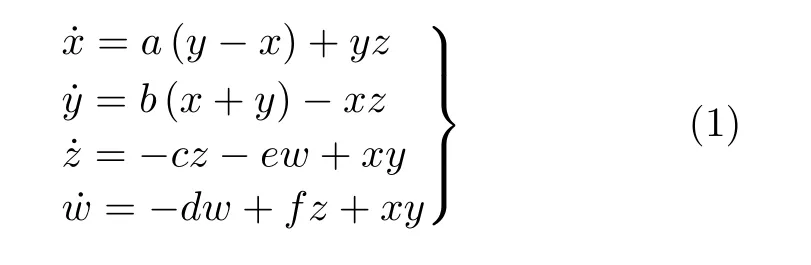
其中，系统的参数为a, b, c, d, e, f均为正数，当a=50, b=24, c=13, d=8, e=33, f=30时，系统式具有两个正的Lyapunov指数，即该混沌系统处于超混沌状态。

使用该超混沌系统作为伪随机数发生器，给定初始值，采用4阶龙格-库塔法进行迭代，可以得到4个超混沌序列{(lxi, lyi, lzi, lwi)| i=1, 2, ···}。该超混沌系统产生的序列符合美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)提供的随机数测试标准，说明该超混沌系统具有伪随机性。

2.2 约瑟夫遍历

约瑟夫遍历是一个经典的数学应用问题：已知n个人（以编号1, 2, ···, n分别表示）围坐在一张圆桌周围。从编号为1的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复，直到所有人全部出列。根据出列的顺序，可以得到一个序列，即约瑟夫序列。将约瑟夫遍历用函数表达，即J= f(n,m)，这里n为元素总数，m为步长，J为约瑟夫序列。为增加约瑟夫的多样性，在原有规则的基础上加入起点r和步长增量k，让约瑟夫遍历的步长保持动态变化，每删除1个元素，使步长进行更新，让m=m+k，k为步长的增量。则约瑟夫函数进一步被拓展为J=f(n, r, m, k)。例如函数J=f(8, 3, 2,1)生成的约瑟夫序列为3, 5, 8, 6, 7, 4, 1, 2。

3 空间填充曲线

由于空间填充曲线具有扫描速度快的特点，在地理研究、多维索引等方面得到了广泛的应用。通过使用填充曲线进行扫描可以对图像进行快速置乱，1条空间填充曲线可以连续访问图像中的所有像素1次，并对每一个像素进行线性排序，将原图像的像素位置打乱并重组得到一幅新的图像。几种常见的填充曲线如图1所示。

4 加密方案

该方案主要包括自适应密钥生成、比特级置乱、像素级置乱和像素扩散4部分。图2给出了加密方案的总体框图。自适应密钥是利用哈希函数，产生与明文图像高度相关的混沌系统的初始值。将这些初始值赋给混沌系统，生成用于加密的随机序列(密钥序列)。结合填充曲线与约瑟夫遍历，采用产生的混沌序列对图像进行混淆和扩散。

图2 加密方案的总体框图

4.1 密钥生成

自适应密钥是提高加密图像抵抗已知明文攻击的有效方法。如文献[22]所述，独立密钥流增加了选择明文攻击的可能性。而由明文图像生成自适应密钥，能达到1次1密的效果。当然，明文图像要高度分散到密钥流中。为此，本文采用明文图像的哈希值来构造混沌系统的初值，图像任何微小的改变，哈希值都会发生巨大的变化，混沌系统的初始值也会随之改变。当然利用不同的系统参数和初始值决定混沌序列密码复杂度的优劣，文献[23]表明，在混沌区间内选择合适的参数，能使产生的混沌序列的自相关特性冲激响应函数，互相关特性接近白噪声。因此，本文对自适应密钥进行处理，控制其落入混沌区间内

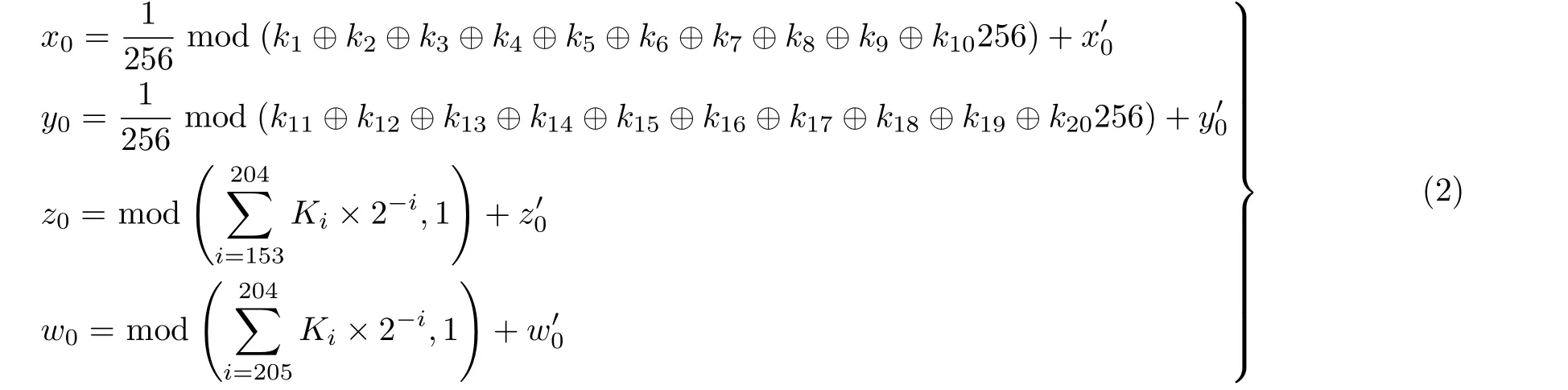
4.2 像素置乱

对于像素置乱，使用填充曲线置乱像素位置十分方便，但是部分填充曲线也存在一定的缺陷，如图1(a)、图1(b)和图1(c)所示的填充曲线，若扫描的次数过少，则打破相邻像素间相关性的能力较差。为此，本文提出一种新的填充曲线，通过V字型从外围到内部再到外围进行扫描，它可以访问2维空间中的每一个点。对于连续3个以上的像素点从不保持相同的方向，避免局部的置乱。采用V型曲线连续扫描两次，原相邻像素再次相邻的概率接近于0。图3(a)为V型曲线的示意图。

图1 常见的填充曲线

如图3(a)所示，在8×8的网格中，从左上角开始，按照V型曲线路径，对图3(a)的数据矩阵进行扫描，得到图3(b)所示的数据矩阵。对图3(b)的数据矩阵再次扫描得到图3(c)所示的数据矩阵。

图3 V型填充曲线的置乱示意图

4.3 相邻像素比特置乱

像素级置乱破坏了相邻像素之间的相关性，但不能改变像素值，因此，无法有效地抵抗统计学攻击。而比特级置乱在置换过程中会影响像素值和像素中比特的位置，因此越来越多的学者引入了比特级置乱方案。当然，如果所有像素的比特置乱都遵循相同的结构，那么就可能导致统计攻击。为实现高效的置乱，本文提出一种相邻像素间比特置乱的方法，该方法将约瑟夫遍历与混沌序列相结合，针对相邻像素的约瑟夫遍历，均采用不同的起点和动态步长，确保在遍历过程中步长自动更新。

综合置乱效率和效果，这里设定每4个相邻像素为一组，并转换成二进制形式，对其进行约瑟夫遍历。为进一步增强置乱的效果，规定下一组的第1个像素为上一组(已进行约瑟夫遍历)的最后一个像素，充分利用了全局置乱后相邻像素点间的相关性被完全打破的特性，解决单一像素点二进制下置乱所用混沌序列不敏感问题，也间接实现了像素的扩散。

4.4 像素扩散

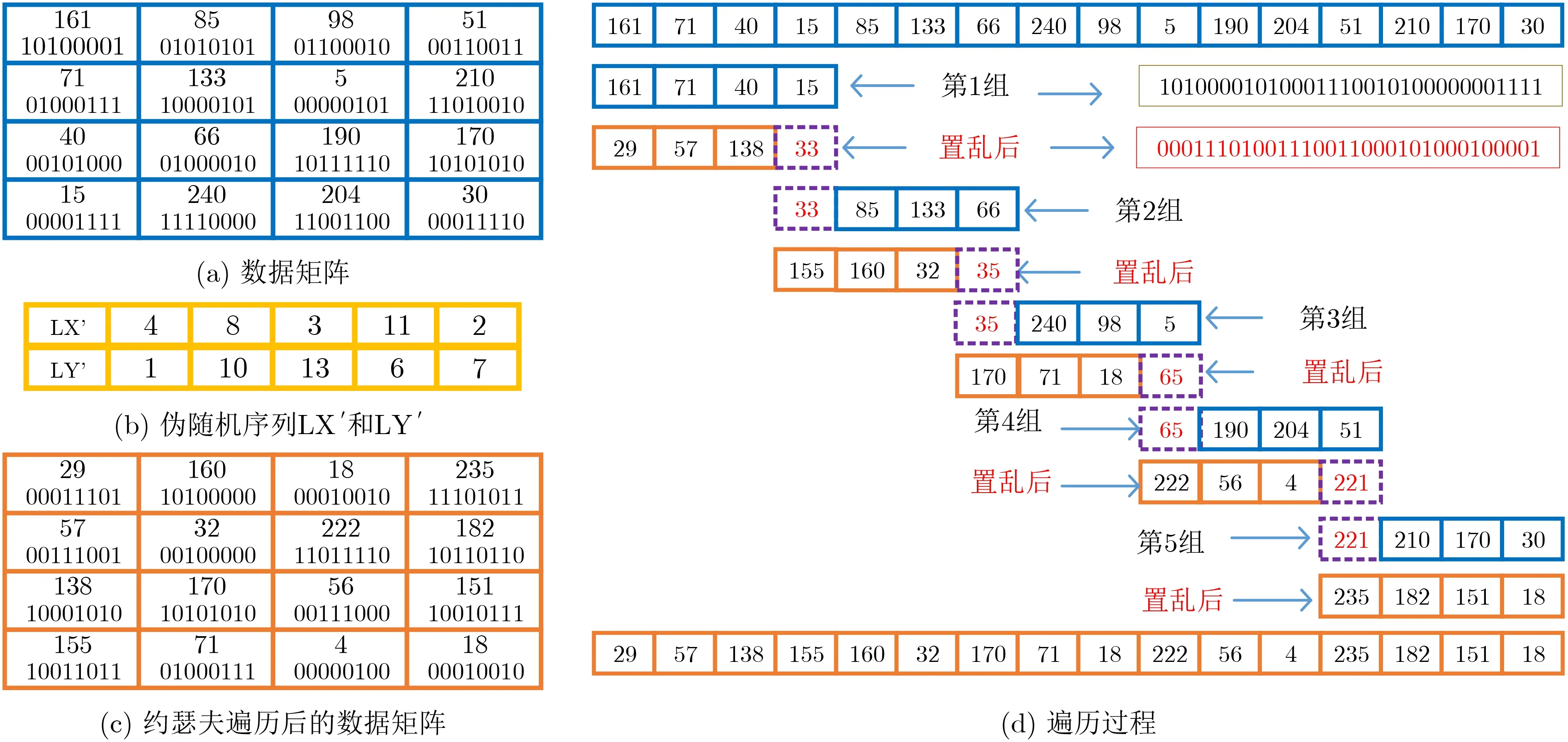
图4 采用约瑟夫置乱的实例

扩散操作使明文的微小变化可以扩散到整个密文，增强了算法对差分和统计攻击的抵抗力。本文结合混沌序列，利用图像的前一个像素值与混沌序列的元素值来共同改变当前的像素值，将少量的明文图像变化传播到整个加密图像。本方法的密钥序列与明文图像高度关联，进一步提高了图像的安全性。扩散过程包括正向扩散和反向扩散。给定混沌初始值，迭代混沌系统产生长度为M×N的两个序列LZ和LW，按照式(4)对序列元素进行处理，并转换成大小为M×N的矩阵形式，记为序列矩阵MZ和MW

其中，i=M, M–1, ···, 1, j=N, N–1, ···, 1。

5 实验结果与安全性分析

5.1 密钥空间分析

5.2 密钥敏感性分析

密钥的高度敏感性是任何好的加密系统的一个重要特征。在解密过程中，加密后的图像即使密钥稍有变化，也无法得到正确的解密图像。为测试本文算法的密钥灵敏度，以Cameraman图像为例，使用改变的密钥来解密密文图像。解密结果如图6所示。原始图像可以用正确的密钥精确地解密。初始参数x0的轻微改变，即使其他密钥保持不变，也无法解密图像。通过以上分析可以看出，本文所提方案对密钥非常敏感。

图6 解密密钥敏感性测试结果

5.3 统计分析

统计能力是指系统抵抗统计攻击的能力。它有两个指标，直方图和相邻像素之间的相关性。

(1) 直方图：直方图是数字图像的重要统计特征，能直观地反映图像中灰度值的分布情况。理想的加密图像应该有一个均匀的直方图。图7(a)是图5(a)中明文图像的对应直方图，图7(b)是图5(b)中密文图像的对应直方图。从中可以看出原始图像的直方图分布不均匀，而加密图像的直方图分布非常均匀。加密图像破坏了原始图像的统计特性。因此，该算法能有效抵抗统计攻击。进一步，通过卡方检验证明其一致性，χ2分布的计算方法如式(7)所示

图5 仿真结果

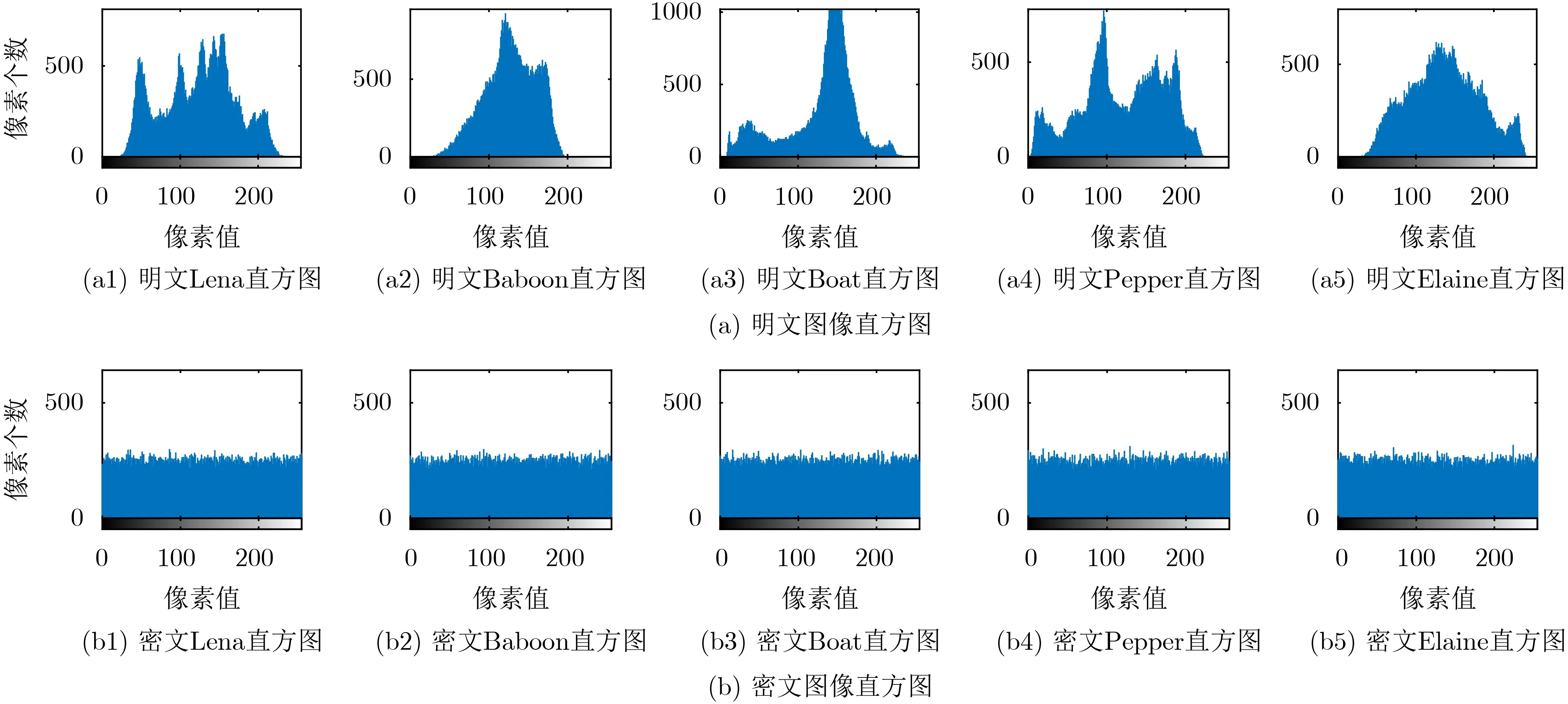
图7 直方图

为计算图像相关性，从原始图像和加密图像中分别选取5000个相邻像素对。计算它们在水平、垂直和对角线方向的相关系数。原始图像和加密图像的相关系数如表2所示。从表2可以看出，加密图像的相邻像素之间的相关性非常小。即3个方向上相邻像素之间的相关性都小于0.01，原始图像的相关系数接近于1。图8也表明，原始图像具有较强的相关性，而密文加密图像的相关性呈现随机分布。

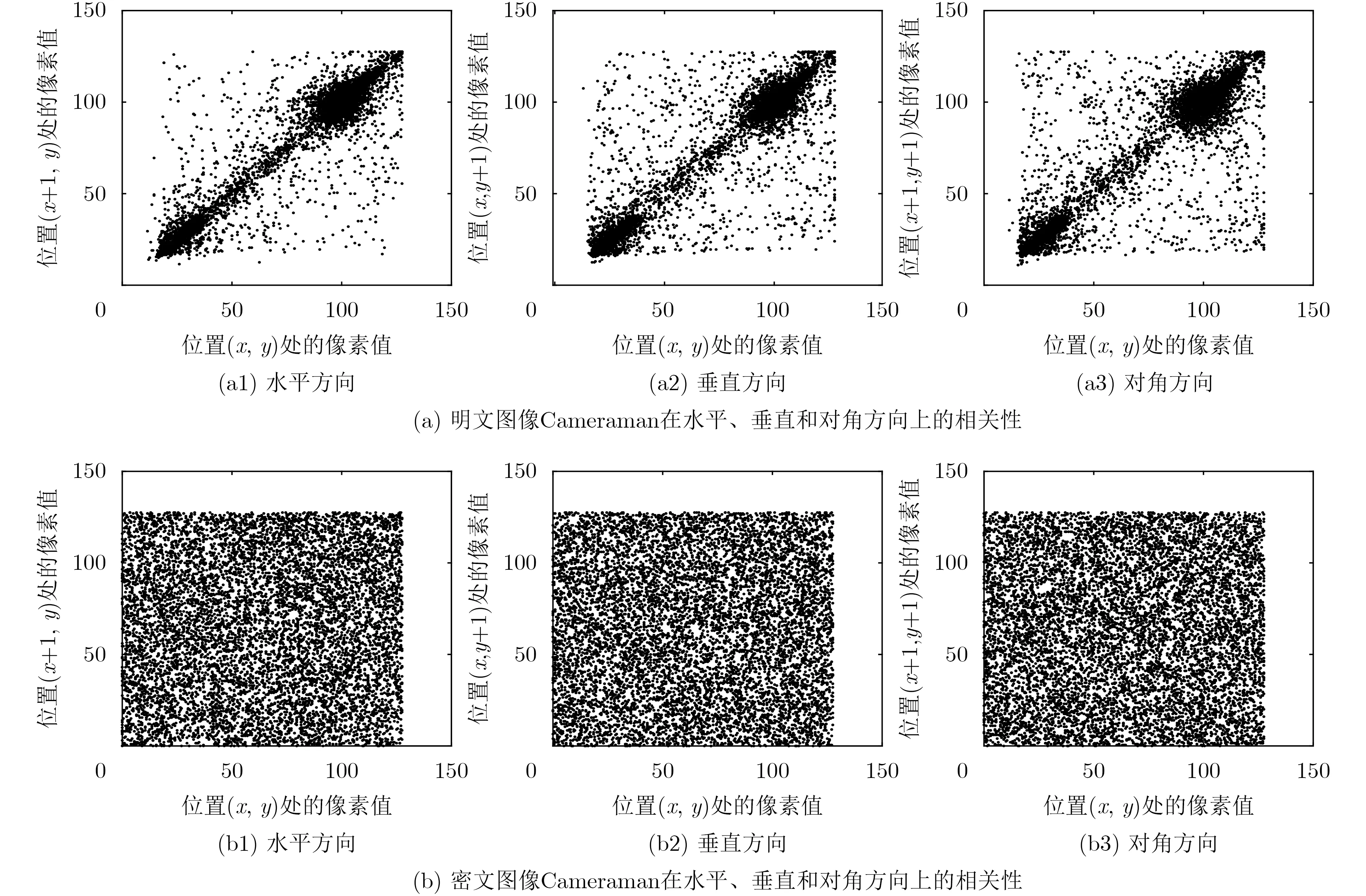
图8 相关性分析

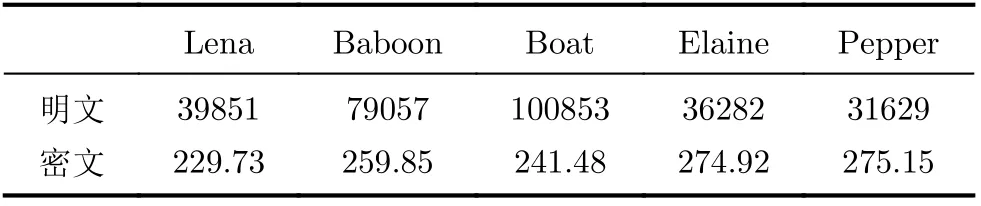
表1 不同图像的密文图像的χ2分布统计

表2 明文图像和密文图像各方向的相关系数

5.4 信息熵

信息熵是衡量图像随机性的重要指标。它能反映像素值的分布。当信息熵很大时，像素值的分布比较均匀。信息熵定义为

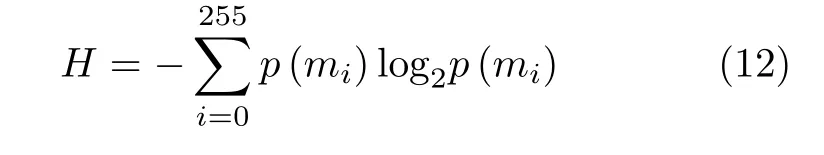
式中，p(mi)表示灰度值mi的概率分布。灰度图像的信息熵越接近于8，图像的随机程度越好。明文图像及密文图像的信息熵如表3所示。该系统产生的密文图像的信息熵最大值为7.9975，接近理想的熵值，这表明该密码系统具有较高的随机性。

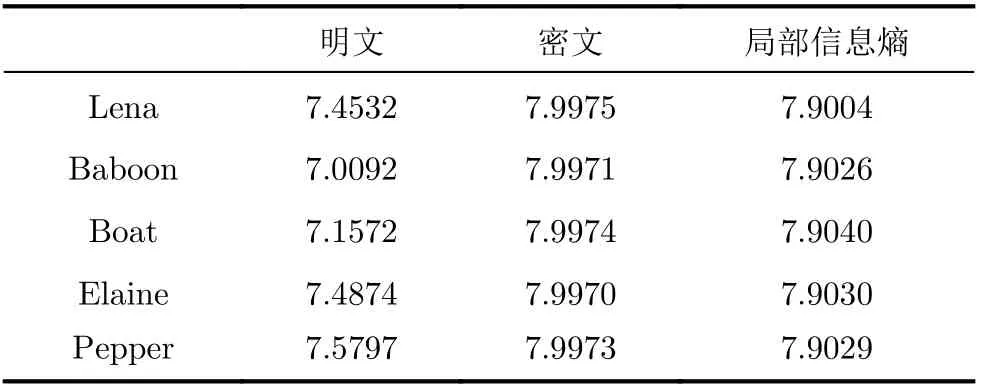
表3 不同图像的信息熵和局部信息熵

5.5 差分攻击分析

差分攻击是将明文图像和加密图像之间的差异建立一种关系来预测原始图像。像素数变化比(Number of Pixels Change Rate, NPCR)和统一的平均变化强度(Unified Average Changing Intensity, UACI)是评估差分攻击的两个重要指标。NPCR反映的是原始图像改变后加密图像中改变像素的个数。NPCR值越大反映其抵抗明文攻击的能力越强。UACI反映的是两个加密图像中对应于原始图像和改变后的原始图像的像素值的平均差值强度。UACI值越大反映其抵抗差分攻击的能力越强。测试图像的NPCR和UACI值如表4所示，均接近理论值。

表4 明文图像发生微小改变时，对应密文图像间的NPCR和UACI的值(%)

5.6 数据丢失攻击分析

在信息传输过程中，当攻击者无法解密加密文本时，通常采用干扰通信的方法来阻止接收方正确解密以达到攻击的目的。其中，裁剪攻击是最常用的方法。本文通过对加密图像Cameraman进行不同程度的裁剪攻击，测试该方法的鲁棒性。实验结果如图9所示。结果表明，本方法能有效地抵御数据丢失的攻击。

图9 数据丢失攻击分析

5.7 抗噪声攻击分析

在图像传输过程中，噪声会对加密后的图像质量产生一定的影响。本文在密文图像中加入不同的椒盐噪声，并用正确的密钥进行解密。给出了加入不同强度噪声后的密文图像，并对其进行解密，结果如图10所示。结果表明，解密后的图像仍然可以被识别。因此，该算法能够抵抗噪声攻击。

图10 遭受噪声攻击的密文图像和对应的解密图像

5.8 对比分析

为方便所提出的方法与已有文献进行比较。取大小为256×256的Lena和Pepper图像进行对比分析，结果分别如表5和表6所示。从结果中可以看出，文献[12]的信息熵值稍高于本文提出的方案，但文献[12]的差分攻击指标略低，其余文献方案的熵值都小于或接近本文方案。文献[11,13,20]均采用了双重置乱模式，文献[11]直接采用混沌序列进行双重置乱，由于截断和舍入误差的影响，混沌系统的轨迹有可能进入一个周期内，降低了其置乱程度。文献[20]的信息熵、NPCR值略低，这和密钥来自明文图像的总和或平均值有关，与明文图像关联性不强。文献[13]的3个评价指标和本文方法接近。由此可以看出，该算法对密钥和明文图像具有较高的敏感性，并能抵抗已知普通和选择普通攻击、遮挡攻击和噪声攻击。因此，本文方法比其他图像加密方案具有更好的性能。

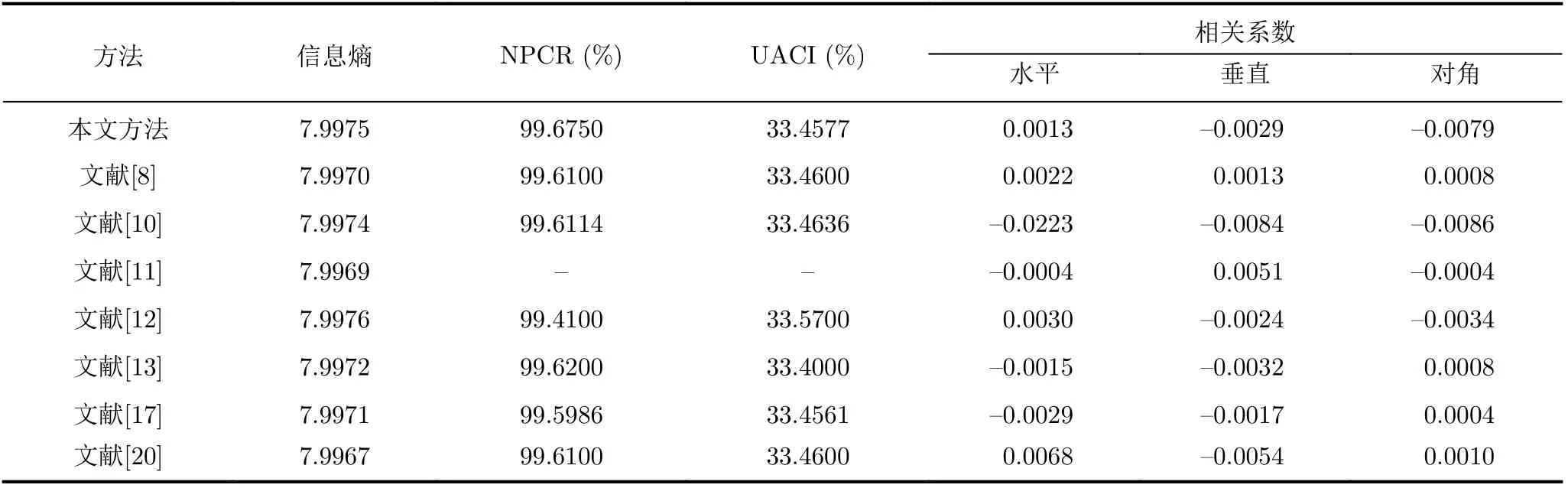
表5 对于大小为256×256的Lena，本方案与其他方法的对比结果

表6 对于大小为256×256的Peppers，本文方案与其他方法的对比结果

6 结论

本文给出一种基于填充曲线和相邻像素置乱的图像加密方法。通过对约瑟夫遍历方法进行改进，并与混沌序列结合实现了比特级置乱，不同的比特组合采用了不同的置乱参数，有效地增强了抗统计攻击的能力。同时，将密钥与明文图像相关联，以克服明文图像相关的统计攻击。利用自适应密钥函数改变每幅明文图像的超混沌系统初始参数，以抵抗已知/选择的明文攻击。实验证明了本文方法的可行性和有效性。