基于自适应多项式拟合的涡流测量校正方法
王 宁, 陈友兴, 杨 凌, 金 永
(中北大学信息与通信工程学院,山西 太原 030051)
0 引 言
在能源、化工、航天等行业中,粘贴或喷镀的非金属涂层厚度对整个产品的工作性能、稳定性和使用安全都发挥着极其重要的作用[1]。如固体火箭发动机的涂层是发动机装药的重要组成部分,太厚或太薄均会影响发动机的正常工作[2];石油工业中的运输管道常在其内表面喷涂非金属涂层防止因腐蚀而发生漏油,过厚或过薄均会造成安全事故[3-6]。因此,在产品使用前或使用过程中,有必要对涂层厚度进行测量,以确保其使用安全。
涡流检测以不需要耦合剂、操作简便、结构简单、实时等优点常用于测量特殊金属基体内表面的涂层厚度[7-8]。但在实际测量过程中,被测基体表面形状和探头与被测基体的距离均会对检测线圈与基体的电磁耦合产生一定的影响,从而造成测量误差大。由于常规误差校正方法中往往采用的高阶多项式、高斯函数等拟合方法复杂化会影响实际检测的效率。因此,研究涡流测厚过程中曲面金属误差校正方法简单化、系统化具有实际工程意义。
文献[9]为了提高金属零件表面绝缘涂镀层厚度测量精度,针对大曲率半径1 125,3 000 mm的铝合金试件为研究对象,采用了9阶多项式、多峰高斯函数等四种复杂函数分别在每一种曲率下对电流信号与提离距离进行标定,通过优化标定方法,减小了测量误差。但该方法在一定程度上增加了测量与计算的工作量。文献[10]通过建立二元三阶多项式的拟合模型,研究了磁感应强度与双层涂层厚度之间的关系。文献[11]针对厚涂层测量精度较低的问题,以曲率半径50~80 mm的不锈钢球面为研究对象,采用了4阶多项式、高斯函数等四种拟合函数分别在每一种曲率下对涡流信号与提离距离进行标定,通过优化标定曲线的方法将测量误差控制在0.09 mm以内。文献[12]为提高曲面试件的涡流测距精度,在数值模拟的基础上,研究了曲率对涡流信号的影响,提出了一种基于涡流信号差值的测距修正方法,提高了曲面测距精度。文献[13]通过建立等效电路模型,得到了测量灵敏度与传感器参数之间的关系,通过优化传感器灵敏度实现了对纳米铜膜厚度的测量。
上述研究分析了涡流曲面测量的影响因素,并针对优化标定方法和提高精度等方向做出了相应贡献。在此基础上,本文从涡流测量值与真实值的关系角度,研究小曲率曲面金属误差校正简单化的方法,分析了曲面曲率半径对涡流信号的影响,在能够满足工程应用0.1 mm测量误差要求下,提出了自适应参数的二阶多项式拟合的校正方法,建立了多项式参数与曲率半径的关系。最后通过实验验证该方法的可行性。
1 曲面涂层测厚原理及影响因素
1.1 管状内表面涂层厚度测量原理
利用涡流提离效应进行涂层厚度测量的原理如图1所示。通过涡流探头到被测基体内表面提离距离x0的大小即可计算出涂层厚度。涡流探头垂直置于被测基体的上方,R为曲率半径,d为被测基体的厚度。在测量曲面涂层厚度时易受到被测基体曲率影响,测量误差会变大。采用涡流探头EU15以及涡流传感器eddyNCDT-3300对其内表面涂层进行检测,选取曲率半径R=25 mm、35 mm、50 mm、70 mm、90 mm的管状试件进行实验验证,如图2所示,提离距离范围0.1~7 mm。涡流信号随曲面曲率半径的变化如图3所示。

图2 检测试件
1.2 曲面曲率半径对涡流信号的影响
图3所示为改变被测基体的曲率半径大小,提离1,3,5,7 mm下的测量值随曲率半径变化的情况。可以看出,在同一提离下,测量值随着曲率半径的增大而减小。图4为提离1,3,5,7 mm下涡流信号随曲率半径变化的测量误差。
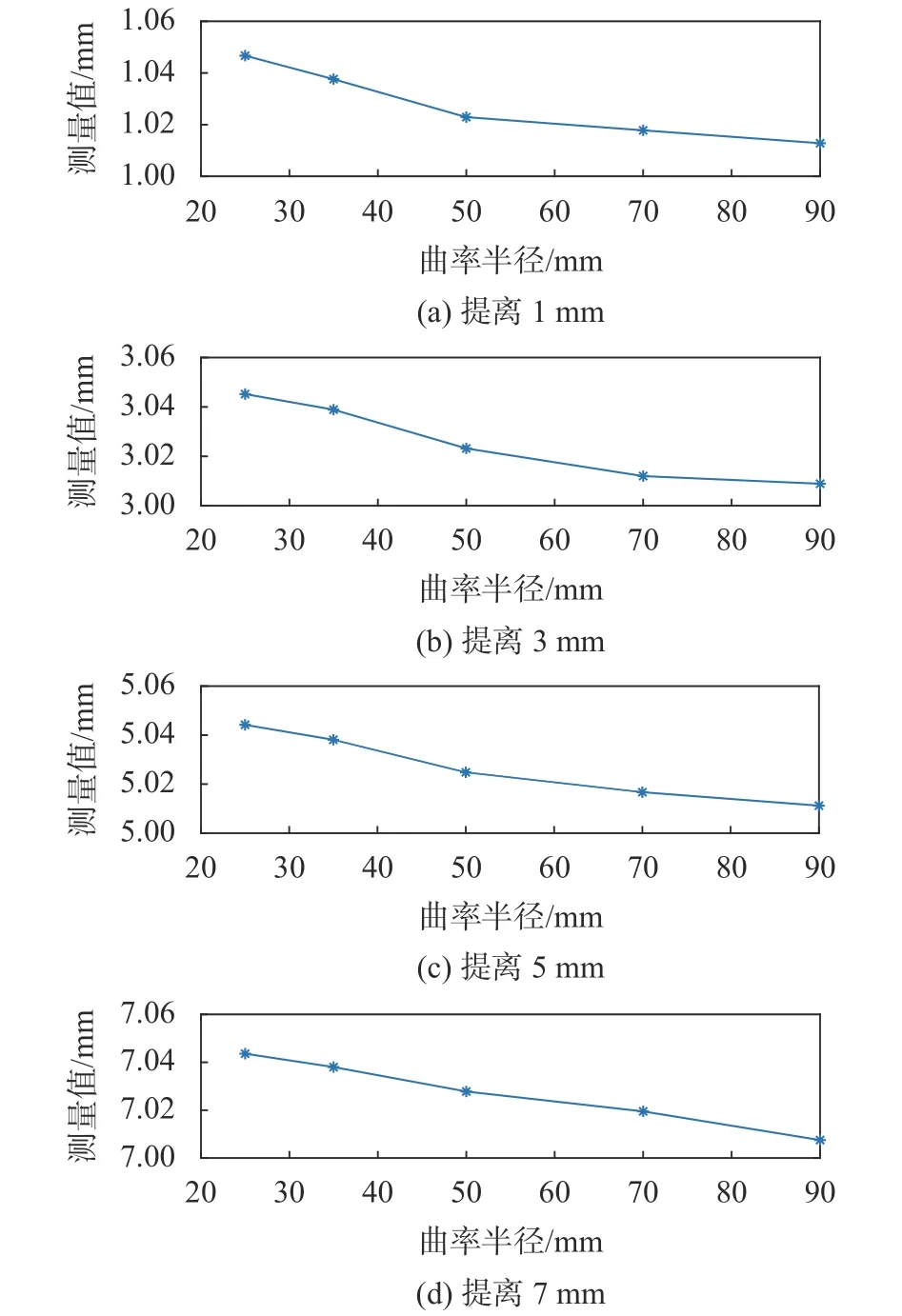
图3 曲率变化对涡流信号的影响

图4 涡流信号随曲率变化的误差
由图4可知,在同一提离下,测量误差随着曲率半径的增大而逐渐减小。在同一曲率半径下,随着提离增大,测量误差也在减小。说明曲率半径、测量值与真实值之间存在一定的关系。
2 多项式拟合校正方法
设拟合多项式为:
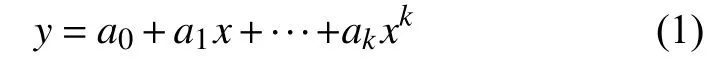
式中:a0、a1、···、ak——待定多项式参数;
k——拟合多项式的最高次数;
x——测量值;
y——真实值。
为更直观表示测量值与真实值的函数关系,测量值在文中具体用表示,真实值用表示。
将式(1)表示为矩阵的形式,可得到:
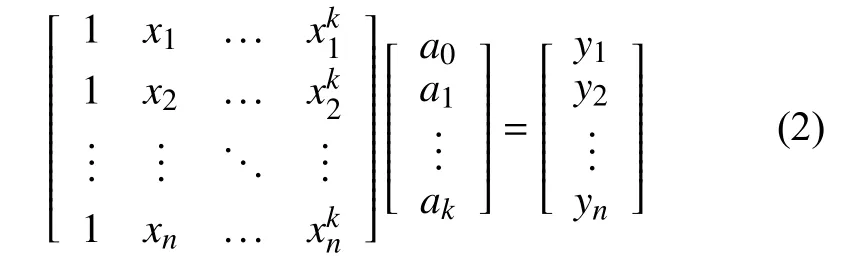
表示为矩阵形式,如下:

系数矩阵A即可由公式(3)计算得出,通过对测量值与真实值进行拟合运算,相比于二阶多项式,四阶、九阶多项式及高斯函数的运算量较大,其多项式参数多且复杂度高。
为更好分析拟合方法的好坏,对四种拟合曲线的拟合指标和方差(SSE)、均方根(RMSE)、确定系数(R-square)进行分析。其中和方差(SSE)越接近0,说明模型选择拟合更好,数据预测也越成功。均方根(RMSE),也叫拟合标准差,表示原始数据相对于拟合曲线的偏离程度,越接近0,误差越小。确定系数(R-square)近似于1时,表明方程的变量对y的解释能力越强,函数模型对数据拟合越好。趋势线最可靠[14]。
通过比较高斯函数、二阶、四阶及九阶多项式的拟合指标,具体对比结果在表1中给出。
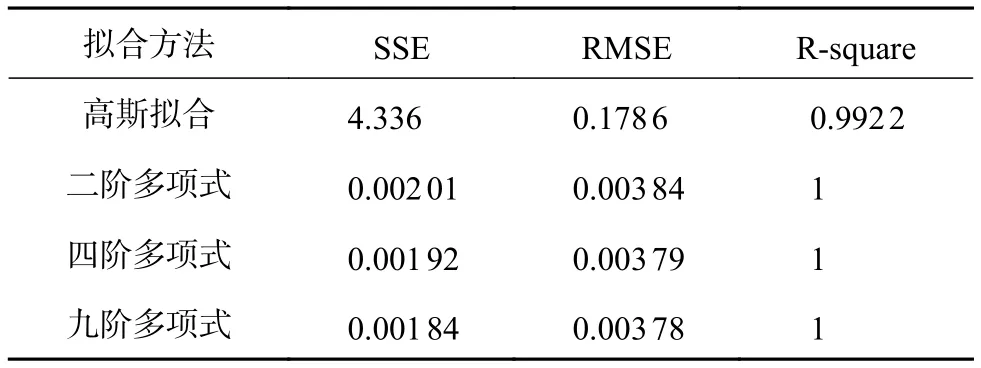
表1 四种拟合方法对比结果
由表1中数据可知,高斯函数拟合指标不理想,而二阶与四阶、九阶多项式相比,各项拟合指标均较接近。进一步分析了4种拟合方法的误差如图5所示,可以看出,高斯函数拟合误差较大,二阶与四阶、九阶的拟合误差相近。
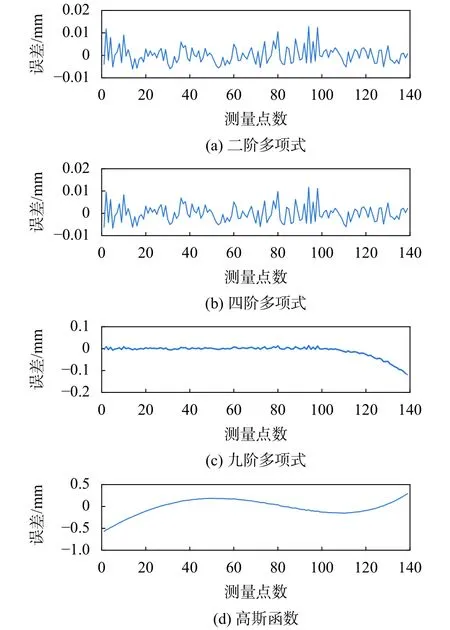
图5 四种拟合方法的误差
综上,为了降低参数复杂度,在满足测量误差的要求下,本文采用二阶多项式的拟合方法,其表达式为:
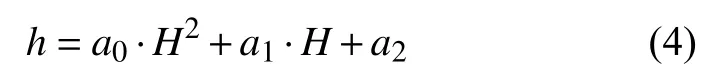
其中h和H分别表示不同曲率半径下的真实值和测量值。
为了验证采用二阶多项式拟合方法的效果,如图6所示,对曲率半径R=25 mm拟合前后的测量误差进行了分析。
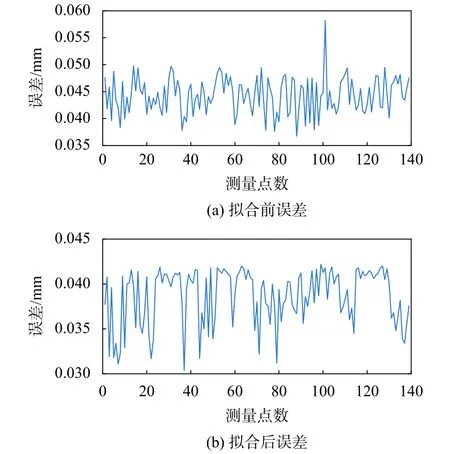
图6 拟合前后误差
从图6可以看出,未拟合时的最大测量误差为0.058 mm,拟合后的最大测量误差为0.042 mm。所以采用二阶多项式拟合比未拟合的误差要小。
由此可得,采用二阶多项式拟合后不仅减小了误差,而且降低了参数复杂度。所以,首先对曲率半径R=25 mm时的测量值与真实值进行拟合,其结果如图7所示。
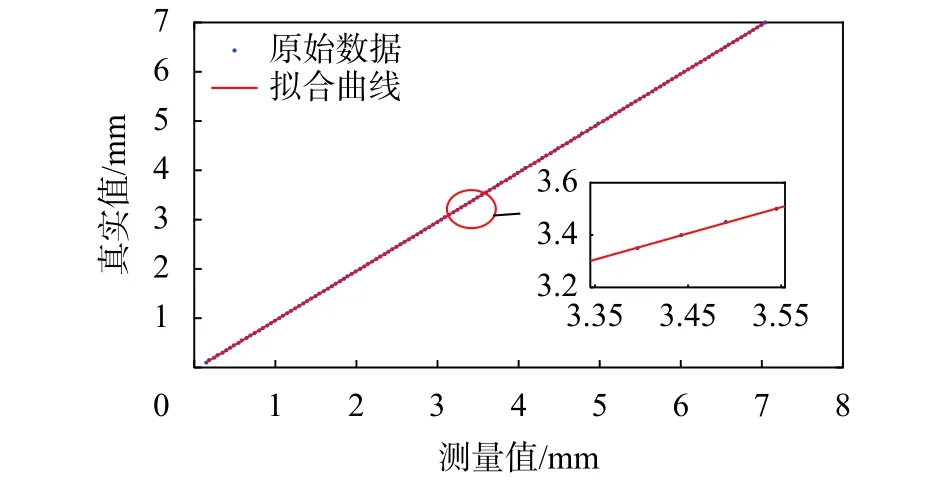
图7 拟合结果
从图7可知,二阶多项式拟合曲线各点几乎分布在曲线上,其拟合曲线与原始数据吻合性很好,偏差最小,同理可得到其余四种曲率半径下的真实值与测量值的拟合曲线。
3 多项式的自适应参数求解
3.1 自适应参数求解
在降低参数复杂度的基础上,进一步将得到的二阶多项式参数系统化,在满足适用性及测量误差的要求下,通过自适应参数求解,建立多项式参数与曲率半径的关系。
在不同系数矩阵A中ak(k=0, 1, 2)的值会随着曲率半径不同而变化,如果按某一个确定的自适应关系f,对于任意半径R,在A中 都有唯一的参数a与之相适应,其自适应关系可表示为:

以本文的5种曲率半径为例,由式(4)分别得到5种曲率半径下的测量值与真实值的表达式。由于多项式参数随曲率半径变化,即参数a0、a1、a2分别为5种曲率半径下对应的5个不同数值。问题转变为分别求参数a0、a1、a2与曲率半径R的函数。
在考虑系数复杂度的情况下,首先以参数a0为因变量,曲率半径为自变量,优先采用二阶多项式对其进行拟合,得到相应的参数a0-曲率半径R拟合函数,由于参数a0与曲率半径R的二阶拟合效果不理想,而采用的三阶拟合效果较好,由此得到了参数a0与曲率半径R的自适应关系:
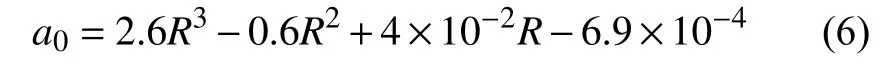
同理分别得到参数a1、a2与半径的自适应关系:
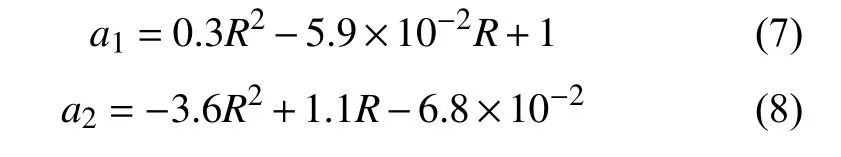
由式(6)~(8)便系统性地建立了各多项式参数与曲率半径的表达式。
将式(6)~(8)代入式(4)即可计算出不同曲率下的实际值。首先计算了曲率半径R=25 mm下的实际值,并与真实值作对比,其结果如图8所示。从图8可以看出,计算的实际值与真实值吻合度很高。
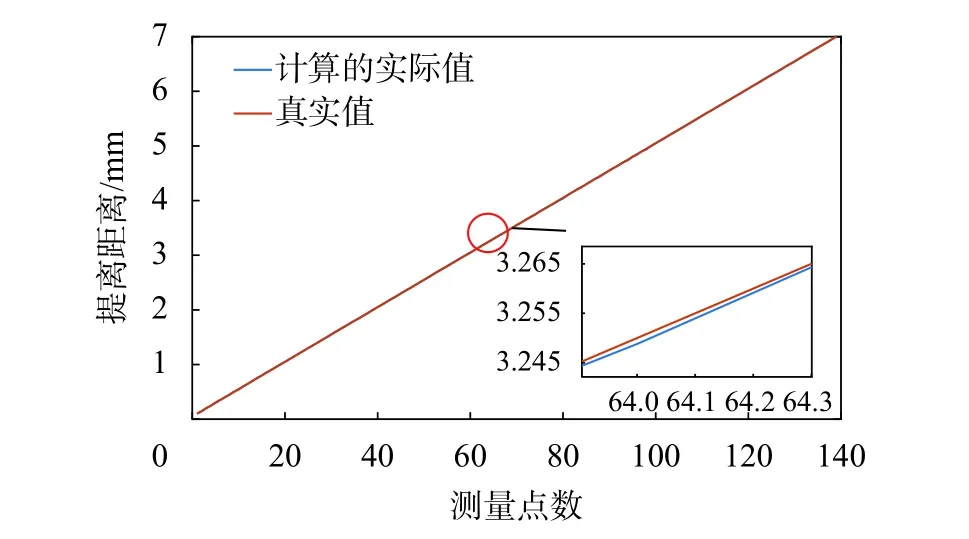
图8 计算的实际值与真实值比较
3.2 实验结果与分析
进一步对比通过该方法计算的不同曲率下的实际值与真实值的误差,结果见图9。由图可得,不同曲率下计算得到的实际值与真实值的最大误差在-0.015~0.015 mm范围内。通过代入后的式(4)不仅可以计算出5种曲率下的实际值,而且计算的实际值与真实值相近,表明该方法具有一定的可行性。
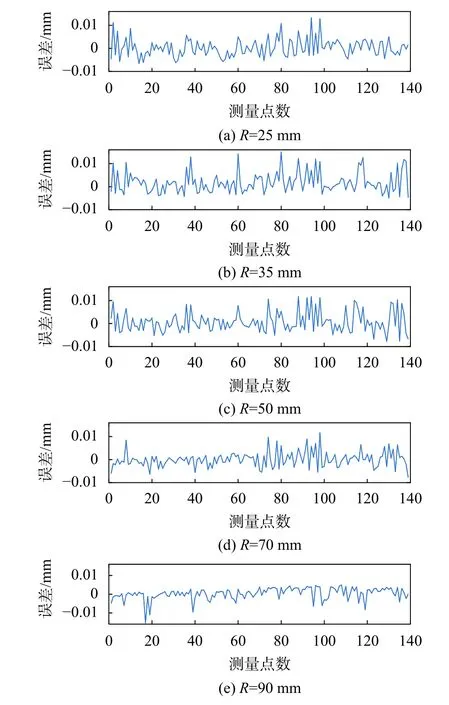
图9 不同曲率下实际值的误差
4 结束语
本文针对管状基体涡流测量中因曲率的影响而导致的测量误差,在常规校正方法中往往采用的高斯函数、高阶多项式等拟合方法复杂化的问题,研究了曲面曲率半径对涡流信号的影响,提出了基于自适应参数的二阶多项式拟合校正方法,通过自适应参数求解,建立了多项式参数与曲率半径的关系。结果表明,相比于直接利用高斯函数、高阶多项式等复杂函数进行校正的传统手段,该方法建立的关系式所计算的实际值与真实值的最大误差在-0.015~0.015 mm范围内,降低了参数复杂度,具有一定的通用性与可行性。
综上所述,通过基于自适应参数的二阶多项式拟合方法建立的函数关系,简化了实际操作流程,使其更方便有效地应用于工程实际中。

