高速列车接触器非线性退化模型建立及寿命预测
刘 广, 陈春俊,, 昝健华, 黄丽霞
(1. 西南交通大学机械工程学院,四川 成都 610031; 2. 轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)
0 引 言
我国高速列车采用引进、消化、吸收、再创新模式,以跨越式迈入世界高铁先进行列,截至2020年底,我国铁路运营里程突破14.63万公里,其中高铁运营里程突破3.79万公里。运营规模逐渐扩大的同时,对高铁列车的运行可靠性提出了更高的要求。电磁接触器作为一种常见的低压控制元件,广泛应用于高速列车牵引电机风机、空气压缩机等电气系统中。随着列车运营里程增加,接触器触点由于电蚀、应力累积等原因产生损耗,性能逐渐退化[1-2]。一旦发生失效,容易引发列车电气系统故障,严重时甚至导致列车意外停运,引发安全事故。由于在线监测接触器电气可靠性的实施成本较高且具有一定的技术难度,为保证接触器的可靠性,目前采用定期更换的方式,即在高速列车运行一定里程后对接触器进行强制更换。经检测,被更换的接触器极少出现失效情况,表明目前的更换规程虽然确保了接触器可靠运行,但是造成了接触器寿命的浪费。因此进行接触器剩余寿命预测研究,有助于科学规划接触器更换规程,对充分利用接触器性能、降低接触器更换成本及保证高速列车可靠运行均具有重要意义。
近年来,国内外学者在开关电器的失效机理以及剩余寿命预测方面进行了大量研究,并取得了丰富的成果。针对电子开关的失效机理,Leung等[1]进行的试验结果表明,触点失效主要原因是电弧对触点的侵蚀。刘帼巾等[2]通过可靠性试验,分析了触点熔焊、接触不良等常见失效模式的失效机理,并提出了改进措施。现行国家标准中也对接触器的失效判据及特征参数进行了规定[3]。针对继电器触点磨损过程中特征参数的变化,翟国富等[4]建立了以超程时间为主变量的预测模型对继电器进行寿命预测。刘建强等[5]仿真分析了触点间隙退化量与超程时间的关系,结合累计燃弧能量与触点侵蚀量的理论公式推导了寿命-超程时间的退化模型,并通过试验数据对模型进行了验证。
由于高速列车、航空航天等领域的电子开关具有高可靠性,难以开展常规试验来获取其寿命数据,需要设计加速试验进行研究。茆诗松[6]总结了常见的加速寿命试验类型及相应的加速模型。吕泽红通过温度应力加速试验,建立了继电器的加速退化模型,并外推出正常温度下的可靠度[7]。
随着统计理论与信号处理技术的发展,考虑到设备退化过程中的时变动态特征及随机性,随机过程被广泛应用于设备退化过程的描述[8-9]。余琼提出了基于随机过程的多失效机理及多退化参数的可靠性评估方法[10]。李奎等[11-12]分别基于Gamma过程和Wiener过程建立退化模型对接触器进行剩余寿命预测。
Wiener过程作为一种重要的随机过程,可描述设备退化过程中的失效产生机理以及动态环境变化产生的随机误差,被广泛应用于设备剩余寿命预测的研究。针对非线性Wiener过程,Si等通过时间-空间变换,求解得到了首达时间分布的解析渐进解以及封闭的设备剩余寿命分布概率[8]。王小林提出基于偏正态随机效应的非线性Wiener过程退化建模方法,并通过EM算法估计了退化模型参数[13]。
由于Wiener过程良好的数学特性,本文从电磁接触器的性能退化机理出发,在加速试验及加速理论的基础上,以超程时间为接触器退化特征,结合非线性Wiener过程建立接触器剩余寿命预测模型,并通过试验数据对预测方法进行验证。
1 失效机理分析及加速试验设计
1.1 接触器失效机理分析
针对某型高速列车冷却风机电磁接触器,该型号电磁接触器主要包括轭铁、反力弹簧、衔铁、线圈、衔铁联动结构、灭弧室、动触点和静触点等结构。该型号接触器的电磁系统结构示意图如图1所示。线圈未通电时,动触点与静触点分离,主回路处于断开状态。线圈通电后产生电磁吸力吸引衔铁带动动触点向下运动,触点闭合,主回路导通。线圈断电后,反力弹簧作用下,衔铁被释放,触点分离,主回路断开。
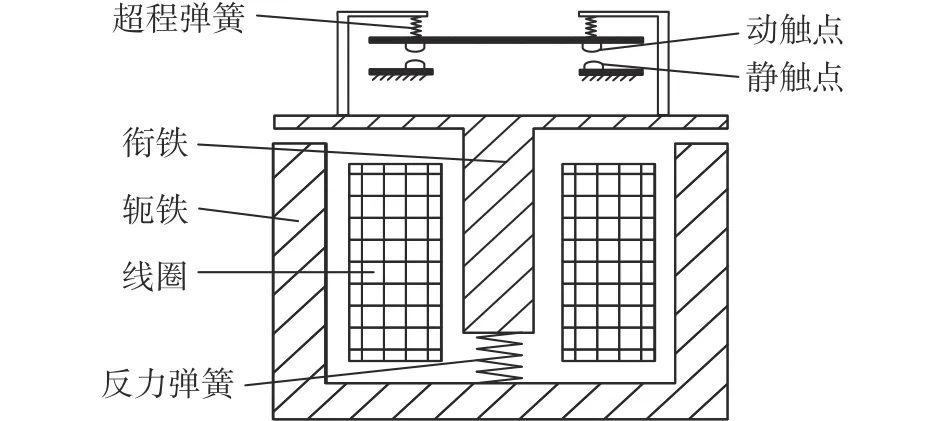
图1 接触器电磁系统结构示意图
大量统计表明,接触器部件中触点是最容易失效的部件,因触点失效导致的接触器失效量占高速列车接触器失效总量一半以上[5]。触点失效主要原因是电弧侵蚀引起触头的电磨损,电磨损是指接触器断开过程中触头间产生电弧、金属液桥等现象,引起触头表面材料发生转移、喷溅和气化,造成触头材料损失,损失量累积最终导致触点发生接触失效[2]。触点退化过程中,接触器的特征参数随之发生变化,其中超程时间对触点磨损量最为敏感[4,10]。
1.2 加速试验研究
由于高速列车冷却风机接触器具有长寿命、高可靠性的特征,故需通过加速试验获取其性能退化数据。触点失效主要原因是电弧侵蚀量的不断累积,文献[12]的研究表明,触点单次动作所受侵蚀量主要受电流影响,可通过提高电流应力增大触点所受的侵蚀量,设计电应力加速试验加快其失效。加速模型中,逆幂律模型[6]作为一种经验模型,广泛应用于电子元件的电应力加速试验研究,其表达式为:

式中:n——加速对象的寿命;
I——电流;
α、β——模型系数,与加速电应力及电子元件的类型相关。
将式(1)两边同时取对数可得线性化模型:

根据式(2)可知,通过试验获取不同电流条件下被试品的寿命,并通过对寿命对数值及电流对数值进行拟合即可确定模型参数 α 、β。电流值选取需按照对数等间距原则:
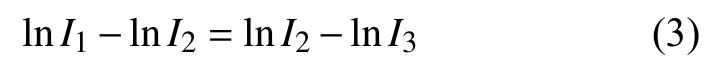
其中,I1、I2、I3分别为3种工况下的电流值。
已知正常工况下,接触器工作电流为25 A,在兼顾试验时长的条件下按照式(3)进行加速试验电流选取,确定电流等级如表1所示。

表1 加速试验电流等级选取
加速退化试验方法主要包括恒定应力加速方法、步进应力加速方法和序进应力加速方法。其中,恒定应力加速方法的理论基础更为成熟,应力施加方式更为简单。因此本文采用恒定应力加速方法,将待测试的12台全新接触器分为3组,每组4台,3组分别对应表1中的3种电流等级。
为进行加速试验共搭建两套试验系统,试验系统实物图如图2所示。试验系统包括冷却风机、电源柜、待测接触器、程控电源、电流传感器、电压传感器、数据采集器、上位计算机。每套试验系统对一台接触器进行试验,待该接触器失效后更换下一台进行试验,同一组的4台样品全部失效后,改变主回路电流应力等级,进行下一种工况的试验,直至3种工况全部试验完为止。

图2 试验系统实物图
接触器串联于主回路,试验过程中,通过程控电源周期性地供电来控制接触器线圈周期性导通,从而实现接触器周期性通断。接触器通断过程中,通过两种不同量程的电流传感器分别采集接触器线圈电流信号和主回路电流信号,所采集信号通过数据采集器传输至上位计算机进行显示,两种电流曲线如图3所示。
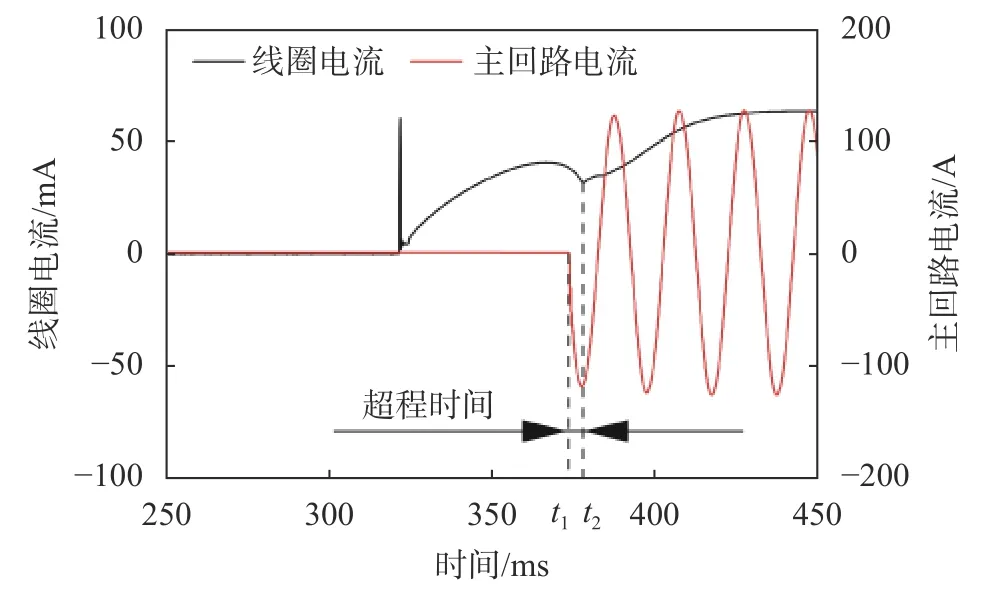
图3 接触器吸合过程的动态波形
由线圈电流曲线及主回路电流曲线可计算出接触器的超程时间。根据国家标准GB/Z 22200—2016《小容量交流接触器可靠性试验方法》中的定义,超程时间是动、静触点第一次接触时刻开始至衔铁完全闭合的时间间隔[3]。图3中,主回路电流于t1时刻开始从0发生变化,此时主回路导通,为动触点与静触点第一次接触,线圈电流曲线变化趋势先上升再下降,于t2时刻继续上升,此时为衔铁完全闭合时刻。根据定义计算可得超程时间为:t2-t1。由于样品间初始超程时间存在个体差异,故将超程时间退化量xj作为接触器性能退化的评价指标,定义为:

试验测试得到不同电流条件下接触器的超程时间退化量如图4所示。
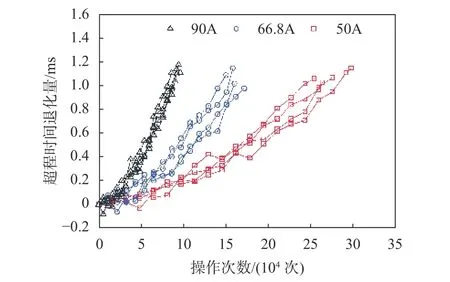
图4 加速试验退化数据
2 基于非线性漂移Wiener过程的寿命预测模型
2.1 非线性漂移Wiener过程理论
Wiener过程是一种时间连续且具有独立增量的随机过程,又称为布朗运动,用来描述小颗粒的无规则运动。适用于微小损伤逐渐累积而导致产品最终失效的非单调退化过程。一般地,Wiener过程{B(t),t≥0}满足:1)B(t)在不同时间段的增量彼此独立;2)B(t)初始值B(0)=0;3)对于 ∀t, Δt>0,增量B(t+Δt)-B(t)服从
在实际应用时Wiener过程常有多种变形,其中带线性漂移的Wiener过程主要适用于设备的退化率可近似为常数的情况。设备实际运行过程中,环境及工况复杂多变,设备退化率往往随时间而变化,呈现出非均匀退化的特征,且在退化过程后期,退化易得到加速,呈现出一定的非线性特征,带非线性漂移的Wiener过程作为一种非线性退化建模方法,可对本质非线性的随机退化过程进行研究分析[8]。一般地,初始退化量为0,则带非线性漂移的Wiener过程一般形式可描述为:
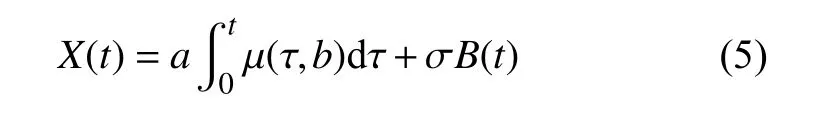
式中:X(t)——设备实际运行过程中t时刻的退化量;
a——漂移系数,表示个体差异性,假设
σ—— 扩散系数,表示外部干扰等随机因素对性能退化产生的影响;
B(t)—— 标准Wiener过程。
经验表明,绝大多数退化过程都服从幂函数法则。根据式(5)定义幂函数非线性Wiener模型为:
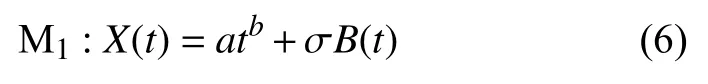
另外考虑线性模型及指数函数非线性Wiener模型,定义如下:
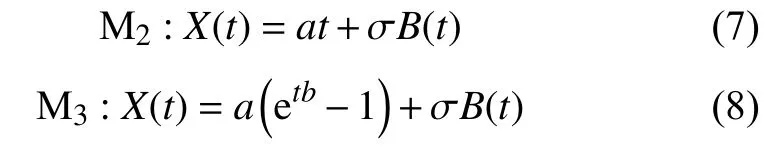
模型 M1中,非线性函数 μ (τ,b)=bτb-1,模型M3中, μ (τ,b)=bebτ。若令模型M1中b=1,则幂函数非线性Wiener模型M1退化为线性模型M2,可知线性模型M2是模型M1的特殊情况。
2.2 剩余寿命预测模型
根据文献[14]关于设备寿命的研究,可将接触器的电寿命定义为性能退化过程中,超程时间退化量首达失效阈值 ω时接触器的操作次数。若根据历史退化数据,预测出在第nd次操作时,距离超程时间到达失效阈值所需操作次数nk,即为接触器剩余寿命,原理如图5所示。
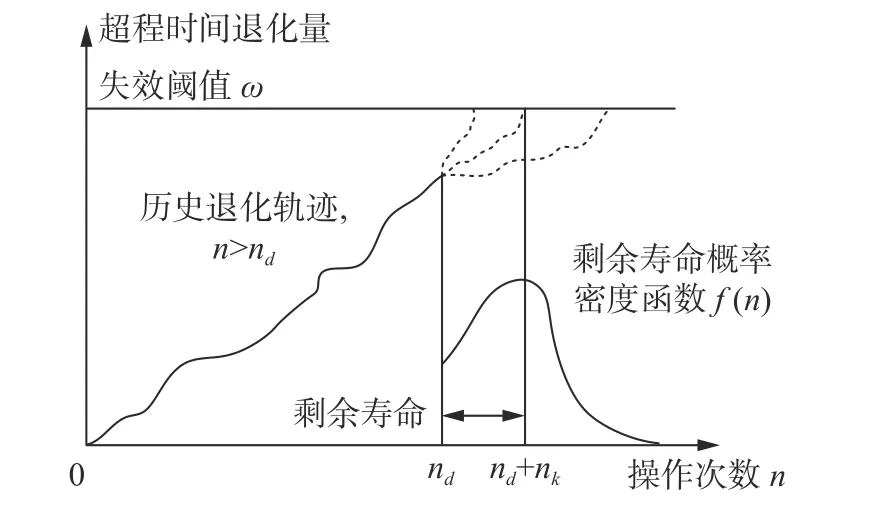
图5 基于失效阈值寿命预测原理图
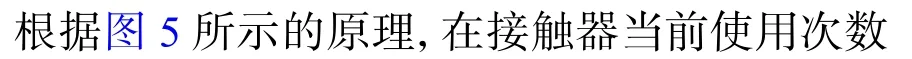

2.3 极大似然估计法估计模型参数


2.4 基于遗传退火算法的参数寻优方法
遗传退火算法(GASA)是一种结合遗传算法的全局搜索能力和模拟退火算法局部搜索能力的优化算法。在传统GASA算法原理[15]基础上,通过变退火步长,实现最大化剖面似然函数。变步长遗传退火算法流程图如图6所示。
图6 变步长遗传退火算法流程图
其中,变步长退火过程为:
1) 初始退火状态为s0,初温T0,计算初始目标函数值f(s0),确定每个温度下的迭代次数Lmax,对迭代次数Li=1,2,···,Lmax,重复步骤2)至步骤5);
2) 在个体旧状态si上施加较小步长的随机扰动λ1δi产生新状态
5) 若未接受新状态则将当前扰动的按 2k2倍减小,若连续n′次未能接受新状态则进行降温操作;
6) 判断是否满足结束退火过程条件,若满足条件则结束退火过程,进行遗传寻优操作。
3 实例分析
3.1 加速条件对常规条件寿命映射
通过对各样品的寿命对数值及电流的对数值按照式(2)进行最小二乘拟合得到加速模型的系数,拟合结果及评价指标如表2所示。
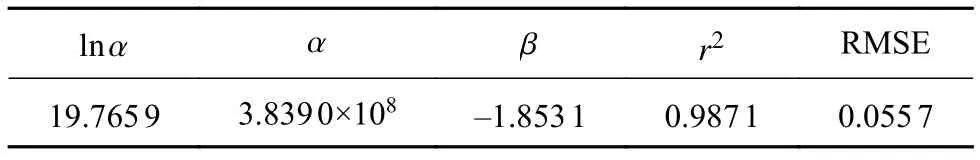
表2 最小二乘拟合结果
拟合结果表明,加速试验所得数据中的寿命对数值与电流对数值之间具有良好的线性关系,拟合结果也表明接触器电流加速退化过程符合逆幂律模型。根据逆幂律模型可知,不同电流条件下设备寿命可通过加速模型进行映射,映射关系如下式所示:

式中:np、nq——工况 p和 工况 q条件下的寿命;
Ip、Iq——工况 p和 工况 q的电流值。
通过式(18)可将3种加速工况下的退化过程映射至常规工况,映射所得12个试验接触器在常规条件下的退化数据可用于求解2.2节中所建立剩余寿命预测模型的PDF,实现接触器常规工况下的剩余寿命预测。
3.2 模型试验与验证
根据加速试验样品的超程时间退化量,其中9个样品的退化数据用于模型参数估计,剩余的3个样本作为模型验证。将超程时间退化量的均值作为接触器失效阈值,分别采用模型M1、M2、M3对退化数据进行建模,利用极大似然估计法结合变步长遗传退火算法对模型参数进行估计。采用AIC准则和寿命预测的均方误差(MSE)对模型拟合度进行检验。AIC准则在工程实践中用于模型选择,采用AIC准则可平衡对数似然函数值与复杂程度,防止过参数化问题。MSE指寿命估计值与真实寿命之差的平方的期望值,常用于衡量寿命分布的拟合程度。AIC值的计算方法为:
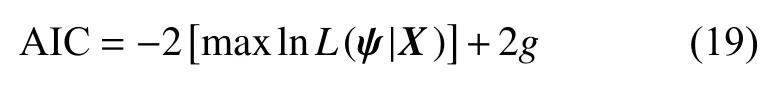
式中: m axlnL(ψ|X)——极大对数似然函数值;
g——拟合模型中参数的个数。
MSE值计算方法为:
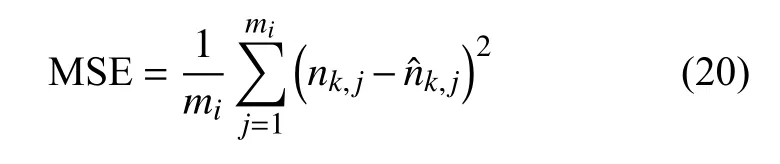
式中:nk,j——第j次监测时的真实剩余寿命;
AIC值与MSE值越小,表示模型的拟合度越高。各个模型的参数估计结果、对应的AIC值及预测寿命的MSE值如表3所示。
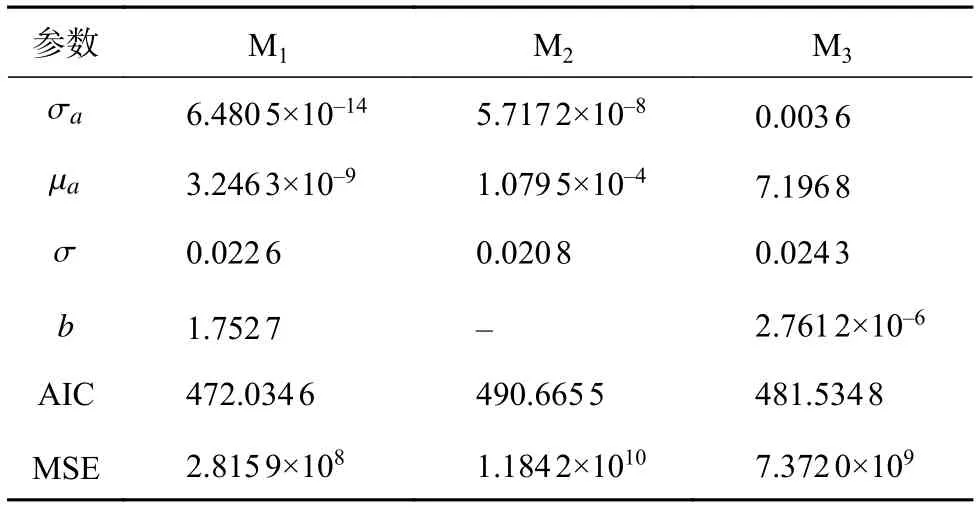
表3 3种模型的参数估计结果
根据表3可知,3种模型中,模型M1的AIC值及MSE值最小,拟合度最高。3种模型的拟合效果及对应的PDF如图7所示,图7(a)、(b)、(c)为剩余寿命PDF及预测结果图,以接触器在第nj次操作时的PDF的最大值近似为对应时刻的接触器剩余寿命,图7(d)中为3种模型的预测剩余寿命与实际寿命曲线。
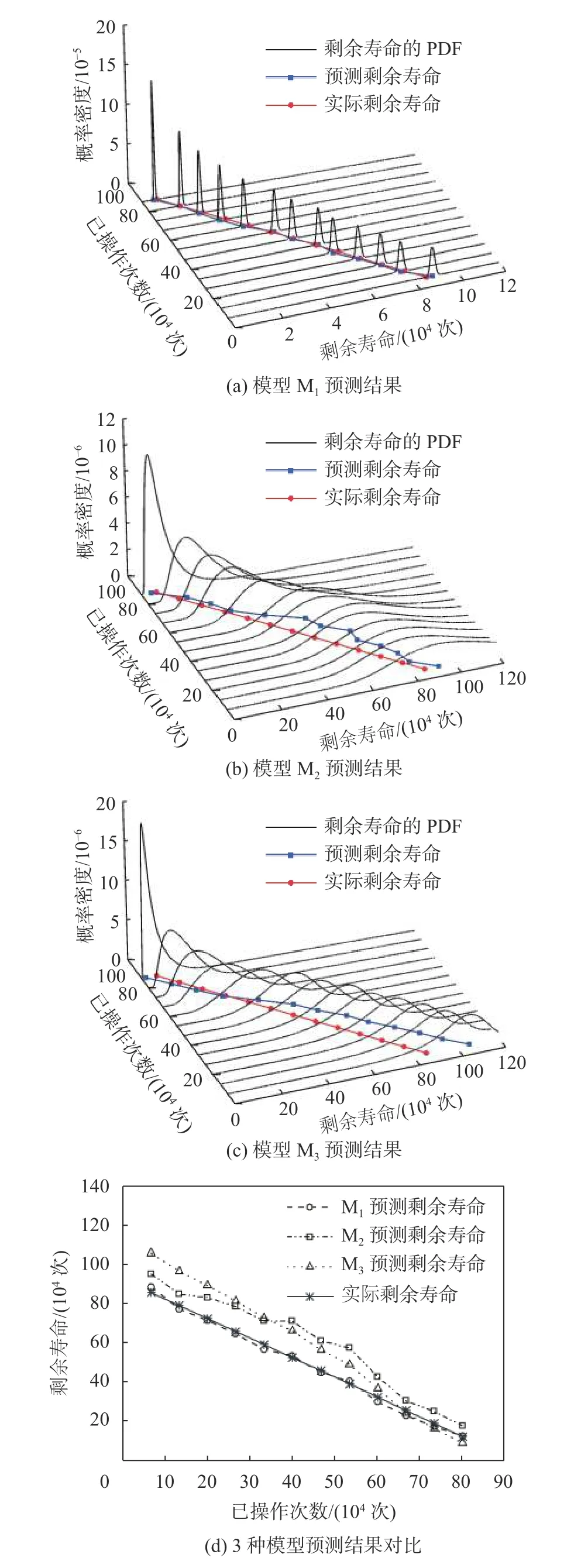
图7 模型M1、M2和M3预测结果
综合表3中拟合度计算结果和图7中拟合结果可知模型M1的预测结果与真实剩余寿命最接近。采用3个检验样品对模型M1进行误差分析验证,预测误差结果如图8所示。
从图8中可知,幂函数非线性Wiener模型M1的预测结果在接触器退化前期绝对误差较大,随着退化数据量增多,绝对误差整体减小。预测结果的相对误差率较为稳定,3个检验样品的最大相对误差率为12.3%,表明幂函数非线性Wiener模型对接触器剩余寿命预测误差率较小,预测效果较好。误差分析结果验证了幂函数非线性Wiener模型用于工程实践的可行性。
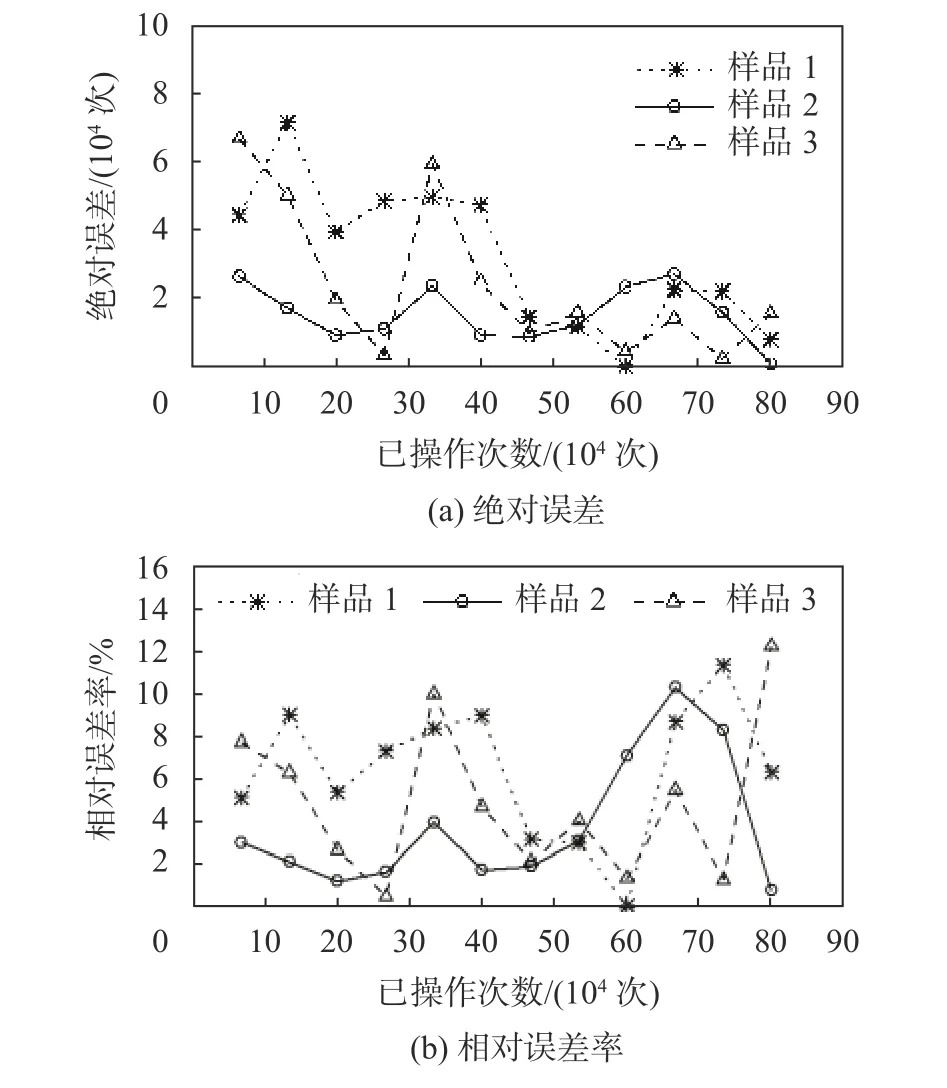
图8 预测结果误差分析
4 结束语
本文针对高速列车冷却风机接触器寿命预测的关键问题,以超程时间作为衡量接触器性能的特征参数,基于加速理论设计加速试验,确定接触器超程时间退化量的失效阈值,并通过逆幂律模型将试验数据映射至常规工况。基于非线性Wiener过程建立了接触器剩余寿命预测模型,提出极大似然估计法结合变步长遗传退火算法对模型参数进行估计。通过检验样本对3种模型进行了拟合度检验,结果表明幂函数非线性Wiener模型对接触器退化过程拟合度更好。对幂函数非线性Wiener模型进行了误差分析,总体预测误差均小于12.3%。综上所述,本文建立的接触器剩余寿命预测模型对科学规划接触器检修和更换周期,保证高速列车运行可靠性及降低运维成本具有重要意义。

