井下复合定位系统框架
范涌高,周怡敏,张玉玺,闫宋锟,朱丽娜
(1.中国电子科技集团公司 第三十六研究所,浙江 嘉兴 314000; 2.西安电子科技大学 通信工程学院,西安 710071)
0 引言
复合定位系统技术是一种包含粗定位和高精定位在内的技术,可以实现系统的精确定位功能,可以应用到通信、军事、民生等各种领域。本文从矿井下的应用开展研究。
煤炭是我国重要的能源供给来源[1],但是煤炭资源很大部分都在地下[2],这就对开采增加了困难,尤其在我国,煤炭资源的开采大都需要以开井的方式来进行[3-5]。然而由于井下环境复杂,作业人员发生危险的可能性很大[6-8],因此,对井下作业人员进行实时的位置监控,尤其是在发生矿难等特殊情况下的人员快速定位,是实现及时救援和人员管理的重要保障。然而,井下作业人员的位置持续在变化,这导致采集定位相关信息的过程中,位置信息的滞后性。而在这种移动环境中,会涉及到数据可用性和安全性等重要问题[9-11]。这对快速持续的定位提出了巨大的挑战。
为了解决这个问题,目前已有了很多可参考的工作。为了实现多目标定位,有研究学者提出了一种基于时差定位的算法[12-15]。该算法需要先关联目标,然后根据时间差定位多个目标。但是目标关联所需的时延较高,无法满足实时位置监测的要求。尤其是发生矿难特殊状态下,地下设备大概率损毁,这类方法很难实现对深埋地下的人员定位[16]。同时,此类方法的定位精度也与各数据收集节点的工作时间息息相关,因此若有数据采集节点出现了暂时的毁坏,定位精度会大打折扣。此外,在[17-19]中,广泛使用了纯方位定位技术,通过计算多个监测节点采集到的目标的方位角来实现简单的目标定位。此类方法更适合用于对静止目标进行定位,在这种情况下可以获得较高的定位精度。然而一旦目标开始移动,单纯的使用纯方位定位技术只能得到移动目标在上一时刻的位置,无法及时判断出移动节点的位置。因此该方法虽然简单,但是在复杂的移动环境下会出现定位出过多冗余节点、无法确保定位精度问题。总的来说,研究设计一种可以预测移动目标位置的定位方法是实现实时监控井下作业人员位置的重要前提。
在本文中,我们提出了一种井下复合定位系统框架。该方法包括粗定位和高精定位两部。面向井下场景,首先,我们提出了一种基于层次聚类的粗定位方法,利用目标测向数据,可以对目标进行范围定位,给出目标所在范围圈。第二部利用现有的高精度定位技术,在范围内高精度搜索,最终可以实现对目标的高精度定位。
本文的后续安排如下。第一部分介绍了基于层次聚类的粗定位方法。在第二部分,进行了综合仿真以验证所提出方法的有效性。最后,我们在第三部分总结了这项工作。
1 井下复合定位系统框架
本文提出的井下复合定位系统框架重点面向井下人员和设备定位。该系统主要包括粗定位和高精定位两步。
为了快速检测井下人员或设备目标的位置,本文提出先对目标进行粗粒度的定位,即利用简单的测向设备,采集目标的纯方位测向信息,在此基础上提出了一种基于层次聚类的粗定位方法,该方法支持对监测节点采集到的信息进行检测、关联、组合和估计处理,实现信息融合和信息冗余并快速响应移动节点的变化。具体来说,我们首先使用纯方位定位算法作为初始定位方法,记录移动节点可能的位置。然后,基于复杂的监测信息,我们再利用层次聚类算法来计算多个监测点同时检测到的移动节点的位置。通过这个粗定位方法,我们可以缩小定位范围,从而降低高精度定位设备的使用数量,进而降低成本。
在粗粒度定位后,已经获取到目标的范围信息,在该范围内,进行高精度定位设备的使用,如能实现1米以内精度的RFID定位、UWB等定位技术,进而可快速捕获目标的高精度位置信息。
由于现有的高精度定位方法和设备已有较多研究成果[20-26],但当前的测向粗粒度定位方向,目前使用较多的还是交叉定位方法,具有定位出冗余节点、定位精度差等问题,因此本文提出了一种新的利用层次聚类技术实现粗定位的方法。
2 基于层次聚类的粗定位方法
在本节中,我们将详细介绍所提出的定位方法。首先,我们采用纯方位定位算法作为初始定位方法,将可能的节点位置记录在初始集合DI中。 然后,根据复杂的监测信息(如节点数、起始频率、终止频率、频率数、驻留时间、信号电平、方位角和置信度),计算DI中多个监测节点同时检测到的移动节点位置以获取拓扑结构。该方法主要包括以下6个步骤,流程如图1所示。
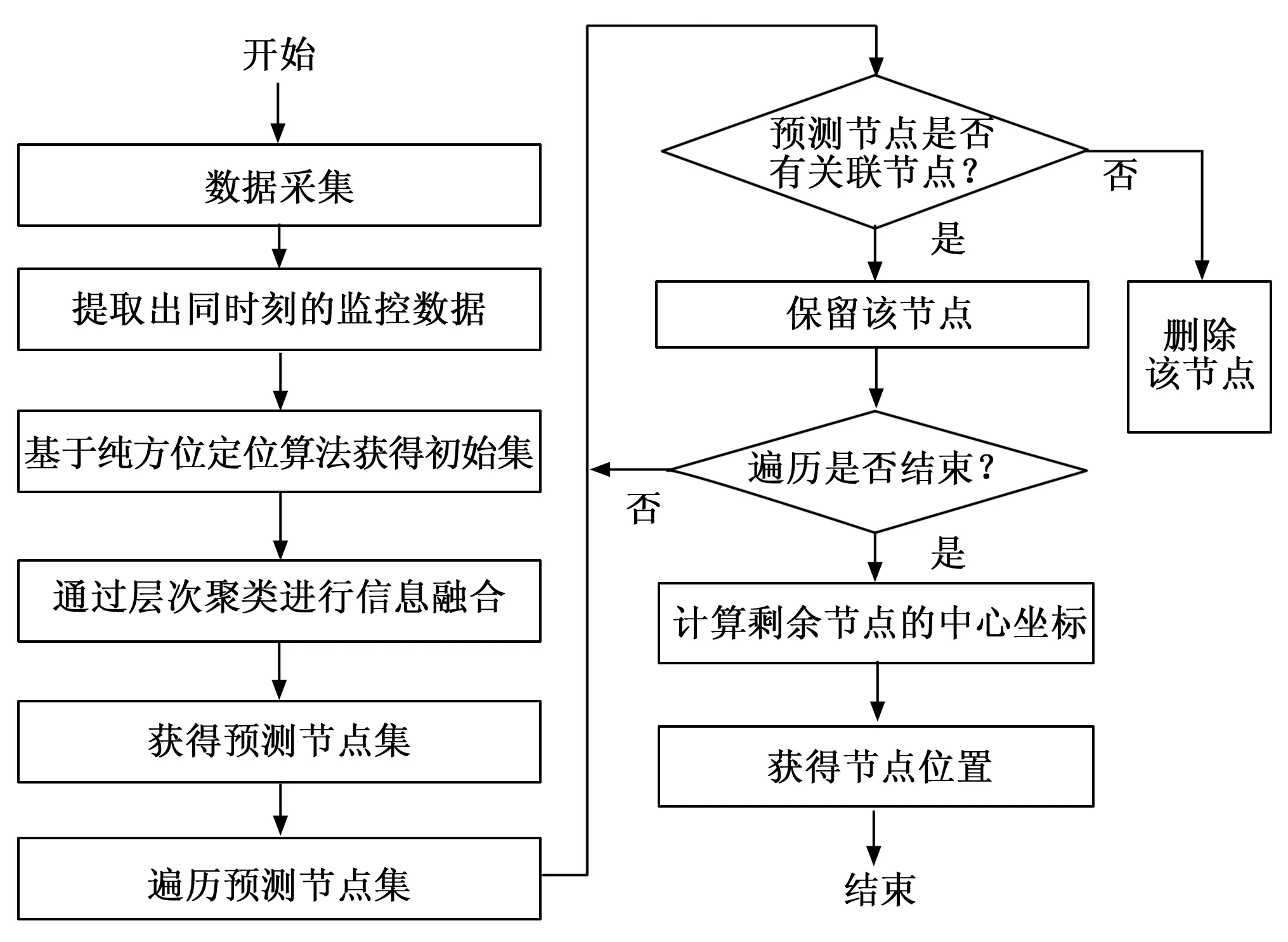
图1 基于层次聚类的井下定位系统流程图
1)场景初始化。假设有M个监控节点和N个移动节点(即井下作业人员),它们的通信范围都是r,监测范围为R。两种类型的节点都随机分布在该区域中。另外,每个监控节点的位置是已知的和固定的,而每个移动节点的位置是未知的和变化的。然后,通过监测节点收集移动节点的信息,为计算位置提供数据。供参考的节点分布如图2所示。在这个场景中,我们综合选择M4作为控制中心处理信息。每个节点的定位方法都是一样的。因此,我们引入以节点T为参考的井下定位系统,它同时被M1和M2检测到。
2)数据采集。监测节点向M4上报T的监测数据,包括节点编号、起始频率、终止频率、频率个数、驻留时间、信号电平、方位角、置信度等核心信息。
3)数据预处理。控制中心M4过滤出同时、同频采集的数据,再根据纯方位定位算法简单地计算出T的位置,并将结果记录到中。具体计算原理如下。
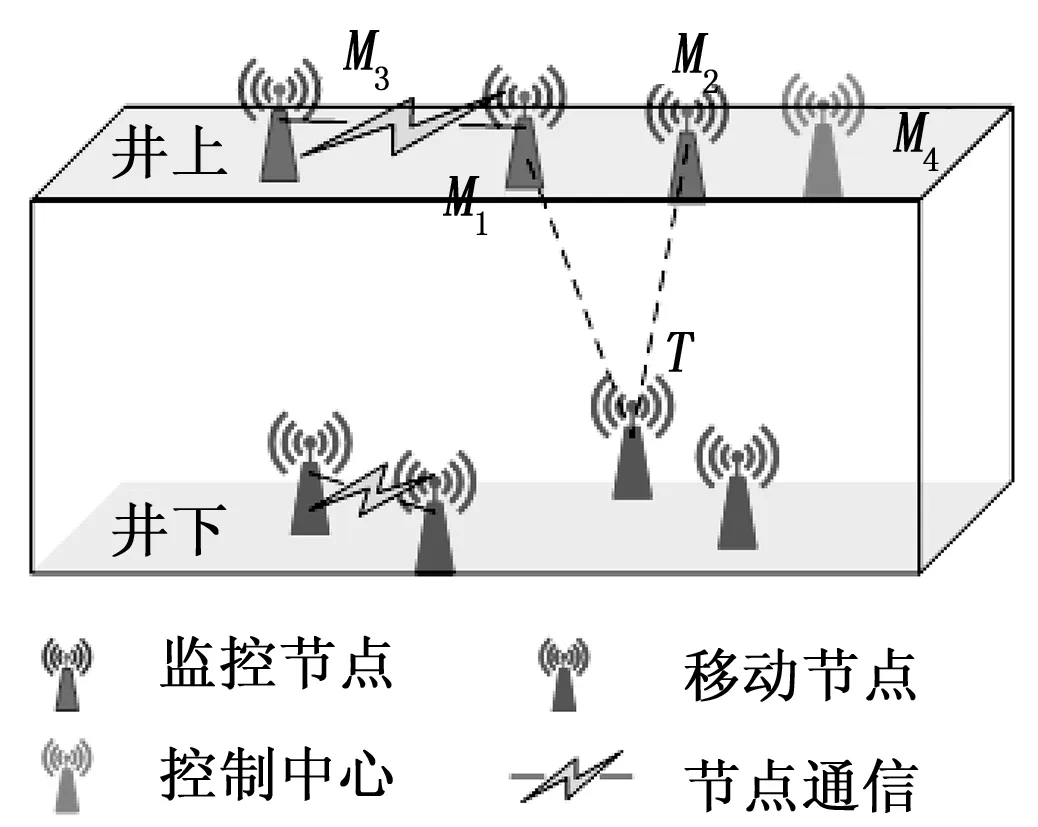
图2 节点分布情况
纯方位定位算法主要是基于两个监测点的数据,通过视线交汇得到交点位置,从而求得目标位置的方法。假设目标与监测点在同一平面运动。纯方位交汇定位算法原理如图3所示。
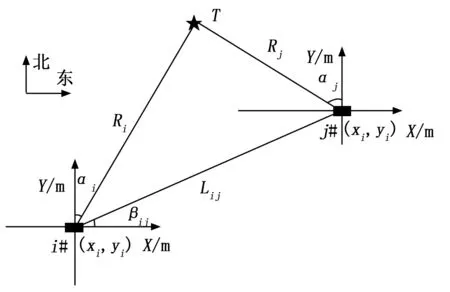
图3 纯方位定位算法原理
首先建立二维坐标系,假设监测点i、j的X轴指向方向为正东方向,Y轴指向方向为正北方向。两个监测点位置可由GPS测得,分别为(xi,yi)、(xj,yj)。两个监测点的距离即基线长度为Lij,基线与正东方向的夹角为βij,测得的目标方位角分别为αi,αj方位角区分正负:规定以正北方向为基准,顺时针方向取正值,逆时针方向取负值。
分布式监测点与目标的距离分别为Ri,Rj。由几何关系有:
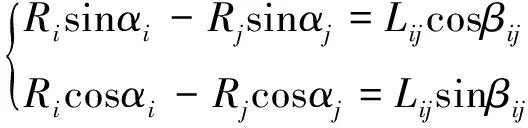
进一步可得:

由此可得,目标T的大地坐标:
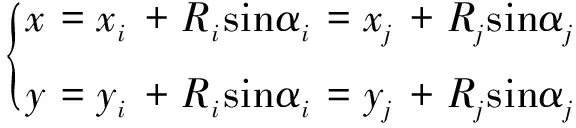
4)层次聚类。在实际情况下,所采集的T的信息可能会出现延迟,这意味着仅根据纯方位定位算法无法利用这些信息准确得到T的当前位置。因此,我们提出了一种基于层次聚类的位置预测方法,通过对现有完整数据和可能位置进行信息融合和冗余去除,提取关键信息并计算T的当前位置。然后将获得的位置记录到预测节点集DP中。
层次聚类算法分成凝聚的和分裂的两种,取决于层次分解是以自底向上(合并)还是以自顶向下(分裂)方式形成。所谓从底而上地合并,就是每次找到距离最短的两个簇,然后进行合并成一个大的簇,直到全部合并为一个簇,整个过程就是建立一个树结构。而自顶向下的策略首先是将所有对象置于一个簇中,然后按照某种既定的规则逐渐细分为越来越小的簇(比如最大的欧式距离),直到达到某个终结条件(簇数目或者簇距离达到阈值)。
考虑到多个监测节点采集到的信息都是分散的,若想要通过层次聚类获得目标节点的位置信息,采用凝聚的层次聚类方法是可行的。凝聚的层次聚类方法使用自底向上的策略,假设N个对象,开始时每个对象自己是独立的类,然后不断合并成越来越大的类,直到所有的对象都在一个类中,或者满足某个终止条件。合并过程中,找出两个距离最近的类合并形成一个类,所以最多进行N次迭代即可将所有对象合并到一起。具体的层次聚类流程如下:
步骤一:输入样本集合D,聚类数目k或者某个条件(一般是样本距离的阈值,这样就可不设置聚类数目)。
步骤二:将样本集D中的所有的样本点ci都当做一个独立的类簇。其中,ci表示第i个样本在集合D中的位置,坐标可以表示为ci={ci,1,ci,2,...,ci,ni}。ci,ni表示第i个样本的第ni个特征。
步骤三:计算两两类簇之间的距离,即ci和cj之间的距离D(ci,cj),其中i≠j,D(ci,cj)的计算方法如下:
D(ci,cj)=
步骤四:在所有的距离D(ci,cj)中,找出最小值D(cm,cn),即类簇cm和cn是距离最近的两个类簇。
步骤五:合并类簇cm和cn为一个新的类簇;
步骤六:重复步骤三至步骤五,直到达到聚类的数目或者达到设定的条件。
5)节点确认。利用时间、频率与历史轨迹匹配法,判断预测节点集中的点是否真实被监测节点探测到,若是,则该点作为探测到的移动节点位置输出;否则则删除该点。
6)节点坐标。对保留集合中的节点,计算中心坐标,即为最终预测点的位置。将预测点保存到控制中心。
3 仿真结果与分析
在这个部分,我们给出了基于层次聚类的粗定位方法的仿真结果,以验证其有效性。
3.1 仿真参数设置
我们假设在15 km×15 km的范围内对井下移动节点进行粗定位。具体地,以均匀分布的方式随机部署10~25个移动节点,以及8个监测节点。其中,移动节点按照随机游走模型移动,且监测节点不移动。监测节点的最大探测范围是5 km,模拟监测节点对移动节点的探测情况。通过我们所提出的移动节点定位方法根据监测节点的探测到的方位角、频率和监测节点的坐标计算并预测移动节点的位置。具体的仿真参数如表1所示。
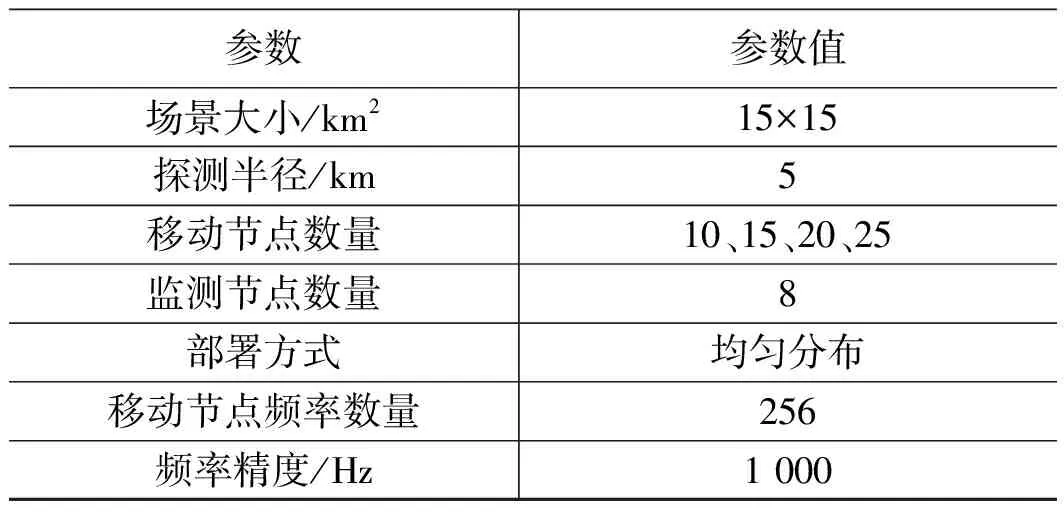
表1 仿真参数设置
3.2 仿真结果分析
图4给出了态势形成时间随移动节点数目的变化曲线。从图中可以看出,随着节点数目的增多,态势行程时间呈现明显增大的趋势,这是因为态势分析的算法的处理速度受数据限制,随着移动节点数目的增多,产生的数据量急剧增加,因此,态势形成时间增大。从图中可见,当移动节点数目为10时,态势形成时间仅为 0.068 s。当节点数目增加至25时,态势形成时间为0.929 s。
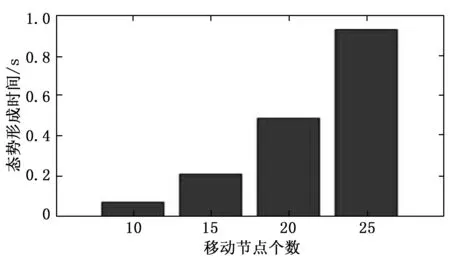
图4 态势形成时间随移动节点个数变化曲线
图5反映了位置误差随敌方节点个数变化趋势,节点增多,数据量变大,误差变大,但没有较大起伏,当节点数目较少时,可以将定位范围缩小至500 m左右。图6描述了位置与节点个数的关系。从图6中可以看出本文所提出的定位方法的位置预测精度可达到100%。图7描述了移动节点的拓扑关系。可以看出,随着移动节点数目增加,拓扑预测精度依然能达到100%。因此,我们可以得出结论,我们的粗定位方法可以在缩小的定位范围内得到准确的节点位置和拓扑关系,且不会出现冗余定位。

图5 位置误差随敌方节点个数变化趋势
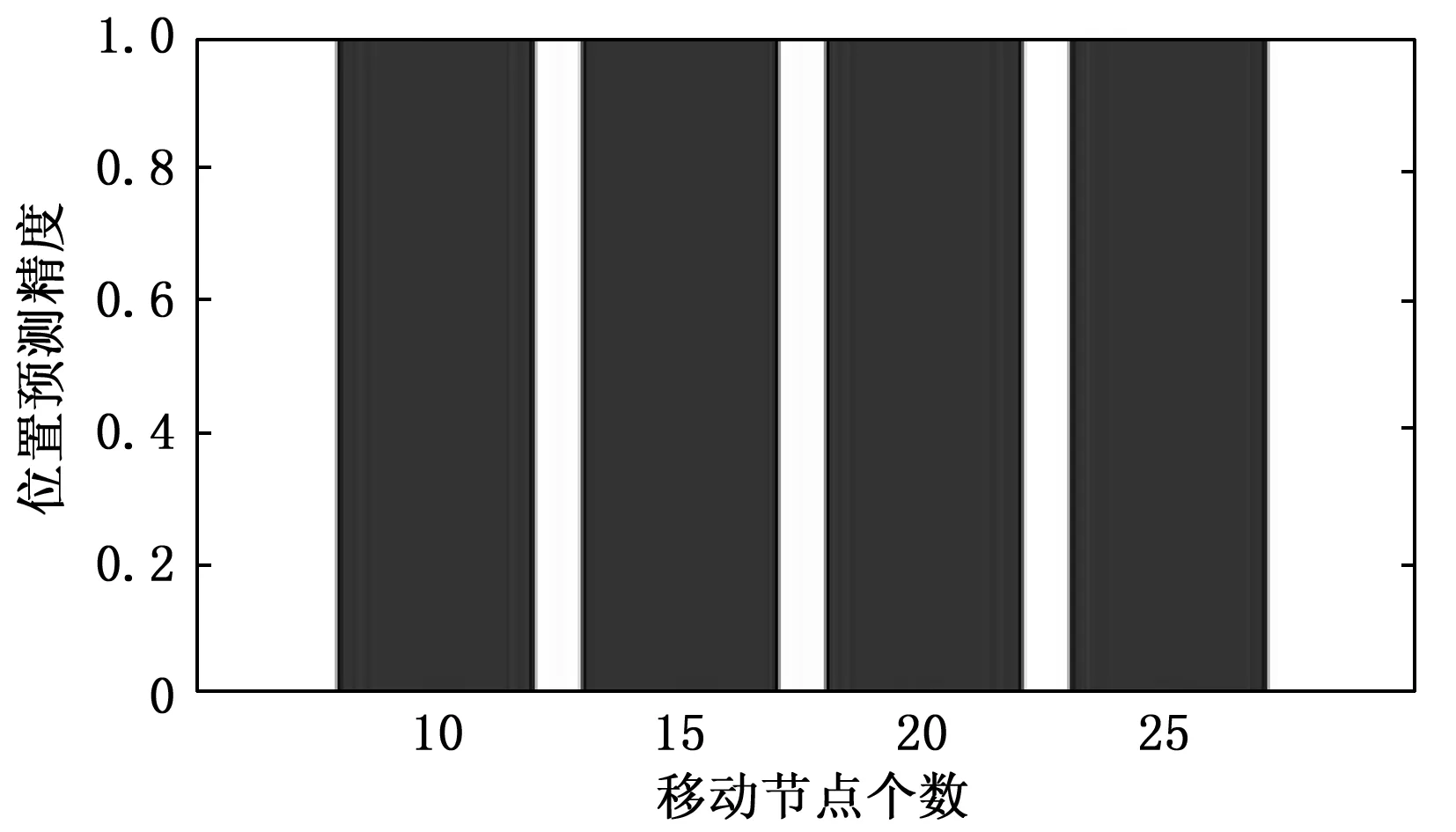
图6 位置预测精度随移动节点个数变化趋势
图7 拓扑预测精度随移动节点个数变化趋势
从图8、9中可以看出,数据融合后的信息数大幅度减少,说明了融合算法的有效性。图8显示了信息数量与去冗率随移动节点数变化的趋势,即使在高密度移动节点个数下,也能保证98%以上的去冗余率。图9表示信息数量与关键信息提取率随移动节点数的变化,在低节点密度时,可以保证100%的关键信息提取率,在高节点密度下,也可以保证98%以上的提取率。

图8 信息数量与去冗率随移动节点数变化曲线
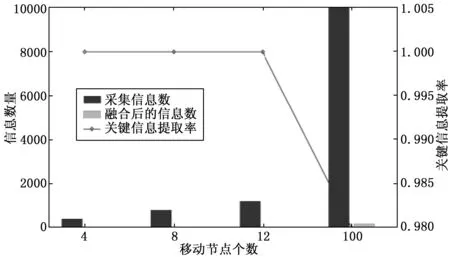
图9 信息数量与关键信息提取率随移动节点数变化曲线
4 结束语
在本文中,我们提出了一种井下复合定位系统框架来监测移动节点的位置变化,其分为粗定位和高精定位。我们研究了一种基于层次聚类的粗定位方法,可以缩小定位范围,并确定范围内节点的个数与拓扑结构,从而减少高精度定位设备的布设数量并降低成本。具体地,我们首先提取出同时、同频采集的位置数据。然后,使用纯方位定位算法作为初始定位方法。随后,为了克服信息滞后的问题,我们使用层次聚类算法进行数据融合,通过对现有完整数据和节点可能位置进行信息融合和冗余去除来预测位置。最后,我们对所提出的系统进行了全面的模拟。仿真结果证明我们的方法是有效的。该方法可以将定位范围从15 km缩小至500 m,并能得到范围内准确率为100%的节点位置和拓扑关系,且不会出现冗余定位。

