基于RTEthernet改进的时钟同步算法

陈佳佳，张凤登，张宇辉

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

RTEthernet(Real-Time Ethernet)是一种可以兼容传统以太网协议的实时以太网。RTEthernet在以往的物理层和数据链路层之上增添了会话层，并且使用了“通信循环”的概念来分时传输实时性消息和非实时性消息。

国外在时钟同步理论研究的起步是比较早的。1978年，Leslie Lamport在文献[1]中提出了逻辑时钟的概念，逻辑时钟这一概念的提出给内部时钟同步技术的发展提供了前提条件，通过在分布式实时系统内部建立一个虚拟的全局时间来实现各个节点之间的时间同步。

2004年，Kopetz等人在其著作[2]中提出了将状态同步与速率同步相结合的方法，并对主从式，非主从式同步进行了实验。实验表明，将状态同步与速率同步相结合能有效提高同步的精密度。对于不同的系统模型、同步精密度要求和容错能力等方面，衍生出了各种各样的时钟同步算法。综合远程时钟读取技术、算法容忍故障类型、系统通信模型等方面，可将算法大致分成了三类[3-4]：确定性、概率型和统计型。

通过对RTEthernet协议通信原理及其基础时钟同步算法进行了研究，并且考虑拜占庭故障对系统时钟精密度的影响，引入了滑动窗口技术来提升时钟同步算法容错性，提出了具有更高容错性的时钟同步算法——滑动窗口时钟同步算法。

1 系统结构及原理

1.1 RTEthernet体系结构

RTEthernet是保留了传统Ethernet的物理层和数据链路层的实时以太网。在这个基础上引进了“全局时间”的概念，同时还用了ISO/OSI参考模型的会话层进行报文的再封装。RTEthernet不仅可以兼容传统以太网，而且可以通过用时分多路访问(TDMA,time division multiple access)的通信方式进行基础报文的传送，提高了传统以太网的实时性和安全性。ISO/OSI、Ethernet和RTEthernet的体系结构如图1所示。

图1 ISO/OSI、Ethernet和RTEthernet的体系结构

1.2 RTEthernet通信结构

RTEthernet协议以确定性定时通信为基础，其通信方法是基于周期性重复的循环通信。因此，需要提前建立循环通信和时间窗口的大小， RTEthernet的整体情况表示如图2所示。图中的矩阵从宏观上展现了RTEthernet的工作原理。

图2 RTEthernet通信原理

2 同步时钟的概念及FTA算法

2.1 时钟同步

时钟同步算法的主要目标是要保证处理器的时钟差异不超过某个定值。在保证一定时钟同步精度的前提下，降低节点在时钟同步过程中的能量消耗，延长节点的生命周期是设计时钟同步算法的首要考虑。保证分布式系统中各个节点的时钟彼此同步成为保证分布式系统实时性的基础。

2.2 误差来源

分布式实时系统中的节点需要交换各自的时钟信息来实现建立全局时间。它们通过通信网络连接，在发送和接受各自本地时钟时都需要一个真实存在的处理时间。因此在时钟同步中需要考虑通信延迟的存在，不然将会直接影响到最终算法的性能。而且节点中的处理器、时钟、通信的链路等组件都有可能发生故障。故障主要可以分成七类，其中最重要的是时钟拜占庭故障。分布式系统中的任意节点都有可能遭遇某一种故障或几种故障混合，这时我们称该节点为故障节点，否则称之为无故障节点。文中考虑的是一般性故障和最恶劣情况(拜占庭故障，如图3所示)下的情况。若分布式系统可以通过某时钟同步算法容忍最恶劣情况下的故障，则说明这个算法是有效的。时钟同步算法的容错性主要体现在系统对拜占庭故障节点的容忍性这方面。

图3 时钟拜占庭故障

2.3 时钟同步的衡量指标

为了衡量系统中各个时钟的行为是否达到同步，引入了准确度Ψ、时钟偏差Δ和精密度φ这几个指标来衡量。偏差Δ：具有相同分辨率的两个时钟在同一单位微节拍上的偏移，即两个时钟速率的相对差，表示为：

(1)

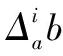
(2)

把有限时间间隔上的最大φi称为时钟集合的精密度。如果精密度φi小于某个期望值，就表示系统的内部各个节点之间相互同步，反之，就没有达到同步。

(3)

2.4 FTA算法

传统的容错算法FTA容错均值算法是通过对修正项进行筛除提高修正项的准确性。FTA算法是一种单轮算法，能够对不一致的信息进行处理，避免因为信息不一致引入的错误。该算法是从传统的“平均技术”发展而来的，并且在其中融入了去除极值的思想，于是形成了基础的时钟同步算法，FTA算法在一定基础上提高了分布式系统时钟同步的容错性，算法过程如图4所示。

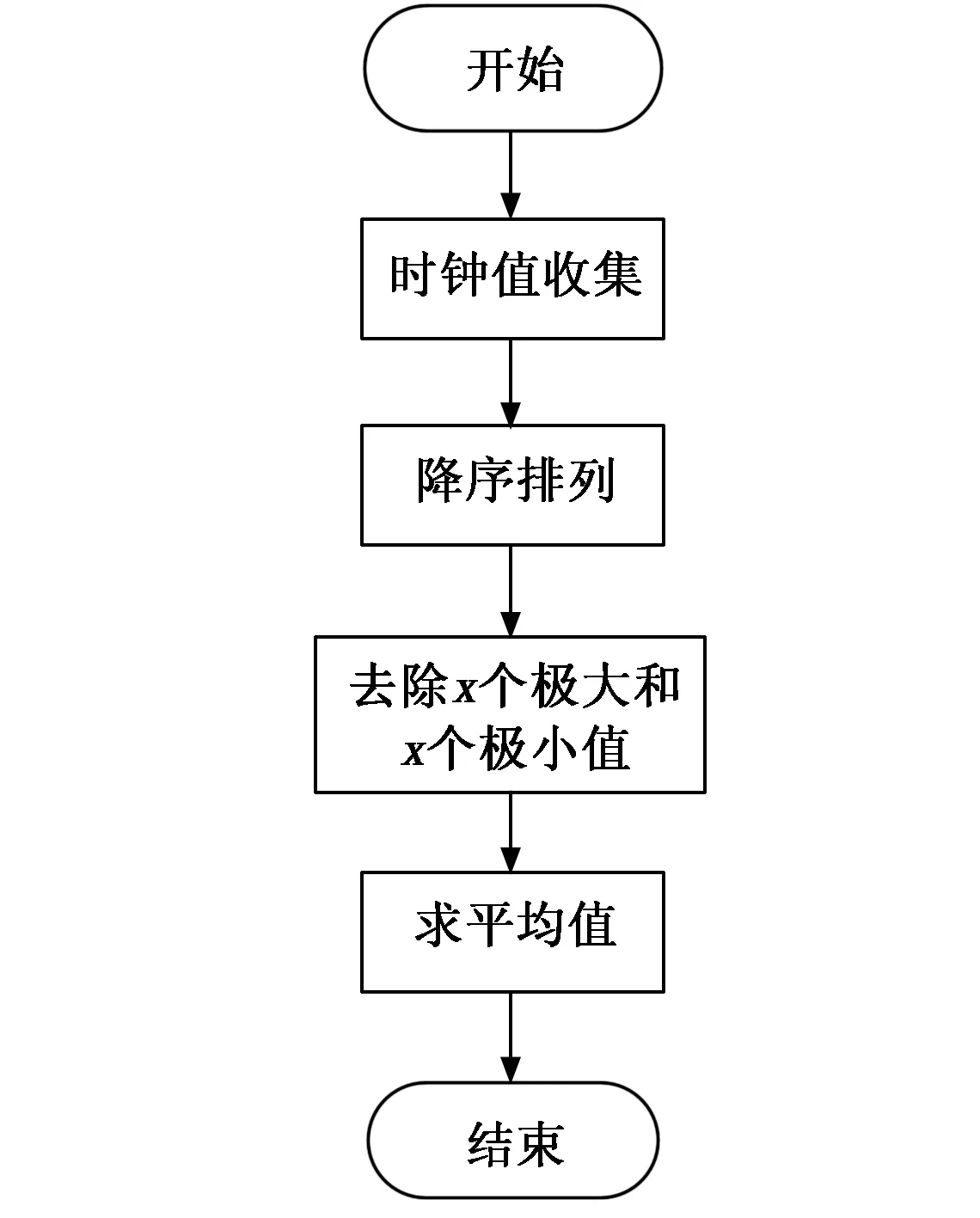
图4 FTA算法同步过程

3 滑动窗口时钟同步算法

3.1 滑动窗口技术

滑动窗口是一种流量控制技术。在早期的网络通信中，通信双方没有考虑网络的拥堵情况而直接发送数据导致了中间结点阻塞丢包，双方都不能发送数据，所以就有了滑动窗口机制来解决此问题[5]。后来，由这一技术衍化而来的滑动窗口算法不仅大量运用到了通信领域，在其他各个领域之中也得到了广泛地应用，例如图像处理，轨迹预测及其他进行数据预测、优化的领域。滑动窗口算法和滑动窗口技术是一样的，只是应用的场景不一样，可以根据需要调整窗口的大小，也可以固定窗口的大小[6]。

滑动窗口技术是在给定的特定窗口大小的数组或字符串上执行要求的操作。该技术可以将一部分问题中的嵌套循环转变为一个单一循环，因此它可以减少时间复杂度。下面举例简单说明滑动窗口技术的原理。如图5所示，我们假定有一组数：-2,3,1,5,4,0,7,1,-1,求出波动最小相邻的4个元素。因此，我们将窗口大小设定为4，当滑动窗口每次划过数组时，计算当前滑动窗口中所有元素的方差。图5可以方便看出滑动窗口技术可以用来解决一些满足一定条件的连续区间的问题。由于区间的连续性，当区间发生变化时，可以通过既有的计算结果对搜索空间进行裁剪，从而减少了重复计算，节省了时间。

图5 滑动窗口示例

3.2 容错滑动窗口算法的描述

根据文中对容错能力的改进，下面以为伪代码的形式描述第i轮同步中节点k使用容错滑动窗口算法进行时钟同步的过程：

1)函数及符号的定义，见表1：

表1 伪代码参数

2)算法描述

算法：容错滑动窗口算法

输入：重同步时间

输出：本地节点即将应用的校正项

1.WhileTkNOW=Tido/*当任一节点当前的逻辑时钟进入第i轮的循环时开始准备时钟同步*/

2.ARRki(k)=TkNOW //每个节点记录当前的时钟值

3. ifTkNOW=Tkithen /*如果任一节点的时钟值等于重同步时间，则将自己的时钟值发送给其他所有节点*/

4.send(message);

5.Pki[k]= ARRki(q)

6.end if

7.ifTkNOW=TNITithen

8.Qki[k]=discard(descend(Pki[k]))//将获取到的时钟值进行降序排列，然后去掉f/2个最大和最小的值

9.whilej≤n-2f+1then//获取所有窗口内的方差

10.Wj[k]= SWAj(Qki[k])

11. S[j]=variance(Wj[k])

12.end

13.MED=median(rest(Qki[k],Smax))//获取方差最大集合的补集，然后求得该补集的中值

14.ADJki=Tki-MED+δ//计算校正项

15.return(ADJki)

16.end if

17.end while

上述过程概括的来说，可将算法分为4个阶段：时钟值收集阶段、去极值阶段、滑动窗口阶段和求中值阶段。分布式实时以太网将通信的循环划分为了静态段、动态段和NIT段。每个节点在通信循环中NIT的开始时刻执行FTSW算法，如图6所示。

图6 NIT段的FTSW算法

下面将分别介绍FTSW算法的各个阶段。

1)时钟值收集阶段：所有要参与时钟同步的节点在通信循环的静态段时隙的开始处，通过通信帧帧头的第4位，向时钟集合中的所有其他参与者表明它将发送是同步帧，该同步帧的作用是参与网络的同步[7]。然后利用静态段发送的同步帧测量时间偏差来得到每个节点的时钟估计值，并存储在一个数列中，然后将数列中的时钟值按照降序排列，如图7所示。

图7 时钟值收集阶段

每个节点时钟在第r轮的重同步，可将得到的时钟值构造成一个时钟值矩阵，我们以节点k为例，节点k保存该矩阵的列和对角线上的元素。

(4)

对于无故障时钟有：

(5)

图8 去极值阶段

3)滑动窗口阶段：滑动窗口的大小为f，并且f为该系统能够容忍的故障节点数。该窗口从去极值后的时钟值序列的最左端开始，也就是第一个窗口是由第f/2+1个元素至第3f/2个元素组成的。然后，将窗口逐元素的向右滑动，直至窗口的最右边元素为第n-f/2个元素，即去极值后序列中的最右边元素。在这个过程中，一共得到了n-2f+1个窗口的数据集。最后，从这n-2f+1个数据集中找到方差最大的窗口，如图9所示。

图9 滑动窗口阶段

4)求中值阶段：利用滑动窗口阶段得出了方差最大的时钟值集，然后将这些时钟值剔除，最后对剩余的时钟值进行求中值，从而减轻时钟拜占庭故障对最终校正项的影响。

上述算法概括的来说，先将远程读取到的时钟值进行降序排列，然后去除f个极端值(f/2个最大值和最小值)，当f是奇数时将去除的极大值个数向上取整，去除的极小值个数向下取整。然后，对剩余的时钟值利用滑动窗口的思想求出方差最大的窗口，然后得到其补集。最后求取该补集的中值，若此时补集为偶数时求取中间两个值的均值，然后对该中值向下取整。最终，利用简单的代数运算就可以求得本地时钟的校正项。

从算法的实现上来讲，容错滑动窗口算法在FTA算法的基础上采用了容错中值的思想并且增加了求最大方差窗口的过程，这一过程有效地提高了系统的容错能力，这是该算法的显著特点。

4 算法仿真验证

4.1 系统模型的构成

实验用7个节点组成一个总线型的拓扑结构，该网络中的各个节点模拟RTEthernet协议进行通信。将节点3和6设置成拜占庭故障节点，把1,2,4,5,7节点设置成无故障节点，如图10所示为仿真系统拓扑结构。

图10 仿真系统拓扑结构

4.2 系统参数设置

根据文献[8-10]研究成果和RTEthernet通信模型对局部参数进行设置：系统中各节点初始同步的精密度设置为φint=20×10-6s，各个节点的最大时钟漂移率为ρ=10-4s，系统中传输延迟最小的为5×10-6s，延迟最多的为10×10-6s。即设置分布式系统内的消息传输延迟范围为[5,10] μs，因此该系统传输延迟的不确定度为2.5×10-6s，消息延迟范围的中间值为δ=7.5×10-6s。然后，考虑每个循环中包含了ST段和DYN段以及NIT段，将重同步周期长度设置为5 ms。节点参数设置如表2所示。

表2 系统节点参数

4.3 仿真结果分析

根据上述系统拓扑结构和参数的设置，本文将实验分为两部分，第一部分是无拜占庭时钟故障情况下对FTA和FTSW算法进行收敛性验证，第二部分是存在拜占庭故障情况下对FTA和FTSW算法进行容错性验证，运行结果如下：

1)当f=0与系统初始精密度φint=20 μs时，系统中的各个节点分别执行FTA算法和FTSW算法，最终将每次同步后系统的精密度绘制为如图11所示。

图11 无拜占庭故障情况下两种算法的时钟同步精密度对比

从图11可以看出，该系统中的各个时钟通过时钟同步算法进行过周期性的时间校正后，系统的时钟精密度会趋于稳定，并且当无拜占庭故障时钟的时候FTA算法大于FTSW算法。当考虑到传输延迟的误差后， FTSW算法的平均精密度约为22.28 μs，FTA算法的平均精密度约为23.15 μs。由此可以看出，在此系统中无拜占庭故障的情况下，原始算法的精密度还是比较优异的。

2)当f=1,2和系统初始精密度φint=20 μs时，系统中的各个节点分别执行FTA算法和FTSW算法，对FTA算法和FTSW算法进行比较分析和容错性验证。

由图12可以看出，当系统中节点3发生拜占庭故障时，经过FTA算法同步后该系统精密度为24.47 μs，当系统中的节点3和6同时发生拜占庭故障时，该系统的精密度为26.32 μs。由此可以发现，在一个由7个节点组成的系统中，当系统中存在两个拜占庭故障的时候，FTA算法的容错能力大大降低，系统的精密度下降了13.7%。

图12 出现拜占庭故障情况下两种算法的时间同步精密度对比

此实验是在时钟同步过程中通过环境变量控制一个节点(节点3)或者两个节点(节点3和6)，使其产生[0,200]之间的随机数(单位为μs)作为该节点的本地时间信息封装到同步帧并发送到网络，试图干扰其他节点的时间同步，但该节点自身真实的本地时间还是保持原来微节拍计数器的正常计数值。从图12可以看出，当一个节点发生拜占庭故障时，该系统的精密度为22.15 μs,当系统中两个节点同时发生拜占庭故障的时候，该系统的精密度为23.75 μs。

综上，在分布式系统中各个节点初始同步的情况下，存在最多不超过节点总数1/3的拜占庭故障节点的情况下，FTSW算法是收敛的，并且在无故障情况下，FTSW算法的同步精密度较高；当系统中存在拜占庭故障的时候，FTA算法的同步精密度损失了13.7%，FTSW算法的同步精密度损失了6.6%，FTSW算法的同步精密度比FTA算法的精密度提高了7.1%。

5 结束语

随着工业以太网的不断发展，电力、钢铁、工业制造、自动化工业等领域在以非常迅猛的速度往前发展。如果要实现从无线到有线的巨大变化，需要考虑到实时性和可靠性。随着分布式系统的应用越来越广泛，系统需要分配的节点也更多，因此发生故障的概率也越高。对于其中具有严格时间要求的系统中，时间同步变得越来越重要。工业以太网的时钟同步问题是一个比较关键的问题。在满足时钟同步的前提下，系统还需要具有一定的容错能力。RTEthernet是可以同时兼顾传统以太网的新型工业级的实时以太网协议，但是该协议的时钟同步算法容错性较低。文中引入了滑动窗口技术，得到了一种具有较强容错能力的算法，即FTSW算法。文中研究主要集中在确定性时钟同步算法，在后续的研究中可以考虑能否将统计型和概率型算法的思想引入到RTEthernet的时钟同步过程中。