基于超声相控阵的角焊缝缺陷信号重构方法研究

梁国安，姚叶子，郑 凯，许 倩，王海龙，王海涛

(1.江苏省特种设备安全监督检验研究院，南京 210036；2.南京航空航天大学 自动化学院，南京 210016；3.江苏长城计算机系统有限公司，江苏 南通 226000)

0 引言

当今社会，由于工程需要，在大量的工程设计领域应用到了接管角焊缝。例如，在制作和安装电站锅炉的过程中，为了方便现场施工作业，在汽包与接管的连接处就是采用了角焊缝的连接形式[1]。在电站锅炉的运行过程中，由于该部分的结构是不连续的，所以此区域存在应力过于集中的情况，并且由于温度场的不同，在此部分还会产生很大的温度差[2]。在锅炉长期运行中接管角焊缝一直是常见的失效单元，所以在锅炉定期检查中，此部分需要重点检验[3]。

目前在检测角焊缝内部缺陷的时候主要采用超声脉冲发射回波检测法[4]，它主要通过分析回波信号来判断缺陷的相关信息。作为一种典型的非线性、非平稳信号，超声回波信号中含有大量的有用信号，但是它在不同的介质中传播会产生一定的衰减效应，从而使得信号变得较为微弱[5]。除此之外，在使用超声进行检测的过程中，环境中不可避免的噪声会污染微弱的回波信号，这会一定程度地影响检测的精度[6]。因此，在进行回波信号分析之前需要采用有效的信号处理方法去抑制其携带的各种噪声，常用的降噪方法有小波去噪、经验模态分解(EMD，empirical mode decomposition)去噪等[7]。小波变换具有多分解尺度、去相关性等优势，对随机噪声的过滤效果较好，但是它也有阈值函数选取较为困难、分解层数多变等缺点；经验模态分解对于非平稳信号的处理具有较强优势，但分解过程较不稳定，去噪能力较差[8-10]。

为此，本文在进行角焊缝超声相控阵检测试验之后，首先提取裂纹与未熔合缺陷的A扫信号数据，然后通过 EMD 将提取到的原始A扫信号分解为多层本征模式函数(IMF，intrinsic mode function)，利用互相关准则提取IMF 分量进行重构。最后提出小波去噪和 EMD 相结合的角焊缝缺陷信号重构方法，比起单纯使用EMD分解，使用小波去噪对原始信号数据进行处理后，重构信号的信噪比较高，均方差较小，为进一步缺陷成像，缺陷回波信号特征提取模式识别打下良好的基础。

1 小波分析与EMD分解的理论分析

对于超声检测装置采集到的回波信号进行处理，这是相控阵检测角焊缝的关键一步，通过时域与频域的充分分析，能够较好地分析出非平稳信号的各种尺度信号特征[11-12]。本文主要基于小波分析和EMD分解方法对得到的缺陷信号进行分析。

1.1 小波分析

小波分析起源于20世纪50年代初的纯数学领域，在之后的近三十年间并没有引起人们的注意，近年来通过许多数学家与工程技术人员的努力探索，小波分析发展迅速，现已逐步成为热点研究方向之一，其在非平稳信号去噪处理等方面有着一定独特的优势，所以如今被广泛应用于信号处理、图像处理等工程领域，在科技信息产业领域取得了令人瞩目的成就。小波分析是通过对信号进行多尺度地细化分析，其可以分析到信号的任意细节，从而在时域和频域变换中提取有效的信息[13-15]，其具有对信号在不同范围、不同的时间区域内进行分析，对噪声不敏感，能够分析到信号的任意细节等优点，被誉为数学显微镜。使用小波变换对信号处理时，首先需要选择合适的小波函数，本文选择正则性好的Daubecins小波，该小波由世界著名的小波分析学家Ingrid Daubecges所构造，当其作为稀疏基时有较小的光滑误差，进而优化信号重构，使处理结果相对光滑。Daubecins 小波可以用dbN表示，N是小波阶数，在小波函数ψ在小波和尺度函数φ(t)中,支持区域和消失矩分别是 2N-1和N[16-18]。当采用更大的序列N的值，即选用更大的dbN小波阶次之后，消失矩阶数也会随之提高，有效增强其光滑性，从而优化频域局部化能力，进而呈现出更佳的频带划分效果。

在对信号去噪的过程中，首先是使用小波对原始信号进行分解，将处于较高频率的噪声分解出来然后再进行处理。在小波分解时，小波系数可以通过阈值和其他的手段来处理[19]，将小波分解后得到的各层小波空间的细节系数使用阈值对其进行截断作用，进而使得信号被小波变换或者其他方法进行去噪处理。以下是3种常用的去噪方法：

1)默认阈值去噪处理。该方法首先通过ddencmp函数生成信号的默认阈值，这个默认阈值是该方法的关键部分，后续的去噪过程由函数wdencmp来实现。

2)给定阈值去噪。该方法首先通过经验公式产生一个较好的阈值，这个阈值在实际的去噪过程中有着较高的可靠性。其重要步骤是阈值量化，函数wthresh可以用于实现阈值量化这一过程。

3)强制消噪处理。该方法主要通过将信号的所有高频系数置零，即对信号所有的高频部分进行滤波处理，然后在此基础上再重构信号。此方法具有简单直接的优势，能够达到使信号变得较为平滑的效果，但是由于强制去除了高频信号，这会使得信号的有用部分也可能因此而丢失。

1.2 EMD分解

在一般的情况下，大多数时间序列的分解方法均遵循一个原则，即在某个基本函数的系统上扩展序列，然后通过分析每个分量的展开系数和属性来分析该信号，但是超声相控阵的A扫信号为非平稳信号[20]。1998年，美国华裔院士NordenE.Huang等人对此提出了一种新的理论方法，即经验模态分解法，其对于分析非线性、非平稳信号序列有较好的优势。EMD分解是一种自适应的时频分解方法，其按照信号局部时间特征尺度自适应地将信号从高频到低频按序分解成一组尺度不同的固有模态函数，具体操作步骤为首先对一给定的信号获取其存在的极值点，然后通过插值的方法得到信号的包络，在得到均值之后与均值做差，从而获得分解的一层信号。通过上面的迭代过程，获得信号的分解结果为：

(1)

即l个IMF和一个残差r[8]。IMF定义是由Huang等人提出的，其需要符合以下的两个条件：(1)在一段数据中，极值点的个数等于过零点的个数，或者二者相差最多不超过一个；(2)任意一点由局部极大值点与局部极小值点形成的包络的平均值为零，即信号的波形局部对称[21]。第一个条件类似于传统的平稳化高斯过程中对于基带信号的要求，第二个条件将全局的限定变为了局部的限定，其有效防止了由于波形的不对称所形成的瞬时频率不必要的波动。

EMD分解将原本复杂的信号分解得到各个IMF分量之后，可以通过分析IMF分量进而分析原信号不同尺度的局部特征信号，并且将之前的非平稳数据加以处理使其平稳化。由于是基于信号序列时间尺度的局部特性进行信号分解处理，因此是随信号本身的变化而变化的，故而具有自适应性。并且由于分解过程中所使用的基全部来自于原信号，所以通过EMD分解的到的分解结果更加的有效，它的自适应性与时频聚焦性，适合运用于分析超声缺陷信号。

2 角焊缝相控阵检测试验

2.1 检测设备

本次实验采用的是仪器型号为TOPAZ 32的便携式超声相控阵设备,它是一款由ZETEC开发的全集成32通道超声相控阵检测仪，可同时激发32孔径进行自发自收或一发一收检测。本仪器最大数据传输速度为10 MB/s，数字化频率为100 MHz，增益范围为0～70 dB，支持512个聚焦法则。探头采用了有利于工业现场应用的AXL-2.25 MHz型号小尺寸探头，其阵元数为32个，阵元间距为1 mm，中心频率为2.25 MHz。楔块型号为AXL-55SW，角度为55°。

2.2 被检工件

由于接管角焊缝结构复杂，使得声场路径相对复杂，增加了超声检测的难度。本文以锅炉装置中接管处角焊缝为对象，制作了一块角焊缝试样，母管外径为1 600 mm、壁厚为75 mm，支管外径为426 mm、壁厚为28 mm，对此进行检测工艺研究。如图1(a)所示为试样被检工件的几何尺寸及坡口尺寸，图1(b)所示为被检工件的实物图。

图1 被检工件

2.3 检测结果

本次试验在检测接管角焊缝时将探头放置于距离接管150 mm处，具体检测参数如表1所示。利用二次波可以在试件中检测到多处缺陷，以危害性较为严重的裂纹与未熔合为例，检测得到两处缺陷，检测结果如图2所示，缺陷分别标为1号与2号。1号缺陷的检测结果如图2(a)所示，其为焊缝裂纹，裂纹缺陷在进行相控阵扫查的过程中声波没有固定的反射面，在图像上显得比较松散，并且由于马鞍形结构造成的波形散射，所以对其加12 dB补偿增益，得到的缺陷如图2中方框所示，最高幅值为88.5%。2号缺陷为焊缝未熔合，其检测结果如图2(b)所示，未熔合缺陷图像较为细长，仅为一层，从A扫信号也可以发现缺陷信号较为集中，最高幅值为69.0%。

表1 扫查参数

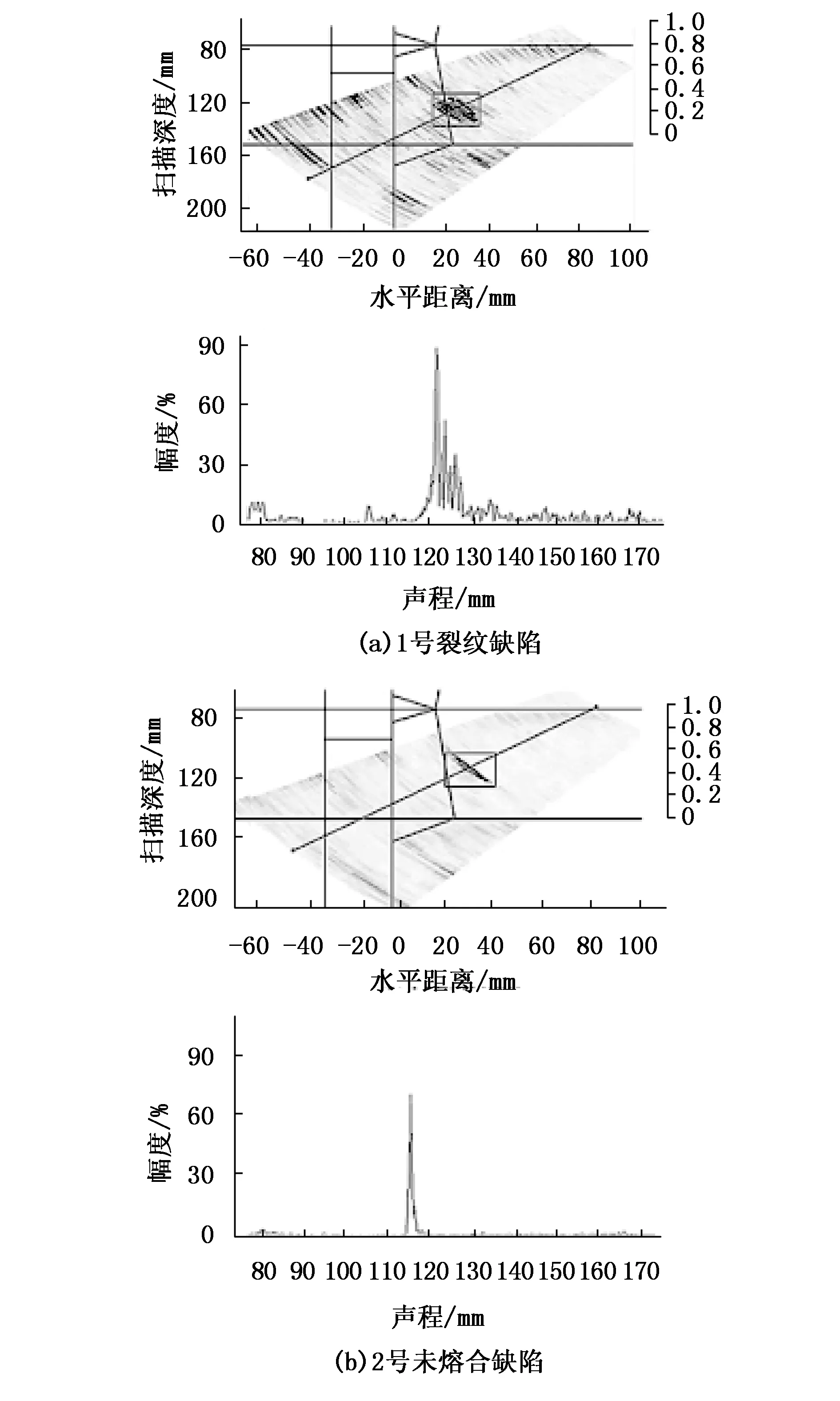
图2 超声相控阵检测结果

3 经验模态分解特征成像

本文主要针对1号裂纹缺陷与2号未熔合缺陷处的信号进行分析，得到裂纹缺陷的原始信号与频谱见图3(a)，得到未熔合缺陷的原始信号与频谱见图3(b)。接着按照本征模态函数分解的方法，分别对它们进行EMD分解，得到了8阶IMF分量，如图4～5所示，这8个IMF分量分别反映出原始信号在不同时间尺度上的信息，代表着一组特征尺度的数据序列，并且将其与残差累加后能得到原始信号。

图3 原始信号与频谱

图4 EMD分解1号裂纹信号的IMF分量

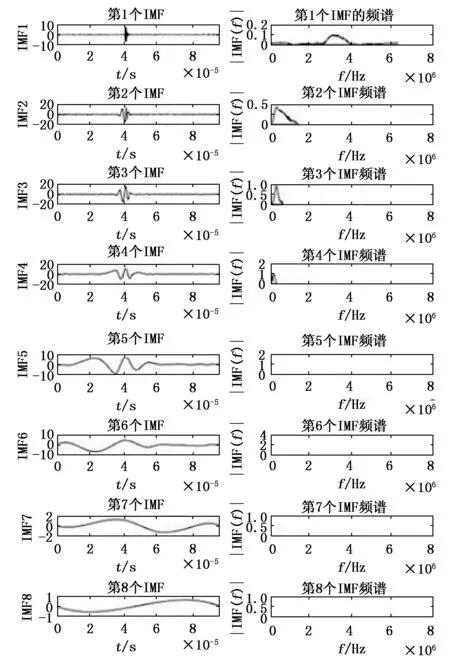
图5 EMD分解2号未熔合信号的IMF分量

信号通过EMD分解之后所获得的各个IMF分量中通常情况下会含有一些伪IMF分量，这些伪IMF分量不能够反映原始信号的特征，且与原始信号无关。所以，对于上述原始信号分解所得的IMF分量，需选择互相关准则消除伪IMF分量，即通过计算各IMF分量与原始信号的互相关系数，将互相关系数较小的IMF分量予以去除。对于1号裂纹缺陷与2号未熔合缺陷的互相关系数计算结果如表2所示，由于微弱相关要求相关系数的值在0～0.3之间，低度相关要求相关系数的值在0.3～0.5之间，显著相关要求相关系数的值在0.5～0.8之间，高度相关要求相关系数的值在0.8～1之间，所以对于裂纹缺陷信号而言，应去除第4阶与第7阶的本证模态函数；对于未熔合缺陷信号，应去除第2阶、第7阶与第8阶的本征模态函数，然后再通过剩余的IMF分量对缺陷信号进行重构，从而得到去噪后的超声回波信号。

表2 各IMF分量的相关系数

在通过信号重构后，可以得出重构后的裂纹信号与原始裂纹信号的相关系数为0.82，重构后的未熔合信号与原

始未熔合信号的相关系数为0.89，该数据说明它们高度相关，因此可选择重构后的信号代替原始信号。计算得到缺陷信号重构结果如图6所示，根据信噪比(SNR，signal noise ratio)以及均方差(MSE)性能的评价方法，分析重构结果见表3，从表中数据可以看出该方法对于2号未熔合缺陷有着较高的信噪比与较低的均方差，对于1号裂纹缺陷信号这种较为复杂的信号重构效果不佳。

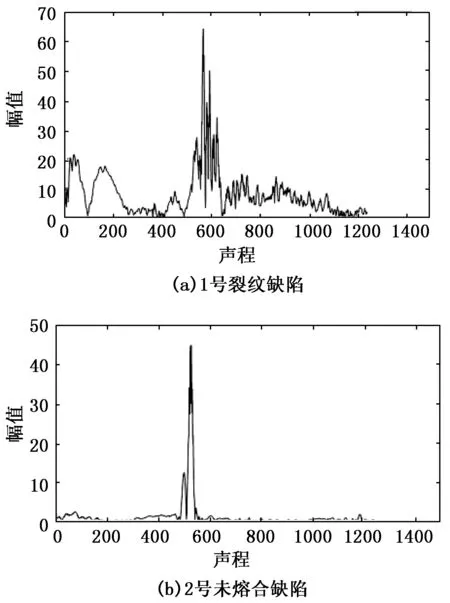
图6 缺陷信号重构结果

表3 缺陷信号重构结果

4 基于小波去噪的EMD算法

EMD方法相比于传统的时频分析方法具有许多独特的优点，但是由于其自身发展的不成熟，所以在实际应用的过程中存在着各种不同的问题。基于此，本文将该方法与小波分析相结合，旨在通过理论与应用都较为成熟的小波分析来改善EMD方法的应用效果，所以提出了基于小波去噪的EMD算法。

4.1 基于小波分析的信号消噪

由于超声A扫的数据量不大，所以本文采用db小波对信号进行分解重构，采用的评价方法与上文所述EMD分解的方法保持一致，即采用信噪比与均方差来评价信号重构结果。首先分别对1号裂纹缺陷处的A扫信号按不同阶数和分层近似系数进行重建，得到如图7的 SNR 和 MSE 比较图，从而选择去噪效果好的db小波阶数。

图7 db1～db9 重构图像

从图7中可以看出，对原始1号裂纹缺陷的A扫信号进行db8小波的3层近似系数进行重构，能够得到的SNR值及MSE值较为合理，其中MSE的值1.836 1、SNR的值为13.999 8。所以本文对1号裂纹缺陷与2号未熔合缺陷的A扫信号按db8进行分解，并且基于第3层近似系数重构，得到结果如图8所示。

图8 信号db8分层小波重构

然后本文在主要使用db小波三层分解A扫信号的情况下，再通过信号处理对A扫信号进行去噪使得曲线变得更加光滑。去噪方法主要包括强制去噪、默认阈值去噪和给定软阈值去噪这3种方法，本文由 db1～db9 小波分别选择这3种方法来重构原始1号裂纹缺陷的信号，得到SNR与MSE的对比图如图9所示，从图中可看出对于该信号，3种消噪方法中默认阈值消噪有较高的信噪比、较低的均方差，强制消噪受小波函数基的影响比较大，默认阈值消噪与给定阈值消噪这两种方法与小波函数基关系不大。

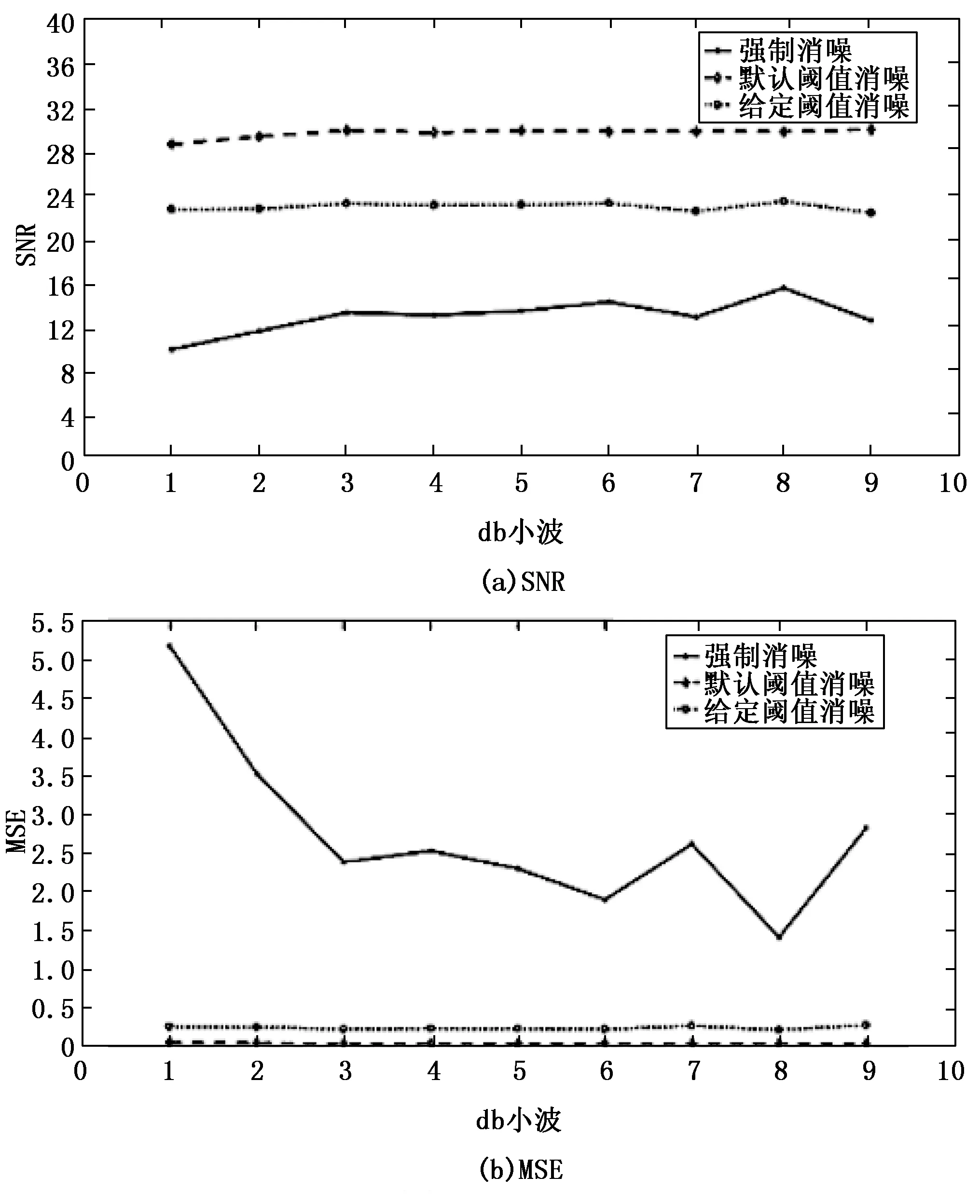
图9 db1～db9按3层分解的比较图

在此基础上，为了与小波重构比较效果，按db8小波画出1号裂纹缺陷信号与2号未熔合缺陷信号的采取3种不同的去噪算法从而得到的结果如图10所示。

图10 3种消噪方法比较

4.2 去噪信号的EMD分解

在通过小波分析对于缺陷信号进行初步的去噪之后，对于去噪后的信号再进行EMD分解，与含噪声信号的分解结果相比，分量明显减少，1号裂纹信号仅分解6个分量，2号未熔合信号仅分解7个分量。然后与上文所述相同，通过互相关准则计算各个IMF分量的相关系数，从而避免了IMF分量选择的盲目性，得到结果如表4所示。

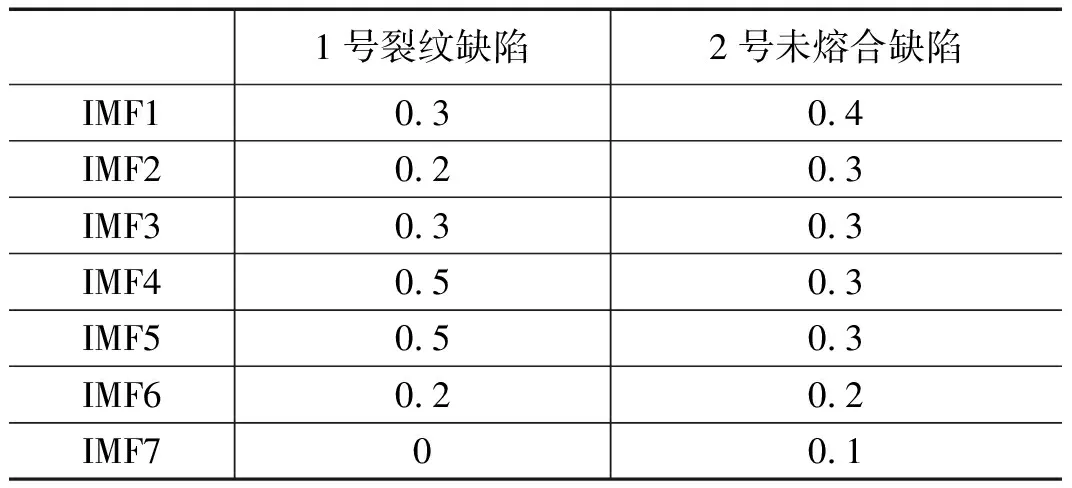
表4 各IMF分量的相关系数

1号裂纹缺陷信号选择IMF1、IMF3、IMF4及IMF5分量对信号进行重构，2号未熔合缺陷信号选择IMF1～IMF5分量对信号进行重构，得到重构结果如图11所示。通过对比上文所述的EMD分解重构结果，见表5，可以发现基于小波去噪的EMD分解重构有较高的信噪比与较低的均方差，重构效果更好。

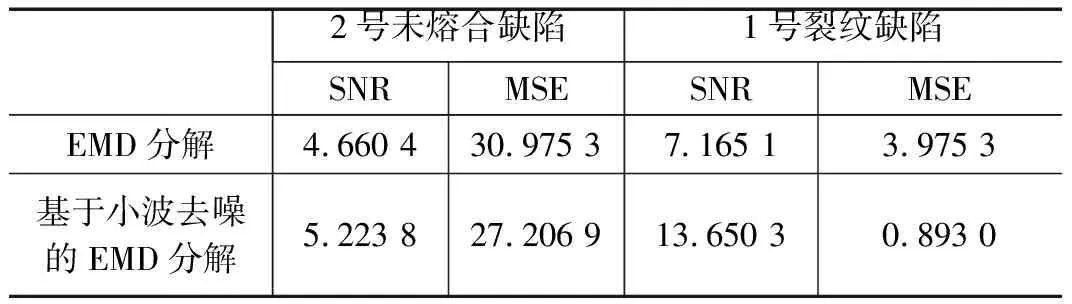
表5 缺陷信号的SNR与MSE

图11 缺陷信号重构结果

5 结束语

本文首先针对接管角焊缝的结构特点，制作相应试样，

完成超声相控阵检测试验，得到试样的检测结果，主要分析1号裂纹缺陷与2号未熔合缺陷这两个缺陷的检测结果。在此基础上通过EMD算法完成分别对这两个缺陷信号进行分解与重构，得到相应的重构结果，通过均方差与信噪比来评价其重构结果。最后提出小波降噪和EMD 分解相结合的降噪方法，该方法将小波去噪后的信号再进行EMD分解与重构，其降噪能力相比传统算法效果显著提高，降噪后重构的信号信噪比和均方误差得到优化，缺陷回波信号测量的效果更好，有利于缺陷的B扫成像效果，从而提高缺陷的检出率。