基于组合波工程化测量消除引线互感的接地阻抗测量方法

张 云，李 谦，胡晓晖，肖 云

(1.广东电网有限责任公司 惠州供电局，广东 惠州 516003；2.广东电网有限责任公司 电力科学研究院，广州 510080；3.武汉市康达电气有限公司，武汉 430070)

0 引言

随着电网向特高压、大容量和远距离方面的发展，电力系统的安全运行日益重要，为了提高电网的可靠性保证正常供电，变电站接地装置对于保证电力系统的可靠运行起至关重要的作用[1-2]。接地参数测量是电力系统接地工程竣工验收的重要环节。接地测量值的准确与否关系到电力工程能否如期投运，以及后期是否需要采取降阻措施以改善接地参数。变电站接地阻抗测量中，由于试验方法和地形的局限性，电压线和电流线的布线经常并行，电流线与电压线之间的互感耦合是不可避免[3-4]且不可忽略的[5-6]。

对于接地阻抗测试中的互感耦合影响研究由来已久，对其做过很多试验与研究。除了现场采取注意电流线电压线放线方式上尽量远离避免互感影响外，学者们还提出了不同的方法[7-11]。公式补偿法[12]通过构建电流线电压线的互感计算模型，通过土壤电阻率可以计算出由于互感耦合引起的电阻分量实部误差以及电抗分量虚部误差，但该方法不具备现场操作性。由于现场环境复杂多样，土壤分布不均匀，实际土壤电阻率无法准确测量估算，导致估算的互感抗误差比较大，甚至会出现互感分量估算值大于感抗分量测量值的情况。

另有基于异频法测量值修正的方法[13]，通过观察每次移动后不同位置时测量值的变化，即可得到单位长度对应的电压线和电流线之间的互感变化量。用测试点对应的电感量减去互感变化量与并线长度的乘积，即可得地网自感抗。此方法的一个前提条件是异频法测量的接地阻抗实部R不受互感耦合影响。由于异频法测试仪使用交流正弦电流作为激励信号，且测试仪的直接测量值为电流幅值Im、电压幅值Um以及电流电压之间的相角θ，因此接地阻抗模值Z、实部R和虚部X都是通过电压、电流幅值和相角间接计算得到的。基于以上测量原理，测试线间的互感耦合分量M不仅会引起电压测量误差ΔU，还会引起相角测量误差Δθ，所以间接计算的阻抗模值Z、实部R和虚部X都会含有与互感M相关的误差，导致基于异频测量值修正的方法在现场并不可行。

因而，如何在测量方法中剔除互感成分，真实保留接地网接地阻抗电感分量，并获得接地阻抗准确结果，成为迫切需要解决的问题。

针对以上问题，本文提出了基于组合波的工程化测量方法解决互感耦合分量对接地阻抗测量结果的影响。首先向接地网施加方波电流激励，以克服互感耦合影响准确获得接地阻抗阻性分量测量值R。然后向接地网施加正弦波电流激励获得接地阻抗模值测量值Z，并计算得到含有互感耦合分量的接地阻抗的感抗分量X。在测量现场改变电压线和电流线并行距离，得到在不同互感耦合强度情况下的组合波接地阻抗测量值，并建立测量值与测试线并行长度的方程组，解析剔除互感耦合分量，即可得到接地网接地阻抗的准确测量值。仿真计算及现场测试结果表明，本文提出的基于组合波的工程化测量方法能准确地获得不受互感耦合影响的接地阻抗测量值，对提高电力系统的安全运行水平具有重要的理论和工程意义。

1 基于组合波消除互感分量的接地阻抗测量方法

1.1 基于组合波的接地阻抗测量方法

目前常用的接地阻抗测量方法，无论是工频法还是异频法均使用正弦波电流作为激励信号，当现场电流线电压线平行共线有互感耦合时不可避免会产生测量误差。为避免互感耦合的影响，《DL/T 475-2017 接地装置特性参数测量导则》[14]推荐使用交变直流的方波电流测量土壤电阻率，特别是测量深层土壤时，电流线和电压线平行共线距离可长达数百米，使用方波电流可以有效克服互感耦合对接地电阻测量的影响。

方波电流不仅可以用来测量土壤电阻率的视在接地电阻，而且研究表明[15]，用在工频附近频率的方波电流测量的电阻值与工频接地阻抗的实部是等效的。基于此思路，本文提出基于方波和正弦波的组合波电流测量接地网接地阻抗的方法。该方法按一定顺序给接地网注入交变直流的方波电流和异频正弦波电流，首先在方波电流激励下持续一段时间，测量响应电压的稳态信号，从而计算得到接地阻抗的电阻分量测量值R；然后在正弦波电流激励下持续一段时间，测量相应电压的稳态信号，从而计算得到接地阻抗的模值Z；最后基于接地阻抗的电阻分量和模值，计算得到接地阻抗的电抗分量X和相角θ。基于组合波的接地阻抗测量流程如图1所示。

图1 基于组合波的接地阻抗测量流程

此方法与异频法的差异在于，接地阻抗参数中独立测量值是接地阻抗电阻分量R和接地阻抗模值Z，由于电阻分量是基于方波电流测量得到的，从原理上不受现场互感耦合的影响，可以保证接地电阻分量测量是准确的。进一步，接地阻抗的模值Z和电抗分量X测量值中虽然包含互感耦合分量，但由于R测量值不受互感耦合分量影响，可以建立互感耦合分量与现场共线距离的关系，为从接地阻抗测量值中剔除互感耦合分量提供了一种可能性。

1.2 基于工程化测量消除互感耦合分量的方法

现场工程化测量消除互感耦合分量的方法如下：首先给接地网施加交变直流，可实现接地网接地阻抗的电阻性分量的准确测量。基于不受互感影响的参数R，再施加正弦波电流激励进行感性分量测量，通过改变多组电位线和电流线并行长度，得到测量响应，可获得到包含互感耦合分量和地网自感分量的接地阻抗模值测量值Z和感抗分量X。

感抗分量测量值X中包含接地网的自感抗和互感耦合分量。通过改变现场平行共线长度，可以建立感抗分量测量值与测试线平行共线距离的方程组。进一步对方程组解析，可以实现对感抗测量结果进行“拆解”，将互感耦合分量计算出来，从而得到剔除测量引线互感耦合影响的接地阻抗的真实值。工程化测量剔除互感耦合分量的接地阻抗测量原理示意图如图2所示。

图2 工程化剔除互感分量的接地阻抗测量示意图

基于组合波接地阻抗测量值剔除互感耦合分量的实施过程为：使用激励正弦波电流信号，可在电流极距离的0.618倍附近布置至少两个电压极，对应的两个测量点互感耦合强度不同且测试仪可分辨。在相同频率下，通过组合波测量接地阻抗可获得两个接地阻抗视在测量值Z1与Z2。通过Z和R，可以计算出接地阻抗视在测量值的电抗分量X1与X2，实际测量中得到接地阻抗的感抗分量X来源于两部分[16-17]，(1)地网接地阻抗本身的电感分量XL(Ω)；(2)电压、电流引线的平行互感XM(Ω)，则有：

X1=XL1+XM1

(1)

X2=XL2+XM2

(2)

由平行共线引起的单位长度的电感分量为[18]：

(3)

由于两个电压极距离不远，从布线的整体区域来看，电压线、电流线的等效间隔距离d基本不变，两个测量点对应的整体等效土壤电阻率ρ基本不变，测量的频率f不变，ΔXM可简化为一个常数。设电压极与电流极平行共线距离l1、l2，则有:

XM1=ΔXM·l1

(4)

XM2=ΔXM·l2

(5)

自感抗与接地网的拓扑结构相关，不受布线距离影响，是个常量，则有：

XL1=XL2

(6)

而互感耦合分量则随测试线并行长度呈线性函数关系，因此，互感耦合分量XM1，XM2与电压极与电流极平行共线距离l1、l2成正比，则有：

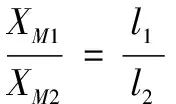
(7)

综上得到解析剔除互感耦合的方程组如下：

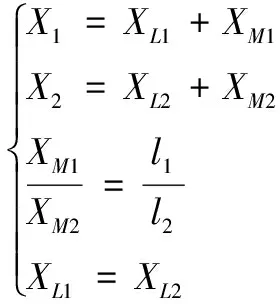
(8)

通过解析计算得到接地网互感抗XM1，XM2以及自感抗XL。

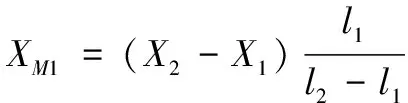
(9)

(10)

(11)

不受互感耦合影响的接地阻抗的电阻分量为RG=(RG1+RG2)/2。最终便可计算得到剔除互感耦合分量的接地阻抗测量值ZG。

ZG=RG+XL

(12)

2 变电站现场测量案例

2.1 测量方案

为了验证基于组合波法的接地阻抗测试仪实测变电站接地网的有效性，以及基于组合波工程化测量方法剔除接地阻抗互感耦合分量的有效性，在某新建110 kV变电站进行了接地网接地阻抗的现场对比测试。测量依据为《DL/T 475-2017 接地装置特性参数测量导则》，对比测试的设备是基于组合波法研制的接地阻抗测试仪和澳大利亚红相8 000接地阻抗测量系统。

该110 kV变电站是即将投产的室内GIS变电站，占地面积小，主体建筑均有自身的接地网，各接地网互相连接，构成变电站的接地网系统，根据变电站的卫星定位得出，110 kV变电站地网对角线长度为80 m。变电站的线路尚未进入变电站，无需考虑避雷线分流的影响。为了降低变电站接地阻抗，从变电站内往外打了数口斜井。考虑到斜井增大了地网对角线，相应地增大布线距离，为简化试验，暂时将斜井断开。

变电站外是一大片已经完成平整的工厂用空地，土壤较为均匀。为了验证测量接地阻抗的准确性，采用了30°夹角法和远离夹角法两种布线方法。场外空地最远点的距离变电站边缘为300 m，是变电站主接地网对角线的3倍，将电流极、电压极布置在此片空地满足30°夹角法的布线要求。另外，为了验证互感耦合对实际测量的影响，在空旷的场地上通过人为布置不同耦合强度的的测试线，可以获得不同共线距离下接地阻抗和互感分量的定量测量数据，并验证通过工程化测量消除互感耦合分量方法的效果。具体布线方案如图3所示。

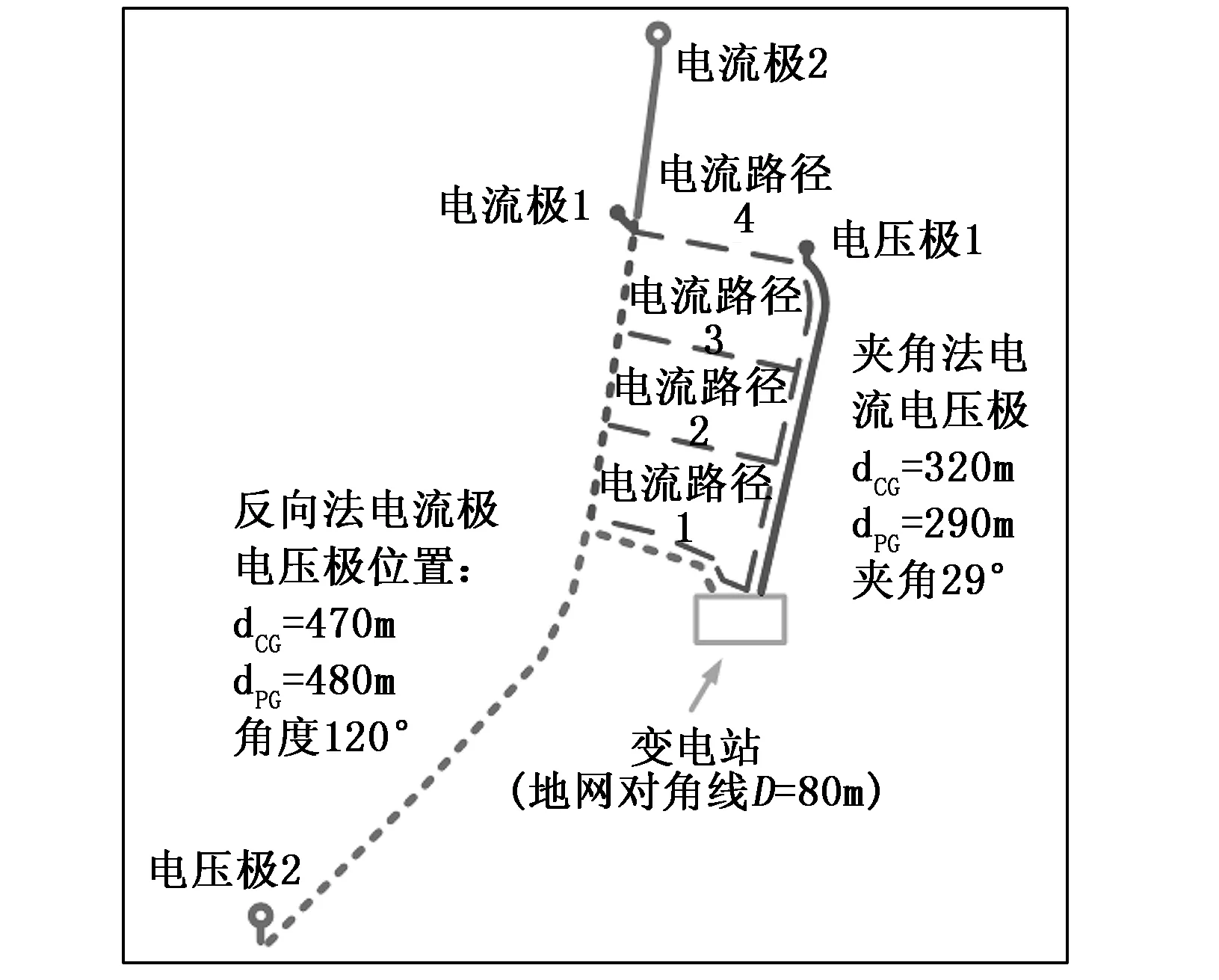
图3 某变电站接地网测试布线路径示意图

30°夹角法的电压极布置在变电站正对面场地边缘的电压极1位置，电压线沿为变电站到电压极1的实线路经布置。30°夹角法的电流极布置在场地靠近路边的电流极1位置。为了避免互感耦合的影响，电流线从变电站出去之后，沿红虚线所示的电流路径1布置。通过GPS测绘，电流极1距离变电站320 m，电压极1距离变电站290 m，实际夹角为29°，满足布线要求。

远离夹角法的电流极为电流极2位置，电流线沿电流路径4布置，电压极位置为电压极2，电压线沿密虚线路径布置。通过GPS测绘，远离夹角法的电流极2距离变电站470 m，电压极2距离变电站480 m，为地网对角线的6倍，实际夹角为120°，满足布线要求。

基于30°夹角法的电流极1和电压极2，除了电流路径1之外，还布置了电流路径2、3、4。电流路径1与电压路径先垂直，再远距离平行，可以认为无互感耦合，电流路径2～4分别与电压路径平行一段距离，再垂直远离至与电流路径1融合。通过GPS测绘，电流路径1～4与电压路径平行的距离分别为0 m，126 m，200 m，300 m。电流线与电压线间隔距离为2 m左右。

2.2 接地阻抗测量数据分析

按以上方案完成现场布线后，使用异频法红相测试仪和基于组合波的接地阻抗测试仪变换不同电流电压极和测试线路径对变电站接地网接地阻抗进行了测试。异频法和组合波法测试仪现场试验电流均为3A，测量数据如表1所示。

表1 接地阻抗现场测量数据

首先分析30°夹角法情况下异频法和组合波法的测量数据。电流路径1对应是没有互感耦合的情况，可以看到异频法与组合波法对应的R，X，Z，θ等测量数据是一样的。说明在没有互感耦合情况下，组合波法测试仪的测量数据与异频法是等效的，30°夹角法对应的接地网无互感耦合影响的测量值为Z1=0.752+j0.020=0.752∠1.5°。随着电流路径中平行共线距离的增加，异频法测试仪测量数据中R和Z有少许增加，R增加了20 mΩ，并且在不同频率下异频法测量的R并不完全相同；Z增加了31 mΩ，X增加的幅度比较大，从20 mΩ增加到129 mΩ；θ从1.5°增加到9.5°。现场测量数据印证了互感耦合对异频法测试仪阻抗各分量都有影响，而且对阻抗虚部X影响最大。对于组合波法测试仪，测量数据中R在4种路径下几乎无变化，说明使用方波测量接地阻抗的实部的确可以不受互感耦合影响。组合波法使用正弦波测量的X、Z值与异频法测量数据基本一致，测量的阻抗相角比异频法偏大一点，这是因为组合波法测量值的实部比异频法实部小所致。通过以上数据分析可以看到，在不同互感耦合强度情况下，基于组合波的接地阻抗测量值实部不受互感耦合影响，但是异频法测量值的所有阻抗分量都会受互感耦合影响，尤其是感抗部分增加幅度最大。以上现象与理论分析是一致的。

再分析远离夹角法测量数据。由于远离夹角法布线路径避免了互感耦合影响，组合波法测量值与异频法测量值一致，Z2=0.650+j0.019=0.650∠1.7°。依据DL/T 475测量导则，远离夹角法测量数据需要用公式(13)进行补偿换算得到修正之后的接地阻抗测量值。远离夹角法的电流极2距离变电站470 m，电压极2距离变电站480 m，夹角为120°，带入公式(13)可以计算得到修正系数为0.885。

Z=

(13)

修正之后的远离夹角法接地阻抗测量值为Z2’=0.734 Ω。此修正值与30°夹角法测量值(Z1=0.752 Ω)相差仅为2.4%，说明本次接地阻抗现场布线合理，测量值也是可信赖的。

2.3 接地阻抗仿真对比分析

为了进一步研究接地阻抗测量值的准确性，将测量数据与变电站接地阻抗理论计算值进行对比分析。

对变电站周围不同深度的土壤电阻率进行了测试。考虑空置场地的最大尺寸只有300 m，温纳四极法的最大测量间距取为100 m。这个测量间距，与接地网尺寸(对角线长度80 m)相当，满足反映深层土壤结构的要求。土壤电阻率测量结果见表2。根据表2的实测结果，利用CDEGS软件进行土壤反演仿真。由于变电站较小，而且周围土壤较为均匀，使用水平分层模型进行土壤电阻反演，发现变电站场区土壤可以用4层水平分层土壤来描述，仿真结果详见表3。

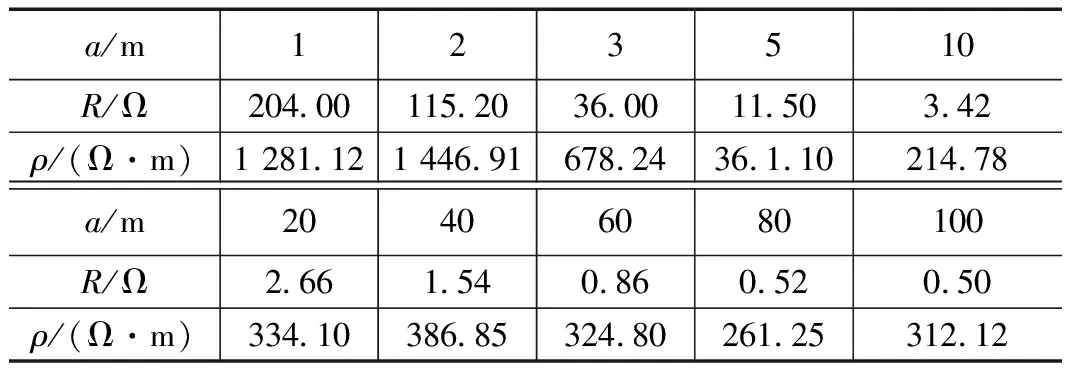
表2 土壤电阻率测量数据

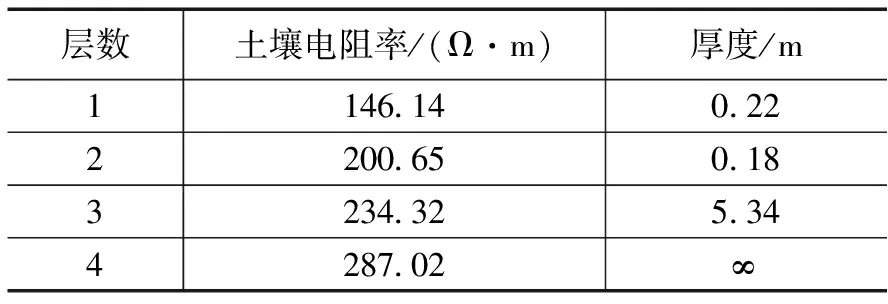
表3 水平多层土壤反演值

根据接地网设计图纸以及斜井施工图斜井虽然未与变电站接地网直接相连，但由于斜井与接地网之间存在土壤，也会对地网散流起到一些作用。接地网设计图如图4所示，考虑斜井的接地网CDEGS模型如图5所示。接地网长度为74 m，宽度为40 m，以水平接地体为主，以垂直接地体为辅组成复合主接地网。水平接地网采用150 mm2铜绞线，以约5.5 m×5.5 m方格敷设，水平接地网埋深离地面-0.8 m，垂直接地极为铜镀锌钢棒，顶部埋深为-0.8 m。

图4 接地网设计图

图5 CDEGS软件中的接地网模型

将土壤电阻率反演结果代入接地网仿真模型进行计算，得到该变电站接地阻抗的仿真结果为：接地电阻Z=0.765 Ω，相角θ=2.1°与实测数据Z= 0.752 Ω，相角θ=1.5°非常接近，相对误差为1%，说明了无互感情况下基于组合波法的接地阻抗测量值是准确的。

3 变电站场区互感耦合实测数据与仿真与分析

3.1 基于工程化测量值的互感分量计算与剔除

本文在第1节提出了基于组合波的互感耦合分量工程化测量与剔除方法，本节利用变电站现场基于组合波法的实测数据进行分析，获得互感耦合分量和接地阻抗的实测值。

基于组合波法在不同电流路径情况下的测量数据，可以用感抗分量X的变化计算得到实测的互感耦合分量。电流路径1对应无互感耦合，电流路径2～4互感耦合逐渐增加，则对应X测量值的增量即为实测的互感耦合分量XM，再除以平行共线距离l可以得到互感耦合系数。相关数据见表4。

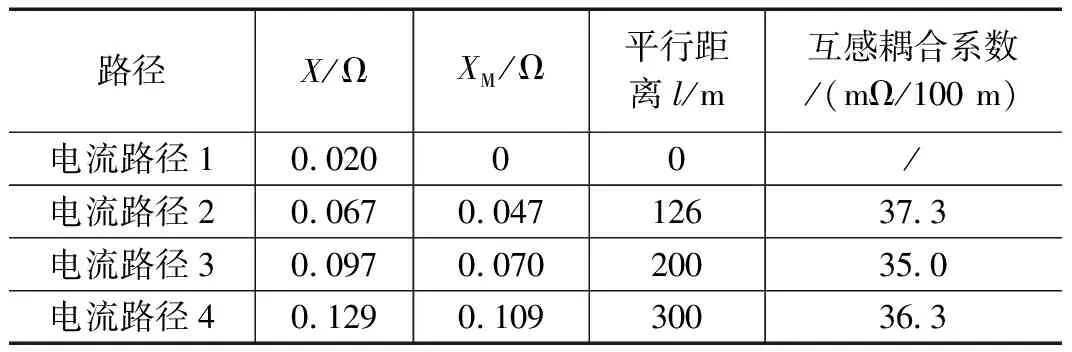
表4 实测互感耦合值

从表4数据可以看到，现场单位长度的引线互感耦合系数为36～38 mΩ/100 m，基本上呈现为一个固定值。

假设现场互感耦合无法避免，布线只能按路径2～4实施，那么基于组合波测量值和公式(9)～(11)可以计算任意两个测量点的接地阻抗和互感耦合系数。当测量点为3个或者更多时，可以基于多点测量数据进行线性拟合得到更准确的互感耦合系数。基于本次测试的3个布线路径，将对应路径的感抗分量测量值与平行共线距离进行线性拟合，可以得到如图6所示的拟合结果。线性拟合参数的增益值为互感耦合系数，为0.354 mΩ/m，初始值即为剔除互感后的地网自感分量X=23.7 mΩ。

图6 感抗分量测量值线性拟合

基于3个路径的实部测量值，可以得到接地电阻分量均值为R=0.753 Ω。因此，基于组合波工程化测量的接地阻抗测量值为Z=0.753+j0.0237=0.753∠1.8°。此数据与路径1无互感情况下的测量值几乎一致，说明基于组合波工程化测量方法可以有效剔除测量值中的互感耦合分量，提高接地阻抗测量的准确性。

3.2 基于仿真的互感耦合分量对比分析

使用CDEGS可以建立考虑引线互感耦合的接地阻抗测量模型。在辅助电极布置位置采用0.5 m长的等效短导体模拟电极接地极，采用地表上的绝缘导线模拟电极引线，电流线将注流导体和电流极连通形成回路，注流导体和电流极分别注入±3 A的电流，电压线将电压极连接至距离注流导体水平间隔0.5 m处的位置，因电压表内阻非常大，直接选择将电压线端点悬空模拟通过高内阻电压表与注流导线连接。电流线和电压线之间在靠近部分的平行段间距取为2 m。

以夹角法中的电流路径1布线方案为例，读取注流点导体和悬空导体的电位值，以两者做差并除以测试电流值，即可计算得到接地阻抗测量值。其中接地阻抗测量值的虚部X包括地网接地阻抗本身的电感分量XL和电压、电流引线的平行互感分量XM，用该虚部值减去接地阻抗计算值的虚部，即可得到电压、电流引线的互感耦合仿真计算值。考虑实际布线长度和互感耦合的仿真模型，如图7所示。最终可以得到不同布线方案下接地阻抗测量仿真计算值，如表5所示。

图7 考虑互感耦合的CDEGS仿真模型

表5 互感分量仿真值

由表5中的仿真结果可以看到，路径1虽然电流线和电压线间隔距离比较远，但仍有14 mΩ的互感分量。路径2～4随着近间隔距离的平行共线长度增加，互感耦合分量显著增大，而且互感耦合分量与现场测量的互感耦合值非常接近。用路径2～4的互感抗值减去路径1的互感抗值除以平行共线长度，即可得到仿真的单位长度互感耦合系数，为26～28 mΩ/100 m的一个固定值。仿真的互感耦合系数比实测的互感耦合系数小约10 mΩ/100 m，也主要是因为路径1实测值处理为没有互感分量的原因。

从以上数据可以看到，实测和仿真的互感耦合数据变化规律相同，互感耦合系数相差不大，说明基于组合波法和共线距离测绘的工程化测量方法可以准确获得比较准确的场区真实互感耦合系数测量值。此方法可以省去对现场土壤电阻率分层测绘和复杂的反演计算，获得互感耦合定量测量值，再对接地阻抗视在测量值进行修正，即可实现消除互感耦合影响的接地阻抗准确测量值。

4 结束语

1)本文提出了一种基于组合波工程化测量消除引线互感的接地阻抗测量方法，首先利用交变直流方波激励，获得准确的不受互感影响的电阻分量数据，再用正弦波电流激励，获得含有互感耦合分量的接地阻抗模值，进而计算得到接地阻抗感抗分量和角度。在此基础上，通过构建不同耦合路径，实现接地阻抗值和互感耦合系数的工程化测量，通过方程组解析可从现场测量值中分离出互感耦合分量与地网感抗分量，获得接地网接地阻抗真实值。

2)通过现场与异频法对比试验，采用30°夹角法与远离夹角法测量的接地阻抗误差为2.4%；基于变电站实测的土壤电阻率和土壤分层反演，在CDEGS软件中建模，仿真计算得到接地阻抗值与实测数据误差仅为1%，说明基于组合波的接地阻抗测量方法是准确有效的。进一步基于现场布线路径在CDEGS软件中建立互感耦合模型，互感耦合系数仿真计算值和实测值误差为10 mΩ/100 m，进一步说明基于组合波的工程化测量方法能很好的将现场实际互感耦合系数定量测量出来，并可将互感耦合分量从接地阻抗测量值中剔除，大幅提高了接地阻抗测量的准确性。