面向城市主通道的信号协调控制优化研究

王逸凡， 王雪雪， 还 斌

(上海电科智能系统股份有限公司， 上海 200063)

0 引言

随着社会经济的发展和城镇化进程的加快，机动车保有量急剧增加，居民的出行需求也在持续扩大，导致城市交通拥堵现象已成为一种常态. 缓解城市交通拥堵问题一般可通过新建基础设施或优化城市交通管理2种方法[1]，但是由于新建道路受到资金和土地资源的制约，在工程中普遍希望通过交通控制或交通诱导等手段来实现路网中交通流的合理分配，从管理的角度减少交通拥堵的发生.

交通控制是近年来受到行业内广泛关注的领域，也是解决交通拥堵问题最为直接的方法之一. 目前路网中干线的信号协调控制是减少主干道延误、提高其通行效率的有效手段，国内外众多学者也在这个方面有了比较深入的研究. 李林[2]提出了传统MAXBAND模型在实际应用中存在的问题，并进一步研究了不同饱和状态下的连续流控制方法. 田秀娟[3]在考虑车辆到达与消散的条件下，提出以延误最小为目标的干线协调控制模型并用自适应粒子群算法进行求解验证. 郑献予[4]综合参考传统干线协调方法与多智能体系统，提出了以关键交叉口为中心的干线动态协调控制方法. 何忠贺等[5]通过建立车辆延误与绿波带宽间的线性关系，采用动态规划求解实现了在损失一部分绿波带宽的情况下保证延误尽可能小的目标. 郑丹云[6]提出了一种系统通行量最大的干线绿波协调方法，可提高通过车辆数并在一定程度上优化停车次数与延误时间. Yang Xinwu等[7]通过引入最小生成树聚类的思想优化了传统遗传算法，并将其应用于干线协调控制模型中，减少了总延误时间. Elise van der Pol[8]等结合深度Q学习和干线协调方法，在新奖励机制的基础上实现了信号协调控制，相比早期的强化学习算法进一步优化了干线的行程时间.

上述研究虽然都在传统干线协调方法的基础上进行了一定程度的优化，但大都还是基于固定干线的协调. 在城市路网中，有一部分路段承载着路网中主要交通流，按照交通流向将这些路段连接形成的路径称之为城市主通道[9]. 不同于传统干线的概念，城市主通道会随时间的变化而变化，并且具有方向性. 本文的研究能从交通供给和需求的角度出发，通过对路网中一部分关键道路的优化，实现日常模式下车辆快速通行的效果，改善现有城市主要通道的交通拥堵问题.

此外，虽然有学者近年来提出过一些比较新的概念，但是这些数据和方法大都还处于实验阶段，不具备实际应用的条件. 如Jiarong Yao等[10]基于车辆采样轨迹数据和冲击波理论估计车辆达到信息和排队状态，建立了双向总延误最小为目标的协调控制模型，但是车辆轨迹目前难以精确获取且样本误差对模型的影响较大，可靠性及普适性较低. 本文的研究基于路网中各交叉口已建设备采集的多源数据，实时对交叉口的饱和状态、排队消散时间和各路段的车速特征等进行计算，可使改进模型的协调效果更符合实际的交通状况，适用于复杂的路网环境.

1 协调相位及其饱和状态判别

由于城市主通道具有方向性，通过其方向可确定经过每个交叉口时的转向情况. 结合各交叉口信号灯组的功能以及各交叉口信号灯组与其相位的关联关系，可实现对主通道中每个交叉口的协调相位进行自动化判别. 一般情况下，信号协调控制应考虑双向的情况，所以协调相位也应该同时对2个方向进行判别[11].

协调相位的饱和状态关系到相应的协调策略. 本文综合了时间饱和系数和空间饱和系数2个方面对协调相位的饱和状态进行综合判别. 其中，空间饱和系数根据协调相位的平均排队长度计算得到；时间饱和系数根据协调相位的平均时间饱和度计算得到.

协调相位饱和状态判别分为以下几个步骤：

步骤1根据上、下游交叉口的视频过车数据，计算下游交叉口的车道排队长度(指单信号周期内的排队长度)，采用式(1)：

(1)

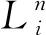
为简化计算，式(1)假设交叉口进口道均无拓宽的情况，在后续的研究中会考虑增加排队长度检测器等方法来进一步提高数据的准确性.

步骤2将单信号周期内的车道排队长度计算结果转换为协调相位的平均排队长度，将其与最大可容纳排队长度的比值作为空间饱和系数，其中最大可容纳排队长度参考路段长度与防止排队溢出预留的安全长度得到.

步骤3计算协调相位关联所有车道的时间饱和度之和，将其与协调相位关联车道数的比值作为时间饱和系数.

步骤4根据时间饱和度的计算原理，当交叉口上游越接近饱和状态时，交通流越不稳定，到达流量获取的准确性下降，此时空间饱和系数更能反映出当前协调相位的交通状况. 因此，在计算综合饱和系数时，考虑在越接近饱和状态时，空间饱和系数所占比重越大，反之则越小，采用式(2)

SC=SCS2+(1-SCS)SCT,0≤SCS≤1

(2)

式中，SC为综合饱和系数；SCS为空间饱和系数；SCT为时间饱和系数.

步骤5当综合饱和系数高于设定的阈值时，认为该交叉口的协调相位处于过饱和状态；当子区内同一主通道和方向上连续出现2个及以上交叉口的协调相位处于过饱和状态时，认为该子区内的这条主通道处于过饱和状态.

2 协调控制优化模型

综合考虑了目前在协调控制中一些常用的模型，本文在经典MULTIBAND模型的基础上进行改进，以适用于研究需求，具体改进的内容如下：

1) 根据交叉口的多源数据，实时地计算模型通用参数，而非采用原模型中的固定参数. 其中通用参数包含：各交叉口的排队消散时间和各路段的速度范围；

2) 修正了原模型中的约束条件，使其能实现双向绿初式绿波(绿波开始时间与第1个交叉口绿灯开始时间相同)，保证协调控制的整体效果；

3) 通过修改模型部分目标函数和约束条件，实现过饱和状态下的协调控制策略.

2.1 通用参数标定

1) 交叉口排队消散时间

根据第2节中计算的协调相位平均排队长度，计算交叉口排队消散时间，式(3)[12]：

(3)

2) 路段速度范围

基于上、下游交叉口的视频过车数据，计算单车经过路段的行程时间，通过设定的上、下限阈值确定行程时间的下限Tmin和上限Tmax. 计算路段速度范围，式(4)：

(4)

式中，e为路段速度下限；f为路段速度上限；d为路段长度.

2.2 协调控制优化模型建立

为简化流程，本文仅考虑双向均采用对称式相序配置，即正向和反向的相位放行时间偏差量Δ=0的情况. 经典MULTIBAND模型如下所示[13]：

(5)

(6)

(7)

(8)

(9)

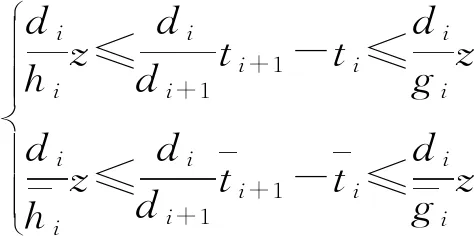
(10)

(11)

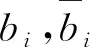
如图1所示(浅色为正向绿波，深色为反向绿波)，双向绿初式绿波可在第1个和最后1个交叉口绿灯启亮时，使双向的第1辆车能带领一队长度为绿波带宽度的车流连续通过协调交叉口，进而优化协调效果[14]. 为使双向协调均能从绿灯初期开始，在原约束条件中新增以下约束：

(12)

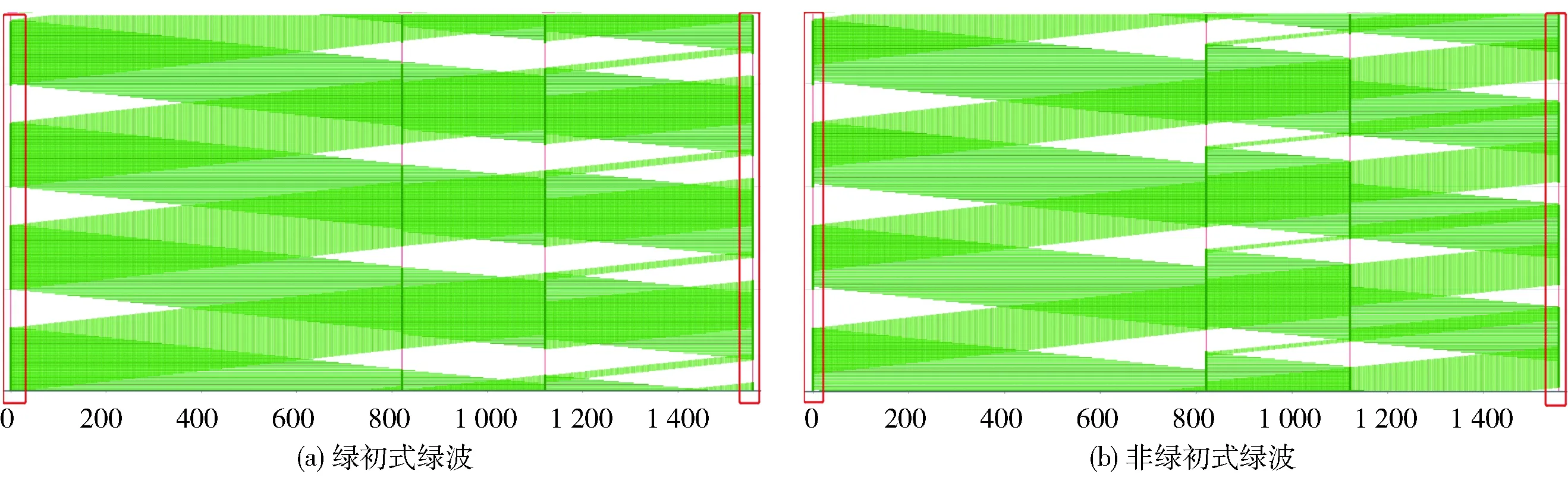
图1 绿波图

上述模型适用于未饱和状态下的信号协调控制，但是未饱和状态和过饱和状态下由于交通特性不同，因此也需要不同的控制策略. 针对过饱和状态，本文采用瓶颈交叉口上游红波控制截流、瓶颈交叉口下游绿波控制快速通行的策略，实现过饱和通道内慢进快出的协调效果. 此处将瓶颈交叉口定义为同一通道和方向上连续处于过饱状态交叉口中的第1个交叉口.

针对进行红波控制的路段i，当正向发生过饱和时，在原目标函数中，仅保留反向的绿波带宽权重，双向协调比例系数ki设置为1；当反向发生过饱和时，仅保留正向的绿波带宽权重，双向协调比例系数ki设置为0；其余约束条件与原来保持一致.

3 仿真实验

3.1 实验设计

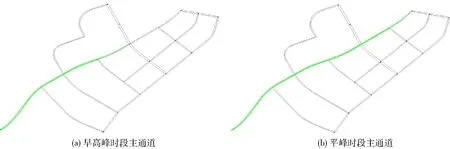
图2 主通道

本次仿真基于国内某城市20个连续交叉口所组成的区域，其中包含3条主干道和6条次干道. 区域内有学校、公园、住宅等交通发生和吸引源，日常的交通出行需求较高. 所有交叉口均采用SCATS控制系统，相位数从2～4个不等，且均为双向对称式放行方式. 输入的数据为这20个交叉口在2020年6月12日历史视频过车数据，包含设备编号、车辆信息(已脱敏)、经过时间、号牌颜色等参数，以及交叉口相位运行信息，包含交叉口编号、相位编号、相位开始与结束时间等参数.

已建立的协调控制优化模型属于混合整数线性规划(MILP)问题，因此采用分支定界法进行求解(Branch and Bound)，模型求解基于MATLAB 2019a平台，仿真实验基于VISSIM 10平台. 为了证明本文所述方法的有效性，仿真实验中同时对比了传统数解法与经典MULTIBAND模型的计算结果，同时通过主通道双向总延误和平均停车次数这2个指标来衡量协调方案的优势与合理性.

3.2 实验过程

首先在整个路网中根据交叉口的视频过车数据量确定每个时段的城市主通道，一般以小时为单位. 以2020-06-12早高峰时段08:00:00—09:00:00和平峰时段14:00:00—15:00:00为例，如图2所示.

根据第2节所述的方法分别对早高峰时段和平峰时段的主通道进行协调相位的饱和状态判别，然后根据判别结果按照第3节所述的方法分别建立协调控制优化模型.

基于MATLAB平台对已建立的协调控制优化模型进行参数求解，并通过求解的参数计算各交叉口之间的相对相位差.

将传统数解法、经典MULTIBAND模型与本文模型的协调参数计算结果分别输入到VISSIM中进行仿真实验，最终通过软件输出的主通道双向总延误和平均停车次数来对各协调方案进行对比评价.

3.3 实验结果

早高峰时段共涉及4个交叉口的协调控制，公共周期取120 s；平峰时段共涉及6个交叉口的协调控制，公共周期取73 s；各交叉口的绿信比方案通过等饱和度原则进行计算[15]，本文不做具体展开. 由于该路段中有1个交叉口的信号灯尚未启用，因此实际协调的交叉口数对比图2中少1个，具体的相位差方案结果如表1所示.

将表1中相位差方案分别输入VISSIM中测试运行. 为了避免随机误差对结果产生的影响，均测试3次后取平均值的方法，得到的输出指标如表2所示：

表1 3种模型的相位差方案从第1个交叉口开始 s

表2 3种模型的输出指标

仿真结果可看出：本文提出的改进模型在主通道双向总延误方面相较于传统数解法分别降低了26.06%(早高峰时段)和25%(平峰时段)，相较于经典MULTIBAND模型分别降低了11.76%(早高峰时段)和13.25%(平峰时段)；在平均停车次数方面相较于传统数解法分别减少了28.36%(早高峰时段)和35.71%(平峰时段)，相较于经典MULTIBAND模型分别减少了10.56%(早高峰时段)和20.59%(平峰时段).

综上所述，本文提出的信号协调控制优化方法能有效地对城市主通道进行协调控制，并且与传统干线协调模型相比能达到更好的协调效果. 此外，由于模型中还考虑了过饱和情况下的协调策略，因此相比以往仅适用于未饱和情况的协调控制模型具有更好的应用普适性.

4 结束语

本文首先根据主通道的基本信息和交叉口的视频过车数据，对协调相位及其饱和状态进行实时判别；随后在经典MULTIBAND模型的基础上，进行了实时计算模型通用参数、双向绿初式绿波设计和过饱和状态下的协调策略等方面的改进；最后通过MATLAB软件对建立的协调控制优化模型进行求解并在VISSIM平台上与传统数解法和经典MULTIBAND模型生成的协调方案进行了仿真对比，验证了本文所述模型的合理性和有效性. 相比于传统模型，本文提出的改进模型更多地从交通供需的角度出发来看待信号协调优化问题，同时结合了绿初式绿波的优点，并且充分考虑了交叉口当前的交通状况，优化了传统模型在实际应用过程中协调效果不佳的问题. 由于本文所提出的模型目前仅考虑了双向均采用对称式相序配置的情况，为提高其对于复杂相位交叉口的协调效果，后续可进一步研究在搭接相位等情况下的协调控制优化.