多点协同动态散斑的统计特性

车东博，王挺峰，张 绍，韩 越，李远洋

（1.中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033；2.中国科学院大学, 北京 100049）

1 引 言

激光散斑在医学，生物学，工程学，物理学和许多其他领域中都有广泛应用[1-5]。散斑强度在短期和长期内的波动以及空间相关性携带了随机介质的内部结构或目标靶面的光斑信息。在工业生产和国防领域实现激光的定向能量传输，监视远场目标靶面的激光能量密度中具有重要的作用[6]。在以往的研究中，通常采用望远系统[7]、桶中功率[8]和回波散斑[9]等方法获得反馈因子实现对目标光斑的去接触测评。望远系统对远场光斑成像，可以通过计算环围能量、平均半径等参数作为评价因子，但是这种方法受限于探测距离和相机帧频，也难以探测运动目标。以目标光斑的桶中功率作为反馈因子被广泛应用于自适应光束控制的闭环系统中，然而也存在着目标光斑监视范围小的弊端，尤其是针对目标在环系统中的非合作目标。相比回波散斑相位信息[10-11]，散斑的光强统计特性[12-13]可以无接触探测远距离的运动目标，更适用于刑事侦查、无损检测和在线精密测量等领域。

早在上世纪80年代，Sawatari等人提出了利用激光散斑确定光学系统焦平面的方法[14]。借助散斑成像技术，空间散斑统计特性普遍应用于微小位移或震动测量中[15-16]，Skipetrov开展了随机噪声对激光散斑相关性的影响[17]，从而提高了散斑空间统计特性的应用价值。另一方面，通过扫描激光产生动态散斑，并在探测器前加入空间滤波器[18]，利用散斑的时间统计特性实现距离量的精准测量[19]。随后团队利用动态散斑时间统计特性，实现非接触式测量远距离粗糙目标的速度[20]。Voronstov等人通过单点探测器采样回波散斑光强起伏获得的时间统计特性作为评价远场光斑的反馈因子[21]，结合随机并行梯度下降算法（SPGD）算法[22]，实现了基于散斑控制远场光斑。目前为止，针对回波散斑对远场光斑反馈评价的研究大多集中于单独空间统计特性或单独时间统计特性的计算[23]，而少有联合两种统计特性对目标光斑能量分布进行探测的研究。动态散斑信号具有的随机性将导致信号参数波动大，因此系统带宽小、采样时间长和信号误差大等问题制约着散斑应用的发展。

为了融合散斑场的空间和时间统计特性，保证精度的同时增加采样效率，本文提出了多点协同探测的方法，拼接多空间位点散斑的时间波动信号。在第二部分，分析了动态散斑时间频谱带宽与目标光斑尺寸的理论关系和多通道采集的可行性。第三部分仿真分析单通道和多通道采集获得评价因子的方法和精度，第四部分通过实验验证了多点协同散斑反馈因子的正确性。最后对本文做出总结介绍。

2 动态散斑频谱法判断聚焦光斑尺寸

2.1 散斑场强度的空间、时间相关特性

通过移动目标在菲涅尔衍射区域生成了一组符合高斯分布的动态散斑强度图。将粗糙目标表面看作由N个散射元组成的粗糙平面（r', z = L），激光光束经粗糙表面漫反射后自由传输至观察平面（r, z = 0），在观察面干涉相长或干涉相消，产生的颗粒状光学图案即为散斑。因此，在观察平面某点的光强U(r,z= 0)是通过每个散射元中心漫反射得到的光场相干叠加。

其中，N为目标平面散射元的个数，Al为目标面上散射元的光场振幅，φl仅取决于目标粗糙平面的随机变量，且具有零均值和在[-π，π]区间内波动的特点。接收面上点的相位均值Фl由三部分组成，目标平面上散射元的出射波球面相位φlT；散射元从目标平面到接收平面的光程差kRl1；目标面到接收面的传输过程中所产生的相位畸变φlβ。

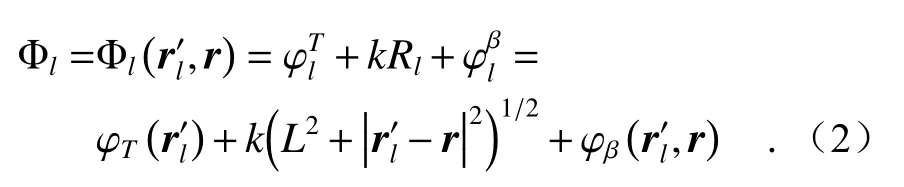
根据散斑场的统计特性可知，大量散射元以正常的速度随机移动会产生散斑图像的波动，移动的散射元和静止的散射元分别产生的散斑图是完全展开的，且符合高斯散斑的统计特性。由静止的散射点和运动的散射点分别引起的散斑图像相干性可以得到观察平面(r1,t)处的瞬时强度[24]。

其中，c为常数，c=k/(2πL)，目标面反射系数0＜γ(r') ＜1，且在平坦表面的延展目标靶面上γ(r')为常数。时刻间隔t内目标表面移动距离为|v|t，δs代表粗糙平面的散射元面积。{ηl}在统计上是独立的辅助随机变量，统计特性满足：

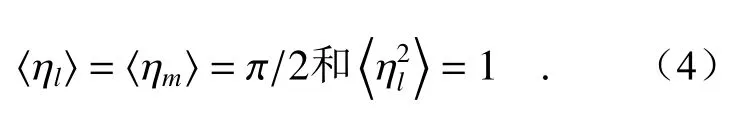
据S.M.Rytov[25]等人对散射效应的研究，采用小斜率近似将探测面的斑场平均强度用积分表示

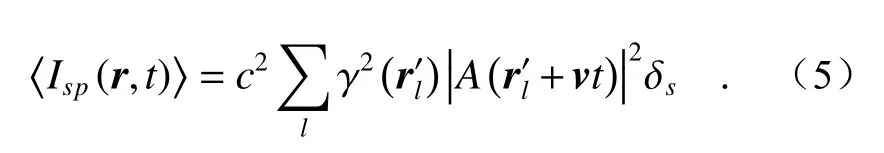
探测面(r1,z= 0,t)散射场的强度波动δIsp可用散斑场强度与平均值之间的偏差表示为

散斑强度波动的时间空间相关函数（mutual correlation function）定义为探测面(r1,t1)和(r2,t2)两点的强度波动的乘积，

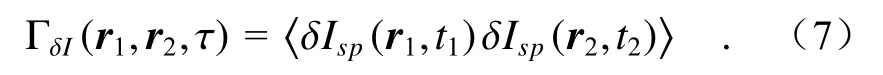
考虑到t1时刻和t2时刻间隔为τ，而η和φl中的φ仅取决于散射元内的表面粗糙度，不随粗糙面和观察点的移动而改变。因此假设η1=η2和φl1=φl2。则公式（7）可表示为

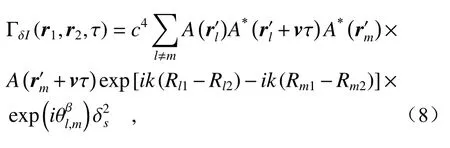
其中光束传输距离L远大于光束在目标平面与探测平面坐标系之间的偏移|r'-r|，因此光程产生的相位可使用泰勒级数展开，

ρ'= rm'-rl'代表目标平面坐标系；ρ = r2-r1代表探测面坐标系。假设目标照射面积内有足够数量的镜面反射点，则可用面积公式替代公式（8）

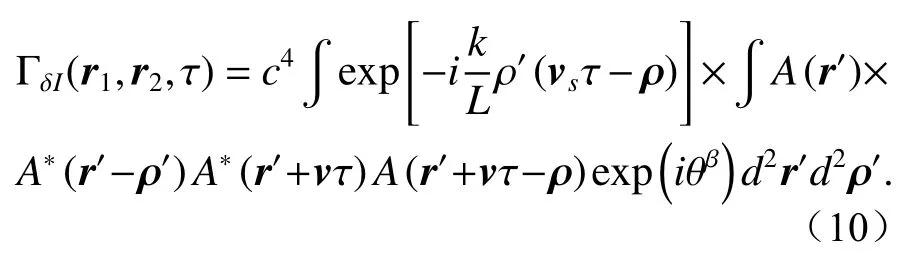
这里，

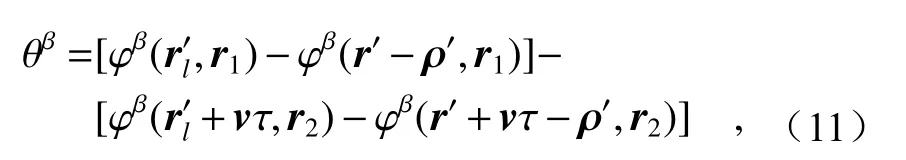
根据傅里叶变换的卷积定理可知，两个函数卷积的傅里叶变换等于两函数傅里叶变换的乘积。因此，公式（10）可化简为：

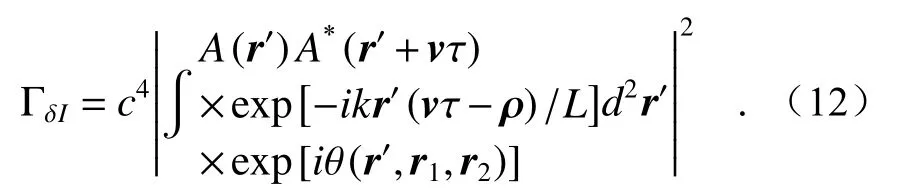
其中，θ(r', r1, r2) =φβ(r', r1)-φβ(r'+vτ, r2)是散射光从目标面(r',L)到探测面(r, 0)传输路径上穿过介质时引起的相位畸变差。传输介质简单分为两种情况：（a）当介质均匀时，θ(r', r1, r2)=0；（b）当介质非均匀而光学系统的目标是等平面时，相位畸变φβ相当于接收平面或者目标面前添加一个非常薄的相位屏。根据Vorontsov研究[26]可知，此时相位畸变函数φβ所产生的失真层对互相关函数没有明显影响。

因此，exp[ikr'vτ/L]可以用1替代。综上所述，散斑场波动的空间时间相关函数可化简为：

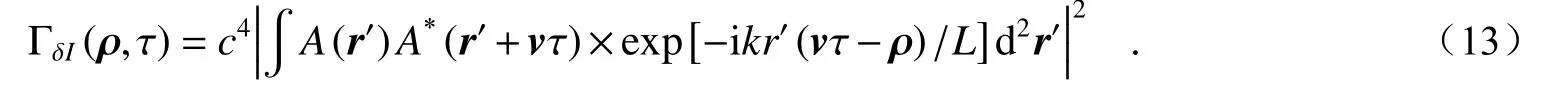
（1）散斑场光强波动的空间互相关函数：τ =0

I(r',L)为目标平面的光强分布，由此可看出散斑场强度的瞬时空间互相关函数是目标表面光强的傅立叶变换。通过获取回波散斑的MCF函数能够反映出目标表面处光斑的光强分布的变化。此外，探测面空间相关长度取决于函数I(r',L)的频谱宽度。假设目标表面处光斑的光强分布是空间坐标的高斯函数

其中bs表示目标面聚焦光斑的尺寸，Is为常量。将公式（15）代入到公式（14）中，可以得到探测面空间相关距离（即散斑大小）与目标光斑尺寸的关系

由此可见，目标面光强的互相关函数宽度能够估计动态散斑的大小，通过散斑尺寸可以反馈目标光斑的聚焦尺寸。

（2）散斑场光强波动的时间相关函数：ρ =0

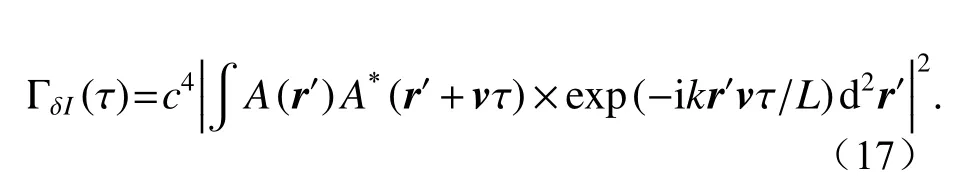
为了研究目标移动引起的散斑场强度的变化，需要保证A(r')A*(r'+vτ)项和exp(-ikr'vτ/L)是非零的。即满足两个时间尺度：τ＜τs，其中τs=bs/v，即目标面的坐标变化不得超过目标表面光斑尺寸；另一个尺度为τ0/τs＞ 1，其中τ0= L/(vkbs) =asp/v，即满足第一个时间尺度时，目标的散射元对应的相移量ikr'vτ/L很小，因此指数项exp[ikr'vτ/L]可以用1替代。

加入目标粗糙表面上满足高斯分布的激光公式（15）

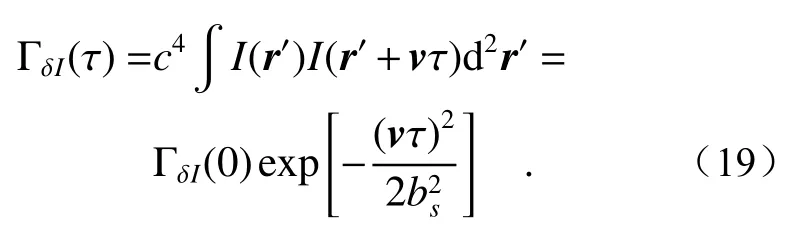
因此，散斑场的功率谱可以对散斑信号的相关函数做傅立叶变换得到

其中GδI为散斑信号的功率谱，ξI=v/bs为强度波动的特征频率带宽，其与目标上光斑尺寸呈反比例关系。综上所述，动态散斑的时间频谱带宽随目标聚焦光斑尺寸的增加而变窄。

2.2 探测面的不相关长度

为了解决单点探测短时间内获得足够数量样本难的问题，采用多通道同时探测，获得不同空间位点的散斑时间频谱信号。这种方法首先要保证的是，探测点获得的信号是不相关的。为了研究探测间距与回波散斑信号的相关性，需对照明光场A(r')的模数和相位进行完整的描述。以束腰宽度为ω0的基模高斯光束作为发射光束时，目标面光场A(r')可以表示为：

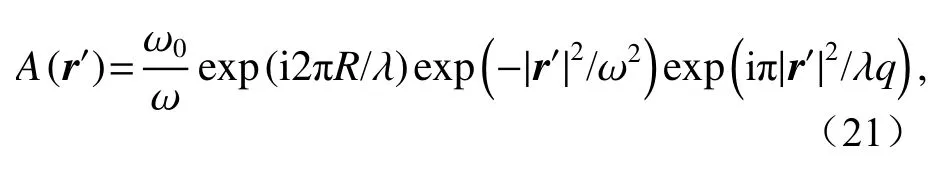
其中ω为激光光束的束宽和q为波面曲率半径，可由激光束腰位置到粗糙表面距离R表示

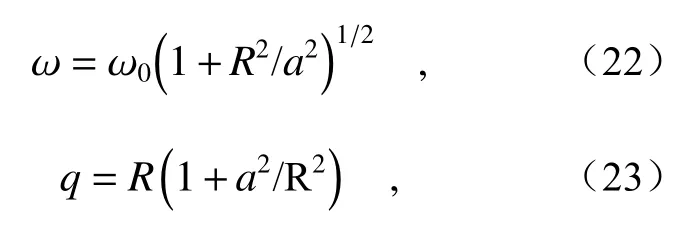
其中

带入散斑场的时间空间互相关归一化函数

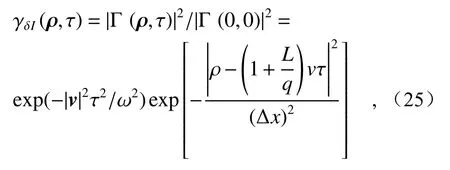
其中Δx=asp/2，表示回波散斑场中散斑的平均尺寸；L表示目标面到探测面的距离；z表示激光光束光腰到探测面的距离。将ρ=0带入公式（25），获得动态散斑强度波动的时间相关长度τc

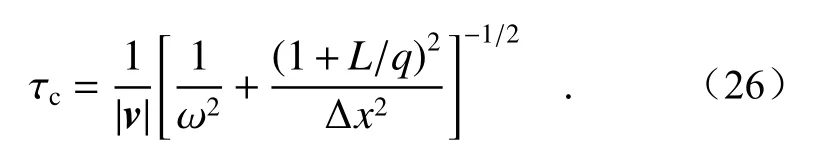
从方程（26）中可以看出，时间相关长度τc与粗糙目标移动速度的绝对值成反比，并且在高斯光束相关参数ω和q下，与散斑平均尺度存在紧密的关系[27]。带入到公式（25）可以得到

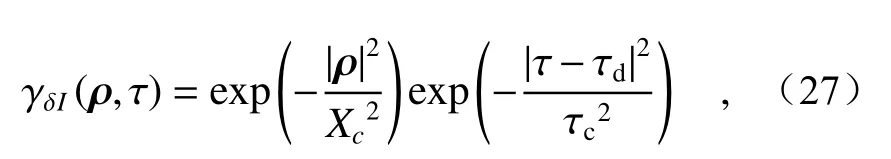
其中

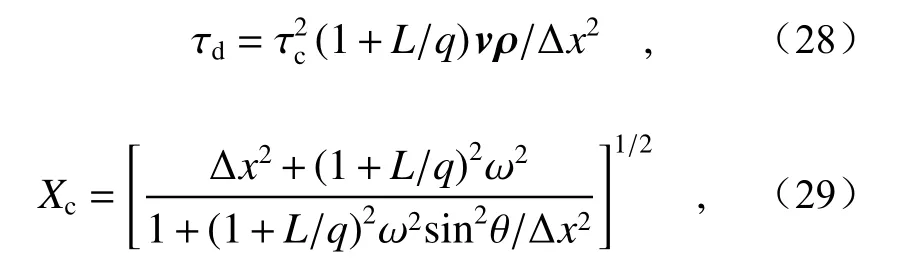
其中，τd为观察面(r1,t1)到(r2,t2)动态散斑强度的时间延迟，此时散斑场的时间空间互相关函数的相关峰位于τ=τd。当探测点间距ρ=Xc，相关峰的值为最大值的e-1。此时相关峰值达到极小值，十分微弱，信号可能会被噪声掩盖，这种条件下认为探测系统无法找到散斑强度波动的相关峰。认为两点采集的信号具有不相关性。其中θ表示粗糙目标运动方向和两探测点之间连线（向量v和ρ）的夹角。为了方便分析运算，假设探测点的摆放位置平行于粗糙目标速度矢量，且垂直于光轴。则公式（29）化简为

结合激光光束参数可以得到Xc

当探测间距ρ＞Xc，视为探测的信号去相关。

3 动态散斑仿真分析

动态散斑仿真过程较静态散斑更为复杂，为简化散斑图像的时间演化历程，建立一种散射点运动模型[28-29]，如图1所示。激光波长设为532 nm，10 m远放一匀速运动的目标靶面，目标表面粗糙均方根为30 nm, 相关长度为500 nm，且符合高斯随机分布。根据上述理论分析，探测器获得的散斑场光强波动信号为激光经目标面散射元漫反射后得到的光场相干叠加。这种模型不仅可以获得散斑场的统计特性，而且节约了大量的运算时间。

图1 散射点运动模型Fig.1 The model of the dynamic speckle

采用的光学系统布局如图2所示。单模激光通过准直扩束系统后，聚焦在以1 m/s匀速运动的目标靶面上，激光经粗糙表面漫反射后，经多通道单点探测器采集，探测平面与目标运动平面平行，单次采集2 000个数据。从而获得多通道的动态散斑强度随时间波动的信号。

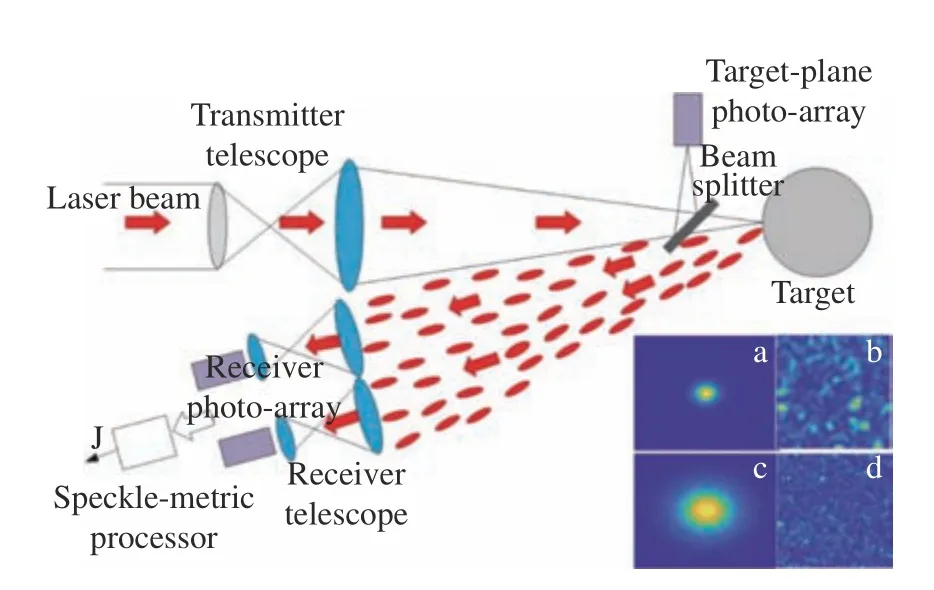
图2 TIL系统的光学布局图。出射激光复振幅A(r')通过均匀介质聚焦到目标靶面上，经粗糙表面散射后，回波由多个信号不相关的探测器接收。（a）目标粗糙表面直径为1.5 mm的聚焦光斑；（b）1.5 mm目标光斑对应的散斑光强；（c）目标粗糙表面直径为4 mm的聚焦光斑；（d）4 mm目标光斑对应的散斑光强。Fig.2 TIL wave propagation configurations.Transmitted wave with complex amplitude A(r') propagates in an optically homogeneous medium toward a target, and after scattering off the target surface at the plane (r',z=L), the return wave propagates back to the multichannel detectors.(a) Spot with a diameter of 1.5 mm focused on the target.(b) The speckle pattern corresponds to (a).(c) Spot with a diameter of 4 mm focused on the target, and (d) shows the speckle pattern corresponding to (c).

为了研究探测点间距与散斑信号的相关性，光斑半径设为ω0= 4 mm，采集信号的两点间距由3 mm调整到6 mm，对获得的散斑强度随时间波动的信号做互相关。仿真结果如图3所示，探测间距小于公式（31）计算的最大相关距离时，回波信号具有明显的相关峰；探测间距大于最大相关距离时，两个信号可以在相关峰处明显分辨，表现出了去相关性[30]。因此证明，探测面多通道的探测点间距远大于最大相关距离时，可以认为多通道同时获得的散斑信号在时间上是不相关的，也就是获得的散斑频谱在统计学上是独立的。

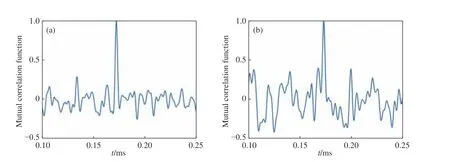
图3 动态散斑强度波动归一化互相关函数仿真结果。（a）ρ=3 m；（b）ρ=6 mFig.3 The simulation results of the dynamic speckles normalized cross-correlation function.(a) ρ=3 m; (b) ρ=6 m

根据散射点运动模型获得的探测面某点散斑强度随时间变化的波动信号的仿真结果如图4（a）所示，对信号进行自相关运算和傅立叶变换得到时间频谱，图4（b）（彩图见期刊电子版）立体展示了散斑时间频谱带宽与目标光斑尺寸的关系。聚焦光斑直径由1.2 mm变为0.2 mm。随着聚焦效果逐渐增加，散斑场的时间频谱带宽明显增大。仿真结果与理论分析结果相吻合。由此可见，可以从动态散斑频谱带宽中获得的评价因子反馈目标光斑的聚焦效果。

图4 根据点运动模型探测的动态散斑信号。（a）探测面一定孔径内的散斑强度波动信号；(b)目标光斑半径由0.2 mm逐步变为1.2 mm时，对应的散斑功率谱带宽逐渐缩短。Fig.4 The dynamic speckle signals according to the model of the movement of Scatters.(a) Speckle signal fluctuations.(b)The frequency bandwidth of the power spectra decreases as the target spot size changes from 0.2 mm to 1.2 mm

由于动态散斑强度波动信号在有限的采样时间内获得的频谱输出结果会存在估计误差。根据Akhmanov等人[31]对频谱误差的研究分析可知，这一误差主要取决于频谱GI的分布形态和采样时间。为减小误差，首先要求采样时间尽可能延长，T≫1/ωI（其中ωI为频谱带宽的截止频率），即v≫bs/T。其次输出值误差的方差逐渐逼近GI(ω=0)/T，这表明误差主要来自于低频频谱分量上的波动，因此，为了减小误差，需要降低低频贡献。通过对频谱图乘以逐步增大的权重积分求和的方式降低低频贡献，获取散斑评价因子J：

其中βi= 1/(n-i)为权重参数，随着光谱区域的中心频率的增大而增大。Δ为通过频谱图将输出结果等分成n份的光谱区域，每个光谱带的宽度。ωi为每个光谱区域所对应的中心频率。散斑因子J的探测精度主要取决于权重参数βi。对比单通道获取的动态散斑时间频谱，N通道同时采集可以联合散斑的空间时间统计特性对目标光斑能量进行判断。对空间不相关的时间频谱获得的结果取平均，可以假设误差εT是随机和独立的，重复独立测量K次，则理论上这种取平均获得的评价因子测量精度将比单通道提高倍。

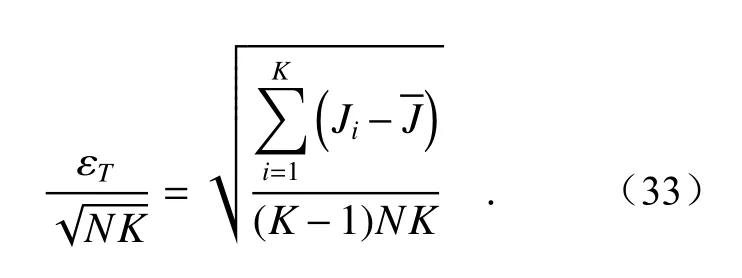
另一种方法，在每次采集足够的信号前提下，对多通道散斑波动信号截断1/N后连接信号获取散斑频谱，将空间与时间统计特性同时融入到回波评价体系中，可以视为在牺牲探测像素的前提下扩大探测空间口径，以提高散射光场对远场上光斑质量评价的精度与效率。

根据上述参数设置，在探测面选取两两间隔50 mm的4个空间位点，4个单点探测器单次采集2 000个数据，采集100次独立且随机的结果取平均，获得的归一化评价因子J仿真结果如图5（彩图见期刊电子版）所示。其中蓝色曲线为单通道获得的评价因子Jone，红色曲线对应4个通道结果取平均的评价因子Jave，黄色曲线为多通道信号截断获得时间空间频谱得到的评价因子Jspt。通过对比仿真结果，可以看出动态散斑时间频谱获得的评价因子会随目标光斑聚焦尺寸增加而逐渐减小，符合动态散斑时间频谱获得评价因子的理论分析。且评价因子Jave的曲线比单通道的Jone平滑，这验证了对空间不相关散斑信号结果取平均的精度会有明显提高；评价因子Jspt结合了散斑场时间空间信息，获得数值明显高于利用散斑时间频谱获得的评价因子，曲线不仅趋势与单通道的一样，而且下降更为明显。

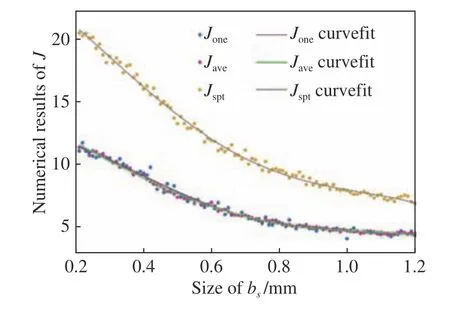
图5 评价因子随目标光斑尺寸变化的仿真结果。目标光斑半径从0.2 mm变为1.2 mm，间隔为0.01 mmFig.5 Simulation results of the speckle-metric varying with the target spot size from 0.2 mm to 1.2 mm,with an interval of 0.01 mm

为使结果更清晰，在图5中拟合了评价因子的4次多项式拟合曲线，对比残差值分析对应评价因子的精度。表1显示了基本拟合信息，相关系数R2和误差估计RMSE。相关系数大于0.9认为拟合曲线是正确的。误差估计的结果证实了4通道获得的Jave精度将比单通道Jone提高接近2倍，而Jspt精度略低与单通道Jone精度，但是结合时间空间信息的这种方法在获得相同采样量时，速度会提高4倍。综上所述，多点协同获得的散斑评价因子反馈目标光斑尺寸信息的方法是可行的，且评价因子的精度和效率均有所提高。

值得注意的是，评价因子Jspt数值大于单通道的，这是因为在信号拼接过程中出现了一定的谐波。这种情况会在数据少量时更为明显，以单通道采集400个数据而4通道单次采集100个数据叠加为例，对比获得的散斑时间频谱如图6（a）（彩图见期刊电子版）所示，可以看出拼接散斑光强波动的方法在数据量较少时，会使频谱出现高度突变，类似于谐波。为研究这种情况是否对评价因子的准确性造成影响，4个通道单独采集100、200、500组数据，分析50次独立探测取平均的评价因子Jspt随目标光斑的尺寸变化结果如图6（b）（彩图见期刊电子版）所示，归一化结果显示，单次采样数据量充足时，频谱谐波不影响评价因子的准确度。

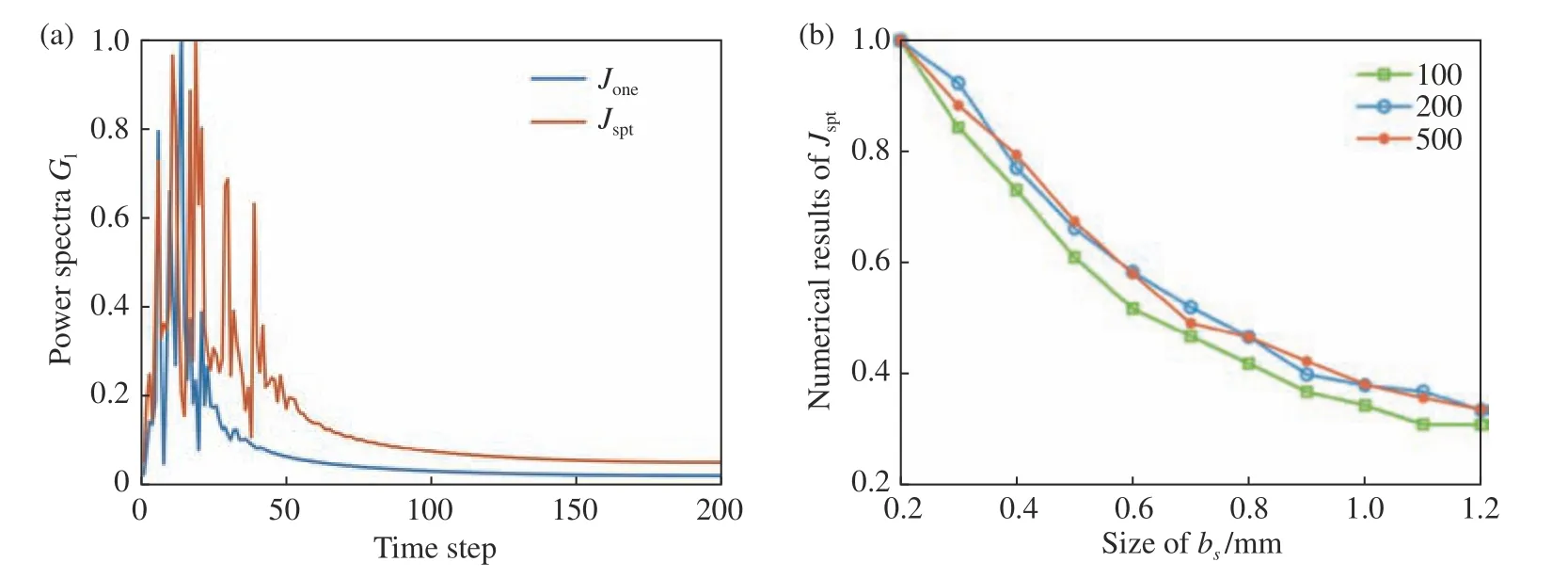
图6 （a）单通道获得的时间频谱和4通道获得的时间空间频谱。（b）四通道获得的归一化评价因子随目标光斑尺寸的变化Fig.6 (a) Temporal spectrum obtained by a single-channel, and the spatio-temporal spectrum obtained by a four-channel.(b)The normalized speckle-metric obtained by the four-channel varying with the target spot size

表1 拟合信息Tab.1 Fitting results

4 实验结果

搭建由两个单点探测器采集激光回波散斑的实验平台，如图7所示，激光经准直扩束和聚焦系统汇聚到旋转的粗糙目标靶面上，光束质量分析仪探测目标聚焦光斑的共轭面获得光斑的尺寸信息，携带着靶面信息的激光回波由两个焦距为10 cm的透镜汇聚到探测面，经两个Thorlabs单点探测器接收。实验测量的目标光斑半径为：0.403 3、0.498 8、0.697 1、0.935 7、1.060到1.233 mm。双通道结构可以通过后向散射增强效应提高接收信号的信噪比。激光光源的波长为532 nm，通过聚焦系统将光束会聚到7.5 m远的漫反射目标圆盘上，转动线速度为1.256 m/s，经漫反射产生的动态散斑场由两个相同的回波接收系统汇聚到激光光源旁的单点探测器内，两个探测器间隔10 cm且摆放位置和目标运动方向平行，采样率均为1 MHz，每组采集106组数据。经计算，目标的截止频率为6 280 Hz，满足探测条件。实验中可以通过调整发射端聚焦系统的焦距，改变目标靶面的聚焦光斑尺寸，并利用分光镜获得目标光斑的共轭面，通过光束质量分析仪无接触探测其艾里斑半径。对探测器接收的散斑强度波动信号进行滤波、自相关和傅立叶变换，分析通过时间频谱信号获得的评价因子与目标光斑尺寸之间的关系。

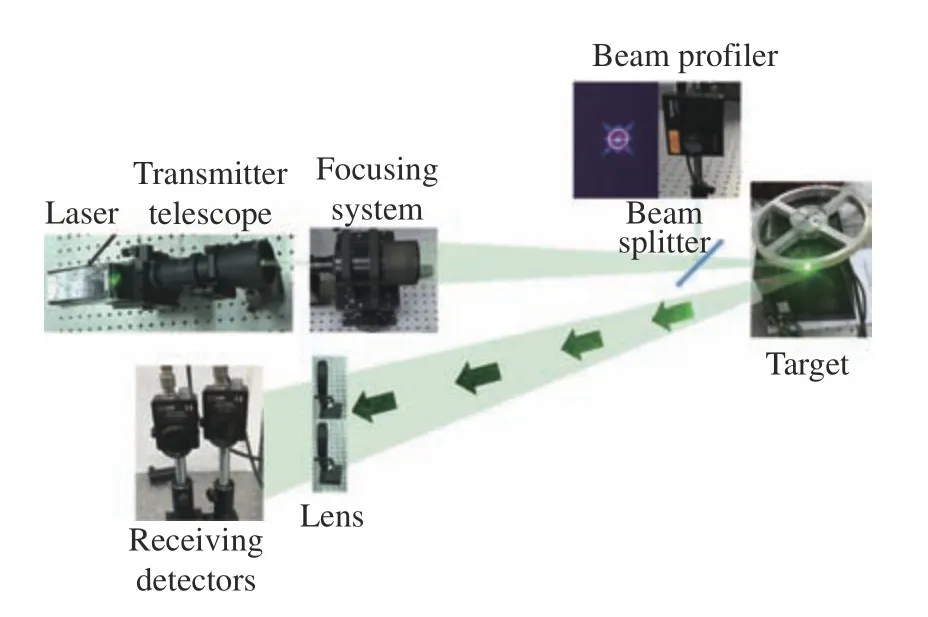
图7 两个单点探测器采集激光回波散斑的实验平台Fig.7 Experimental platform for collecting laser echo speckle with two single-point detectors

实验中通过动态散斑时间频谱获得评价因子实验结果如图 8（彩图见期刊电子版）所示，图 8（a）和 8（b）为两个单点探测器分别获得的时间频谱，x轴代表频率，y轴代表目标面激光光斑尺寸，z轴代表实验中获得的散斑波动信号功率谱。散斑强度波动功率谱的结果曲线颜色分别为红、黄、绿、蓝、靛、紫，依次代表对应目标光斑尺寸为12.33 mm、10.6 mm、9.357 mm、6.971 mm、4.988 mm、4.033 mm。（c）为两个单点探测器经10次独立测量取平均获得的两组单通道评价因子Jone，图8(d)对应两通道的实验结果取平均获得评价因子Jave和融合空间时间频谱的评价因子Jspt。可以看到通过权重获得的评价因子能够更直观地反映出目标光斑的变化，提高了频谱法监视光斑的精度，同时实验验证了动态散斑的时间频谱带宽会随目标光斑尺寸的增加而减小。此外，图8（c）单通道评价因子的结果在光斑尺寸为0.935 7 mm处存在一跳点，这是因为评价因子是根据散斑的时间统计特性获得的，存在概率及光束抖动问题。图8（d）的实验结果证实了多通道探测的方法可以提高探测精度，和结合空间时间两个维度的方法获得的评价因子可以反馈目标光斑尺寸信息，并且使系统的带宽提高两倍。

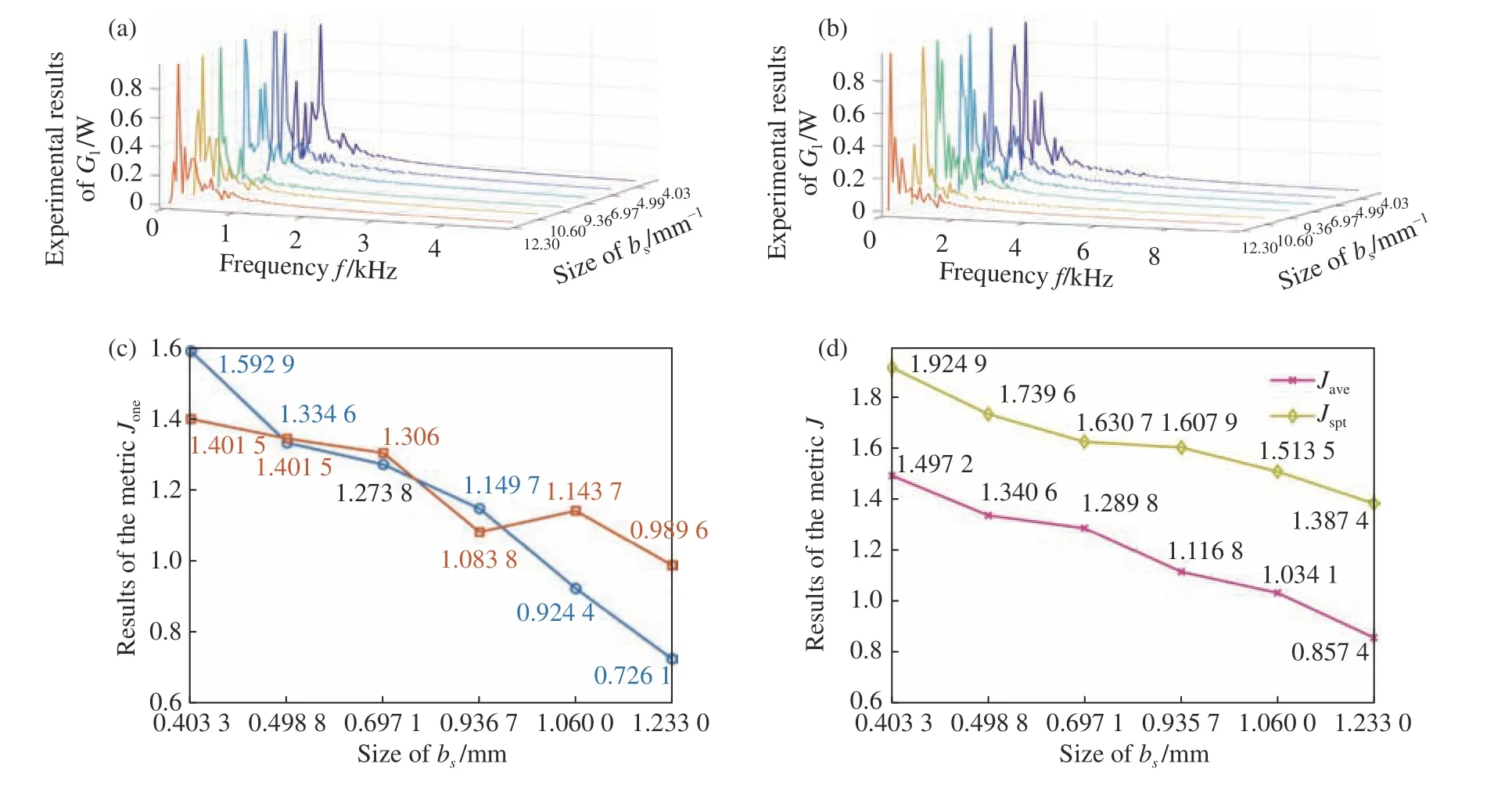
图8 散斑强度频谱法实验结果，（a）和（b）中横坐标表示强度波动的频率，纵坐标为两个探测器获得的归一化时间频谱。（c）两个单点探测器获得的评价因子Jone实验结果，（d）对应两通道的实验结果取平均获得评价因子Jave和融合空间时间频谱的评价因子Jspt.Fig.8 Experimental results of the speckle spectroscopy method.The horizontal coordinates in (a) and (b) indicate the frequency of intensity fluctuations, and the vertical coordinates are the normalized temporal spectra obtained from the two detectors.(c) Results of the speckle-metric Jone obtained by two point detectors, and (d) shows the speckle-metrics obtained by averaging the two-channel results (Jave) and the spatial-temporal spectrum (Jspt).

5 结 论

本文提出了一种多点协同探测获取动态散斑评价因子的方法，在充分利用单点探测器高采样速率前提下增加了空间维度，为解决应用散斑统计特性探测目标信息过程中系统带宽小、采样时间长等问题提供了新的思路。4通道协同采集散斑信号，对时间频谱的仿真结果取平均获得的评价因子Jave测量精度比单通道提高了2.05倍；而融合时间空间频谱取平均获得的评价因子Jspt仿真结果表明，这种以牺牲像素为代价，扩大探测孔径的方法在保证精度同时可以使系统带宽提高4倍。此外，实验验证了理论与仿真的正确性，两种方法获得的散斑评价因子可以监视毫米量级目标的尺寸变化，且多点协同探测方法可以提高散斑评价因子监视远场目标光斑系统的精度和带宽。本文将为利用动态散斑评价因子实现闭环实时光束校正的工程应用提供理论依据和数据支撑。